Linking CGE and microsimulation models: A comparison of different approaches

Cite this article as: G. Colombo; 2018; Linking CGE and microsimulation models: A comparison of different approaches; International Journal of Microsimulation; 3(1); 72-91. doi: 10.34196/ijm.00026

Article
Figures and data
Jump to

Abstract

In the literature that studies income inequality and poverty, a recent development has been the development of models that link together a macroeconomic model (usually a Computable General Equilibrium (CGE) model) and a microsimulation model. Linking the two types of model allows the modeller to take into account full agents’ heterogeneity, whilst at the same time considering the general equilibrium effects of a proposed policy reform. In this paper, I first review in detail three approaches to building linked CGE-microsimulation models: one in accordance with the fully integrated approach, and two following the layered approach (the so-called Top-Down and Top-Down/Bottom-Up approaches). The principal goal of the paper is to present a considered evaluation of the merits and demerits of these alternative methods currently used to link CGE and microsimulation models. To do so I use all three approaches to model the macro- and micro-economic impacts of a policy shock to an archetypical economy (constructed using fictitious data), and compare the results. This analysis highlights the importance of (i) consistency between the underlying macro- and micro-data; and (ii) the precise mechanisms by which feedback effects are passed between the macro and micro models. I develop this latter point further by detailed analysis of the TD/BU approach outlined by Savard (2003), leading to a proposed refinement in the way that feedback effects from the micro level of analysis are incorporated back into the CGE model.

1. Introduction

The study of poverty and inequality in developing countries usually requires two main focuses: on one side a microeconomic focus is required to have a detailed and precise picture of incomes and/or expenditures at the individual and household level, and to model individual and household behavioural responses to some reforms/shocks, with a special concern for those whose income is around the poverty line; on the other side, a macroeconomic focus is often needed, as most of the economic policies (structural adjustment programs or trade liberalizations, for example) and of the exogenous shocks commonly analyzed for developing countries (such as fluctuations in the world price of raw materials and agricultural exports) are often macroeconomic phenomena (or may have, at least, some structural effects on the economy).

Since the pioneering work by Adelman and Robinson (1978) for South Korea and Lysy and Taylor (1980) for Brazil, many Computable General Equilibrium (CGE) models for developing countries combine a highly disaggregated representation of the economy within a consistent macroeconomic framework and a description of the distribution of income through a small number of representative households (RHs). In order to account for heterogeneity among the main sources of the changes in household income, several “representative households” are necessary. Despite this need for variety, the number of RHs is generally small in these models (usually less than 10).

The CGE/RH framework sometimes explicitly considers that households within a RH group are heterogeneous in a “constant” way. That is, in order to capture within-group inequality, it is assumed that the distribution of relative income within each RH follows an exogenous statistical law¹. But the assumption that relative incomes are constant within household groups is not reflected in reality. Indeed, empirical analyses conducted on household surveys show that the within-group component of observed changes in income distribution is generally at least as important as the between-group component of these changes². Thus, the RH approach based on this assumption may be misleading in several circumstances, and this is especially true when studying poverty. This argument may be better understood by presenting an example: consider a shock on the world market of a certain good, which leads to a decrease in the exports and to a domestic contraction of this sector in the specific exporting country under study. After the simulation of the shock with a CGE/RH model, suppose that I find a little change in the mean income of a particular RH group, say workers in the agricultural sector. In this case, poverty might be increasing by much more than suggested by this drop in income: indeed, in some households there may be individuals that lose their job after the shock, or that encounter more difficulties in diversifying their activity or consumption than others. For these individuals or families, the relative fall in income is necessarily larger than for the whole group, and this fall in their income is not represented by the slight fall in the mean income of the whole group. Suppose, moreover, that the initial income of these individual was low. Then poverty may be increasing by much more than what predicted by a simple RH model, which is based on the assumption of distribution neutral shocks. So, the RH approach does not capture the effects that a shock or a policy change may have on single individuals or households within a RH group.

In contrast, microsimulation models can be very precise and detailed in their representation of microeconomic individual behaviour, but necessarily miss an important part of the story since they involve only a partial equilibrium analysis. In short, they miss a very important aspect represented by general equilibrium models which is the structural effects of the reform/shock under study.

In order to overcome these problems, the recent literature has tried to develop new modelling tools which should be able at the same time to account for heterogeneity and for the possible general equilibrium effects of the policy reform (or the exogenous shock) under study. In view of the fact that most of the available economic models have either a microeconomic or a macroeconomic focus, and hence do not address the question adequately, the recent literature has focused on the possibility of combining two different types of models. In particular, some authors have tried to link microsimulation models to CGE models, in order to account simultaneously for structural changes, for general equilibrium effects of the economic policies, and for their impacts on households’ welfare, income distribution and poverty. (More generally, this current of the literature develops the use of micro-data drawn from household surveys in the context of a general equilibrium setting, which is usually but not necessarily a CGE model.) The literature that follows this approach has flourished in recent years: there are, among others, the important contributions by Decaluwé et al. (1999a) and (1999b), Cogneau and Robilliard (2001, 2004 and 2006), Cockburn (2001), Cogneau (2001), Bourguignon et al. (2003b), Boccanfuso et al. (2003), Savard (2003) and Davies (2009).

In this paper I have two main aims. First, to summarise recent developments in this field by detailing the three main methods developed to link the micro-data from a survey into a CGE model: the full integration of survey data into a CGE framework, as is done for instance in Cockburn (2001); the linking of a behavioural microsimulation model to a CGE through a set of specific equations as developed in Bourguignon et al. (2003b) – the so called Top-Down method; and the iterative coupling of CGE and microsimulation outputs as developed by Savard (2003) – the Top-Down/Bottom-Up model. Second, to present an assessment of the relative strengths and weaknesses of each of these three approaches.

To fulfil these aims, in this paper I first outline each approach to linking CGE and microsimulation models in detail (Sections 2 to 4). I then use all three approaches to simulate the impact of an identical policy reform, using as inputs for each the same data from a fictitious economy. The use of fictitious data describing a simple economy permits better understanding of the differences that are observed in the results of the models, and of the causes that generate them. Having constructed and run the models, in Section 5 I compare and contrast the macro- and microeconomic outcomes derived from each type of model linking, drawing lessons regarding the importance of data consistency and feedback mechanism. This leads on to a more detailed analysis of the TD/BU approach as developed by Savard (2003), and the proposal of an alternative way of taking into account feedback effects from the micro level of analysis into the CGE model.

2. The integrated approach

The first approach to linking CGE and microsimulation models that I will consider is the ‘integrated’ approach. The main intuition behind this approach is to substitute the Representative Household Groups inside a standard CGE model with the real households that are found in the survey. The first attempt in this direction was made by Decaluwé et al. (1999b). Among the models following this approach there are the works by Cockburn (2001) for Nepal, by Boccanfuso et al. (2003) for Senegal, and by Cororaton and Cockburn (2005), who studied the case of the Philippine economy.

In practice, under this approach, one passes from a model with, for instance, ten representative agents to a model with thousands of agents, thus increasing the computational effort, but leaving substantially unchanged the modelling hypothesis of a standard CGE model. Basically this approach does not include a true microsimulation module in the modelling framework, but tries to incorporate the data from the household survey into the CGE model.

The first step in building such a model is to pass from the representative households’ data to population values; to do this, one should weight each variable at the household level with the weights given in the survey, thus obtaining population values for each variable. After this, a procedure is required to reconcile these population data coming from the survey (incomes and expenditures) with the accounts contained in the social accounting matrix (SAM). (For a fuller account of the SAM, see Section 3.2.) The literature on data reconciliation offers different alternatives. One may choose to keep fixed the structure of the SAM and adjust the household survey, or to adjust the SAM in order to meet the totals of the household survey. Intermediate approaches are also possible. Whatever the method used, however, one necessarily loses the structure of the original data, which is one of the main drawbacks of the integrated approach. For this paper I have chosen the first alternative, and kept the original composition of households’ incomes and expenditures unchanged.

After these changes in the SAM, one encounters the problem of re-balancing it (row totals must be equal to column totals). To do this, I used an appropriate program that minimizes least squares³.

The CGE model I use for application of the integrated approach is the one described in Section 3.2, except for the addition of an index which refers to households. This way, for instance, the consumption demand function in Table 8 becomes:

P_{q} . C_{m q} = α H_{m q} . C B U D_{m},

where m is now the index for households.

One thing should be noted at this point: certain types of equations that are commonly included in a behavioural model, such as occupational choice equations, are not easily modelled within standard CGE modelling software (see Savard, 2003), so that CGE-MS models that follow the fully integrated approach are not always able to capture the behavioural responses of the agents to the policy reforms that are implemented. Instead, micro-econometric behavioural modelling provides much more flexibility in terms of the modelling structure used, and is more suitable to describe the complexity of household and individual behaviour, and the way this may be affected by the changes in the macroeconomic framework that are subsequent to a policy reform or an external shock.

The main point here is that with a CGE model like the one used for the integrated approach I am not able to predict which particular individual will enjoy the reduction (or will suffer from the rise) in the employment level on the basis of some characteristics of the individual or of the household that can be observed; this instead can be done through a behavioural microsimulation model.

Indeed, the main feature that differentiates a microsimulation model from a standard CGE framework (not only one with representative agents, but even one with thousands of households from a survey, as we have seen) is that it works at the individual level, selecting those individuals, on the basis of their personal or family characteristics, that show the highest probability of changing their labour market status. This fact could bring about significant differences in the results between the two types of models, even after the same policy simulation, as we will see below.

3. The top-down approach

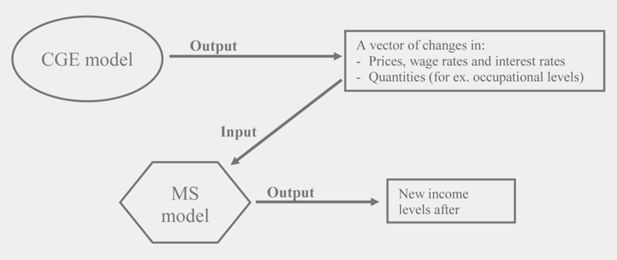
I now turn to the sequential or Top-Down approach described in Bourguignon et al. (2003b). The basic idea here is to develop a stand-alone microsimulation (MS) model, and then to run it taking account of changes in consumer/producer prices, wages, and sectoral employment levels predicted by a CGE model. This approach thus uses the two frameworks in a sequential way: first, the policy reform is simulated with the CGE model, then simulated changes in selected variables, such as prices, wage rates, and employment levels, are passed down to the MS model, as illustrated in Figure 1.

Figure 1

Download asset Open asset

When the assumption of imperfect labour market is adopted, or when the presence of a formal and an informal sector is predicted, the rationing in the labour market is usually carried out in the macro or CGE model, while the main use of the MS module is to select those households or individuals who will actually be barred out of, or let in, employment, or the formal sector. We will see this in more detail in Section 5, when the simulation results are presented.

3.1 The microsimulation module

The main role of the microsimulation module in the linked CGE-MS framework is to provide a detailed computation of net incomes at the household level, through a detailed description of the tax-benefit system of the economy, and to estimate individual behavioural responses to a policy change. For instance, through the use of microeconometric equations, we can model behaviours such as labour supply or consumption.

Behavioural Microsimulation (MS) models are developed to capture the possible reactions of the agents to the simulated policies, so that what happens after a reform can be very different from what is predicted by the simple arithmetical computations included in an accounting model.

In this section I will describe in detail a simple behavioural model, following quite closely the discrete labour supply choice model used in Bourguignon et al. (2003b). Another description of a similar MS model for labour supply can be found in Bussolo and Lay (2003) with their model for Colombia, and in Hérault (2005), who built a model for the South African economy.

For the building of the model I will use fictitious data describing a very simple economy. In the household survey I have information about some individual characteristics, such as age, sex, level of qualification, education, labour and capital income, the eventual receipt of public transfers, and the activity status. For the sake of simplicity, I have stated that each individual at working age (16-64) can choose between only two alternatives: being a full-time wage worker, or being unoccupied. There are other variables in the survey that refer to households rather than to individuals, for example the area of residence, the number of adults (over 18 years old) and children (under 18), and so on. Also for the sake of simplification, I have grouped all consumption goods within the economy into two main categories.

The focus of my distribution and poverty analysis will be on disposable income, even if in principle an inequality and poverty analysis could also be conducted on expenditure rather than on income levels.

I derive income variables referring to households from initial individual data by summing up individual values for each household member; this way, I obtain households’ labour and capital incomes, households’ public transfers and households’ total income, respectively:

Y L_{m} = \sum_{i = 1}^{N C_{m}} Y L_{m i}

Y K_{m} = \sum_{i = 1}^{N C_{m}} Y K_{m i}

T F_{m} = \sum_{i = 1}^{N C_{m}} T F_{m i}

Y_{m} = Y L_{m} + Y K_{m} + T F_{m},

where YL_mi is labour income of individual i member of household m, YK_mi his/her capital income, and TF_mi are the public transfers he/she receives from government. All these quantities are summed up for each family over all the individuals belonging to the family (NC_m is the number of components of household m); then, household m’s total income, Y_m, is the sum of all incomes received by the family: labour income, capital income, and public transfers.

For the benchmark situation, I assume all initial prices normalized at one.

3.1.1 The model

The core of the behavioural model is represented by the following two equations:

L o g (Y L_{m i}) = a + b \cdot X_{m i} + c \cdot Λ_{m i} + v_{m i}

W_{m i} = I n d [α + β \cdot Z_{m i} + γ \cdot R W_{m i} + ε_{m i} > 0]

The first equation is a regression model for logwage earnings, while the second one represents individuals’ “choice” for labour market status (see below for further explanations).

The rest of the MS module comprises simple arithmetical computations of price indices, incomes, savings and consumption levels. As the parameters entering the following equations (marginal propensity to save mps_m, income tax rates γ, and budget shares η_mq) are constant, this part of the model may be regarded as purely accounting, as it does not contain any possible behavioural response to policy simulations.

Household m’s income generation model:

Y_{m} = \sum_{i = 1}^{N C_{m}} Y L_{m i} \cdot W_{m i} + Y K_{m} + T F_{m}

Household disposable (after tax) income:

Y D_{m} = (1 - γ) \cdot Y_{m}

Household specific consumer price index:

C P I_{m} = \sum_{q = 1}^{2} η_{m q} \cdot P_{q}

Real disposable income:

Y D R_{m} = Y D_{m} / C P I_{m}

Savings:

S_{m} = m p s_{m} \cdot Y D_{m}

Household consumption budget:

C E B U D_{m} = Y D_{m} - S_{m}

Consumption expenditure for commodity q:

C E_{m q} = η_{m q} \cdot C E B U D_{m}

Consumption level of commodity q:

C_{m q} = \frac{C E_{m q}}{P_{q}}

Household m’s capital income:

Y K_{m} = P K \cdot K S_{m}

See Table 1 for a description of the subscripts.

Table 1

Description of the subscripts for the microsimulation model.

m	Households	m = 1, 2, …, 24
i	Individuals belonging to household m	i = 1, …, NC_m	(NC_m: number of components of household m)
q	Goods	q = 1,2

The first equation of the model, (6), computes the logarithm of labour income (wage) of member i of household m as a linear function of his/her personal characteristics (vector X_mi includes the logarithm of age, sex, skill level and educational attainment) and of Λ_mi, which represents the inverse Mills ratio estimated for the selection model (for more details on the estimation process see below). The residual term v_mi describes the effects of unobserved components on wage earnings.

The second Equation (7) represents the choice of the labour status made by household members. In the literature this kind of equation is known as an occupational choice model, or selection model (and also discrete choice model of labour supply). However, it must be specified that in our case this equation is not really intended to explain the individual choice between being occupied or unemployed, but rather it tries to find out which characteristics strengthen the probability of being in one condition rather than in the other one for each individual, as described in more detail in the estimation section below.

Each individual at working age has to choose between two alternatives: being a wage worker, or being inactive. The variable W_mi is a dichotomous variable taking value one if individual i of household m is a wage worker, and zero otherwise. The choice is made by each individual according to some criterion, the value of which is specific to the alternative, and the alternative with the highest criterion value is selected. A natural economic interpretation of this criterion value is utility: each individual chooses the alternative with the highest associated utility. I will estimate this selection model using a binomial logit specification, which assigns each individual to the alternative with the highest associated probability. In the model I have arbitrarily set to zero the utility of being inactive. Function “Ind” is an indicator function taking value one if the condition is verified, and zero otherwise. Vector Z_mi of explanatory variables includes some personal characteristics of individual i of household m, that is: age, sex, skill and educational level, the area of residence and the number of children under 6 living in the household. Variable RW_mi is the logarithm of real labour income. The equation is defined only for individuals at working age.

Equation (8) is an accounting identity that defines total household income, Y_m, as the sum of the wage income of its members YL_mi, of the exogenous household capital income YK_m, and of the total amount of public transfers received by household m, TF_m. In this equation, variable W_mi stands for a dummy variable that takes value one if member i is a wage worker and zero otherwise.

Equation (9) computes household disposable (after tax) income by applying income tax rates according to the rule reported in Table 2. In order to simplify computations, I have assumed that in this economy direct income taxes are imposed on households’ total income Y_m, and not on individual incomes.

Table 2

Direct income tax rates.

Household Income	Tax rate
Up to 10,000	0%
Up to 15,000	15%
Up to 26,000	24%
Up to 70,000	32%
Over 70,000	39%

The fifth equation computes a household-specific consumer price index through the consumption shares η_mq. Real disposable income is then obtained by dividing each household’s disposable income by this index (Equation (11)).

To find a household m’s savings level, equation (12) multiplies this disposable income by the marginal propensity to save of each household, mps_m. The assumption underlying this equation is that household savings behaviour is unvarying, as the savings level is a fixed fraction of household disposable income. Then, subtracting savings from disposable income one obtains the budget that each household spends on consumption (Equation (13)), which is spent on of the two goods in the model according to the budget shares η_mq, using equation (14). Again, the assumption underpinning this equation is that consumption behaviour is not flexible: that is, households spend a constant fraction of their consumption budget for each of the two goods.

To get the values of these exogenous parameters (marginal propensity to save mps_m and budget shares η_mq), I use the initial data from the survey in the following way:

m p s_{m} = \frac{S_{m}}{Y D_{m}}

η_{m q} = \frac{C E_{m q}}{C E B U D_{m}} .

Equation (15) then derives the consumption levels for each household by dividing the expenditure for each good by its price.

Finally, income from capital is obtained by multiplying capital endowment of each family, KS_m, by the return to capital, PK (Equation (16)).

The initial values of the variables C_mq and KS_m (consumption levels and capital endowments, respectively) are derived from the survey data making use of the assumption that in the benchmark situation all prices and returns are equal to one:

C_{m q} = C E_{m q}

K S_{m} = Y K_{m}

Moreover, I assume that public transfers paid to households and household capital endowments are exogenously given. They are fixed at the level reported in the survey, for public transfers, and at the level as computed in Equation (20), for capital endowment, respectively.

3.1.2 Estimation of the model

The only two equations in the MS module that need to be estimated are Equations (6) and (7). The former, which expresses the logarithm of wage earnings as a linear function of some individual characteristics and of ∧_mi, the inverse Mills ratio, was estimated using a Heckman two-step model (see Heckman (1976) and (1979)). I followed this approach to correct for the selection bias which is implicit in a wage regression, that is, the fact that I observe a positive wage only for those individuals that are actually employed at the moment of the survey.

The results of the estimation are reported in Table 3. The estimation was conducted on the subsample of individuals at working age (16–64). The aim of the wage equation in the model is to assign an estimated wage to the individuals that are inactive in the survey, and change their labour market status after the simulation run.

Table 3

Heckman selection model, two-step estimates.

	Coefficient	Std. Error	z	P>\|z\|
constant	7.0321	0.3145	22.36	0.000
ln(age)	0.6978	0.0833	8.38	0.000
sex	−0.4662	0.1018	−4.58	0.000
qualification	0.3966	0.0772	5.14	0.000
education	0.5250	0.0872	6.02	0.000
Mills ratio	0.2160	0.1473	1.47	0.143
Selection
ln(age)	0.3386	0.0807	4.19	0.000
sex	−1.5492	0.2803	−5.53	0.000
qualification	1.0204	0.2729	3.74	0.000
children under 6	0.1682	0.2368	0.71	0.478
region	−0.7515	0.2980	−2.52	0.012
rho	0.7628
sigma	0.2832

Notes: Dependent variable: logarithm of wage.

Parameters of Equation (7) were obtained through the Maximum Likelihood estimation using a binomial logit model and assuming that the residual terms ε_i, are distributed according to the Extreme Value Distribution – Type I⁴. The estimation was conducted on the sub-sample of individuals at working age (16–64). Explanatory variables include individual characteristics such as the logarithm of predicted real wage, sex, skill and education level, as well as the region of residence and a variable accounting for the presence or not of children under 6 years old in the household. Results are presented in Table 4.

Table 4

Binary logit model of labour status choice.

	Coefficient	Std. Error	z	P>\|z\|
ln(real wage)	0.1972	0.0465	4.25	0.000
sex	−1.8948	0.4078	−4.65	0.000
qualification	1.4408	0.4257	3.38	0.001
region	−0.7185	0.3295	−2.18	0.029
children under 6	0.2691	0.2973	0.91	0.365
education	−0.7633	0.6717	−1.14	0.256
Mean dependent var	0.6647	S.D. dependent var		0.4735
S.E. of regression	0.3767	Akaike info criterion		0.9015
Sum squared resid	23.2688	Schwarz criterion		1.0122
Log likelihood	−70.6305	Hannan-Quinn criter.		0.9464
Avg. log likelihood	−0.4155

Notes: Dependent Variable: Activity Status.

With the estimated coefficients I cannot perfectly predict the true labour market statuses that are actually observed in the survey. Thus, following the procedure described in Duncan and Weeks (1998), I drew a set of error terms ε_i, for each individual from the extreme value distribution, in order to obtain an estimate that is consistent with the observed activity or inactivity choices. From these drawn values, I select 100 error terms for each individual, in such a way that, when adding it to the deterministic part of the model, it perfectly predicts the activity status that is observed in the survey. In other words, the residual term for an individual that is observed to be a wage earner in the survey should be such that:

\hat{α} + {\hat{β}}_{1} . L o g (R W_{m i}) + {\hat{β}}_{2} . S E X_{m i} + {\hat{β}}_{3} . Q_{m i} + {\hat{β}}_{4} . A R E A_{m} + {\hat{β}}_{5} \cdot C H 6_{m i} + {\hat{β}}_{6} \cdot S C H_{m i} + ε_{m i} > 0,

while, for an individual that is observed to be inactive in the survey, the same inequality should be of opposite sign (≤).

After a policy change, only the deterministic part of the model is recomputed. Then, by adding the random error terms previously drawn to the recomputed deterministic component, a probability distribution over the two alternatives (being a wage worker or being inactive) is generated for each individual. This implies that the model does not assign every individual from the sample to one particular choice, but it gives the individual probabilities of being in one condition rather than in the other. This way, the model does not identify a particular choice for each individual after the policy change, but generates a probability distribution over the different alternatives. This procedure is also described in Creedy and Kalb (2005); see also Creedy et al. (2002b).

3.2 The CGE model

CGE models are a class of economic models that use economic data to estimate how an economy might react to changes in policy, technology or other external factors. A CGE model consists of a system of equations describing model variables and a database consistent with the model equations. General Equilibrium models are used to estimate what is the effect of a change in one part of the economy upon the rest. CGE models have been used widely to analyse trade policy. More recently, CGE has become a popular way to estimate the economic effects of measures to reduce greenhouse gas emissions.

CGE models always contain more variables than equations, so that some variables must be set outside the model. These variables are usually called exogenous variables. The choice of which variables are to be exogenous is called the model closure. Variables defining technology, consumer tastes, and government instruments (such as tax rates) are usually exogenous. For a more detailed introduction to a basic CGE model, please refer to the standard model described in Löfgren et al. (2002).

The CGE model for our economy (all equations are presented in Table 8) is characterized by a representative household who maximizes a Cobb-Douglas utility function with three arguments: leisure and two consumption goods. These commodities are also used as inputs, together with capital and labour, in the production process, which is operated by two firms following a Leontief technology in the aggregation of value added and the intermediate composite good, a Constant Elasticity of Substitution (CES) function for assembling capital and labour into value added, and a Leontief function in the aggregation of intermediate goods. Both factors of production, capital and labour, are mobile among sectors. The capital endowment is exogenously fixed, while labour supply is endogenously determined through household utility maximization (subject to fixed time endowment). The wage elasticity of labour supply is estimated from the household survey, in order to have consistency in labour supply behaviour between the two models. Investments are savings-driven, while government maximizes a Cobb-Douglas utility function to buy consumption goods and uses labour and capital. The public sector also raises taxes on household income, places tariffs on imported goodsand pays transfers to households. For the foreign sector I have adopted the Armington assumption (Armington, 1969) of constant elasticity of substitution for the formation of the composite good (domestic production delivered to domestic market plus imports) which is sold on the domestic market. Domestic production is partially delivered to the domestic market and partially exported, according to a Constant Elasticity of Transformation (CET) function. The small country hypothesis is assumed (the economy is price taker in the world market).

In total the model comprises 49 variables and 41 equations, which, with the 8 exogenous variables (capital endowment, KS, time endowment, TS, public transfers, TF, the four world prices PWE_q and PWM_q, and the numeraire, PC), fully determine the model and allow for satisfaction of Walras’ law (we have a redundant equation).

The calibration of the parameters of the CGE model is done on the basis of a Social Accounting Matrix (SAM) for the economy. A SAM represents the flows of all economic transactions that take place within an economy. SAMs usually refer to a single year, thus providing a static picture of the economy. The columns of a SAM represent buyers (expenditures) and the rows represent sellers (receipts). Columns and rows are added up to ensure accounting consistency, and each column is added up to equal each corresponding row.

The SAM for the economy under study and the initial values of some other variables are consistent with the benchmark situation of the micro-data (for instance, in the benchmark of the two models I have the same average income tax rate, the same average marginal propensity to save, the same budget shares for consumption of the two goods, and so on). The SAM is reported in Table 5. Values of other initial parameters for the CGE module are shown in Table 6, while the variables and equations used in the model can be found in Tables 7 and 8 below. The data in the SAM are in millions of the monetary unit used in the survey.

Table 5

SAM of the economy.

	C₁	C₂	S₁	S₂	K	L	H	G	SI	RoW	Total
C₁			57.5	15.5			95.2	61.2	30.3	23.5	283.3
C₂			17.1	23.5			312.8	48.5	14.2	76.5	492.5
S₁	283.3										283.3
S₂		492.5									492.5
K			72.2	23.0				13.1			108.3
L			83.2	353.8				116.4			553.4
H					108.3	553.4		39.8			701.5
G			12.3	17.7			249.0				279.0
SI							44.5				44.5
*RoW*			41.0	59.0							100.0
*Total*	283.3	492.5	283.3	492.5	108.3	553.4	701.5	269.9	44.5	100.0

Notes: C_q: consumption of good q; S_q: production sector q; K: capital account; L: labour account; H: representative household account; G: public sector; SI: savings-investments account, RoW: Rest of the World account.

Table 6

Values of some parameters for the CGE model.

	Sector 1	Sector 2
Elasticity of substitution (EOS) in production function (aggregation of capital and labour)	0.7	0.5
Elasticity of substitution for Armington composite good	0.7	1.2
Elasticity of transformation for exports and domestic production delivered to the domestic market	−2.0	−3.0
Initial tariff rates on imports	0.3	0.3
Initial time endowment	656.7
Wage elasticity of labour supply (estimated from the household survey)	−0.18665

Table 7

Variables and parameters of the CGE model

Variables		Parameters
PK	Return to capital	ty	Income tax rate
PL	Wage rate	tm_q	Tariff rates on imports
P_q	Price of Armington composite good	ε_LS	Wage elasticity of labour supply
PD_q	Price of output	mps	Marginal propensity to save
PDD_q	Price of domestically produced good delivered to domestic market	αH_q	Cobb-Douglas power of commodity q in RH’s utility function
PWE_q	World price of exports (foreign currency)	αH_l	Cobb-Douglas power of leisure in RH’s utility function
PWM_q	World price of imports (foreign currency)	αCG_q	Cobb-Douglas power of commodity q in government utility function
PM_q	Price of imports (local currency)	αKG	Cobb-Douglas power of capital in government utility function
PE_q	Price of exports (local currency)	αLG	Cobb-Douglas power of labour in government utility function
ER	Exchange rate	io_qs	Technical coefficients
PC	Consumer price index	aF_q	Efficiency parameter production function
KS	Capital endowment (exogenous)	γF_q	Share parameter in production function
LS	Labour supply (endogenous)	σF_q	EOS in firm q’s production function
TS	Time endowment (exogenous)	aA_q	Efficiency parameter in Armington function
X_q	Domestic sales (Armington composite)	γA_q	Share parameter in Armington function
XD_q	Domestic production	σA_q	EOS in firm q’s Armington function
XDD_q	Domestically produced good delivered to domestic market	αI_q	Cobb-Douglas power of commodity q in Bank’s utility function
M_q	Imports	aT_q	Efficiency parameter in CET function
E_q	Exports	γT_q	Share parameter in CET function
K_q	Capital demand by firms	σT_q	Elasticity of transformation in CET function
L_q	Labour demand by firms
I_q	Investment good
C_q	Consumption demand by household
C_l	Demand for leisure
Y	Household’s income
S	Household’s savings
CBUD	Household’s consumption expenditure
TF	Public transfers to household
TAXREV	Tax revenues
CG_q	Consumption demand by government
KG	Capital demand by government
LG	Labour demand by government

Table 8

Equations of the CGE model

Description	Equations
Demand for consumption goods	$P_{q} \cdot C_{q} = α H_{q} \cdot C B U D, where q = 1, 2$
Leisure	$C_{I} = {[(1 - t y) \cdot P L]}^{- 1} \cdot \frac{α H_{I}}{(1 - α H_{I})} \cdot C B U D$
Labour supply	$L S = T S - C_{I}$
Savings	$S = m p s \cdot (1 - t y) \cdot Y$
Consumer price index	$P C = \prod_{q = 1}^{2} P_{q}^{α H_{q}}$
CES production function	$X D_{q} = a F_{q} \cdot {[γ F_{q} \cdot K_{q}^{\frac{(σ F_{q} - 1)}{σ F_{q}}} + (1 - γ F_{q}) \cdot L_{q}^{\frac{(σ F_{q} - 1)}{σ F_{q}}}]}^{\frac{σ F_{q}}{(σ F_{q} - 1)}}$
CES FOC for capital	$K_{q} = \frac{X D_{q}}{a F_{q}} \cdot {(\frac{γ F_{q}}{P K})}^{σ F_{q}} \cdot {[γ F_{q}^{σ F_{q}} \cdot P K^{(1 - σ F_{q})} + {(1 - γ F_{q})}^{σ F_{q}} \cdot P L^{(1 - σ F_{q})}]}^{\frac{σ F_{q}}{(1 - σ F_{q})}}$
Demand for investment goods	$P_{q} \cdot I_{q} = α I_{q} \cdot S$
Price of imports in local currency	$P M_{q} = (1 + t m_{q}) \cdot P W M_{q} \cdot E R$
Price of exports in local currency	$P E_{q} = P W E_{q} \cdot E R$
Armington function	$X_{q} = a A_{q} \cdot {[γ A_{q} \cdot M_{q}^{\frac{(σ A_{q} - 1)}{σ A_{q}}} + (1 - γ A_{q}) \cdot X D D_{q}^{\frac{(σ A_{q} - 1)}{σ A_{q}}}]}^{\frac{σ A_{q}}{(σ A_{q} - 1)}}$
Armington FOC for imports	$M_{q} = \frac{X_{q}}{a A_{q}} \cdot {(\frac{γ A_{q}}{P M_{q}})}^{σ A_{q}} \cdot {[γ A_{q}^{σ A_{q}} \cdot P M_{q}^{(1 - σ A_{q})} + {(1 - γ A_{q})}^{σ A_{q}} \cdot P D D_{q}^{(1 - σ A_{q})}]}^{\frac{σ A_{q}}{(1 - σ A_{q})}}$
CET function	$X D_{q} = a T_{q} \cdot {[γ T_{q} \cdot E_{q}^{\frac{(σ T_{q} - 1)}{σ T_{q}}} + (1 - γ T_{q}) \cdot X D D_{q}^{\frac{(σ T_{q} - 1)}{σ T_{q}}}]}^{\frac{σ T_{q}}{(σ T_{q} - 1)}}$
CET FOC for exports	$E_{q} = \frac{X D_{q}}{a T_{q}} \cdot {(\frac{γ T_{q}}{P E_{q}})}^{σ T_{q}} \cdot {[γ T_{q}^{σ T_{q}} \cdot P E_{q}^{(1 - σ T_{q})} + {(1 - γ T_{q})}^{σ T_{q}} \cdot P D D_{q}^{(1 - σ T_{q})}]}^{\frac{σ T_{q}}{(1 - σ T_{q})}}$
Market clearing condition for labour	$\sum_{q = 1}^{2} L_{q} + L G = L S$
Market clearing condition for capital	$\sum_{q = 1}^{2} K_{q} + K G = K S$
Market clearing condition for commodity q	$X D_{q} + M_{q} \cdot (1 + t m_{q}) = \sum_{s = 1}^{2} i o_{q s} \cdot X D_{q} + C G_{q} + C_{q} + I_{q} + E_{q}$
Income definition	$Y = P K \cdot K S + P L \cdot L S + T F \cdot P C$
Disposable income minus savings	$C B U D = (1 - t y) \cdot Y - S$
Zero profit condition in production function	$P D_{q} \cdot X D_{q} = P K \cdot K_{q} + P L \cdot L_{q} + \sum_{s = 1}^{2} i o_{s q} \cdot X D_{q} \cdot P D_{s}$
Zero profit condition in Armington function	$P_{q} \cdot X_{q} = P M_{q} \cdot M_{q} + P D D_{q} \cdot X D D_{q}$
Zero profit condition in CET function	$P D_{q} \cdot X D_{q} = P E_{q} \cdot E_{q} + P D D_{q} \cdot X D D_{q}$
Demand of commodity q by government	$P_{q} \cdot C G_{q} = α C G_{q} \cdot (T A X R E V - T F \cdot P C)$
Demand of capital by government	$P K \cdot K G = α K G \cdot (T A X R E V - T F \cdot P C)$
Demand of labour by government	$P L \cdot L G = α L G \cdot (T A X R E V - T F \cdot P C)$
Tax revenues	$T A X R E V = t y \cdot Y + \sum_{q = 1}^{2} (t m_{q} \cdot P W M_{q} \cdot E R)$

3.3 Linking the models

The basic difficulty of the top-down approach is ensuring consistency between the micro and macro levels of analysis. For this reason, one may introduce a system of equations to ensure the achievement of consistency between the two models. This way, what happens in the MS module can be made consistent with the CGE modelling by adjusting parameters in the MS model. In practice, this consists in imposing the macro results obtained with the CGE model onto the microeconomic level of analysis. In particular:

changes in the commodity prices, P_q, must be equal to those resulting from the CGE model (Equation (22));
changes in average earnings with respect to the benchmark in the microsimulation module must be equal to changes in the wage rate obtained with the CGE model (Equation (23));
changes in the return to capital of the microsimulation module must be equal to the same changes observed after the simulation run in the CGE model (Equation (24));
changes in the number of wage workers in the microsimulation model must match those observed in the CGE model (Equation (25))

For our model, these consistency conditions translate into the following set of constraints, which could be called linking equations:

C_{q} = \frac{C E_{q}}{(1 + Δ P_{q}^{C G E})}

L o g (Y L_{m i}) = L o g [Y {\hat{L}}_{m i} \cdot (1 + Δ P L^{C G E})]

Y K_{m} = K S_{m} \cdot (1 + Δ P K^{C G E})

\frac{\sum_{m = 1}^{24} \sum_{i = 1}^{N C_{m}} {\hat{W}}_{m i}}{\sum_{m = 1}^{24} \sum_{i = 1}^{N C_{m}} W A_{m i}} \cdot 100 = Δ E M P^{C G E}

The variables with no superscripts are those coming from the microsimulation module; those with the ^ notation correspond to the ones that have been estimated: in particular, Log(ŶL_mi) is the wage level resulting from the regression model for individual i, member of household m, while Ŵ_mi is the labour market status of individual i of household m deriving from the estimation of the binomial choice model.

ΔP_q^CGE, ΔPL^CGE and ΔPK^CGE indicate, respectively, the change in the prices of goods, the change in the wage rate and in the return to capital deriving from the simulation run of the CGE model, while parameter ΔEMP^CGE is the employment level percentage change taken from the CGE framework.

WA_mi is a dummy variable taking value one if individual i of household m is at working age (16–64), and zero otherwise. From Equation (25), the number of employed over the total number of individuals at working age resulting from the MS model must be equal to the change in the employment level observed after the CGE run. This implies that the CGE model determines the employment level of the economy after the simulation, and that the MS model selects which individuals among the inactive persons have the highest probability of becoming employed (if the employment level is increased from the CGE simulation result), or either who, among the wage workers, has the lowest probability of being employed after the policy change (if the employment level is decreased), and, in this case, his/her new wage level will be determined by the regression model of wage earnings (equation (6)).

One possible way of imposing equality between wages and employment at the two levels is through a change in the parameters of the selection and regression models. Following Bourguignon et al. (2003b), this translates into changing the intercepts of function (1) and (2) in the microsimulation module. In other words, changes in average earnings with respect to the benchmark in the microsimulation must be equal to changes in the wage rate obtained with the CGE model, and this is done by adapting intercept a of Equation (6). This just shifts proportionally the estimated wages of all individuals, without causing any change in the ranking between one individual and the other. Likewise, intercept α of the activity status choice function (Equation (7)) is changed to match changed results in the CGE model. This will shift proportionally all the individual probabilities of being a wage worker, without changing their relative positions in the probability distribution, just letting some more individuals to become employed (or some less if the employment rate of the CGE model is decreased), irrespectively of their personal characteristics. This change in the intercept will be of the amount that is necessary to reach the number of wage workers resulting from the CGE model. Thus, this choice preserves the ranking of individuals according to their ex-ante probability of being employed, which was previously determined by the estimation of the binomial model. For this reason the change in the intercept parameter satisfies this neutrality property.

4. The top-down/bottom-up approach

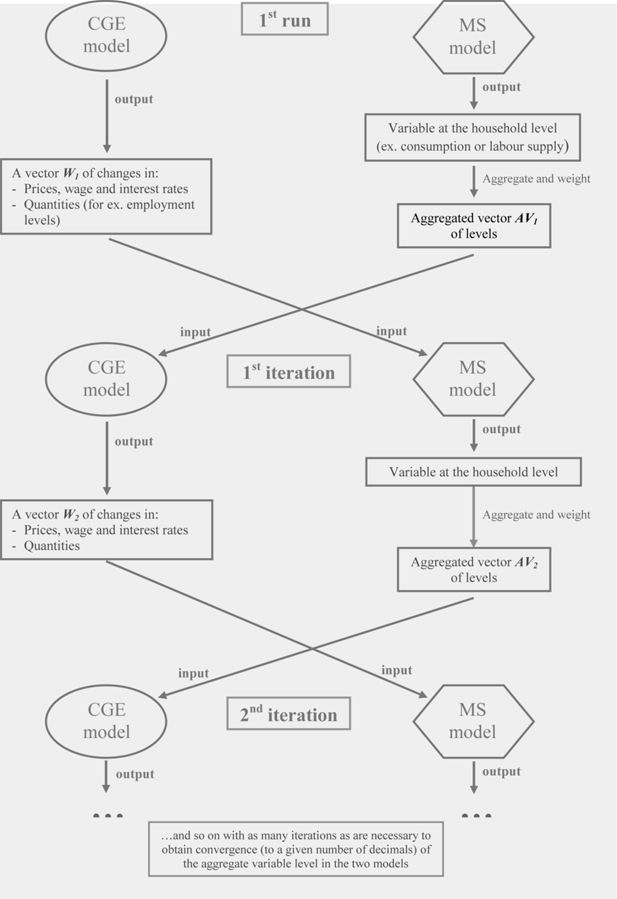
A third approach to linking CGE and MSM was developed by Savard (2003). It attempts to overcome the lack of consistency between the micro and macro levels of the Top-Down approach by introducing a bi-directional link between the two models: for this reason it is also called the “Top-Down/Bottom-Up” approach (TD/BU). According to this method, aggregate results from the MS model (such as consumption levels and/or labour supply) are incorporated into the CGE model, and a loop is used to run both models iteratively until the two produce convergent results.

The value added of this approach is that it takes into account the feedback effects that come from the micro level of analysis, which are completely disregarded by the Top-Down model. The basic assumption behind the TD/BU approach is that the microeconomic effects provided by the MS model run do not correspond to the aggregate behaviours of the representative households used in the CGE model, and that it is thus necessary to take these effects back into the CGE model to fully account for the effects of a simulated policy. A stylized scheme of the way in which this approach works can be observed in Figure 2.

Figure 2

Download asset Open asset

The bilateral communication between the two levels of analysis is achieved through a set of vectors of changes, as in the Top-Down approach: from the macro to the micro level of analysis communication is guaranteed by the changes in the price, wage and return vector and in the employment levels, as before, while for communication from the micro to the macro level I consider in this paper two different strategies: in one, I use as input for the CGE model a vector of changes in the aggregate consumption and in the labour supply levels from the MS model; in the other, only the change in the labour supply level which results from the MS model will be used as input for the CGE model. In either case the process is iterated as many times as is necessary to come to a convergent point, that is, when convergence (at a certain number of decimals) is obtained in the aggregate variable levels of the two models.

The choice for consumption and labour supply as communicating variables is made following Savard (2003). However, as both consumption and labour supply are not exogenous in the CGE model, some of the initial hypotheses of the model must be changed. First, I remove the equations determining consumption demand by the representative household (the first equation in Table 8), substituting them with the following single equation:

C B U D = \sum_{i = 1}^{2} P_{i} \cdot C_{i} .

In the initial hypothesis (endogenous consumption) I had two endogenous variables (C_i) and two equations. Now I have two exogenous variables and one equation. As I need to insure the balancing of the household’s budget constraint, a variable needs now to be endogenized in the following equation:

\begin{array}{l} C B U D = (1 - m p s) \cdot (1 - t y) . \\ (P K \cdot K S + P L \cdot L S + T F) . \end{array}

Following Savard, I choose to endogenize the marginal propensity to save, mps, which is now a variable that changes in order to satisfy the budget constraint. In addition, I introduce an exogenous level of labour supply into the CGE model, and just leave out the equation that determines the demand for leisure (the second equation in Table 8). This way, the third equation will now yield the demand for leisure as the time remaining after having supplied an exogenous level of labour. In the second variant of the TDBU model, I introduce an exogenous level of labour supply into the CGE model, but omit the equation that determines the demand for leisure (the second equation in Table 8).

5. Simulation

Having outlined three alternative approaches to integrating CGE with microsimulation models, in this section I compare the results from each when used to simulate the same ‘policy’. The simulation will be of an exogenous shock to the world price level of the good exported by sector 2, which is the labour intensive sector in our stylized economy. In this shock the world price of good 2 is reduced by 64% from its initial value.

The simulation results for the most relevant macroeconomic variables are reported in percentage changes in Tables 9 and 10. The macroeconomic results for the Top-Down model (shown in the second columns of the tables) represent the results that would emerge from a “stand-alone” CGE model, since they come from a simple run of the CGE model. These macroeconomic changes are then imposed onto the microsimulation model, as explained in Section 3.3, in order to obtain results at the micro level, which are shown in Tables 11 and 12.

Table 9

Simulation results: percentage changes (CGE model).

	Integrated Approach	Top-Down Approach	TD/BU Approach (C&LS)	TD/BU Approach (LS)
Government Surplus	0.00	0.00	0.00	0.00
Wage Rate	−14.87	−14.67	−14.42	−14.64
Capital Return	19.70	19.30	17.91	19.13
Consumer Price Index	0.00	0.00	0.00	0.00
Exchange Rate	53.83	53.76	53.83	53.70
Labour Supply	−1.00	−1.18	−1.32	−1.32
Government Use of Labour	4.82	4.23	3.72	4.06
Government Use of Capital	−25.45	−25.45	−24.72	−25.43
Income*	−9.50	−9.39	−9.50	−9.48
Disposable Income*	−9.50	−9.39	−9.50	−9.48
Consumption Expenditure*	−9.50	−9.39	−7.90	−9.48
Marginal Propensity to Save	0.00	0.00	−16.22	0.00
Savings*	−9.28	−9.39	−24.18	−9.48
Tax Revenues	−9.28	−9.48	−9.63	−9.58

*

For the integrated model, these changes are computed as average percentage changes across households.

Table 10

Simulation results: percentage changes (CGE model).

Macro variables	Integrated Approach		Top-Down Approach		TD/BU Approach (C&LS)		TD/BU Approach (LS)
Macro variables	Sector 1	Sector 2	Sector 1	Sector 2	Sector 1	Sector 2	Sector 1	Sector 2
Commodity Prices	−0.99	0.30	−1.23	0.38	−1.70	0.52	−1.27	0.39
Domestic Sales	−8.69	−12.52	−8.81	−12.54	−10.21	−12.05	−8.88	−12.64
Domestic Production	27.81	−14.20	27.91	−14.31	26.77	−13.86	27.84	−14.43
Labour Demand	43.52	−13.22	43.05	−13.36	41.08	−12.94	42.88	−13.48
Capital Demand	13.07	−26.82	13.14	−26.72	12.72	−25.84	13.15	−26.76
Consumption*	−8.60	−9.78	−8.26	−9.73	−6.58	−8.30	−8.32	−9.84
Investment	−7.65	−8.84	−8.26	−9.73	−22.87	−24.57	−8.32	−9.84
Imports	−32.92	−47.63	−33.11	−47.57	−34.37	−47.21	−33.16	−47.60
Exports	207.36	−78.38	209.23	−78.53	209.10	−78.48	209.11	−78.59

*

For the integrated model, these changes are computed as average percentage changes across households.

Table 11

Simulation results: Inequality indices on disposable per capita real income (MS model).

	Benchmark Values	Integrated Approach*	Top-Down Approach*	TD/BU Approach (C & LS)*	TD/BU Approach (LS)*
Gini Index	31.85	3.02%	1.68%	1.52%	1.66%
Atkinson’s Index, ε = 0.5	8.46	4.94%	3.01%	2.72%	2.97%
Coefficient of Variation	65.86	3.78%	2.84%	2.64%	2.81%
Generalized Entropy Measures:
I(c), c = 2	21.69	7.69%	5.75%	5.35%	5.70%
Mean Logarithmic Deviation, I(0)	17.72	3.99%	2.10%	1.83%	2.07%
Theil Coefficient, I(1)	17.82	5.89%	3.89%	3.58%	3.85%

*

Percentage deviations from benchmark values.

Table 12

Simulation results: Poverty indices on disposable per capita real income (MS model).

	Benchmark Values	Integrated Approach*	Top-Down Approach*	TD/BU Approach (C & LS)*	TD/BU Approach (LS)*
General Poverty Line
Headcount Index, P₀	40.98	56.00%	8.00%	8.00%	8.00%
Poverty Gap Index, P₁	9.84	119.46%	27.25%	27.01%	27.21%
Poverty Severity Index, P₂	0.00	143.04%	28.95%	28.51%	28.88%
Extreme Poverty Line
Headcount Index, P₀	4.92	166.67%	33.33%	33.33%	33.33%
Poverty Gap Index, P₁	1.00	71.09%	4.77%	4.64%	4.75%
Poverty Severity Index, P₂	0.00	45.33%	−0.03%	0.03%	−0.03%

*

Percentage deviations from benchmark values.

In all tables, the two different strategies adopted for the TD/BU approach are also taken into account, allowing comparison of the results arising from two different ways of taking into account the feedback effects from the micro level of analysis. This is done by introducing into the CGE model, as inputs derived from the microsimulation module, the consumption level and labour supply (C&LS), or the labour supply only (LS).

In general, for most of the macro variables, similar results are produced by all four simulations. The shock has negative effects on the economy. Indeed, as I can observe in Table 10, the fall in the price of the exported good for sector 2 causes a reduction of the production level for this sector, which reduces its demand for both factors of production. However, due to the depreciation of local currency, the reduction in the level of exports is lower than the 64% world price reduction. For the same reason, exports for the other production sector become more convenient, so that for this sector I observe an increase in the level of the exported good, an increase in the production level, and in the demand for capital and labour. The depreciation of local currency also has a negative effect on the level of imports, which contributes to a decrease in the amount of goods sold on the domestic market.

The second sector is labour-intensive, as can be observed in the SAM (Table 5). Therefore the level of labour demand as a whole falls, generating a reduction in the wage rate, which causes a decrease in labour supply. The opposite is observed for capital, as the first sector is more capital-intensive. As a consequence of the change in the price of the factors, government increases its demand for labour input and decreases the demand for capital, as the latter has become relatively more expensive.

As the income of the representative household is based chiefly on the supply of labour, we observe a reduction in nominal income and, as a consequence, of savings and consumption expenditure. The amount of consumption goods always decrease, but the percentage change varies according to the change in their relative price: the commodity produced by the second sector has become relatively more expensive, due to the negative shock that hit the sector.

As investments are savings-driven, we also observe a reduction in the demand for investment goods (again, the investment good produced by the second sector is now relatively more expensive, so I observe a higher reduction for the demand of this good).

However, one particular result needs further explanation: savings and investments in the TD/BU-C&LS model decrease much more than in the other three models. The reason for this lies in the fact that, in order to be able to introduce exogenous consumption levels into the CGE model, I had to endogenize one variable in the households’ budget constraint to keep the equilibrium in this constraint. Savard’s choice is for the marginal propensity to save, and I have followed his approach. But the consequence of this will be a change in household behaviour with respect to the initial assumptions made for the benchmark. Indeed, as Table 9 shows, the marginal propensity to save of the household decreased markedly; hence the greater decline in households’ savings. As in our model investments are savings-driven, this in turn generates a further reduction of investments relative to the other models (Table 10). I will analyse this aspect further in the next Subsection (5.1).

In Tables 11 and 12, the first column shows the “Benchmark Values”, that is the values of the indices computed from the cross-sectional dataset, while the other columns indicate the percentage deviations from these values for the four models. The underlying variable for the computation of the poverty and inequality indices is per capita real disposable income, which is obtained by dividing disposable income by the household specific consumer price index. The latter is computed using households’ consumption shares and the change in prices deriving from the CGE model, as follows:

C P I_{m} = \sum_{q = 1}^{2} η_{m q} \cdot (1 + Δ P_{q}^{C G E}) .

In order to obtain per capita income, real households’ income is then divided by the number of adult equivalents, as defined by the OECD-modified scale proposed by Hagenaars et al. (1994).

With respect to the microeconomic results, specifically those relating to changes in poverty and inequality, we can observe in Table 11 and 12 that the differences in results are generally significant only for the case of the integrated model. Indeed, the models following the layered approach (namely the Top-Down and TD/BU models) show rather similar results for both inequality and poverty measures changes. Only for the TD/BU-C&LS model do we observe a smaller effect on inequality, which increases less than in the other two models, though the change goes in the same direction. Results concerning poverty measures show practically identical changes for the three models following the layered approach. In contrast, for the integrated approach we observe larger differences in results, especially in the poverty measures. The reason is that, in this approach, the negative effect of the shock on the labour market is uniformly distributed across all households, whereas in the layered models the role played by the binary equation for labour market status in the microsimulation module is very important, since it selects the individuals with the higher probability of losing their job.

The higher increase in inequality in the integrated approach is also confirmed by the higher level of the Severity of Poverty Index, which measures the degree of inequality among the poor, and a higher Poverty Gap Index, which indicates that the gap between the income of the poor and the poverty line has increased.

5.1 More on the TD/BU approach

In this subsection I want to investigate further what happens within the TD/BU approach in general, and in particular I want to explore the main cause of the unusual deviation that is observed in the level of savings under the TD/BU-C&LS approach.

As a first intuition, such a deviation could be generated either by a problem of initial data inconsistency between the two datasets (the SAM and the survey), or by what I will refer to as “feedback effects” from the microeconomic level of analysis. With this concept I intend to incorporate all the effects that derive from a response (behavioural or not) of the agents in the MS model that is different from the one observed in the CGE model for the Representative Household (RH). This difference could be due either to a different way of modelling a particular behaviour in the two models (for instance, in the case of labour supply, the MS model uses a discrete and individualized concept of labour supply, while in the CGE model I have a continuous labour supply defined for the RH), or simply to the fact that in the MS model I consider single households as the unit of modelling, while in the CGE model I have a unique RH (as for consumption and savings, for instance).

In order to check whether the problem derives from an initial data inconsistency, I will run the same model using a new Social Accounting Matrix, which has been built in such a way that it is fully consistent with the relevant survey aggregates. In Table 13, the SAM values that were adjusted to survey data are those in the grey cells. The remaining columns and rows were then rebalanced, using least squares minimization, to obtain consistency. By comparing this SAM with the original one in Table 5, we can observe that in our case initial data inconsistencies were not very big (the biggest inconsistency is observed in the savings level of the households: here 41.7 while in the original SAM of Table 5 it was 44.5).

Table 13

SAM of the economy made consistent with the Household Survey.

	C₁	C₂	S₁	S₂	K	L	H	G	SI	RoW	Total
C₁			57.8	15.6			95.4	62.6	28.1	23.6	283.0
C₂			17.1	23.5			313.2	48.8	13.6	76.6	492.8
S₁	283.3										283.0
S₂		492.5									492.8
K			73.4	23.2				13.2			109.8
L			81.7	353.8				117.5			552.6
H					109.8	552.6		38.7			701.2
G			12.3	17.7			250.8				280.8
SI							41.7				41.7
*RoW*			40.8	59.4							100.2
*Total*	283.0	492.8	283.0	492.8	109.8	552.6	701.2	280.8	41.7	100.2

Notes: C_q: consumption of good q; S_q: production sector q; K: capital account; L: labour account; H: representative household account; G: public sector; SI: savings-investments account, RoW: Rest of the World account.

Using the SAM shown in Table 13, I simulated the impact of a shock on the export price of sector 2 (−64%) as before. Results are reported in Tables 14 and 15 for the C&LS and LS variants of the TD/BU approach. Observing the result for savings in the TD/BU-C&LS approach, we can see that in our case data inconsistencies were responsible only for a 2% change in the marginal propensity to save and in the savings level. This means that the remaining change of around 13% (the difference between the change observed in the other approaches, around 9%, and the one observed in this approach, 22.24%) is to be attributed to the feedback effects from the MS model.

Table 14

Simulation results with consistent data: Percentage changes (CGE model).

	TD/BU Approach (C & LS)	TD/BU Approach (LS)
Government Surplus	0.00	0.00
Wage Rate	−14.63	−14.81
Capital Return	18.36	19.37
Consumer Price Index (num.)	0.00	0.00
Exchange Rate	53.90	53.80
Labour Supply	−1.18	−1.18
Government Use of Labour	4.13	4.42
Government Use of Capital	−24.89	−25.48
Income	−9.45	−9.43
Disposable Income	−9.45	−9.43
Consumption Expenditure	−8.14	−9.43
Marginal Propensity to Save	−14.13	0.00
Savings	−22.24	−9.43
Tax Revenues	−9.57	−9.52

Table 15

Simulation results with consistent data: Percentage changes (CGE model).

	TD/BU Approach (C & LS)		TD/BU Approach (LS)
	Sec 1	Sec 2	Sec 1	Sec 2
Commodity Prices	−1.44	0.44	−1.07	0.33
Domestic Sales	−9.86	−12.06	−8.89	−12.55
Domestic Production	26.77	−13.80	27.65	−14.27
Labour Demand	41.65	−12.85	43.17	−13.30
Capital Demand	12.70	−25.99	13.05	−26.76
Consumption	−7.13	−8.45	−8.45	−9.73
Investment	−21.11	−22.58	−8.45	−9.73
Imports	−34.12	−47.30	−33.10	−47.63
Exports	207.50	−78.34	207.46	−78.43

Observing the results for the TD/BU-LS approach I discover instead that the change in labour supply that was observed after the first iteration (−1.32% instead of −1.18% of the first iteration) was due only to a problem of data inconsistency and not to feedback effects from the MS model. This means that modelling labour supply as a discrete choice and individually in the MS model does not affect the results of the macro model in a significant way, at least in this particular case.

Having established that in the case of the TD/BU-C&LS approach most of the deviation in the savings level (13% against a 2% due to data inconsistencies) is to be attributed to the feedback effects coming from the micro level of analysis, I now want to understand which variable or parameter most affects this deviation. Intuitively, and as we have already seen with the TD/BU-LS approach, the different method of modelling labour supply does not have a big effect. Thus, this deviation in the savings level must be due to the fact that in the MS model expenditure shares and tax parameters are specific to every single household, while in the CGE model there is only one RH group with “average” shares and parameters. (In this sense ours is an extreme case, as there is only one RH in the CGE model). In order to understand which is the parameter that most particularly affects the deviation in savings level, I next ran the MS model using for all households the RH’s shares taken from the CGE model, rather than the shares and parameters observed for each household in the survey. The communicating variables from the MS model to the CGE model remained the ones used in the TD/BU-C&LS approach, that is consumption levels and labour supply.

Results in Table 16 clearly indicate that the main cause of difference between the two models is to be detected in the income tax rate, while labour supply and expenditure shares account only for a small part of it (the change in the savings level remains at 22% in these cases). As a result of deriving all parameters from the CGE model (labour supply change, income tax rate, mps and consumption shares), the deviation in the savings level is almost reduced to zero, as was to be expected.

Table 16

TD/BU-C&LS approach with consistent data: RH shares from CGE model used in the MS model (percentage changes, CGE model).

	only ty	only ΔLS	only η_i & mps	ΔLS, ty, mps & η_i
Marginal propensity to save Savings	2.92	−14.82	−14.47	0.12
Savings	−6.78	−22.87	−22.55	−9.33

These results are not surprising, as the income tax rate in the MS model is modelled in a way that is not linear with respect to the income level; rather, the rate depends on the income brackets to which household income belongs. Of course this feature is not captured at all in the CGE model, where the unique tax rate for the RH that is merely proportional to its income. Under the TD/BU-C&LS approach, while transmitting the consumption level from the MS to the CGE model, also implicitly transmitted was a level of disposable (after tax) income that was incompatible with the one in the CGE model (in both our models, consumption and savings are simply modelled as fixed proportions of disposable income). In principle, I could introduce a non-linear equation in the CGE model in order to represent this non-linearity of the tax system. However, even with this equation, the CGE model would not be able to capture the income changes deriving from a change of labour market status for the individual agents, which is the main cause of change of income tax bracket. These occupational changes are instead taken into account in the microsimulation model with the occupational status function (Equation (2)). These kind of switching regime functions are difficult to implement in a system of simultaneous equations like a CGE model; and in any case these kinds of equations would not make sense in a CGE model with Representative Households instead of individual households, such as the one I am working with at this stage.

As a consequence of our modelling choices, made following Savard (2003), all the effect of the mismatching between the disposable income levels of the two models is going into the change in the marginal propensity to save, then into the savings and investments levels as a consequence, but is not being transmitted in a significant way to the rest of the economy. Indeed, given the results in Tables 9 and 10, I might be tempted to say that, except for these big deviations in savings and investments levels (and a lower difference in the level of consumption), for the rest feedback effects do not appear to bring about significant differences in the results. This is even more evident once I have eliminated the effects coming from data inconsistencies (see Tables 14 and 15 compared with the columns for the Top-Down approach of Tables 9 and 10).

But the deviation in the savings level is quite big, even after having eliminated the problem of data inconsistency, and it allows us to believe that all the effects from the micro level of analysis are absorbed by the change in savings (and consequently of investments), and only in a very small part are they transmitted to the rest of the economy. Thus, a doubt arises: is consumption in our case the right variable to pass the feedback effects onto the CGE model?⁵ And was the choice of leaving the marginal propensity to save free to vary in the CGE model the best channel for transmitting these feedback effects to the whole economy?

Which is the parameter I have seen to be driving the biggest change between the micro and the macro level? It is income the tax rate, which is in our case the main determinant of disposable income. A next step, therefore, is to try to use this parameter (conveniently “aggregated” into a representative one), together with the change in aggregate labour supply, as communicating variables from the MS model to the CGE model. In doing so I will try to use not only the income tax rate from the MS model, but also the marginal propensity to save and the consumption shares.

Results are shown in Tables 17 and 18. As we can see by comparing these results with the ones in Table 9 and 10 for the Top-Down approach, feedback effects from the micro level of analysis can be important. In particular, in our case, we observe a different path for disposable income and tax revenues (due to the reduction of the income tax rate), and for savings and consumption, whose percentage changes are now closer to the ones of the MS model (see Table 19). Ultimately, full consistency between the CGE and the MS model results is only obtained when working with consistent data and when all the parameters (change in labour supply, tax rates, marginal propensity to save and consumption shares) are transmitted to the CGE model. However, if I report all these parameters from the MS model into the CGE model without having previously adjusted the data, we can see in Tables 17 and 18 that the problem of data inconsistency comes out again and distorts the results of the CGE model, and especially the level of savings (and that of investments as a direct consequence). Indeed the level of savings was one of the biggest sources of data inconsistency between the SAM and the survey.

Table 17

Simulation results TD/BU approach: percentage changes (CGE model).

	ΔLS & ty (inconsistent data)	ΔLS, ty, mps & η_i (inconsistent data)	ΔLS, ty, mps & η_i (consistent data)
Government Surplus	0.00	0.00	0.00
Wage Rate	−14.70	−14. 62	−14.84
Capital Return	19.43	18.95	19.46
Consumer Price Index (num.)	0.00	0.00	0.00
Exchange Rate	53.90	53.95	54.02
Labour Supply	−1.18	−1.18	−1.18
Government Use of Labour	2.26	2.13	1.62
Government Use of Capital	−26.96	−26.69	−27.55
Income	−9.39	−9.40	−9.44
Disposable Income	−8.47	−8.48	−8.12
Consumption Expenditure	−8.47	−7.93	−8.14
Marginal Propensity to Save	0.00	−5.53	0.25
Savings	−8.47	−13.54	−7.89
Tax Revenues	−10.95	−10.97	−11.60

Table 18

Simulation results TD/BU approach: percentage changes (CGE model).

	ΔLS & ty (inconsistent data)		ΔLS, ty, mps & η_i (inconsistent data)		ΔLS, ty, mps & η_i (consistent data)
	Sec 1	Sec 2	Sec 1	Sec 2	Sec 1	Sec 2
Commodity Prices	−1.21	0.37	−1.38	0.42	−1.09	0.33
Domestic Sales	−8.75	−12.00	−9.27	−11.77	−8.92	−11.73
Domestic Production	28.13	−13.75	27.72	−13.53	27.87	−13.42
Labour Demand	43.37	−12.79	42.66	−12.58	43.46	−12.44
Capital Demand	13.28	−26.30	13.11	−25.93	13.20	−26.07
Consumption	−7.35	−8.81	−6.90	−8.24	−7.45	−8.35
Investment	−7.35	−8.81	−12.33	−13.91	−6.88	−8.19
Imports	−33.09	−47.31	−33.57	−47.16	−33.20	−47.23
Exports	210.17	−78.31	210.17	−78.27	208.79	−78.11

Table 19

Simulation results TD/BU approach: percentage changes (MS model).

	ΔLS & ty (inconsistent data)		ΔLS, ty, mps & η_i (inconsistent data)		TD Approach (inconsistent data)
	Sec 1	Sec 2	Sec 1	Sec 2	Sec 1	Sec 2
Consumption	−7.23	−8.28	−7.45	−8.35	−7.21	−8.28
Savings		−7.78		−7.88		−7.78

At this point I would like to draw attention to another important fact: the Top-Down approach suffers not only from the problem of a lack of feedback effects from the micro level of analysis; it is not even exempt from the problem of data inconsistency. The reason that the results of the two models (the micro and the macro model) do not coincide could be due to either a problem of initial data inconsistency, or to a difference in the microeconomic behaviour of the agents in the MS model. In either case, one has to decide which results are the most reliable ones.

Having considered the impact of model variants on macroeconomic factors, Tables 20 and 21 report the impacts on income inequality and poverty changes of the simulated shock, for two of the three models described above.

Table 20

Inequality indices on disposable per capita real income (MS model).

	Benchmark Values	ΔLS & ty (inconsistent data)*	ΔLS, ty, mps & η_i (consistent data)*
Gini Index	31.85	1.70%	1.66%
Atkinson’s Index, ε = 0.5	8.46	3.04%	2.97%
Coefficient of Variation	65.86	2.86%	2.81%
*Generalized Entropy Measures*:
I(c), c = 2	21.69	5.80%	5.70%
Mean Logarithmic Deviation, I(0)	17.72	2.13%	2.07%
Theil Coefficient, I(1)	17.82	3.93%	3.85%

*

Percentage deviations from benchmark values

Table 21

Poverty indices on disposable per capita real income (MS model).

	Benchmark Values	ΔLS & ty (inconsistent data)*	ΔLS, ty, mps & η_i (consistent data)*
*General Poverty Line*
Headcount Index, P₀	40.98	8.00%	8.00%
Poverty Gap Index, P₁	9.84	27.30%	27.21%
Poverty Severity Index, P₂	0.00	29.01%	28.88%
*Extreme Poverty Line*
Headcount Index, P₀	4.92	33.33%	33.33%
Poverty Gap Index, P₁	1.00	4.79%	4.75%
Poverty Severity Index, P₂	0.00	−0.03%	−0.03%

*

Percentage deviations from benchmark values

As we can see, no big differences are observed with respect to the results of the layered models as reported in Tables 11 and 12. This means that, at least in our case, taking into account feedback effects does not have a strong influence on the results on income distribution and poverty change. These results also confirm, once again, the fact that the integrated approach tends to overestimate the effects of the shock on income inequality and poverty changes, even though at the macro level I do not observe significant deviations in the main macroeconomic variables (see Tables 9 and 10).

6. Conclusion

CGE models alone, by normally following the Representative Household approach, are unable to capture individual and household heterogeneity. Microsimulation models, in contrast, are partial equilibrium analyses: change in prices, other markets and especially the demand side of the labour market are missing elements, that in reality are crucial for a complete analysis of a reform affecting also the macroeconomic side of the economy. Integration of the two approaches, connecting a microsimulation model to a macro-economic model, offers significant potential for improving the economic analysis of a reform involving both macro and micro sides of the economy. However, linking CGE and microsimulation models might prove to be a cumbersome and time-consuming exercise in some cases. Before starting such an endeavour, therefore, the researcher should weigh the advantages and disadvantages of implementing a linked micro-macro model, carefully evaluating the scope and purposes of the analysis he/she wants to run.

In this paper I have presented a considered evaluation of the merits and demerits of the alternative methods currently used to link CGE and microsimulation models, with a focus on static models. Using data from a fictitious economy, I built three models: one that follows the full integrated approach, as in Cockburn (2001); one that follows the so called Top-Down approach, as developed in Bourguignon et al. (2003b), and one that follows the method developed by Savard (2003), also known as Top-Down/Bottom-Up model.

As a result of this evaluation, I have demonstrated that a simple integrated approach, at least as implemented in this paper, is deficient with regards to the microeconomic specification and behavioural responses of individual agents, whilst the introduction of microeconometric behavioural equations into a CGE model looks difficult to implement and cumbersome from a computational point of view. I have also been able to show (Section 5.1) that a Top-Down approach completely disregards the possible feedback effects coming from the microeconomic side of the economy, which could affect also the macroeconomic variables.

My results also suggest the, in comparison, TD/BU modelling looks the most complete approach, as on the one hand it can include all the microeconometric estimates required to account for behavioural responses by individual agents, and on the other take into account the feedback effects from the micro to the macro level of analysis: “…The value added of this approach comes from the fact that feedback effects, provided by the household model, do not correspond to the aggregate behaviours of the representative households used in the CGE model» (Savard, 2003: 20)”.

However, as my comparative evaluation has shown, two main problems arise when using the TD/BU approach. First of all, the way in which feedback effects are reported to the CGE model can affect results in a fundamental way. The use of shares or parameters, instead of absolute levels⁶, when possible, seems to lead to more consistent results, in particular because when transmitting absolute levels from the MS model one has to change the initial hypothesis of the CGE model (see Section 4). Secondly, eventual data inconsistencies between the micro and the macro datasets can also affect results seriously. This can only be overcome by adjusting one or other dataset, thus going back to the problem of data reconciliation encountered with the integrated model (see Section 2). However, whereas with an integrated model this problem is inevitably encountered when building the model, in a TD/BU model it is possible to run the model without previously adjusting the data. In this latter case, however, one is left unable to distinguish which is the part of the resulting change that is due to feedback effects and which is the part due to data inconsistencies.

Footnotes

1.

For early applications of this type of models, see Adelman and Robinson (1978) and Dervis et al. (1982), who specified lognormal within-group distributions with exogenous variances. More recent examples of this kind of models can be found in Decaluwé et al. (1999a), Colatei and Round (2000) and Agénor et al. (2001).

2.

After Mookherjee and Shorrocks’ (1982) study of UK, there are now other examples of “within/between” decomposition analysis of changes in inequality that indicate that changes in overall inequality are usually due at least as much to changes in within-group inequality as to changes in the between-group component. Among the applications to developing countries, see Ahuja et al. (1997), who applied this decomposition analysis to the case of Thailand, and Ferreira and Litchfield (2001) for Brazil.

3.

There exist different principles on which SAM-balancing programs can be based, such as the “Row and Sum” or RAS method (see Bacharach, 1971), least squares minimization principles, known also as Stone-Byron methods (see Stone (1977) and Byron (1978)), or the more recent cross-entropy approach proposed by Robinson et al. (2001) and Robilliard and Robinson (2003).

4.

The Extreme Value distribution (Type I) is also known as Gumbel (from the name of the statistician who first studied it) or double exponential distribution, and it is a special case of the Fisher-Tippett distribution. It can take two forms: one is based on the smallest extreme and the other on the largest. I will focus on the latter, which is the one of interest for us. The standard Gumbel distribution function (maximum) has the following probability and cumulative density functions, respectively:

\begin{array}{l} pdf : f (x) = \exp (- x - e^{- x}) \\ CDF : F (x) = \exp (- e^{- x}) . \end{array}

5.

Remember that in our case consumption is not modelled in a significantly different way in the two models. However, there could be other cases where the level of consumption can be an important carrier of feedback effects from the micro level of analysis.

6.

c.f. Savard (2003), in which consumption levels are used.

References

1
Income Distribution Policy in Developing Countries: A Case Study of Korea
1. I Adelman
2. S Robinson
(1978)
Oxford: Oxford University Press.
- Google Scholar
2
IMMPA: A Quantitative Macroeconomic Framework for the Analysis of Poverty Reduction Strategies
(2001)
Washington: The World Bank.
- Google Scholar
3
Everyone’s miracle? Revisiting poverty and inequality in East Asia. Directions in Development
1. V Ahuja
2. B Bidani
3. F Ferreira
4. M Walton
(1997)
Washington: The World Bank.
- Google Scholar
4
A Theory of Demand for Products Distinguished by Place of Production. IMF Staff Paper
1. PS Armington
(1969)
159–176, A Theory of Demand for Products Distinguished by Place of Production. IMF Staff Paper, 16.
- Google Scholar
5
On the measurement of inequality
1. AB Atkinson
(1970)
Journal of Economic Theory 2:244–263.
- Google Scholar
6
Bi-proportional Matrices and Input-Output Change
1. M Bacharach
(1971)
Cambridge: Cambridge University Press.
- Google Scholar
7
Un modèle CGE-Multi-Ménages Intégrés Appliqué à l’économie Sénégalaise
(2003)
miméo, CREA, Dakar, Codesria.
- Google Scholar
8
Representative versus real households in the macro-economic modelling of inequality. DT/2003/10
(2003b)
DIAL/Unité de recherche CIPRE.
- Google Scholar
9
Globalisation and Poverty Changes: A Case Study on Colombia. Working Paper No. 226
1. M Bussolo
2. J Lay
(2003)
Paris: OECD Development Centre.
- Google Scholar
10
The Estimation of Large Social Accounting Matrices
1. RP Byron
(1978)
Journal of the Royal Statistical Society, Series A, 141, 3.
- Google Scholar
11
Trade Liberalization and Poverty in Nepal: A Computable General Equilibrium Micro-simulation Approach. Working Paper 01-18
1. J Cockburn
(2001)
CRÉFA, Université Laval.
- Google Scholar
12
Formation du revenue, segmentation et discrimination sur le marché du travail d’une ville en développement: Antananarivo fine de siècle. DIAL DT/2001-18
1. D Cogneau
(2001)
Formation du revenue, segmentation et discrimination sur le marché du travail d’une ville en développement: Antananarivo fine de siècle. DIAL DT/2001-18.
- Google Scholar
13
Growth, distribution and poverty in Madagascar: Learning from a Microsimulation Model in a General Equilibrium Framework. IFPRI TMD Discussion Paper No. 61 and DIAL DT/2001-19
1. D Cogneau
2. A-S Robilliard
(2001)
Growth, distribution and poverty in Madagascar: Learning from a Microsimulation Model in a General Equilibrium Framework. IFPRI TMD Discussion Paper No. 61 and DIAL DT/2001-19.
- Google Scholar
14
Poverty Alleviation Policies in Madagascar: A MicroMacro Simulation Model. DT/2004/11
1. D Cogneau
2. A-S Robilliard
(2004)
DIAL/Unité de Recherche CIPRÉ.
- Google Scholar
15
Simulating targeted policies with macro impacts: Poverty Alleviation Policies in Madagascar
1. D Cogneau
2. A-S Robilliard
(2006)
Paris: IRD, DIAL.
- Google Scholar
16
Poverty and Policy: Some Experiments with a SAM-Based CGE Model for Ghana
1. D Colatei
2. J Round
(2000)
mimeo, Warwick University.
- Google Scholar
17
Trade Reform and Poverty in the Philippines: a Computable General Equilibrium Microsimulation Analysis. Working Paper 05-13
1. CB Cororaton
2. J Cockburn
(2005)
CIRPÉE.
- Google Scholar
18
Discrete hours labour supply modelling: specification, estimation and simulation
1. J Creedy
2. G Kalb
(2005)
Journal of Economic Surveys 19:697–734.
- Google Scholar
19
Microsimulation Modelling of Taxation and The Labour Market: The Melbourne Institute Tax Transfer Simulator
1. J Creedy
2. A Duncan
3. M Harris
4. R Scutella
(2002b)
Cheltenham: Edward Elgar.
- Google Scholar
20
Combining microsimulation with CGE and macro modelling for distributional analysis in developing and transition countries
1. J B Davies
(2009)
International Journal Of Microsimulation 2:49–65.
- Google Scholar
21
Poverty Analysis within a General Equilibrium Framework. Working Paper No. 9909
(1999a)
African Economic Research Consortium.
- Google Scholar
22
Measuring Poverty and Inequality in a Computable General Equilibrium Framework, Cahier de recherche du CRÉFA No. 99-20
(1999)
Measuring Poverty and Inequality in a Computable General Equilibrium Framework, Cahier de recherche du CRÉFA No. 99-20.
- Google Scholar
23
General Equilibrium Models for Development Policy
(1982)
New York: Cambridge University Press.
- Google Scholar
24
Simulating transitions using discrete choice models
1. A Duncan
2. M Weeks
(1998)
Papers and Proceedings of the American Statistical Association 106:151–156.
- Google Scholar
25
Education or Inflation? The Micro and Macroeconomics of the Brazilian Income Distribution During 1981–1995
1. FHG Ferreira
2. JA Litchfield
(2001)
Cuadernos de Economia 38:209–238.
- Google Scholar
26
Poverty Statistics in the Late 1980s: Research Based on Micro-data
(1994)
Luxembourg: Office for Official Publications of the European Communities.
- Google Scholar
27
The common structure of statistical models of truncation, sample selection and limited dependent variables and a simple estimator for such models
1. JJ Heckman
(1976)
Annals of Economic and Social Measurement 5:475–492.
- Google Scholar
28
Sample Selection Bias as a Specification Error
1. JJ Heckman
(1979)
Econometrica 47:153–162.
- Google Scholar
29
A Micro-Macro Model for South Africa: Building and Linking a Microsimulation Model to a CGE Model. Melbourne Institute Working Paper Series, WP No. 16/05
1. N Hérault
(2005)
A Micro-Macro Model for South Africa: Building and Linking a Microsimulation Model to a CGE Model. Melbourne Institute Working Paper Series, WP No. 16/05.
- Google Scholar
30
A standard Computable General Equilibrium (CGE) model in GAMS, 5
(2002)
Washington D.C.: International Food Policy Research Institute (IFPRI).
- Google Scholar
31
Models of Growth and Distribution for Brazil
1. FJ Lysy
2. L Taylor
(1980)
The General Equilibrium Income Distribution Model, Models of Growth and Distribution for Brazil, Oxford, Oxford University Press, Chapter 6.
- Google Scholar
32
A Decomposition Analysis of the Trend in UK Income Inequality
1. D Mookherjee
2. A Shorrocks
(1982)
Economic Journal 92:886–902.
- Google Scholar
33
Reconciling Household Surveys and National Accounts Data Using a Cross Entropy Estimation Method
1. A-S Robilliard
2. S Robinson
(2003)
Review of Income and Wealth 49:395–406.
- Google Scholar
34
Updating and Estimating a Social Accounting Matrix Using Cross Entropy Methods
(2001)
Economic Systems Research 13:49–64.
- Google Scholar
35
Poverty and Income Distribution in A CGE-Household Micro-Simulation Model: Top-Down/Bottom-Up. ApproachCIRPÉE. Working Paper 03-43
1. L Savard
(2003)
Poverty and Income Distribution in A CGE-Household Micro-Simulation Model: Top-Down/Bottom-Up. ApproachCIRPÉE. Working Paper 03-43.
- Google Scholar
36
Social Accounting for Development Planning with Special Reference to Sri Lanka
1. R Stone
(1977)
Forward to, Social Accounting for Development Planning with Special Reference to Sri Lanka, London, Cambridge University Press.
- Google Scholar

Article and author information

Author details

Giulia Colombo

Department of Economic and Social Science - Catholic University of Milan and SiNSYS NV/SA

For correspondence
giulia.colombo@sinsys.net

Acknowledgements

I would like to thank Stefan Boeters for his comments and suggestions.

Publication history

Version of Record published: August 31, 2018 (version 1)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Download citations (links to download the citations from this article in formats compatible with various reference manager tools)

BibTeX
RIS

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

The Top-Down approach.

Description of the subscripts for the microsimulation model.

Direct income tax rates.

Heckman selection model, two-step estimates.

Binary logit model of labour status choice.

SAM of the economy.

Values of some parameters for the CGE model.

Variables and parameters of the CGE model

Equations of the CGE model

The Top-Down/Bottom-Up approach.

Simulation results: percentage changes (CGE model).

Simulation results: percentage changes (CGE model).

Simulation results: Inequality indices on disposable per capita real income (MS model).

Simulation results: Poverty indices on disposable per capita real income (MS model).

SAM of the economy made consistent with the Household Survey.

Simulation results with consistent data: Percentage changes (CGE model).

Simulation results with consistent data: Percentage changes (CGE model).

TD/BU-C&LS approach with consistent data: RH shares from CGE model used in the MS model (percentage changes, CGE model).

Simulation results TD/BU approach: percentage changes (CGE model).

Simulation results TD/BU approach: percentage changes (CGE model).

Simulation results TD/BU approach: percentage changes (MS model).

Inequality indices on disposable per capita real income (MS model).

Poverty indices on disposable per capita real income (MS model).

Author details

Giulia Colombo

For correspondence

Downloads (link to download the article as PDF)

Download citations (links to download the citations from this article in formats compatible with various reference manager tools)

Open citations (links to open the citations from this article in various online reference manager services)

Categories and tags