1. Methodology
  2. Spatial microsimulation
Download icon

A review of spatial microsimulation methods

  1. Robert Tanton  Is a corresponding author
  1. Institute for Governance and Policy Analysis, University of Canberra, Australia
Research article
Volume 7(1) Spring 2014
Cite this article as: R. Tanton; 2014; A review of spatial microsimulation methods; International Journal of Microsimulation; 7(1); 4-25. doi: 10.34196/ijm.00092

Abstract

This paper outlines a framework for spatial microsimulation models, gives some reasons why someone may want to use a spatial microsimulation model, describes the development of spatial microsimulation over the last 30 years, summarises the different methods currently used for spatial microsimulation, and outlines how the models can be validated.

In reviewing the reasons and methods for spatial microsimulation, we conclude that spatial microsimulation provides an alternative to other small area estimation methods, providing flexibility by allowing cross-tabulations to be built, and an ability to link to other models, and derive projections. Spatial microsimulation models also allow demographic changes, like births and deaths, to be included in a dynamic microsimulation model. This also allows ‘what if’ scenarios to be modelled, for example, what would happen if the birth rate increased over time.

Validation of the spatial microsimulation models shows that they are now at the stage where they can provide reliable results.

1. Introduction

Deriving indicators for small areas has become an important part of statistical research over the last few years. Policy makers want to know indicators for electorates (Department of Parliamentary Services, 2009), researchers recognise the importance of spatial disadvantage (Tanton et al., 2010; Procter et al., 2008), and the public want to hear how their community is going in terms of indicators like income, poverty rates, or inequality. This has led to an increase in the number of articles on spatial disadvantage, as evidenced by the references in this article.

There have been a number of methods in the statistical sciences used to derive spatial indicators, and these methods are commonly called small area estimation. They have been reviewed by Pfeffermann (2002). Recently, there has been another set of methods for small area estimation coming from the microsimulation area, and a recent paper and book have reviewed these spatial microsimulation methods (Hermes & Poulsen, 2012; Tanton and Edwards, 2013).

There are a number of advantages of a spatial microsimulation approach over a traditional small area estimation approach. The main advantage is that using spatial microsimulation, a synthetic microdata file for each small area is derived. This means that while traditional small area estimation methods produce a point estimate, spatial microsimulation can produce cross tabulations– so a user can look at poverty by age group and family type (Tanton, 2011). These small area estimates could be used by Government for planning purposes (Harding et al., 2009; Harding et al., 2011) and by researchers for looking at spatial disadvantage (Miranti et al., 2010; Tanton et al., 2010).

Having a synthetic microdata file for each small area also means that populations can be updated dynamically using fertility and mortality rates (Ballas et al., 2007a), so a dynamic spatial microsimulation model can be used to analyse effects of demographic changes in small areas.

Another advantage of spatial microsimulation is that the model can potentially be linked to another model to derive small area estimates from the other model. An example is deriving small area estimates from a Tax/Transfer microsimulation model (Tanton et al., 2009; Vu & Tanton, 2010) and deriving small area estimates from a CGE model, as described in another paper in this issue (Vidyattama et al., 2014).

Given the amount of work in this field recently, it is useful to summarise the different methods, and attempt to put them into a methodological framework. This paper does this, but also identifies some of the advantages and disadvantages of each method, and compares and contrasts the different methods. This is useful for someone looking at designing a spatial microsimulation model, as it provides a summary of all the methods and their advantages and disadvantages in one place. The methodological framework also helps a new user understand how each of the methods fits with the other methods.

The first section in this paper develops a framework for classifying spatial microsimulation methods. The next two sections outline the methods under static and dynamic headings. The next section discusses what to consider in choosing a model; and the final section concludes.

2. A framework for spatial microsimulation methods

Before looking at methods for spatial microsimulation models, it may be useful to try to categorise the different methods into groups. This provides the reader with an easy way to classify each method.

As a first step, like normal microsimulation models, spatial microsimulation models can be either static or dynamic. Dynamic microsimulation models take a base dataset, age this dataset over time, and model certain life events including marriage, deaths and births. They usually use probabilities to model these life events.

Static microsimulation models do not model life events, so the proportion of people married (and in fact, the people married on the base dataset) does not change. A static microsimulation model recalculates certain attributes, like incomes or eligibility for legal-aid services, using the unit record data on the base dataset. Static microsimulation models are usually used for rules based systems, where it is easy to use a rule to calculate pension eligibility or the amount of tax a household should pay based on a set of rules.

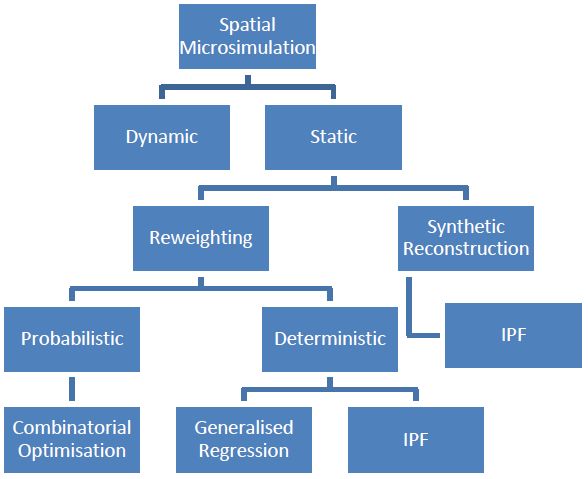
Both these types of models are also relevant for spatial microsimulation models, and this paper will use these two types of models to review the literature. Within each of these two types of models, there are then different methods to calculate the small area estimates. Under a static model, there is a reweighting method and a synthetic reconstruction method.

These different methods are shown in Figure 1, which is based on the description in Ballas et al. (2005a). It can be seen that there are two broad methods for static spatial microsimulation: reweighting and synthetic reconstruction. The reweighting method uses a number of different techniques to adjust survey weights from a national survey so that the sample represents small areas rather than national totals. The synthetic reconstruction method creates a new dataset for each small area, so microdata from a national survey is not necessary.

Figure 1
Download asset Open asset
Methods of spatial microsimulation.

3. Static spatial microsimulation methods

This section describes the different static spatial microsimulation models identified in the above framework.

3.1 Synthetic reconstruction

The synthetic reconstruction method creates a synthetic list of individuals and households where the characteristics of the individuals, when aggregated, will match known aggregates from another data source in the area being estimated. The starting point may be to create a population that matches a known Age/Sex distribution; and then this population might be adjusted to reflect a known labour force distribution; and then occupation or industry could be added. These characteristics are matched sequentially, rather than all at once.

There are a few different methods used for synthetic reconstruction, but the main method used is Iterative Proportional Fit (Birkin & Clarke, 1988; 1989). The IPF method builds up a synthetic dataset for a small area using Census tables to create an entirely synthetic dataset.

This method is described in detail by Birkin and Clarke, and was used in the SYNTHESIS model (Birkin & Clarke, 1988). To generate a vector of individual characteristics in an area x = (x1,x2,…,xm), a joint probability distribution needs to be created, p(x). As information is rarely available for the full joint distribution, it needs to be built up one attribute at a time, so the probability of the different attributes is conditionally dependent on existing (known) attributes:

(1) p(x)=p(x1)*p(x2x1)*p(x3x2,x1)*…*P(xmxm−1,…,x1)

The problem is how to use as much information as possible for the right hand side of this equation. This means estimating the joint probability distribution p(x1, x2,x3) subject to known joint probabilities p(x1,x2) and p(x1,x3).

If we let the first approximation of p(x1, x2,x3) = 1/N1N2N3, where N1, N2 and N3 are the number of states attributed to x1,x2 and x3, then the vector x can be adjusted by the known states:

(2) p2(x1,x2,x3)=p1(x1,x2,x3)p(x1,x2)∑x1p1(x1x2x3)
(3) p3(x1,x2,x3)=p2(x1,x2,x3)p(x1,x2)∑x1p2(x1x2x3)

These equations are iterated until the probabilities reach a certain acceptable limit. Williamson et al. use this same estimation methodology in early work (Clarke et al., 1997; Williamson et al., 1996). This synthetic reconstruction method should not be confused with the reweighting method that also uses IPF described below. The main difference between the two is that the reweighting IPF method starts with a record unit dataset, whereas the synthetic IPF method does not.

One of the advantages of the synthetic reconstruction method is that it does not require a microdata set, as it creates a synthetic microdata set. Many statistical agencies, including the Office of National Statistics (ONS) in the UK and the Australian Bureau of Statistics (ABS) in Australia, provide microdata files of their surveys (called Confidentialised Unit Record Files, or CURF‘s in Australia). However, in some cases a CURF is not available so a synthetic unit record dataset is required. One example in Australia is the Indigenous Social Survey, which is a survey conducted by the Australian Bureau of Statistics for which a CURF is not released due to confidentiality restrictions. A synthetic reconstruction method was therefore used to create a synthetic dataset which a generalised regression spatial microsimulation model could then be applied to. This is described in Vidyattama et al. (2013).

3.2 Reweighting

There are many different ways to reweight a microdata file, and many different variations and modifications to the general techniques. However, generally the techniques can be categorised into two broad groups: a method that selects individuals from the microdata file to fill the area and a method that adjusts the original weights on the microdata file. Most applications of spatial microsimulation will fit into one of these two groups (although see Other Methods below for some cases that do not fit into these groups).

The first group selects individuals from the microdata, until the sample selected for the small area looks like the small-area totals from some other source (usually a Census). These individuals can be randomly selected, but there is usually some intelligence in the selection algorithm. This is the method that Combinatorial Optimisation uses.

The other set of methods are reweighting methods. These usually use formulae to adjust some initial weights to better fit the small area benchmarks. There are two reweighting methods described below, IPF (Ballas et al., 2005a) and a generalised regression method (Tanton et al., 2011; Singh & Mohl, 1996).

3.2.1 Combinatorial optimisation

This method is a mathematical process that finds an optimal object from a finite set of objects. Applied to spatial microsimulation, the process is used to choose which records from a survey best represent a small area (Williamson, 1996; Williamson, 2007).

It is an iterative approach which selects a combination of households from the microdata to reproduce, as closely as possible, the population in the small area. The process starts with a random selection from the microdata, and then looks at the effect of replacing one household. If the replacement improves the fit to some small-area benchmarks, then it is chosen; if not, the original household is replaced and another household is chosen to replace it. This process is repeated, with the aim of gradually improving the fit.

Because the process is iterative, a decision needs to be made as to when to stop the process. This could be time elapsed, number of iterations reached, or accuracy level reached. The approach used by most users of this technique is a level of accuracy called the Total Absolute Error, which is the difference between the estimated totals and the benchmark totals, squared (so it is the absolute error) and summed for all benchmark tables and all areas.

An assessment of this technique by Voas and Williamson (Voas & Williamson, 2000) found that the results were reasonable for any variables that were part of the set of constraint tables. However, estimating cross-tabulations for variables that were not in the list of constraints resulted in a poor fit.

The worst case scenario for this method is that every single combination of households is assessed to find the best fit. This maximises the time taken for the procedure to run. Further developments of the combinatorial optimisation techniques built some intelligence into the searching for records to select from the microdata, rather than randomly selecting records (Williamson et al., 1998).

The first technique for intelligently searching for records tested was a hill-climbing approach. This approach selects a combination of records to be replaced, and then selects one record to replace a record in the combination. This reduces the number of combinations to be tested. While this technique is faster than randomly selecting from the whole microdata file, the procedure can still get stuck in sub-optimal solutions. Better solutions may exist, but because of a replacement made earlier, the optimal solution will not be found. In testing this method, Williamson et al. observed that the hill climbing routine was getting sub-optimal solutions (Williamson et al., 1998).

The next technique tested to make the CO algorithm more efficient was called simulated annealing. This allows the algorithm to climb down from sub-optimal solutions by allowing changes to the combination being optimised even if they make the solution worse (in terms of the Total Absolute Error, TAE, as described above).

The choice of whether or not to accept a worse replacement is determined by an equation from thermo-dynamics:

(4) p(δE)=exp(−δET)

where δE is the potential increase in energy and T is the absolute temperature.

In applying this to the combinatorial optimisation technique, T is set to the maximum change in performance likely by replacing an old element with a new one, and δE is the increase in the TAE. As replacement elements are selected, any that make the fit better are accepted, and any that make the fit worse are accepted if p(δE) is greater than or equal to a randomly generated number. Note that an important element of this formula is that smaller values of δE (change in TAE as a result of the replacement) lead to a greater likelihood of a change being made.

The main problem with this method is that T, the initial temperature, has to be set. This temperature is also reduced over time, to simulate the cooling process in thermo-dynamics. Williamson et al. suggest reducing T by 5% if the number of successful replacements carried out is in excess of some set maximum. So there are three parameters to set – initial temperature, number of swaps before reducing the temperature, and the extent of reduction made each time. Williamson et al. test a number of different parameters in their paper (Williamson et al., 1998).

Williamson et al. found that this simulated annealing method performs much better than the hill climbing algorithms, but also noted that to obtain the best solution, the amount of backtracking needs to be as small as possible. This means setting the parameters of the simulated annealing algorithm to minimise the back tracking. Williamson et al. stated that an initial temperature of 10 and a reduction in temperature of 5% after 100 successful swaps provided optimum results.

This combinatorial optimisation with simulated annealing technique has also been used in a static version of the SMILE spatial microsimulation model for Ireland (Hynes et al., 2009; Hynes et al., 2006) and in a model called Micro-MaPPAS, which is an extension of SimLeeds (Ballas et al., 2007b).

Very recently, Farrell et al. have described a probabilistic reweighting algorithm that is similar to CO with simulated annealing called quota sampling (Farrell et al., 2013). It selects random households from the micro-dataset and considers them for admittance into the area level population if they improve the fit to the benchmark tables. Unlike simulated annealing, quota sampling only assigns households to an area if they improve the fit, and once a household is selected for a small area, they are not replaced. This sampling without replacement improves the efficiency of the method.

Another method for intelligent sampling suggested by Williamson et al. was a genetic algorithm. These algorithms were developed to imitate nature evolving towards ‘optimal’ solutions through natural selection. This process assesses each combination for ‘fitness’, and the fittest chromosomes are chosen to be ‘parents’, generating a new set of ‘child’ solutions. A random element is introduced through ‘mutation’, which is a low level chance of mis-translation between parents in reproduction. This mutation is important to introduce diversity into the population of possible solutions.

The problem with this method is that there are a number of parameters that need to be determined, and testing by Williamson et al. found that the genetic algorithm procedures worked worse that the hill climbing and simulated annealing process (Williamson et al, 1998). Birkin et al. has also used a GA algorithm to calculate the base population for their model MOSES (Birkin et al, 2006), and found that the method performed poorly in terms of the accuracy of the results.

3.2.2 IPF method

One of the problems with the CO method is that because it is probabilistic, for each run of the model, a different result will be given. This is because the records from the microdata are randomly selected, and assuming a purely random selection of records from the microdata (so, in computing terms, a different seed is used each time for the random-number generator), a different set of households will be selected each time the procedure is run.

Another way to derive a micro data file for each small area is to reweight a current national micro data file to small area benchmarks from another source. One way to do this is described in Ballas et al. (Ballas et al., 2005a) and Edwards and Clarke (2013). The starting point for the reweighting is the weights usually provided in the sample microdata, which take into account the sample selection probability, and are adjusted for partial and full non response and any known bias. For each constraint variable, the reweighting algorithm adjusts these start weights to the constraint table using the formula:

(5) ni=wi*sh/mh

Where wi is the original weight for household i, ni is the new weight, sh is data for the small area benchmark h from a Census (for example), and mh is the data from the microdata for that same cross-tabulation h (eg, Age by Sex).

This adjustment of the weights is done for each constraint. The process is described in detail with a worked example in Anderson (2013).

One of the perceived problems with this method is that many of the households used to populate the small area can come from out of the area. Research by Tanton and Vidyattama shows that in most cases this isn’t a problem, but for smaller cities in Australia it can be (Tanton & Vidyattama, 2010). Ballas overcame this problem by using geographical multipliers, so households from within the area had a higher weight than households outside the area. These weight multipliers were then used to adjust the final weights (Ballas et al., 2005c).

This procedure gives non-integer weights, so Ballas then uses another procedure to force these weights to be integer so each record on the microdataset represents a whole number of people (Ballas et al., 2005c).

This method has also been used by Procter et al. (Procter et al., 2008; Edwards & Clarke, 2013) for estimating obesity.

3.2.3 Generalised regression

The first proponent of the generalised regression method was Melhuish at the National Centre for Social and Economic Modelling (NATSEM) at the University of Canberra, and it was later significantly developed by others at NATSEM, including using the model for small-area policy analysis; adding significant validation to the model; and adding projections to the model (Melhuish et al., 2002; Tanton et al., 2009; Tanton et al., 2011; Harding et al., 2011).

The method is similar to the IPF method, in that it reweights a national unit record file to small area benchmarks, but differs in the way this reweighting is conducted. This method uses the same generalised regression reweighting method used to reweight Australian surveys to National and State benchmarks. In summary, the generalised regression method starts with the weights provided on the microdata. In Australia, these have been adjusted for the sample design (clustering, stratification, oversampling), and then usually benchmarked to Australian totals. These initial weights are divided by the population of the area to provide a reasonable starting weight required for the generalised regression procedure.

The generalised regression procedure uses a regression model to calculate a new set of weights, given the constraints provided for each small area. These weights are limited to being positive weights only, which means the procedure may iterate a number of times if positive weights aren’t achieved for every record in the first run. The process takes an initial weight from the survey, and continually adjusts this weight until reasonable results are achieved, or until a maximum number of iterations has been reached. A full description of the method is in Tanton et al. (Tanton et al., 2011).

The model has been used to derive estimates of poverty (Tanton et al., 2010; Tanton et al., 2009; Tanton, 2011), housing stress (McNamara et al., 2006; Phillips et al., 2006), Wealth (Vidyattama et al., 2011), subjective wellbeing (Mohanty et al., 2013) and Indigenous disadvantage (Vidyattama et al., 2013).

One of the advantages of this method is that projections are very easy to create, either by inflating the weights; or inflating the benchmarks and reweighting to new benchmarks (Harding et al., 2011). This method for projecting has also been used for SimBritain by Ballas (Ballas et al., 2007a).

The other use that has been made of this model is for policy analysis for small areas, achieved by linking the model to a Tax/Transfer microsimulation model run by NATSEM called STINMOD (Harding et al., 2009; Tanton et al., 2009).

There are some potential limitations of the SpatialMSM model, and these have all been tested in a paper by Tanton and Vidyattama (Tanton & Vidyattama, 2010). This paper tested three different aspects of the model:

  1. increasing the number of benchmarks;

  2. using a restricted sample for estimating some areas in Australia; and

  3. using univariate constraint tables rather than multivariate constraints.

The authors found that the model stood up well to this testing. The authors added a number of benchmarks, and found that adding another two benchmarks decreased the level of accuracy slightly, and increased slightly the number of small areas failing an accuracy criterion. The advantage of the additional benchmarks was that the final dataset was more general – so it could now be used for estimating education outcomes or occupation, as these were the two new benchmark datasets added.

Using univariate benchmarks gave more usable areas, but with a reduced level of accuracy for these areas.

Using records from the area being estimated (for example, not using Sydney records to populate Canberra SLA’s) did not have a huge effect on many areas, but did affect some smaller capital cities in Australia, so more accurate estimates were derived for Adelaide and Perth.

3.3 Other methods

While the framework above tries to categorise the methods, there are obviously methods that fall outside of these categories. For example, Birkin et al. used an Iterative Proportional Sampling method, which appears to be a sampling and then reweighting method for their Population Reconstruction Model in MOSES. The procedure uses a random sample from the Sample of Anonymised Records; constructs cross tabulations from this synthetic population and compares this to the actual populations for the small area; and then adjusts the weights upwards for attributes under-represented in the area and downwards for attributes over-represented. This process is iterated until acceptable results were achieved (Birkin et al., 2006).

A very early implementation of spatial microsimulation used a spatial-interaction model and allocated individuals using allocation models solved at an aggregate level (Clarke & Wilson, 1985). These allocation models included housing and labour market models, fed from national economic forecasts.

3.4 Comparison of methods

Synthetic reconstruction and combinatorial optimisation methodologies for the creation of small-area synthetic microdata have been examined by Huang and Williamson (2001). They found that outputs from both methods can produce synthetic microdata that fit constraint tables very well. However, the dispersion of the synthetic data has shown that the variability of datasets generated by combinatorial optimisation is much less than by synthetic reconstruction, at ED and ward levels. The main problem for the synthetic reconstruction method is that a Monte Carlo solution is subject to sampling error which is likely to be more significant where the sample sizes are small.

The ordering of the conditional probabilities in the synthetic reconstruction method can also be a problem as synthetic reconstruction is a sequential procedure. Another drawback of synthetic reconstruction is that it is more complex and time consuming to program. The outputs of separate combinatorial optimisation runs are much less variable and much more reliable. Moreover, combinatorial optimisation allows much greater flexibility in selecting small area constraints. Huang and Williamson conclude that combinatorial optimisation is much better than synthetic reconstruction when used to generate a single set of synthetic microdata.

In this issue, Tanton et al. compare the CO and Generalised Regression methods (Tanton et al., 2014). The main problem with the SpatialMSM model at the time was the number of areas that a solution could not be found for, whereas the CO method was able to nearly always get an estimate for an area. The generalised regression algorithm used in SpatialMSM is also much slower than the CO algorithm, although much has now been done since then to make the generalised regression algorithm more efficient.

The CO method gave slightly better results compared to the generalised regression algorithm, in terms of measures of accuracy.

4. Dynamic spatial microsimulation

Dynamic Spatial Microsimulation is one of the most complex forms of spatial microsimulation, and the most data intensive. It requires raw data for each of the small areas as a starting point for the modelling. These raw data are then updated using probabilities derived from other sources. For the best results, these probabilities also need to be available for each small area, although probabilities for larger areas could be applied to the smaller areas if there is not much spatial variability in the raw data being updated. For instance, birth rates do not vary much for very small areas, so some aggregation could be used.

There are a number of examples of dynamic spatial microsimulation models, and the examples shown here are SVERIGE in Sweden, MOSES and SIMBritain (a pseudo-dynamic model) in Britain, SMILE in Ireland and CORSIM in the US.

The SVERIGE model (Rephann, 2004; Vencatasawmy et al., 1999) uses longitudinal socio-economic information on every resident in Sweden from 1985 – 1995 with co-ordinates accurate to 100 m. This is a very powerful longitudinal dataset of all Swedes, and allows for very complex modelling.

The SVERIGE model has 10 modules, each with a set of rules that determine the occurrence of specific events in a person’s life. Events are generated through deterministic models of behaviour and a monte carlo simulation. These behaviours are functions of individual, household and regional socio-economic characteristics.

For example, the mortality module uses two sets of mortality equations, one for those under 25; and one for those over 25. For those under 25, historical mortality rates by age and sex are used to decide whether a person dies. For those aged over 25, a regression model is used to calculate the probability that the person will die in that year. This regression model includes age, marital status, family earnings, education level, sex and whether working.

There are ten modules in SVERIGE:

  • Fertility;

  • Education;

  • Employment and Earnings;

  • Cohabitation and Marriage;

  • Divorce/Dehabitation;

  • Leaving home;

  • Immigration;

  • Emigration;

  • Internal migration;

  • Mortality.

Each of these modules is run using either a sample of the full population (to test a scenario); or the full population of Sweden (to minimise the risk of error). The sequence in which the modules are applied is the same as the list above.

The next dynamic spatial microsimulation model is MOSES, by Birkin et al. in the UK (Birkin et al., 2009). This model starts with a synthetic database of everyone in the UK, so it uses a Population Reconstruction Model (Birkin et al., 2006) that provides considerable spatial detail. There are a number of demographic processes modelled, including Birth, Death, Marriage, Household Formation, Health, Migration and Housing. All these are modelled using transition probabilities calculated from the Census, ONS Vital Statistics (for Births and Deaths) and the British Household Panel Survey. People are also aged forward for each year modelled. It has been used in the UK for demographic and health projections. The main difference between MOSES and SVERIGE is that MOSES uses a synthetic dataset of everyone in the UK, whereas SVERIGE uses a geocoded dataset of everyone in Sweden. This means that, in theory, SVERIGE will provide more accurate modelling.

Another dynamic microsimulation model is a version of SMILE (Spatial Microsimulation model for Ireland), which is a model for Ireland (Ballas et al., 2005b; 2006; Hynes et al., 2006). This model uses the Life-Cycle Analysis Model (O’Donoghue et al., 2009), which is a framework for dynamic microsimulation models that includes how data are stored in a relational database, the processes for ageing, birth, death, and migration.

Two processes are used in SMILE, a static spatial microsimulation model to create a base population for each area and a dynamic ageing process for this base population. The static model used for the dynamic version of SMILE uses an IPF method, described elsewhere in this paper. The dynamic part of the model uses probabilities to model mortality, fertility and internal migration, similar to SVERIGE.

The CORSIM model has been in development at Cornell University in the US since 1986 (Caldwell et al., 1998). The CORSIM model incorporates 50 economic, demographic and social processes using about 900 stochastic equations and rule-based algorithms and 17 national microdata files. The model also projects forward to 2030. The model is modularised with a number of modules including a wealth module (Caldwell & Keister, 1996). While the CORSIM model has been used extensively in the past, little has been published from the model recently.

Pseudo-dynamic spatial microsimulation models are models that use static spatial microsimulation and some dynamic component. One example is SimBritain (Ballas et al., 2007a). This model is both a static and a dynamic spatial microsimulation model. It uses the British Household Panel Survey and the Small Area Statistics (SAS) tables from the British Census to derive a synthetic population for each small area. A dynamic spatial microsimulation approach is then used to update this synthetic dataset.

The method used to derive the synthetic base file for the first year is a probabilistic synthetic reconstruction method which uses Iterative Proportional Fitting (IPF) to generate a vector of individual characteristics on the basis of a joint probability distribution from the SAS tables.

Once this base dataset for each area is created, the future population is calculated. This is where the dynamic element of this model is introduced. Mortality and fertility are based on location-specific probabilities. Fertility is a function of age, marital status and location. Monte-Carlo sampling against the fertility probabilities of each female is used to determine which females give birth, and if a birth occurs then a new individual with age 0, sex determined probabilistically, single, and social class and location that of the mother is created.

SimBritain is not as comprehensive a dynamic model as the other models described in this section, and could be described as a pseudo-dynamic model. It incorporates a static element and then a dynamic element (modelling fertility and mortality).

It can be seen from this review that these models are data intensive. There is only one model in this review (SVERIGE) that uses actual data from the whole population to do the microsimulation modelling. All other models create synthetic small-area data for the microsimulation modelling. Not only is record-unit data required for each small area being estimated, but transition probabilities for each small area are required to update the populations. This can mean up to 900 equations (as used in the CORSIM model), and each equation will require updating at some time. Without this regular updating, and regular funding to update the models, they can get out of date very quickly, and they become unusable over time.

5. Which method to use

This summary of spatial microsimulation methods shows that each of the methods have particular advantages and disadvantages. Dynamic models can provide projections and can incorporate demographic change, but are very data intensive and complex due to requiring formulae for each area. If demographic projections are required, or some scenarios include demographic change, then a dynamic or pseudo-dynamic model will be required. Static models are much less data intensive and easier to design and calculate, but projections are based on external sources, and are not based on formulae within the model, so in most cases cannot be adjusted.

In terms of outputs, all static models provide the same sort of output file – a micro-data file (whether synthetic or weighted) for small areas. Further, Tanton et al., in this volume, show that at least two of the methods derive very similar results (Tanton et al., 2014). The decision on which method to use then comes down to

  1. Availability of a unit record file. If no unit record file is available, then synthetic reconstruction is the only method to use.

  2. Availability and experience in a programming language or a particular method. For example, the generalised regression procedure is written in the SAS language. SAS is an expensive program to purchase, and may be out of reach for many researchers. Further, an application has to be made to the Australian Bureau of Statistics to get access to the GREGWT SAS Macro. There are spatial microsimulation procedures built into the R library SMS (Kavroudakis, 2013), which is free to download, making it more accessible.

6. Conclusions

This paper has classified the methods used for spatial microsimulation, reviewed the different methods used, and assessed the different methods.

We find that spatial microsimulation has been around as a method for small area estimation since the 1980’s, and has developed significantly in this time. It is now at the stage where it provides an excellent alternative to other small area estimation methods, providing flexibility by allowing cross-tabulations to be built, an ability to link to other models, and projections.

Dynamic spatial microsimulation models allow demographic changes, like births and deaths, to be included into the analysis. This also allows for more complex ‘what if’ scenarios, for example, what would happen if the birth rate increased over time. However, these models are data intensive, complex and expensive to update.

Static spatial microsimulation methods are much less data intensive, and many of the methods are readily available. Code exists for some procedures in R (Kavroudakis, 2013) and other code is in SAS and FORTRAN.

In terms of choosing a spatial microsimulation method, this comes down to data availability (whether a unit record data file is available), the experience of the staff programming the model, and what programming languages are available.

The development of spatial microsimulation models over the last 30 years has been through a fairly small core of people, but as the methods and results get published in peer reviewed journals, they are becoming more accepted in different fields. Policy makers in Government and the general public are also becoming much more interested in the results from spatial microsimulation models as the models can provide new cross-tabulations of data which were not available through traditional small area estimation methods. They can also link to other models like Tax/Transfer microsimulation models to provide small area estimates of a tax/transfer policy change.

References

  1. 1
    Estimating Small Area Income Deprivation: An Iterative Proportional Fitting Approach
    1. Ben Anderson
    (2013)
    In: Tanton, Edwards, editors. Spatial Microsimulation: A Reference Guide for Users. Springer. pp. 49–67.
  2. 2
    Using SimBritain to Model the Geographical Impact of National Government Policies
    1. D Ballas
    2. G Clarke
    3. D Dorling
    4. D Rossiter
    (2007a)
    Geographical Analysis 39:44–77.
    https://doi.org/10.1111/j.1538-4632.2006.00695.x
  3. 3
    Geography matters: Simulating the local impacts of National social policies
    1. D Ballas
    2. D Rossiter
    3. B Thomas
    4. G Clarke
    5. D Dorling
    (2005a)
    York: Joseph Rowntree Foundation.
  4. 4
    Building a dynamic spatial microsimulation model for Ireland
    1. D Ballas
    2. G Clarke
    3. E Wiemers
    (2005b)
    Population, Space and Place 11:157–172.
    https://doi.org/10.1002/psp.359
  5. 5
  6. 6
  7. 7
  8. 8
  9. 9
    The Generation of Individual and Household Incomes at the Small Area Level using Synthesis
    1. M Birkin
    2. M Clarke
    (1989)
    Regional Studies: The Journal of the Regional Studies Association 23:535–548.
    https://doi.org/10.1080/00343408912331345702
  10. 10
    A Synthetic Demographic Model of the UK Population : Methods, Progress and Problems
    1. M Birkin
    2. A Turner
    3. B Wu
    (2006)
    Proceedings of the Second international conference on e-Social Science.
  11. 11
    Moses: Dynamic spatial microsimulation with Demographic Interactions
    1. M Birkin
    2. B Wu
    3. P Rees
    (2009)
    In: A Zaidi, A Harding, P Williamson, editors. New frontiers in Microsimulation Modelling. Ashgate. pp. 53–77.
  12. 12
    Modelling regional changes in US household income and wealth: a research agenda
    1. S Caldwell
    2. G Clarke
    3. A Keister
    (1998)
    Environment and Planning C: Government and Policy 16:707–722.
    https://doi.org/10.1068/c160707
  13. 13
    Wealth in America: family stock ownership and accumulation, 1960–1995
    1. S Caldwell
    2. L Keister
    (1996)
    In: G Clarke, editors. Microsimulation for Urban and Regional Policy Analysis. London: Pion. pp. 88–116.
  14. 14
    Estimating Small Area Demand for Water: A New Methodology
    1. G Clarke
    2. A Kashti
    3. A McDonald
    4. P Williamson
    (1997)
    Water and Environment Journal 11:186–192.
    https://doi.org/10.1111/j.1747-6593.1997.tb00114.x
  15. 15
    The Dynamics of Urban Spatial Structure: The Progress of a Research Programme
    1. M Clarke
    2. A Wilson
    (1985)
    Transactions of the Institute of British Geographers 10:427–451.
  16. 16
    Poverty rates by electoral divisions
    1. Department of Parliamentary Services
    (2009)
    Canberra: Commonwealth of Australia.
  17. 17
    SimObesity: Combinatorial Optimisation (Deterministic) Model
    1. K Edwards
    2. G Clarke
    (2013)
    In: Tanton, Edwards, editors. Spatial Microsimulation: A Reference Guide for Users. Springer. pp. 69–85.
  18. 18
    Creating a Spatial Microsimulation Model of the Irish Local Economy
    1. Niall Farrell
    2. Karyn Morrissey
    3. Cathal O’Donoghue
    (2013)
    In: Tanton, editors. Spatial Microsimulation: A Reference Guide for Users. Springer. pp. 105–125.
  19. 19
  20. 20
  21. 21
    A review of current methods to generate synthetic spatial microdata using reweighting and future directions
    1. K Hermes
    2. M Poulsen
    (2012)
    Computers, Environment and Urban Systems 36:281–290.
    https://doi.org/10.1016/j.compenvurbsys.2012.03.005
  22. 22
    A Comparison of Synthetic Reconstruction and Combinatorial Optimisation Approaches to the Creation of Small-Area Microdata. Working paper 2001/02
    1. Z Huang
    2. P Williamson
    (2001)
    Department of Geography, University of Liverpool.
  23. 23
    A spatial micro-simulation analysis of methane emissions from Irish agriculture
    1. S Hynes
    2. C O’Donoghue
    3. K Morrissey
    4. G Clarke
    (2009)
    Ecological Complexity 6:135–146.
    https://doi.org/10.1016/j.ecocom.2008.10.014
  24. 24
    Building a Static Farm Level Spatial Microsimulation Model: Statistically Matching the Irish National Farm Survey to the Irish Census of Agriculture
    1. S Hynes
    2. K Morrissey
    3. C O’Donoghue
    (2006)
    46th Congress of the European Regional Science Association.
  25. 25
    Package sms
    1. D Kavroudakis
    (2013)
    Accessed February 28, 2014.
  26. 26
    The regional impact of housing costs and assistance on financial disadvantage. AHURI Final Report No. 109
    1. J McNamara
    2. R Tanton
    3. B Phillips
    (2006)
    The regional impact of housing costs and assistance on financial disadvantage. AHURI Final Report No. 109.
  27. 27
    An Evaluation of Synthetic Household Populations for Census Collection Districts Created Using Spatial Microsimulation Techniques
    1. A Melhuish
    2. M Blake
    3. S Day
    (2002)
    Paper prepared for the 26th Australia & New Zealand Regional Science Association International (ANZRSAI) Annual Conference.
  28. 28
    Poverty at the Local Level: National and Small Area Poverty Estimates by Family Type for Australia in 2006
    1. R Miranti
    2. J McNamara
    3. R Tanton
    4. A Harding
    (2010)
    Applied Spatial Analysis and Policy 4:145–171.
    https://doi.org/10.1007/s12061-010-9049-1
  29. 29
    Small Area Estimates of Subjective Wellbeing : Spatial Microsimulation on the Australian Unity Wellbeing Index Survey. NATSEM Working Paper 13/23
    1. I Mohanty
    2. Y Tanton
    3. Y Vidyattama
    4. M Keegan
    5. R Cummins
    (2013)
    NATSEM, Canberra.
  30. 30
    The Life-Cycle Income Analysis Model (LIAM): A Study of a Flexible Dynamic Microsimulation Modelling Computing Framework
    1. C O’Donoghue
    2. J Lennon
    3. S Hynes
    (2009)
    International Journal of Microsimulation 2:16–31.
  31. 31
    Small Area Estimation-New Developments and Directions
    1. D Pfeffermann
    (2002)
    International Statistical Review 70:125–143.
    https://doi.org/10.1111/j.1751-5823.2002.tb00352.x
  32. 32
    Housing Stress Today : Estimates for Statistical Local Areas in 2005
    1. B Phillips
    2. S Chin
    3. A Harding
    (2006)
    Australian Consortium for Social and Political Research Incorporated Conference. pp. 10–13.
  33. 33
    Micro-level analysis of childhood obesity, diet, physical activity, residential socioeconomic and social capital variables: where are the obesogenic environments in Leeds?
    1. K Procter
    2. G Clarke
    3. J Ransley
    4. J Cade
    (2008)
    323–340, 40, 3, 10.1111/j.1475-4762.2008.00822.x.
  34. 34
    Economic-Demographic Effects of Immigration: Results from a Dynamic Spatial Microsimulation Model
    1. T Rephann
    (2004)
    International Regional Science Review 27:379–410.
    https://doi.org/10.1177/0160017604267628
  35. 35
    Understanding calibration estimators in survey sampling
    1. A Singh
    2. C Mohl
    (1996)
    Survey Methodology 22:107–115.
  36. 36
    Spatial microsimulation as a method for estimating different poverty rates in Australia
    1. R Tanton
    (2011)
    Population, Space and Place 17:222–235.
    https://doi.org/10.1002/psp.601
  37. 37
    Spatial Microsimulation: A Reference Guide for Users
    1. Tanton
    2. Edwards
    (editors) (2013)
    Netherlands: Springer.
  38. 38
    Urban and Rural Estimates of Poverty: Recent Advances in Spatial Microsimulation in Australia
    1. R Tanton
    2. A Harding
    3. J McNamara
    (2010)
    Geographical Research 48:52–64.
    https://doi.org/10.1111/j.1745-5871.2009.00615.x
  39. 39
    Pushing it to the edge: An assessment of spatial microsimulation methods
    1. R Tanton
    2. Y Vidyattama
    (2010)
    International Journal of Microsimulation 3:23–33.
  40. 40
    Old, Single and Poor: Using Microsimulation and Microdata to Analyse Poverty and the Impact of Policy Change among Older Australians. Economic Papers: A journal of applied economics and policy
    1. R Tanton
    2. Y Vidyattama
    3. J McNamara
    4. Q Vu
    5. A Harding
    (2009)
    102–120, Old, Single and Poor: Using Microsimulation and Microdata to Analyse Poverty and the Impact of Policy Change among Older Australians. Economic Papers: A journal of applied economics and policy, 28, 2, 10.1111/j.1759-3441.2009.00022.x%20.
  41. 41
    Small area estimation using a reweighting algorithm
    1. R Tanton
    2. Y Vidyattama
    3. B Nepal
    4. J McNamara
    (2011)
    Journal of the Royal Statistical Society: Series A (Statistics in Society 174:931–951.
    https://doi.org/10.1111/j.1467-985X.2011.00690.x
  42. 42
    Comparing two methods of reweighting a survey file to small area data: generalised regression and combinatorial optimisation
    1. R Tanton
    2. P Williamson
    3. A Harding
    (2014)
    International Journal of Microsimulation 7:76–99.
  43. 43
    Building a spatial microsimulation model’ Paper presented at the 11th European Colloquium on Quantitative and Theoretical Geography in Durham, England, on September 3–7, 1999
    1. Rephann Vencatasawmy
    2. Swan Esko
    3. Åström Öhman
    4. Holme Alfredsson
    5. Siikavaara
    (1999)
    Building a spatial microsimulation model’ Paper presented at the 11th European Colloquium on Quantitative and Theoretical Geography in Durham, England, on September 3–7, 1999.
  44. 44
  45. 45
    Small Area Social Indicators for the Indigenous Population: Synthetic Data Methodology for Creating Small Area Estimates of Indigenous Disadvantage. NATSEM Working Paper 13/24
    1. Y Vidyattama
    2. N Biddle
    3. R Tanton
    (2013)
    Canberra: NATSEM.
  46. 46
    Modelling the impact of declining Australian terms of trade on the spatial distribution of income
    1. Y Vidyattama
    2. M Rao
    3. I Mohanty
    4. R Tanton
    (2014)
    International Journal of Microsimulation 7:100–126.
  47. 47
    An evaluation of the combinatorial optimisation approach to the creation of synthetic microdata
    1. D Voas
    2. P Williamson
    (2000)
    International Journal of Population Geography 6:349–366.
  48. 48
    The distributional impact of the Australian Government’s Household Stimulus Package
    1. Q Vu
    2. R Tanton
    (2010)
    Australian Journal of Regional Studies 16:127–145.
  49. 49
    Community Care policies for the Elderly, 1981 and 1991: a microsimulation approach
    1. P Williamson
    (1996)
    In: G Clarke, editors. Microsimulation for Urban and Regional Policy Analysis. Pion Ltd. pp. 64–87.
  50. 50
    CO Instruction Manual
    1. P Williamson
    (2007)
    Population Microdata Unit, Dept. of Geography, University of Liverpool.
  51. 51
    The estimation of population microdata by using data from small area statistics and samples of anonymised records
    1. P Williamson
    2. M Birkin
    3. P Rees
    (1998)
    Environment and Planning A 30:785–816.
  52. 52
    Estimating small area demands for water with the use of microsimulation
    1. P Williamson
    2. G Clarke
    3. A McDonald
    (1996)
    In: G Clarke, editors. Microsimulation for Urban and Regional Policy Analysis. Pion Ltd. pp. 117–148.

Article and author information

Author details

  1. Robert Tanton

    National Centre for Social and Economic Modelling (NATSEM), Institute for Governance and Policy Analysis, University of Canberra, Australia
    For correspondence
    Robert.Tanton@canberra.edu.au

Publication history

  1. Version of Record published: April 30, 2014 (version 1)

Copyright

© 2014, Tanton

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Download citations (links to download the citations from this article in formats compatible with various reference manager tools)

Open citations (links to open the citations from this article in various online reference manager services)

Categories and tags