Comparing two methods of reweighting a survey file to small area data

Spatial microsimulation is a microsimulation method that can be used for small area estimation (Anderson, 2007; Clarke et al., 1997), projections (Williamson et al., 2002; Harding et al., 2011) and analysing small area policy change (Hynes et al., 2009; Tanton et al., 2009). Recent reviews of the field include Hermes and Poulsen (2012) and Tanton and Edwards (2013a). There are a number of methods that can be used for spatial microsimulation, and they have developed over a number of years. A brief review and history of the methods is described in a paper in this special issue (Tanton, 2014). There are also many applications of spatial microsimulation, and these are outlined in another paper in this special issue (O’Donoghue et al., 2014).

As far as the authors are aware, there have been two recent papers that have compared different spatial microsimulation methods (Williamson, 2013; Harland et al., 2012). This paper adds to this literature by comparing the generalised regression technique and the combinatorial optimisation technique. Both methods are described in Tanton and Edwards (2013b). The first uses a Generalised Regression (GREG) approach. GREG is a well-established approach to reweighting survey data (Lehtonen & Veijanen, 2009). The particular algorithm used in this paper iteratively attempts to minimise a truncated exponential distance function using a SAS program called GREGWT, developed by the Australian Bureau of Statistics from INSEE’s reweighting macro CALMAR (Bell, 2000). GREGWT is used by the ABS to benchmark their survey data to known State totals. The NATSEM adaptation of this approach to small-area estimation is documented in Tanton et al. (2011; 2013) and elaborated below in Sections 2 and 3 of this paper. The code for GREGWT is available on request from the ABS.

The second method of survey reweighting considered in this paper uses an iterative ‘combinatorial optimisation’ algorithm. An initial set (combination) of households are drawn from a survey at random (with replacement), following which a succession of random changes in the households selected are made, with a view to optimising the fit of the household combination to the specified small area benchmarks. To reduce the risk of getting trapped in a sub-optimal solution a simulated annealing approach to the acceptance of household changes is adopted. This algorithm is implemented using the program CO, developed by Dr Paul Williamson at the University of Liverpool (Williamson, 2007, 2013; Williamson, et al., 1998) and now available as part of an R library (Kavroudakis, 2013).

Unless earlier exit criteria are met (convergence measures for GREGWT; estimate fit thresholds for CO), both algorithms continue until a maximum number of user-specified iterations has been exceeded.

This paper compares the two algorithms in terms of their advantages and disadvantages for small-area estimation, including the number of areas which fail to satisfy minimum fit criteria, and the resulting weights from each method.

Section two of this paper outlines the data and benchmarks used for both methods. The data and benchmarks used for each method are exactly the same. Section three summarises the differences between the two methods, in terms of the methods and assumptions. Section four compares the results from each method, looking at the total difference and differences for each benchmark. Section 5 provides further analysis of the weights – including looking at the distribution of the weights from each procedure – while Section 6 provides conclusions and directions for further work.

There has been considerable work in Australia and Britain on generating small area estimates using survey data. The attraction of small area models is that they allow a survey designed for generating reliable estimates for a large area to be used to derive reliable estimates for a small area, without increasing the sample size, which is an expensive process.

In 2006, the Australian Bureau of Statistics (ABS) produced a small area estimation practice manual (ABS, 2006), which outlines some of the available techniques, and includes a section on diagnostics and quality measurement. The manual covers simple small area methods, like broad Area Ratio Estimator and Calibration estimators; and then covers regression methods, including random effects regression models. While this manual is theoretical, the ABS has also produced a number of small area estimates using a variety of techniques. Similar reviews have been compiled by, amongst others, Pfeffermann (2002), a consortium of European Statistical Agencies (EURAREA, 2005) and Marshall (2010).

In 2005, the ABS produced small area estimates of disability (ABS, 2005), which looked at three different methods of estimating disability for small areas; a Poisson regression model; a Bernoulli model; and ratio estimation. The report found that the Bernoulli model and the ratio estimator gave the best results, with the Poisson model performing poorly, possibly due to overdispersion.

The ABS also used a number of methods to generate small area estimates of crime. While some of this was unpublished, a method using a regression estimator was published (Tanton, et al., 2001). The results for small area estimates of crime from a number of other methods, including a ratio method based on an article by Purcell and Lincare (Purcell & Linacre, 1976) and a Structure Preserving Regression Estimator (SPREE) used for estimating labour force by the ABS, were unpublished, due to the fact that the results were difficult to validate.

This has been the biggest difficulty with the modelled small area estimates derived by the ABS – there is no estimate of the reliability of the results, for example, standard errors or confidence intervals. Recent work by the ABS has focussed on modelling labour force status, and assessing the quality of the estimates using relative root mean squared errors (RRMSEs) (ABS, 2011).

Outside of the ABS, the Australian Commonwealth Department of Employment and Workplace Relations uses a SPREE approach to estimate small area labour force statistics (Commonwealth Department of Employment and Workplace Relations, 2007). The ABS is now re-examining the estimation of the labour force using small area estimation techniques (ABS, 2012).

The National Centre for Social and Economic Modelling has also produced small area estimates of poverty and housing stress, using the methods outlined in this paper (see Harding, et al., 2006; Tanton et al., 2009; Tanton, 2011; Phillips, et al., 2006).

In the UK the Office for National Statistics has conducted a review of alternative methods for updating small area population estimates between censuses, in lieu of a population register, concluding by favouring a ratio change approach (Bates, 2006). An allied initiative has seen the development of small area estimates using a multilevel regression-based synthetic estimator fitted using area-level covariates. The result has been the release of a series of ‘experimental’ small-area statistics covering topics such as household overcrowding and social capital (Heady, et al., 2003), leading to the development of a regular series of official small area income estimates (Bond & Campos, 2010).

There are a number of theoretical differences between GREGWT and CO that need to be outlined.

This section shows summary results from the estimates produced by GREGWT and CO for the 307 SLAs in the ACT (the Australian Capital Territory) and NSW (New South Wales). NSW contains a range of urban and rural SLAs fairly representative of Australia as a whole, whilst the ACT contains some SLAs which are highly atypical in an Australian context, containing high concentrations of professionals and students. Results from GREGWT exlclude the 14% of SLAs classified, as per Section 3.1, as ‘non-convergent’. These non-convergent SLAs are predominantly less populous SLAs drawn from the industrial and remote areas of the ACT and NSW. Only 4.5% of the ACT population were in non-converging areas, and 4.6% of the NSW population.

The first set of results we consider here show how well each method has hit the benchmarks specified. The second set of results, more interestingly, show the usefulness of each method for predicting values not present in the benchmarks.

Predicting the benchmarks (constrained variables) is of limited interest, as by definition we already know their values. On the other hand, the difference between the estimated (weighted survey) and observed (census) values does at least provide some initial indicator of estimate quality. More usefully, the weighted data also yield estimates for unbenchmarked values. Two kinds of value-added estimates may be identified. The first involves the unbenchmarked interactions between benchmarked variables (margin constrained estimates). The second involves the unbenchmarked interactions between unbenchmarked variables (unconstrained estimates). The greater the degree of correlation between the benchmark constraints and the unbenchmarked estimates, the greater the quality of the estimate is likely to be. In constrast, values estimated using unbenchmarked variables that have no correlation with the benchmarked variables will necessarily be highly unreliable.

In this paper we evaluate the efficacy of our small area estimates in predicting housing stress. Housing stress is directly correlated with three of our constrained variables: income, rent paid and mortgage paid. A household is defined here as being in housing stress when they spend more than 30 per cent of their gross income on rent or a housing loan (a definition that can be matched from the ABS Census data so it can be validated against reliable small area data).

The average SLA-level fit to the benchmarks listed in Table 1 is summarised in Tables 4 and 5 for two States in Australia, New South Wales and the Australian Capital Territory, using a range of summary statistical measures described in Table 3. There are 107 areas estimated in the Australian Capital Territory and 199 in New South Wales. The SLAs in the ACT are atypical for Australia, both in terms of socio-demographic composition and in terms of size (ACT SLAs contain considerably fewer people than the average Australian SLA). The SLAs in NSW may be regarded as more ‘typical’ Australian SLAs.

The results are shown in Table 4 and Table 5, averaged across the SLAs for which GREGWT produced ‘convergent’ estimates.

Both variants of CO produced a better proportional fit to the estimation benchmarks than GREGWT (lower ORSumZ2 and OTAPE) but performed more variably when it came to matching GREGWT’s absolute fit to the estimation benchmarks. Of the two CO variants, CO (Min Proportion) unsurprisingly produced by far the lowest proportional error for both States; more surprisingly it also produced the lowest absolute error in NSW. This may reflect the fact that the SLAs in NSW are more populous, making the link between absolute and proportional values more tenuous. Overall the evidence presented in Tables 4 and 5 suggests a performance advantage favouring selection of CO (Min Proportion) over CO (Min Absolute), if such a choice has to be made.

As mentioned above, the main use for these reweighting techniques is to get estimates for variables that were not on the Census. We should be able to get reasonable estimates for variables that are correlated with the benchmarked variables (margin-constrained variables). For this paper, we calculated estimates of housing stress, which are correlated with some of the benchmarked variables (Income and Housing costs). Estimates of housing stress supplied by the Australian Bureau of Statistics from Census data provide an independent source against which to compare our own estimates.

A comparison of our various modelled estimates with those supplied by the ABS is presented in Table 6 for the Australian Capital Territory and New South Wales. It can be seen that all the models produced reasonable estimates of proportions, with the GREGWT estimates coming closest to the actual ABS per cent figures.

In terms of the number of people in housing stress, Table 6 appears to suggest that neither GREGWT nor CO estimate absolute numbers all that well. However, in considering Table 6 it should be borne in mind that the population base for the independent ABS housing stress estimates includes only households providing full returns on income and housing costs via their Census form. In contrast, the GREGWT and CO estimates have been weighted to fit benchmarks in which non-response households have been included via pro rating (see Section 3). Given that pro rating should more or less preserve the proportional distribution of households by income and housing cost, and given that the CO and GREGWT estimates closely replicate ABS estimates of the proportion of households in housing stress, it could in fact be argued that it is actually the ABS absolute estimates that are out of line. In any case, it is certainly true that GREGWT and CO outputs do need to be recognised as modelled estimates. As such, estimated proportions are more likely to be accurate than estimated levels – and so results are best presented as proportions or grouped into quantiles.

Another way of looking at these results is to look at the correlation between the different methods for each SLA in the area. In many recent papers on spatial microsimulation, this has been done using the Standard Error around Identity (SEI) (Ballas et al., 2007; Edwards & Tanton, 2013). The advantage of the SEI is that it provides a precise measure of the accuracy of the modelled estimates around reliable small area estimates.

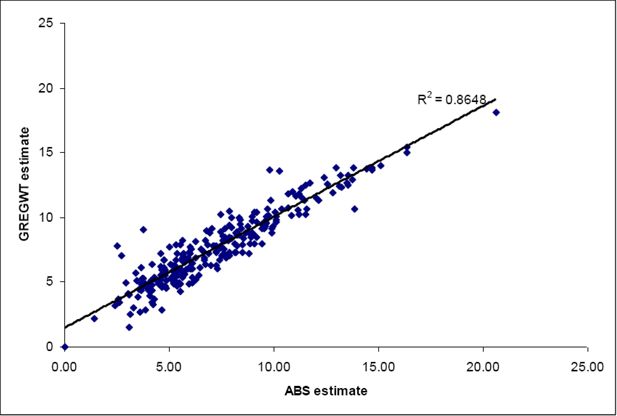
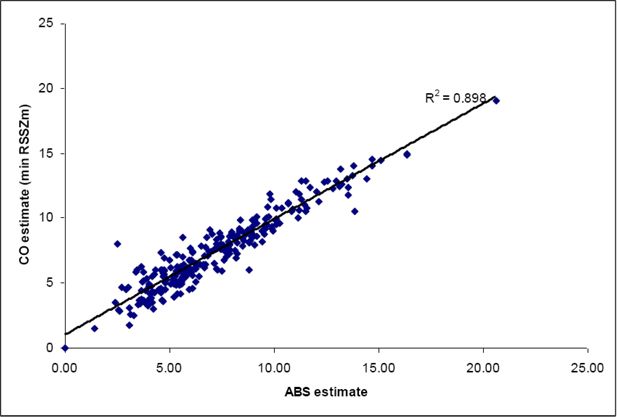
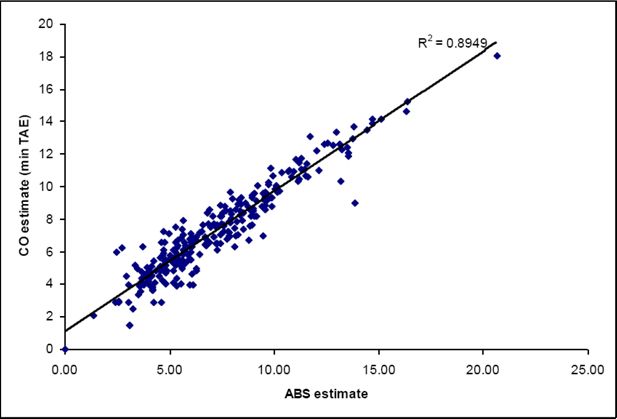
In this work, we have used a correlation coefficient rather than the SEI. The reason for this was twofold. The first was that the SEI assumes a slope of 1. In all three of the estimate comparisons made here (Figures 1–3), the slope is less than 1. This means that the CO and GREGWT estimates are typically higher than the ABS estimates for low levels of housing stress; and vice versa for high levels of housing stress. The second was that the SEI assumes an intercept of 0. In all three graphs, the intercept is not 0, suggesting a consistent bias in our results that the SEI would treat as error.

This means there is some obvious bias in our estimates, and in these cases the coefficient of determination (R2) may be a better estimate of the accuracy of the estimates, because of the enforced 0 intercept and slope of 1 for the SEI. Recent work by Vidyattama et al. (2013) used both the R2 and the SEI to show up a slight bias in their estimates due to the different datasets used in the spatial microsimulation process.

The graphs below (Figures 1–3) show the correlations between the ABS estimate and the different estimation methods we have used for all convergent SLAs in the Australian Capital Territory and New South Wales. It can be seen that the correlations are all very high (0.86 – 0.89). The highest correlation (and therefore lowest error) is from using the CO-Min Proportion model. Clearly the ranking of the three model estimates depends upon the precise measure used. But overall all three approaches appear to have done a good job of estimating the unknown three-way interaction between income and tenure-specific housing cost, from which the final estimate of housing stress is derived.

Figure 1

Download asset Open asset

Figure 2

Download asset Open asset

Figure 3

Download asset Open asset

While Section 4 has shown that the results from estimating different variables using these two methods are similar, the weights derived by each method are quite different. The CO routine derives integer weights – whereas the GREGWT routine doesn’t. We also expect more zero weights from the CO routine than we get using GREGWT. This section looks at the distribution of these weights.

The number of weights derived by each routine is massive. There are 6,892 households on our survey file that we derive weights for. In the Australian Capital Territory, there are 107 SLAs. So in the dataset of weights for the Australian Capital Territory, there are a total of about 740,000 weights calculated. For New South Wales, with 199 areas, there are about 1.4 million weights calculated.

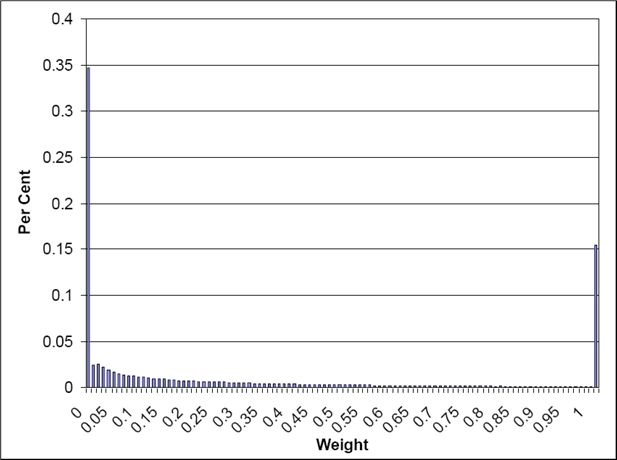
Table 7 shows the size distribution of the weights from CO and GREGWT. The CO routine only uses integer weights, so if there are fewer households in an SLA than in a survey, there will inevitably be survey households with a weight of 0. In contrast, GREGWT shares out the weights in small fractions across a large number of households. It can be seen, therefore, that the CO routine produces many more 0 weights than GREGWT.

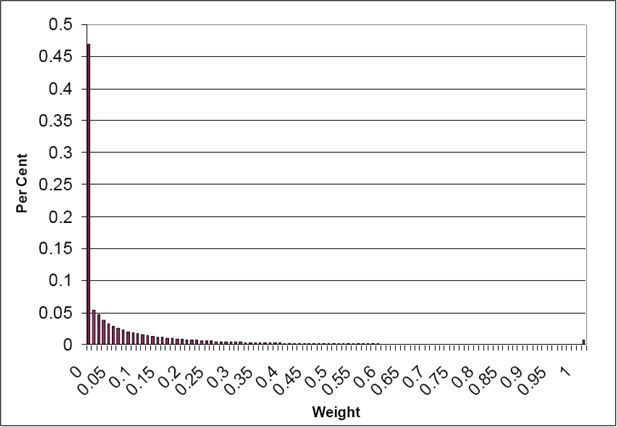
This also means that the CO routine is relying on fewer households to calculate the values of housing stress in the previous example. The GREGWT routine will use more households, with lower weights. The distribution of the weights from GREGWT for the Australian Capital Territory and New South Wales is shown in Figure 4 and Figure 5. Both these frequency distributions have class boundaries increasing by 0.01 until the value of one is reached, and the final category is weights greater than one. It can be seen that most of the weights in the Australian Capital Territory are below one (99 per cent of them, according to Table 7); in New South Wales, about 15 per cent are above one, but of these, half of them are under 2.

Figure 4

Download asset Open asset

Figure 5

Download asset Open asset

Frequency distributions have not been shown for the CO routine, as 95 per cent of the weights are 0 for each State, so the frequency distributions are dominated by this.

The other interesting statistic to look at with the weights is the maximum and average weights. For the GREGWT routine, non-convergence can lead to weights that are ridiculously large (in the order of 100,000 or more). Those areas where non-convergence occurs are usually less populous areas in the Northern Territory and West Australia, or industrial areas in cities where few people live. This is the case in the ACT and NSW.

One solution to the convergence issue is to reduce the number of benchmarks, or aggregate the benchmarks differently. Reducing the number of benchmarks is now standard in the SpatialMSM model to derive estimates for more areas, but this also affects the accuracy of the estimates, as with fewer benchmarks the estimates become less accurate against the benchmarked Census data. To enable consistency across all our areas estimated using SpatialMSM, we have not reduced the number of benchmarks or aggregated them differently in this analysis.

Excluding SLAs for which GREGWT produced non-convergent estimates, the maximum and average weights produced by GREGWT and CO are shown in Table 8. It can be seen that the CO routine produces a higher maximum for the Australian Capital Territory – but GREGWT produces a higher maximum for New South Wales.

The average values shown in Table 8 are calculated without zeroes, as there are so many in each procedure that they dominate an average. The values in Table 8 show that the CO routine calculates higher weights on average than the GREGWT routine for both New South Wales and the Australian Capital Territory. This is to be expected, given the number of zero weights calculated by the CO routine. To get to the same population in an area, the positive weights must be higher in the CO routine than the GREGWT routine, which has fewer zero weights.

This section has shown that even though the weights from the CO and GREGWT algorithm give similar results when calculating variables like housing stress, they are actually very different. The CO routine tends to include fewer households, but give them higher weights — while the GREGWT routine will select more households to represent an SLA, but will give them smaller weights.

The GREGWT algorithm has been shown to be capable of producing good results, but 14% of the total number of SLAs did not converge. These areas are industrial areas and remote areas in the ACT and NSW, and are usually less populous areas. Only 4.5% of the ACT population were in non-converging areas, and 4.6% of the NSW population.

The GREGWT algorithm also takes a long time to run compared to CO, particularly when estimating a large number of areas. It is unknown whether this is due to the programming language being used for each algorithm (CO uses a compiled FORTRAN code, whereas GREGWT is a macro running in SAS) or whether this reflects the relative efficiencies of the underlying algorithms.

Head-to-head, when results are compared for those SLAs for which GREGWT converged, the fit to benchmarks and estimates of housing stress produced by GREGWT and CO (Min Proportion) are broadly comparable. On balance, however, the CO Min Proportion model is perhaps slightly to be favoured. It has a better proportional fit to benchmarks (Table 4), the lowest error when estimating each SLA’s value (Figure 2), and produces reasonable estimates when the SLA values were aggregated to State (see Table 6). In addition, for those SLAs for which GREGWT produces no usable estimate, CO (Min Proportion) appears to continue to produce estimates of reasonable quality. CO (Min Absolute) competes slightly less well head to head with GREGWT, and in almost all circumstances produces estimates of at least marginally lesser quality than those offered by CO (Min Proportion).

1. 1
   Small area estimates of Disability in Australia

   1. ABS

   (2005)

   Canberra: ABS.

   • Google Scholar
2. 2
   A guide to small area estimation - Version 1.0

   1. ABS

   (2006)

   A guide to small area estimation - Version 1.0, http://www.nss.gov.au/nss/home.NSF/533222ebfd5ac03aca25711000044c9e/3a60738d0abd f98cca2571ab00242664/$FILE/May%2006.pdf, accessed 19 May 2014.

   • Google Scholar
3. 3
   Time series

   1. ABS

   (2012)

   5673.0.55.003, Time series, ABS, Canberra.

   • Google Scholar
4. 4
   Small Area Estimation with Simulated Samples from the Population Census. Cat # 1352.0.55.106

   1. ABS

   (2011)

   Canberra: ABS.

   • Google Scholar
5. 5
   Creating Small-Area Income Estimates: Spatial Microsimulation Modelling

   1. B Anderson

   (2007)

   UK Department of Communities. Accessed February 21, 2014.
6. 6
   Using SimBritain to Model the Geographical Impact of National Government Policies

   1. Clarke Ballas
   2. Dorling
   3. Rossiter

   (2007)

   Geographical Analysis 39:44–77.

   • Google Scholar
7. 7
   Methodology used for producing ONS’s small area population estimates

   1. A Bates

   (2006)

   Population Trends 125:30–36.

   • Google Scholar
8. 8
   GREGWT and TABLE macros - Users guide

   1. P Bell

   (2000)

   Canberra: ABS, Unpublished.

   • Google Scholar
9. 9
   ‘Understanding income at small area level’, Regional Trends 42: 2010 edition

   1. S Bond
   2. C Campos

   (2010)

   London: Office for National Statistics.

   • Google Scholar
10. 10
    Spatial Microsimulation : Preparation of Sample Survey and Census Data for SpatialMSM / 08 and SpatialMSM/09. NATSEM Technical Paper 36, NATSEM

    1. R Cassells
    2. A Harding
    3. R Miranti
    4. R Tanton
    5. J Mcnamara

    (2010)

    Spatial Microsimulation : Preparation of Sample Survey and Census Data for SpatialMSM / 08 and SpatialMSM/09. NATSEM Technical Paper 36, NATSEM.

    • Google Scholar
11. 11
    Building a static spatial microsimulation model: Data preparation

    1. R Cassells
    2. R Miranti
    3. A Harding

    (2013)

    In: R Tanton, K Edwards, editors. Spatial Microsimulation: A Reference Guide for Users. Netherlands: Springer. pp. 87–103.

    • Google Scholar
12. 12
    Regional dimensions: Preparation of 1998-99 HES for reweighting to small area benchmarks. Technical Paper 34, NATSEM

    1. S-F Chin
    2. A Harding
    3. A Bill

    (2006)

    Regional dimensions: Preparation of 1998-99 HES for reweighting to small area benchmarks. Technical Paper 34, NATSEM.

    • Google Scholar
13. 13
    Estimating Small Area Demand for Water: A New Methodology

    1. G Clarke
    2. A Kashti
    3. A McDonald
    4. P Williamson

    (1997)

    Water and Environment Journal 11:186–192.

    • Google Scholar
14. 14
    Small Area Labour Markets

    1. Commonwealth Department of Employment and Workplace Relations

    (2007)

    Commonwealth Government.

    • Google Scholar
15. 15
    Validation of Spatial Microsimulation Models

    1. and Edwards
    2. Tanton

    (2013)

    In: Tanton, Edwards, editors. Spatial Microsimulation: A Reference Guide for Users. Springer. pp. 249–258.

    • Google Scholar
16. 16
    Enhancing Small Area Estimation Techniques to meet European Needs

    1. EURAREA

    (2005)

    Project Reference Volume, The EURAREA Consortium.

    • Google Scholar
17. 17
    Assessing poverty and inequality at a detailed regional level: New advances in spatial microsimulation

    1. A Harding
    2. R Lloyd
    3. A Bill
    4. A King

    (2006)

    Helsinki: United Nations University Press.

    • Google Scholar
18. 18
    Demographic Change and the Needs-Based Planning of Government Services: Projecting Small Area Populations Using Spatial Microsimulation

    1. A Harding
    2. Y Vidyattama
    3. R Tanton

    (2011)

    Journal of Population Research 28:203–224.

    • Google Scholar
19. 19
    Creating Realistic Synthetic Populations at Varying Spatial Scales: A Comparative Critique of Population Synthesis Techniques

    1. K Harland
    2. A Heppenstall
    3. D Smith
    4. M Birkin

    (2012)

    Journal of Artificial Societies and Social Simulation 15:1–24.

    • Google Scholar
20. 20
    Model-Based Small Area Estimation Series No. 2 - Small Area Estimation Project Report

    1. P Heady
    2. P Clarke
    3. G Brown
    4. K Ellis
    5. D Heasman
    6. S Hennell
    7. J Longhurst
    8. B Mitchell

    (2003)

    Office of National Statistics.

    • Google Scholar
21. 21
    A Review of Current Methods to Generate Synthetic Spatial Microdata Using Reweighting and Future Directions

    1. K Hermes
    2. M Poulsen

    (2012)

    Computers, Environment and Urban Systems 36:281–290.

    • Google Scholar
22. 22
    A Spatial Micro-Simulation Analysis of Methane Emissions from Irish Agriculture

    1. S Hynes
    2. C O’Donoghue
    3. K Morrissey
    4. G Clarke

    (2009)

    Ecological Complexity 6:135–146.

    • Google Scholar
23. 23
    sms: Spatial Microsimulation

    1. D Kavroudakis

    (2013)

    R Package, http://cran.r-project.org/web/packages/sms/index.html.

    • Google Scholar
24. 24
    Design-based methods of estimation for domains and small areas

    1. R Lehtonen
    2. A Veijanen

    (2009)

    Design-based methods of estimation for domains and small areas, Handbook of statistics, 29, B, Sample surveys: theory, methods and inference, Elsevier.

    • Google Scholar
25. 25
    ESDS Government, Economic and Social Data Service

    1. A Marshall

    (2010)

    ESDS Government, Economic and Social Data Service, University of Essex.

    • Google Scholar
26. 26
    Spatial Microsimulation Modelling: a Review of Applications and Methodological Choices

    1. C O’Donoghue
    2. K Morrissey
    3. J Lennon

    (2014)

    International Journal of Microsimulation 7:26–75.

    • Google Scholar
27. 27
    Small area estimation – new developments and directions

    1. D Pfefferman

    (2002)

    International Statistical Review 70:125–143.

    • Google Scholar
28. 28
    Housing Stress Today: Estimates for Statistical Local Areas in 2005

    1. B Phillips
    2. SF Chin
    3. A Harding

    (2006)

    Paper given at Australian Consortium for Social and Political Research Incorporated Conference. pp. 10–13.

    • Google Scholar
29. 29
    Techniques for the Estimation of Small Area Characteristics

    1. N Purcell
    2. S Linacre

    (1976)

    Paper given at Third Australian Statistical Conference.

    • Google Scholar
30. 30
    Understanding calibration estimators in survey sampling

    1. A Singh
    2. C Mohl

    (1996)

    Survey Methodology 22:107–115.

    • Google Scholar
31. 31
    Spatial microsimulation as a method for estimating different poverty rates in Australia

    1. R Tanton

    (2011)

    Population, Space and Place 17:222–235.

    • Google Scholar
32. 32
    A Review of Spatial Microsimulation Methods

    1. R Tanton

    (2014)

    International Journal of Microsimulation 7:4–25.

    • Google Scholar
33. 33
    Spatial Microsimulation: A Reference Guide for Users, Understanding Population Trends and Processes, 6

    1. R Tanton
    2. KL Edwards

    (2013a)

    Netherlands: Springer.

    • Google Scholar
34. 34
    Introduction to Spatial Microsimulation: History, Methods and Applications

    1. R Tanton
    2. KL Edwards

    (2013b)

    In: R Tanton, K Edwards, editors. Spatial Microsimulation: A Reference Guide for Users. Netherlands: Springer. pp. 3–8.

    • Google Scholar
35. 35
    Spatial Microsimulation Using a Generalised Regression Model

    1. R Tanton
    2. A Harding
    3. J McNamara

    (2013)

    In: R Tanton, K Edwards, editors. Spatial Microsimulation: A Reference Guide for Users. Netherlands: Springer. pp. 87–103.

    • Google Scholar
36. 36
    Small Area Poverty Estimates for Australia’s Eastern Seaboard in 2006

    1. R Tanton
    2. J McNamara
    3. A Harding
    4. T Morrison

    (2009)

    In: A Harding, A Zaidi, editors. New Frontiers in Microsimulation Modelling. Vienna, Austria: Ashgate. pp. 79–97.

    • Google Scholar
37. 37
    Old, Single and Poor: Using Microsimulation and Microdata to Analyse Poverty and the Impact of Policy Change among Older Australians

    1. R Tanton
    2. Y Vidyattama
    3. J McNamara
    4. Q Vu
    5. A Harding

    (2009)

    Economic Papers: A Journal of Applied Economics and Policy 28:102–120.

    • Google Scholar
38. 38
    Small area estimation using a reweighting algorithm

    1. R Tanton
    2. Y Vidyattama
    3. B Nepal
    4. J McNamara

    (2011)

    Journal of the Royal Statistical Society: Series A (Statistics in Society 174:931–951.

    • Google Scholar
39. 39
    Analyses of the 1998 Australian National Crime and Safety Survey

    1. R Tanton
    2. R Jones
    3. G Lubulwa

    (2001)

    Paper given at The Character, Impact and Prevention of Crime in Regional Australia, Townsville, 2–3 August 2001.

    • Google Scholar
40. 40
    The Challenges of Combining Two Databases in Small-Area Estimation: An Example Using Spatial Microsimulation of Child Poverty

    1. Y Vidyattama
    2. J McNamara
    3. R Miranti
    4. R Tanton
    5. A Harding

    (2013)

    Environment and Planning A 45:344–361.

    • Google Scholar
41. 41
    Evaluating goodness-of-fit measures for synthetic microdata

    1. D Voas
    2. P Williamson

    (2001)

    Geographical and Environmental Modelling 5:177–200.

    • Google Scholar
42. 42
    CO Instruction Manual, Working Paper 2007/1

    1. P Williamson

    (2007)

    Population Micordata Unit, Dept. of Geography, University of Liverpool.

    • Google Scholar
43. 43
    An Evaluation of Two Synthetic Small-Area Microdata Simulation Methodologies: Synthetic Reconstruction and Combinatorial Optimisation

    1. P Williamson

    (2013)

    In: R Tanton, K Edwards, editors. Spatial Microsimulation: A Reference Guide for Users. Netherlands: Springer. pp. 19–47.

    • Google Scholar
44. 44
    The estimation of population microdata by using data from small area statistics and samples of anonymised records

    1. P Williamson
    2. M Birkin
    3. P Rees

    (1998)

    Environment and Planning A 30:785–816.

    • Google Scholar
45. 45
    Domestic Water Demand Forecasting: A Static Microsimulation Approach

    1. P Williamson
    2. G Mitchell
    3. A McDonald

    (2002)

    Water and Environment Journal 16:243–248.

    • Google Scholar

Author details

1. Robert Tanton

   National Centre for Social and Economic Modelling (NATSEM), Institute for Governance and Policy Analysis, University of Canberra, Australia

   For correspondence

   robert.tanton@canberra.edu.au

2. Paul Williamson

   Department of Geography and Planning, University of Liverpool, United Kingdom

   For correspondence

   P.Williamson@liv.ac.uk

3. Ann Harding

   National Centre for Social and Economic Modelling (NATSEM), Institute for Governance and Policy Analysis, University of Canberra, Australia

   For correspondence

   ann.harding@canberra.edu.au