
Coordination in centralized and decentralized systems
Abstract
We study a simple coordination problem to understand the difference between centralized and decentralized economic systems. The decentralized system is more robust than the centralized system to communication errors. But the centralized system takes less time than the decentralized system to create coordination among constituent parts. Decentralization is preferable when the constituent parts are more likely to make communication errors, when there is little urgency, and when there is need to prevent system-collapse.
1. Introduction
How does the structure of an economic system affect its performance? By “structure” we mean the way in which different constituent parts are related to each other in terms of communication and decision-making. Most economies have a complex mix of different structures including markets, firms, and government agencies of various kinds. Despite their differences, all these structures face the common problem of coordinating the activities of constituent parts who possess private information. There are two ways in which markets, firms, and government agencies solve coordination problems: centralization and decentralization. The Chicago Mercantile Exchange has a central clearing house and quotation system (Millo, Muniesa, Panourgias, & Scott, 2005), but Torino’s farmers market has no such central structure. Alfred Sloan granted considerable autonomy to division managers in General Motors (Sloan, 1964), but such autonomy does not exist in all firms (Love, Priem, & Lumpkin, 2002). The United States government consists of various federal, state, and local departments with overlapping jurisdictions (Liesbet & Gary, 2003). The North Korean government is presumably largely centrally organized with organs like the “Central People’s Committee” and the “State Planning Committee”. As to how the structure of an economic system affects its performance is a fundamental theoretical question with a bearing on the microstructure of markets, the internal organization of firms, and the structure of governments.
In this paper, we compare the performance of a centralized and a decentralized system in solving a simple coordination problem when their constituent parts make errors in communicating private information. We find that the decentralized system is more robust than the centralized system to communication errors. But the centralized system takes less time than the decentralized system to create coordination. Our analysis sheds light on the influence of communication technology on organizational forms, the greater variability of autocratic societies compared to democratic societies, the variation in economic organization with product type, and the preference for centralized organization in urgencies like war.
We study a simple ordering problem in which agents are indexed by a number and randomly placed on a line. The coordination problem is to order the agents according to their numbers, with the least numbered agent on left and highest numbered on the right. In the centralized system, agents communicate their numbers to a central authority, who uses the information to order the agents. In the decentralized system, agents communicate their numbers to neighbours and swap positions if the number of the agent on left is more than the number of the agent on right. Agents probabilistically make errors in communicating private information in the centralized system and the decentralized system. We find that the decentralized system is more robust to communication errors than the centralized system. This is because the centralized system of coordination involves a strong-dependence between the information communicated by constituent parts (Simon, 1962). Errors in the information communicated by one agent to the central-coordinator negatively affects the usefulness of the information communicated by other agents to the central-coordinator. The decentralized system on the other hand involves weak-dependence between the information communicated by constituent parts. Errors in the information communicated by one agent to its neighbour has a negligible effect on the usefulness of the information communicated by other agents to their neighbours. The localization of decision-making in the decentralized system limits the impact of communication errors on the system’s performance. The strong-dependence between the information communicated by different agents in the centralized system and the weak-dependence in the decentralized system is a consequence of the difference in structure of communication and decision-making in the two systems.
Von Neumann (1951) illustrates the idea of strong-dependence and weak-dependence with the following analogy. Imagine placing your hand in a tub of water at 80°C. There are two ways to communicate this information from the nerve endings in your hand to your brain. One way is to convey the temperature in binary form. Another way is the counting method, where one count is communicated for each 1°C. Interestingly, the human nervous system uses a mechanism roughly akin to the counting method. This despite the fact that the counting method involves communicating orders of magnitude more information than the binary method. Von Neumann (1951, p. 101) speculates on why the human nervous system uses the counting method: “...the counting method has a high stability and safety from error. If you express a number of the order of million by counting and miss a count, the result is only irrelevantly changed. If you express it by (decimal or binary) expansion, a single error in a single digit may vitiate the entire result.”
80°C in binary is 1010000. If the first digit is erroneously reported as 0, the temperature conveyed is 16°C. The usefulness of correct information conveyed by all other digits is vitiated by a single error. In contrast to the binary method, in the counting method the absence of a count has a negligible effect on the usefulness of the other counts. If a count is missed, the temperature conveyed is 79°C. There is strong-dependence among the digits in the binary method, but weak-dependence among the counts in the counting method. The principle of strong and weak dependence are at play in centralized and decentralized systems, and is the cause of the greater robustness of the decentralized system to communication errors.
Though the decentralized system is more robust to communication errors, the centralized system uses less time to create coordination. The absence of a central decision-making unit means that the decentralized system has to muddle through numerous local communications and decisions, all of which takes time. The very structural feature that makes the decentralized system robust also makes it slow. Centralization is preferable to decentralization when there is urgency and when constituent parts are less likely to make errors in communicating private information.
Our paper is related to the literature on the architecture of economic systems (Bolton & Farrell, 1990; Guerini, Napoletano, & Roventini, 2016; Hayek, 1945; Lange, 1936; Sah & Stiglitz, 1986), the literature on the internal organization of firms (Acemoglu, Aghion, Lelarge, van Reenen, & Zilibotti, 2007; Alonso, Dessein, & Matouschek, 2008; Maskin, Qian, & Xu, 2000; Stein, 2002), and the literature on the structure of governments (Egeberg, 2007; Landau, 1969; Peters, 1998). The literature on the architecture of economic systems began with the socialist calculation debate between Otto Neurath and Ludwig von Mises, though the modern strand originates from the contributions of Hayek and Lange. Hayek (1945) claimed the market system is superior to communist central planning in using dispersed information to coordinate the activities of different agents. Lange (1936) argued central planning can attain efficient allocation of resources by mimicking the price system. While the relative advantages of price, shadow-price, and non-price mechanisms of coordination are important, “there is more at stake in the choice of an economic system” (Sah & Stiglitz, 1986, p. 726). One of the differences between centralized and decentralized economic systems is how they perform in the presence of communication errors. The difference between the Soviet centrally planned economy and the US economy is not only one of the extent to which they use price signals to communicate economic information, but also the structures through which they communicate information. These structures influence the performance of the two systems when economic signals contain noise.
The question of the architecture of economic systems is not limited to understanding the differences between economic systems. It also pertains to understanding the differences in the mix of markets, firms, and government agencies within an economic system (Hall & Soskice, 2001). Our paper is a close cousin of Sah and Stiglitz (1986), Bolton and Farrell (1990), and Guerini et al. (2016). While we study the consequence of errors in the communication of information, Sah and Stiglitz (1986) study the consequence of errors in the processing of information in alternate economic arrangements. Bolton and Farrell (1990) study the problem of entry in a system with two agents with differing costs. Bolton and Farrell argue that decentralization involves duplication and delay. We too find decentralization involves delay, but for a reason different from Bolton and Farrell’s. In our model, the decentralized system takes more time than the centralized system because the decentralized system has to muddle through numerous local communications and decision-making. In Bolton and Farrell’s model, delay occurs because agents do not communicate with each other in the decentralized system. Guerini et al. (2016) study the macroeconomic performance of a centralized and a decentralized protocol of search and matching. They find that the centralized protocol produces full-employment, whereas the decentralized protocol produces unemployment. We believe their results may change if the coordinator in the centralized protocol has to collect private information from agents who make communication errors.
In the literature on the role of information in shaping the internal organization of firms, our paper is related to Stein (2002), Maskin et al. (2000), Acemoglu et al. (2007), and Alonso et al. (2008). Our paper shares some ingredients with these papers, while differing from them in important respects. In Stein (2002) model agents do not communicate private information in the decentralized system. In Acemoglu et al. (2007) model agents do not communicate private information in the centralized system. In contrast to Stein and Acemoglu et al., we study the differences in the performance of centralized and decentralized systems due to the differences in their structures of communication and decision-making. Maskin et al. (2000) and Alonso et al. (2008) study the differences in performances of systems because their structure influences the incentives to communicate private information. Our paper studies the differences in performance of systems even when their structures do not influence incentives. Matters other than incentives matter. All this means that even when our conclusions concur with those of other papers in the literature, the reasoning behind the conclusions differ. For instance, Stein (2002) concludes decentralization is preferable when information is difficult to communicate. This is similar to our conclusion that decentralization is preferable when there is a greater likelihood of communication errors. After all, information is difficult to communicate when there are communication errors. However, the reasoning behind Stein’s conclusion differs from ours. In Stein’s case, decentralization is preferable when information is difficult to communicate because no communication is necessary in the decentralized system. In our case, decentralization is preferable when information is difficult to communicate because the localization of communication limits the consequences of communication errors on the system’s performance. Our contribution to the literature on firms is that the internal structure of firms matters because it determines the robustness of firms to employees’ communication errors and the speed with which firms can coordinate the activities of its employees.
Our paper is also related to the literature on the structure and performance of governments (Bendor, Glazer, & Hammond, 2001; Ostrom, Tiebout, & Warren, 1961; Ostrom, 1999). Ostrom et al. (1961) argue that the presence of multiple government agencies with overlapping jurisdictions is not a pathological phenomenon, nor can the problems posed by the multiplicity of government agencies be resolved by centralization. The contribution by Ostrom et al. (1961) sparked an interesting literature on the origin and performance of alternate structures of government. This literature studied a variety of ways in which structure affects performance, including the relation between norms and governance structures (Ostrom, 1999), and the influence of government structure on incentives to truthfully reveal information (Bendor et al., 2001). Our analysis suggests that the structure of government influences performance, even when the structure does not influence social norms and incentives. Most governments have a rich and intricate framework for negotiation and adjudication between different agencies. Negotiation and adjudication involves error-prone communication. Our model suggests that the structure of government influences its robustness to error-prone communication between different agencies and the speed with which governments can execute tasks. Our paper is organized as follows. Section 2 presents the model. Section 3 reports and explains the results of the model. Section 4 discusses the implications of the ideas developed in this paper. Section 5 offers concluding remarks.
2. The model
Imagine a set of n agents numbered from 1 to n. No two agents have the same number. The agents are randomly placed on a line segment; they are in no particular order. The coordination problem is to order the agents from 1 to n from left to right, where each agent’s number is one greater than the number of its neighbour on the left and one less than the number of its neighbour on the right. The first agent does not have a left neighbour and the last agent does not have a right neighbour. There are two ways to order the agents: a centralized system and a decentralized system. In the centralized system, each agent conveys its number to a central-coordinator. The central-coordinator orders the agents on a line segment. For instance, if an agent communicates its number as 3, the central-coordinator places the agent in position 3 on the line segment. The central-coordinator orders the agents as the agents communicate their numbers to the central-coordinator. The decentralized system works differently. Each time step, pairs of neighbouring agents are randomly selected. Within each pair, agents share information about each other’s numbers. If the agent on the left reports a number greater than the agent on the right, the agents swap positions, otherwise the agents remain in their current positions. Over time, the agents incrementally order themselves.
Agents make errors in communicating their numbers, i.e. with some probability an agent conveys an incorrect number. When an agent makes a communication error, it reports a random number between 1 and n rather than its true number. Communication errors create problems in the centralized system and the decentralized system. In the centralized system, the central-coordinator places the agent who reports an incorrect number in an incorrect location. Further problems arise because another agent cannot be placed in that location. For instance, if agent 3 reports number 5 and is placed in location 5, agent 5 cannot be placed in location 5. When an agent reports a number whose location is occupied, the central-coordinator places it in the nearest empty location.
In the decentralized system, communication errors cause agents to wrongly swap positions, i.e. a greater number agent may move left and a lower number agent may move right. Suppose agent 3 and agent 5 are neighbours with agent 3 on the left of agent 5. Upon activation the agents communicate their numbers to each other. Agent 3 correctly communicates its number, but agent 5 makes an error and communicates 2 as its number. The two agents swap positions. Agent 5 moves left and agent 3 moves right, thereby decreasing the system’s coordination.
In the centralized system, at the first time step all n agents communicate their numbers to the central-coordinator. The central-coordinator orders the agents at the end of the first time step using the collected information. In the decentralized system, at each time step, n neighbouring pairs of agents are randomly activated. The activated agents exchange information and swap positions if necessary. In the decentralized system, agents incrementally order themselves over many time steps.
The coordination in the system is measured using the formula
where ai is the number of agent i and li is the number of the location of agent i. Coordination is the negative mean of the absolute value of the differences between the numbers of agents and the numbers of their respective locations. For instance, if agent 3 is at location 5, the absolute value of difference is 2. The sum of these differences is divided by the total number of agents and multiplied by negative one to measure coordination. Zero indicates perfect coordination, lower values of C indicate lesser coordination. The model is built in Python programming language. Model code is available at https://bitbucket.org/VipinVeetil/CoordinationSystems.
Section 3 reports the results from numerous simulations of the model. In each simulation, the centralized system is run for one time step because it orders the agents after the first time step. In each simulation, the decentralized system is run for 1,000 time steps, and its coordination is measured at the end of the last time step. Figures 1, 2, 3, and 4 report the results from 104 simulations of the centralized system and the decentralized system for each probability of error in the range [0, 1] with increments of 0.01. Therefore, Figures 1, 2, 3, and 4 summarize the results from 2 x 106 simulations. Figure 5 reports the results from 103 simulations of the centralized system and the decentralized system for each number of agents in the interval [10, 1000] with increments of 10. Therefore, Figure 5 summarizes the outcome of 2 x 105 simulations.
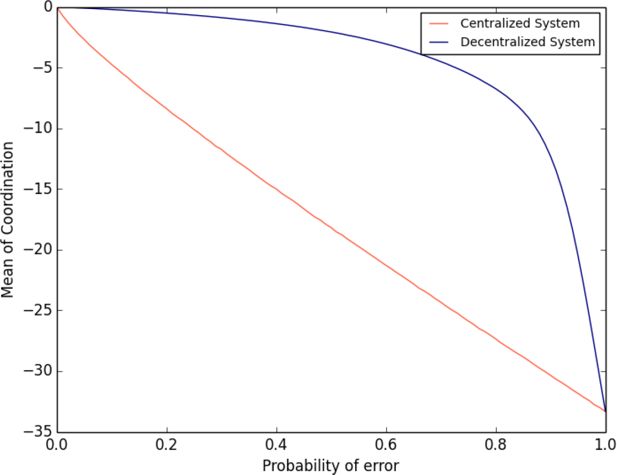
Mean of coordination in the centralized and the decentralized system.
Note: In the centralized system, each agent conveys its number to a central-coordinator. The central-coordinator orders the agents on a line segment. In the decentralized system, at each time step, pairs of neighbouring agents are randomly selected. Within each pair, agents share information about each other5 s numbers. If the agent on the left reports a number greater than the agent on the right, the agents swap positions, otherwise the agents remain in their present positions. Agents make errors in communicating their numbers, i.e. with some probability an agent conveys an incorrect number. Coordination is the negative mean of the absolute value of the differences between the numbers of agents and the numbers of their respective locations. The sum of these differences is divided by the total number of agents and multiplied by negative one to measure coordination. Zero indicates perfect coordination, lower values of C indicate lesser coordination.
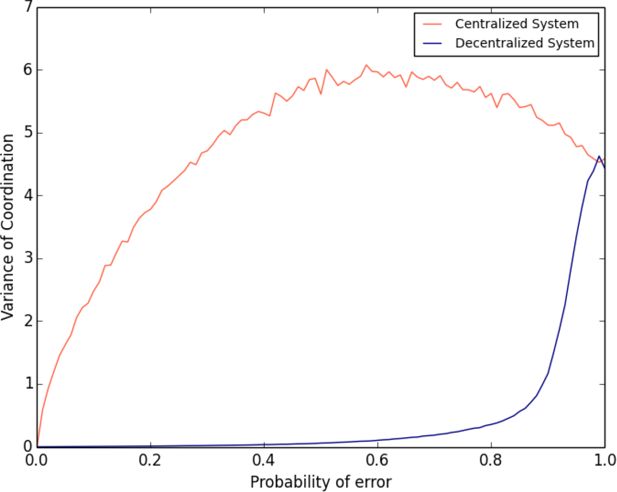
Variance of coordination in the centralized and the decentralized system.
Note: In the centralized system, each agent conveys its number to a central-coordinator. The central-coordinator orders the agents on a line segment. In the decentralized system, at each time step, pairs of neighbouring agents are randomly selected. Within each pair, agents share information about each other5 s numbers. If the agent on the left reports a number greater than the agent on the right, the agents swap positions, otherwise the agents remain in their present positions. Agents make errors in communicating their numbers, i.e. with some probability an agent conveys an incorrect number. Coordination is the negative mean of the absolute value of the differences between the numbers of agents and the numbers of their respective locations. The sum of these differences is divided by the total number of agents and multiplied by negative one to measure coordination. Zero indicates perfect coordination, lower values of C indicate lesser coordination.
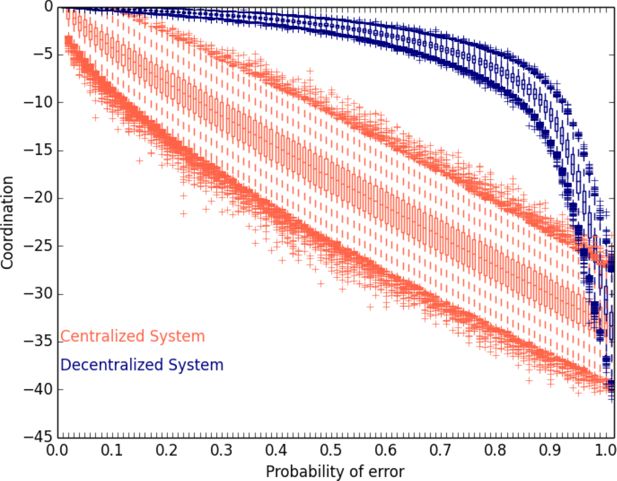
Boxplots of coordination in the centralized and the decentralized system.
Note: In the centralized system, each agent conveys its number to a central-coordinator. The central-coordinator orders the agents on a line segment. In the decentralized system, at each time step, pairs of neighbouring agents are randomly selected. Within each pair, agents share information about each other5 s numbers. If the agent on the left reports a number greater than the agent on the right, the agents swap positions, otherwise the agents remain in their present positions. Agents make errors in communicating their numbers, i.e. with some probability an agent conveys an incorrect number. Coordination is the negative mean of the absolute value of the differences between the numbers of agents and the numbers of their respective locations. The sum of these differences is divided by the total number of agents and multiplied by negative one to measure coordination. Zero indicates perfect coordination, lower values of C indicate lesser coordination.
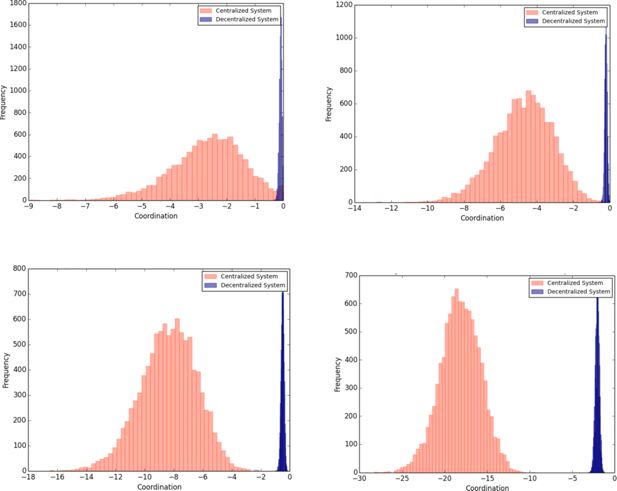
Histograms of coordination of the centralized and decentralized systems with different probabilities of error.
Note: In the centralized system, each agent conveys its number to a central-coordinator. The central-coordinator orders the agents on a line segment. In the decentralized system, at each time step, pairs of neighbouring agents are randomly selected. Within each pair, agents share information about each other5 s numbers. If the agent on the left reports a number greater than the agent on the right, the agents swap positions, otherwise the agents remain in their present positions. Agents make errors in communicating their numbers, i.e. with some probability an agent conveys an incorrect number. Coordination is the negative mean of the absolute value of the differences between the numbers of agents and the numbers of their respective locations. The sum of these differences is divided by the total number of agents and multiplied by negative one to measure coordination. Zero indicates perfect coordination, lower values of C indicate lesser coordination.
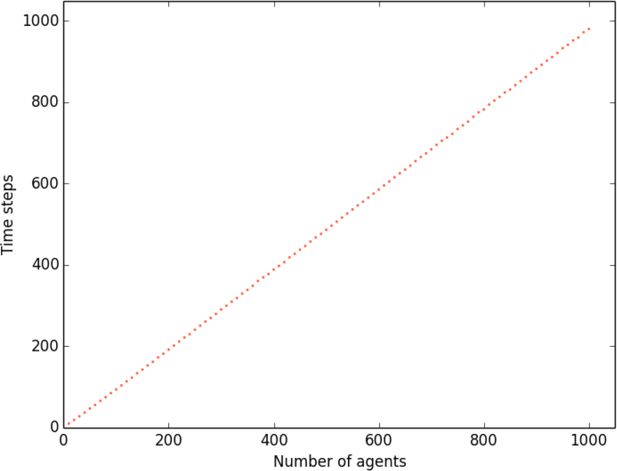
Time steps necessary for decentralized system to exceed the mean coordination of the centralized system with ten percent probability of communication error.
Note: In the centralized system, each agent conveys its number to a central-coordinator. The central-coordinator orders the agents on a line segment. In the decentralized system, at each time step, pairs of neighbouring agents are randomly selected. Within each pair, agents share information about each other5 s numbers. If the agent on the left reports a number greater than the agent on the right, the agents swap positions, otherwise the agents remain in their present positions. Agents make errors in communicating their numbers, i.e. with some probability an agent conveys an incorrect number. Coordination is the negative mean of the absolute value of the differences between the numbers of agents and the numbers of their respective locations. The sum of these differences is divided by the total number of agents and multiplied by negative one to measure coordination. Zero indicates perfect coordination, lower values of C indicate lesser coordination.
3. The model
Result 1 shows that the centralized system has lower mean coordination and a greater variance of coordination than the decentralized system. Figure 1 shows that the mean coordination of the centralized system is less than the mean of the decentralized system. Figure 2 shows that the variance of the coordination of the centralized system is greater than the variance in the decentralized system. Figure 3 presents box-plots using all the data points used to compute mean and variance plotted in Figures 1 and 2. Figure 4 plots histograms of the coordination of the centralized system and the decentralized system for four different probabilities of communication errors. Like Figures 1 and 2, Figures 3 and 4 show that the centralized system has a lower mean and a greater variance than the decentralized system.
The centralized system has a lower mean than the decentralized system for the following reason. In the centralized system, an individual agent’s communication error has a significant impact on the coordination created by the central-coordinator. One agent’s misplacement has the potential to produce a cascade of misplacements. Suppose agent 3 communicates number 5 and is placed at location 5. Agent 5 makes no communication error, but agent 5 cannot be placed in location 5 because location 5 is occupied by agent3. The central coordinator places agent5 at the nearest empty location, say location 7. This means agent 7 cannot be placed at location 7. Agent 3’s communication error has the potential to create the misplacements of other agents, even when other agents do not make communication errors. In the centralized system, the communication errors of some agents can vitiate the usefulness of correct information communicated by many agents. This is due to the very structure of ordering in the centralized system.
In contrast to the centralized system, in the decentralized system an individual agent’s communication error has a local impact; a lower number agent may move to the right of a higher number agent, thereby producing a minor decrease in the decentralized system’s coordination. In the decentralized system, the impact of an individual agent’s communication error on the system’s performance is limited. Suppose agent 8 and agent 10 are neighbours with agent 8 on the left of agent 10. Upon activation they communicate their numbers to each other. Agent 8 correctly communicates 8 as its number, but agent 10 makes an error and communicates 5 as its number. The two agents swap positions. Agent 8 is now on the right of agent 10. The system’s coordination decreases due to agent 8’s communication error. However, the communication error of agent 8 has no impact on the information communicated and decisions made by other pairs of agents. The decentralized system has a greater mean than the centralized system because the structure of communication in decentralized system dampens the impact of communication errors.
The centralized system has a greater variance of coordination than the decentralized system because the performance of the centralized system is more dependent on the specifics of who does what. In the centralized system, an individual agent’s communication error can trigger a cascade of misplacements of other agents. The size of a cascade due to an agent’s communication error depends on the exact error, the messages communicated by other agents, and the position of the agent who makes the communication error. These factors vary across simulations and so does the performance of the centralized system. In contrast to the centralized system, in the decentralized system the randomness generated by the error-prone behaviour of agents is dampened by the structure of interactions; decentralized interactions dilute the specifics of who does what.
Result 2 shows that the decentralized system takes more time than the centralized system to produce coordination. Figure 5 shows the number of time steps necessary for the decentralized system to exceed the mean coordination of the centralized system. The decentralized system takes more time than the centralized system to create coordination among agents. Furthermore, the number of time steps necessary for the decentralized system to exceed the mean coordination of the centralized system increases with the number of agents in the system. This is not because more interactions are necessary to order agents as the number of agents increases (there are as many interactions per time step as number of agents in the system). The structure of interactions in the decentralized system is such that the number of interactions per agent necessary for the decentralized system to outperform the centralized system increases with the number of agents.
4. Implications and empirical predictions
One may view real world economic structures like markets, firms, and governments as complex mixes of centralized and decentralized systems. Real world structures have a variety of other attributes, for instance markets have prices, firms have bureaus, and governments have parliaments. Despite their simplicity, the structures studied in this paper generate several implications and empirical predications about the world outside the window.
First, as communication technology improves, ceteris paribus, the organization of economic activities will become more centralized. Better communication technology allows for more accurate communication of information. This is equivalent to a decrease in communication errors in our model and consequent improvement in the relative performance of the centralized system. Perhaps this explains the emergence of behemoths like Walmart (Bowersox & Daugherty, 1995). Never before has a single firm employed nearly one percent of the US labour force (Axtell, 2001).
Second, autocratic societies will have greater variability than democratic societies. Empirical evidence suggests that dictatorships and other autocratic societies exhibit greater variability than democratic societies (Almeida & Ferreira, 2002; Doucouliagos & Ulubasoglu, 2008). Rodrik (1999) explains the greater variability of autocratic societies, and consequent collapse of economic growth, with their weaker ability to cope with external shocks. He argues that democratic societies have better internal conflict management mechanisms and therefore do not amplify external shocks as much as autocratic societies. Our paper provides an alternate explanation. We believe autocratic societies are less robust to communication errors of constituent parts than democratic societies because autocratic societies use more centralized decision-making than democratic societies. The greater variability and consequent extreme events in autocratic societies emerge from the way autocratic societies use dispersed information. In contrast to Rodrik’s model, our model predicts that autocratic societies will exhibit greater variance than democratic societies even in the absence of external shocks.
Third, economic organization will vary with product type. Certain personal services like massages involve information that is difficult to convey to higher levels of management. Information about standardized products like toothbrushes can be conveyed more accurately. It is more difficult to tell one’s manager what kind of massage a customer wants than to tell her what kind of toothbrush a customer wants. This is perhaps why one does not find massage parlours with thousands of employees. Stein (2002) presents evidence on how smaller banks provide relationship based small-business lending and larger banks provide services that involve easy to communicate information. Areas of economic activity where information is difficult to convey will be organized in a decentralized manner.
Fourth, urgent matters will be coordinated through centralized systems. This may be why most cities have a single fire-department but many housing agencies. Time is more significant in firefighting than in matching houses with buyers. The superior speed of the centralized system also explains the tendency to substitute decentralized systems with centralized systems in periods of war (Milward, 1979, p. 99–100). As Sun Tzu said what is of the greatest importance in war is extraordinary speed (Tzu, 2009).
5. Concluding remarks
In this paper, we studied alternate structures of communication and decision-making. The structure of relations between agents affects the performance of economic systems even when the structure does not influence incentives to communicate private information. Our insights shed light on the internal structure of corporations and the relations between government agencies. Our model answers some basic questions like why most cities have a single firm department but many housing agencies.
We have omitted a variety of factors relevant to the performance of economic systems including the computational limitations of information processing agents. But perhaps the greatest of omissions is an analysis of the relation between decentralization and the price system. Most economists believe markets are more decentralized than firms and governments (Axtell, 2003). Markets involve the use of the price system. Why does the most common form of decentralized coordination nearly always use the price system? Our hypothesis is that the price system decreases the time necessary to create coordination but makes markets less robust to communication errors. The price system is akin to a global telecommunication system which allows agents in one part of the system to know something about the plans of agents in other parts (Hayek, 1945). The price system decreases the time necessary for a decentralized system to produce coordination because prices tell agents more than what they learn from local interactions. With the price system fewer local interactions are necessary for coordination than without the price system. However, the price system also increases the dependence between the information communicated by different agents.
The impact of communication errors are no longer limited to their local vicinity. With the price system, communication errors influence the plans of agents far away from the interactions in which the errors occur. An increase in the dependence of the information communicated by different agents decreases the robustness of markets to communication errors. The influence of the price system on the robustness of markets is intricately linked to the business cycle phenomena. Exploring the relation between decentralization, the price system, and their consequence on aggregate fluctuations is a fruitful area for future research.
References
-
1
Technology, Information, and the Decentralization of the FirmThe Quarterly Journal of Economics 122:1759–1799.
-
2
Democracy and the variability of economic performanceEconomics & Politics 14:225–257.
-
3
When does coordination require centralization?The American Economic Review 98:145–179.
- 4
-
5
In Meeting the Challenge of Social Problems via Agent-Based Simulation (3–23)Economics as distributed computation, In Meeting the Challenge of Social Problems via Agent-Based Simulation (3–23), Tokyo, Springer.
- 6
- 7
-
8
Logistics paradigms: the impact of information technologyJournal of Business Logistics 16:65.
-
9
Democracy and economic growth: a meta-analysisAmerican Journal of Political Science 52:61–83.
-
10
Tradition and Public Administration77–87, How bureaucratic structure matters: An organizational perspective, Tradition and Public Administration, Basingstoke, Palgrave-MacMillan.
-
11
No Man Is an Island: The Impact of Heterogeneity and Local Interactions on Macroeconomic Dynamics. Laboratory of Economics and Management Working Paper1–29, No Man Is an Island: The Impact of Heterogeneity and Local Interactions on Macroeconomic Dynamics. Laboratory of Economics and Management Working Paper.
-
12
Varieties of Capitalism: The institutional foundations of comparative advantageNew York: Oxford University Press.
- 13
-
14
Redundancy, rationality, and the problem of duplication and overlapPublic Administration Review 29:346–358.
-
15
On the economic theory of socialism: part oneThe Review of Economic Studies 4:53–71.
-
16
Unraveling the central state, but how? Types of multi-level governanceAmerican Political Science Review 97:233–243.
-
17
Explicitly articulated strategy and firm performance under alternative levels of centralizationJournal of Management 28:611–627.
-
18
Incentives, information, and organizational formThe Review of Economic Studies 67:359–378.
-
19
Organised detachment: Clearinghouse mechanisms in financial marketsInformation and Organization 15:229246.
- 20
- 21
-
22
The organization of government in metropolitan areas: a theoretical inquiryAmerican Political Science Review 55:831–842.
-
23
Managing Horizontal Government: The Politics of Co-OrdinationPublic Administration 76:295–311.
-
24
Where did all the growth go? External shocks, social conflict, and growth collapsesJournal of Economic Growth 4:385–412.
-
25
The architecture of economic systems: Hierarchies and polyarchiesAmerican Economic Review 76:716–727.
-
26
The architecture of complexityProceedings of the American Philosophical Society 106:467–482.
- 27
-
28
Information production and capital allocation: decentralized versus hierarchical firmsThe Journal of Finance 57:1891–1921.
- 29
-
30
Cerebral Mechanisms in Behavior (1-41)The general and logical theory of automata, Cerebral Mechanisms in Behavior (1-41), New York, Wiley.
Article and author information
Author details
Publication history
- Version of Record published: August 31, 2017 (version 1)
Copyright
© 2017, Veetil
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

