1. Dynamic microsimulation
Download icon

Challenges and Opportunities of Dynamic Microsimulation Modelling

  1. Ann Harding
  1. NATSEM, University of Canberra, Australia. This article was originally presented as a plenary paper to the 1st General Conference of the International Microsimulation Association, Vienna, 21 August 2007.
Research article
Volume 16(2) Summer 2023
Cite this article as: A. Harding; 2023; Challenges and Opportunities of Dynamic Microsimulation Modelling; International Journal of Microsimulation; 16(2); 1-13. doi: 10.34196/ijm.00280

Abstract

Many of the social policy challenges facing the modern welfare state are long-term in nature, particularly the threats to future fiscal sustainability caused by population ageing. In such an environment, dynamic population microsimulation models provide one of the most useful available modelling tools for projecting the likely future distributional consequences of possible policy changes. However, the construction of such dynamic models remains an extremely difficult and costly undertaking, and this paper reviews some of the challenges posed by the construction of dynamic microsimulation models.

1. Introduction

Across much of the industrialised world, microsimulation models have become indispensable tools to policy makers. The modern welfare state today typically consists of a plethora of overlapping tax and outlay programs designed to meet multiple social policy objectives - including income redistribution and ensuring that most citizens enjoy an adequate standard of living and have reasonable access to such social services as health and education. These objectives are met through a very wide range of policy instruments, including both means-tested and universal cash transfers or service provision; means-tested and/or categorical eligibility for various tax concessions; and publicly-mandated insurance schemes or payments to be made by employers, employees or individuals. In an environment of such complexity, it is not surprising that policy makers attempt to reduce some of the risk associated with unintended or unexpected outcomes from policy change by using microsimulation models.

Microsimulation is a technique used to model complex real life events by simulating the actions of and/or impact of policy change on the individual units (micro units) that make up the system where the events occur. Microsimulation is a valuable policy tool used by decision makers to analyse the detailed distributional and aggregate effects of both existing and proposed social and economic policies at a micro level.

Static arithmetic microsimulation models that simulate the immediate or ‘morning after’ distributional impact upon households of possible changes in tax and transfer policy are today the most widely used type of microsimulation models. In many countries, policy makers have become accustomed to receiving highly disaggregated information about the likely distributional impact of possible policy reforms that they are considering.1 These impacts at the micro level are also summed to show the impact of the possible policy change upon aggregate tax revenues or upon government outlays. In Australia, for example, where static microsimulation models have been used within policy formulation for the last 15 to 20 years, there have been a number of cases where the shape of announced policy reforms was strongly affected by the results of microsimulation modelling.2

Traditionally, these static models have usually been ‘arithmetical’ calculators, where the models ‘simulate the change in the real disposable income of individuals or households due to a change in the rules for calculating tax or benefit payments under the assumption that individual behaviour is unchanged’ (Bourguignon and Spadaro, 2006). However, if the changes in government policy are sufficiently great, then they can be expected to have effects on labour supply (and thus on wages and aggregate employment) and/or on the prices facing consumers (and thus on demand for particular types of goods and services and subsequently on industry). In the past decade or so, greater efforts have been made to take into account these general equilibrium effects, by trying to link sectoral models to a household micro-database. As Bourguignon and Spardaro note, to date such efforts have limited ‘themselves to a subset of markets, most often the labour market’ (2006, p. 5) — with the Melbourne Institute, for example, having constructed the MITTS static microsimulation model, which simulates behavioural labour supply responses to policy change (Buddelmeyer et al., 2006).

Despite their undoubted other advantages, static microsimulation models usually illustrate the impact of policy change only for today’s world, perhaps at most looking four or five years into the future through the application of standard static ageing techniques (Harding, 1996). (The behavioural variants of these models typically abstract from the likely time path of changes in behaviour that in the real world could take years to unfold.)

However, in recent years many of the key policy challenges faced by the welfare state have required a much longer term perspective than that typically embodied in static microsimulation models (Cotis, 2003). In particular, the phenomenon of structural population ageing, where in decades to come a relatively smaller proportion of taxpayers will have to support a relatively larger proportion of retirees, has created a desire among policy makers to look at policy consequences five or more decades into the future. In essence, in many countries there are grave doubts about the extent to which generous cash transfer programmes for retirees or highly subsidised health and aged care services will continue to be affordable (see Harding and Gupta, 2007b).

In this environment, dynamic population microsimulation models have slowly become more popular, particularly during the past decade. Dynamic microsimulation models were the brainchild of Guy Orcutt who, frustrated by the macroeconomic models of the day, proposed a new type of model consisting of interacting, decision-making entities such as individuals, families and firms (1957). Dynamic models try to move individuals forward through time, by ‘updating each attribute for each micro-unit for each time interval’ (Caldwell, 1990, p. 5). Thus, the individuals within the original microdata or base file are progressively moved forward through time by making major life events - such as death, marriage, divorce, fertility, education, labour force participation etc. - happen to each individual, in accord with the probabilities of such events happening to real people within a particular country. Thus, within a dynamic microsimulation model, the characteristics of each individual are recalculated for each time period.

Dynamic cohort microsimulation models, which usually age only one or a series of cohorts, rather than an entire population, 3 appear to have been less attractive to policymakers than dynamic population microsimulation models, which attempt to simulate the futures of a large representative sample of the entire population of a nation. Thus, the most recent examples of ‘successful’ dynamic microsimulation models, which are feeding directly into social policy processes, largely appear to be dynamic population models, typically beginning with a comprehensive cross-section snapshot of the population at a particular point in time (such as a census) or, in some cases, with longitudinal administrative data.

After the formulation of the original idea by Orcutt (1957), he and a team of three graduate students built the first realisation of the model (Orcutt et al. 1961) and then in the 1970s the second realisation, the DYNASIM model, was constructed at the Urban Institute. However, in the 1980s, dynamic microsimulation languished (Caldwell, 1996). In the 1990s, while static microsimulation flourished due to the great improvements in microdata availability and quality, the quantum advances in computer software and hardware and the growing complexity of government programs (Harding and Gupta, 2007a), dynamic microsimulation grew more slowly. Caldwell recently pointed to some of the reasons why dynamic microsimulation effectively failed during the 1980s and early 1990s, including that the perceived benefits did not sufficiently outweigh the very substantial costs associated with constructing a dynamic population microsimulation model (Caldwell, 2006).

However, principally during the past 10 years, a number of important new dynamic population microsimulation models have been constructed, primarily because of the growing concern about population ageing. These include DYNASIM3, MINT and CBOLT within the US, DYNACAN within Canada, MOSART within Norway, SESIM within Sweden, and SAGE and PENSIM within the UK.4 These models are being actively used by policy makers to answer questions that cannot be as readily answered using any other modelling technique. For example, all of the above models have been used to shed light on whether future old age public pensions are affordable and on the distributional consequences of possible changes to the rules of those pension systems (Flood, 2007; Fredriksen et al., 2007; Favreault and Sammartino, 2002; Morrison, 2007; Butrica and Iams, 2000).

Other cell-based modelling approaches have also been used to examine the extent of future fiscal gaps due to population ageing. For example, the Australian Treasury has very successfully used cell-based models (dividing the population into a series of age/gender and other cells) to project likely future tax revenues and outlays, recently estimating that in 2046-47 Commonwealth outlays appear likely to exceed Commonwealth revenues by 3.5 per cent of GDP (Costello, 2007). Such projections have played an important role in public debate and public policy in Australia, helping to stimulate a series of policy reforms designed to increase labour force participation (including a series of welfare to work reforms and superannuation tax reforms). However, cell-based models cannot readily be used to examine the detailed distributional implications of alternative possible policy reforms (Harding, 1999). Answering these types of questions requires dynamic microsimulation models - which suggests that, despite the many challenges involved with constructing such models, millions of dollars will continue to be devoted to funding their development in the coming decades.

The following sections outline what the author sees as some of the major challenges associated with the construction of dynamic microsimulation models, with many of the issues posed being based on the experience of building the Australian Population and Policy Simulation Model (APPSIM), which NATSEM is currently constructing with 13 government agencies as research partners and with additional funding from the Australian Research Council. Construction of APPSIM commenced in late 2005 and the model is due for completion by mid 2010.

2. Challenges of dynamic microsimulation

2.1 Budgets and project management

The construction of a dynamic population microsimulation model, of a quality suitable to be used to underlie important government policy decisions, is a multimillion dollar exercise. It is probably important for modellers to be open about just how expensive such models are to build, so that they can help ensure that other academics or government departments do not embrace such projects with unrealistic expectations. For example, the developers of the MINT, CBOLT and POLISIM dynamic population microsmulation models within the US were recently kind enough to share with the author that the total development costs of each of these models to date has exceeded US$6 million. To an external observer looking at theteams of researchers involved for at least the past 10 years in the construction of the DYNACAN, MOSART and SESIM models, budgets of this magnitude are also clearly involved.

All of the models mentioned above were developed within government (although often with considerable input from academics). Within academia itself, researchers struggle to build dynamic population models on the shoestring budgets that are typically available from grant agencies. For example, the UK SAGE project received five years of grant funding of £0.8 million and, while other research activities were also included within this funding umbrella, the construction of the SAGE dynamic population microsimulation model was a key activity at the heart of the proposal. Given changes in personnel and the complexity of the processes being modelled, the model development took longer than anticipated and, although the model was finished during the funding cycle, this involved both an extension of time and the Chief Investigators having to donate significant amounts of their own time.

Similarly, the total current cash budget for the construction of APPSIM over the five years is under Aust$1.7m. Now that we are two years into this project, it has become clearer that this is an exceptionally modest budget for a project with a scope as ambitious as APPSIM’s. (For example, because of the importance of immigration to Australia the APPSIM model has to include a sophisticated migration module – which is an area many other dynamic models are able to ignore. Similarly, the APPSIM model is expected to include a module focused on the usage of health services and aged care which, again, is an area that many dynamic models, such as DYNASIM3, have not attempted to simulate.) This necessarily means that the project leaders are pursuing other strategies to help increase the total resources that can be allocated to the project, such as by attracting Visiting Fellows5 or additional PhD students.6

But this does not simply mean that academics and public servants need to be aware that they need to find considerable funds before attempting construction of a dynamic population MSM. The other, perhaps unanticipated, consequence of lengthy and expensive modelling infrastructure projects like the construction of a dynamic population MSM is the necessity for strong project management skills.

As Harding recently wrote: ‘With the benefit now of 15 years of experience in the construction of extremely large and complex microsimulation models, the crucial importance of project management has become clearer to me. Academics naturally tend to want to do an outstanding job in their modelling work — and this often means that the earlier stages of a project absorb a greater than anticipated share of the total time and budget for the project. The end result is that important processes that were part of the original project scope often then do not get included within the model — or they get included in a much more rudimentary way, or they are less well documented or validated or, by the time the model is completed, there are no more funds left to produce the papers that illustrate the useful questions that the model can answer (and thus to keep stakeholders and future funders engaged).’

‘Today, I would place a much greater importance on developing the simplest possible (but functioning) version of a model, on getting that well documented and on producing papers containing illustrative results within the project budget and timeframe. It is then easier to persuade stakeholders to provide additional funds to support refinements to particular modules or the development of new modules to simulate additional processes. Such an approach militates against the taking of risk, which was a feature of the development of [NATSEM’s] original DYNAMOD model (such as the use of survival functions and the attempt to build an intergrated macro model). But it seems to me to better reflect the reality of research funding today, given the very high costs associated with the construction of dynamic microsimulation models. One possible solution to this ‘risk’ dilemma is for PhD students to undertake the high-risk development of new methods and innovations, which can subsequently be included within the core model.’ (quoted in Cassells et al., 2006).

The SAGE team offered some similar observations when they very helpfully summarised some of the important lessons that they had learned in a presentation in December 2003 (Scott et al., 2003), by which time the project was nearing the end of its five year course. The first lesson was ‘keep it simple but credible’, with the authors noting that: ‘simplicity is necessary in order to obtain a model that starts functioning within the lifetime of an initial programme of work’ (2003, p. 19).

The second lesson was ‘keep it simple but flexible’. Thus, Scott et al write that ‘the primary goal of modelling work should be the construction of a model that provides at least initial answers to analytical questions of interest. However, the model should have the capacity to provide 'more complex' answers as additional modules are developed and refined’ (2003, p. 19). This suggests a phased program of research, where an initial working version of a dynamic model is constructed and then efforts are later made to improve or elaborate upon certain processes within the model.

Falkingham and Evandrou, two of the chief investigators on the SAGE project, added the following observations to guide future model builders, indicating that : ‘overall project management was critical to the task of building a fully functioning dynamic model within the timeframes and funding levels typically achieved via academic grants. Academics often underestimate the resources required to build a dynamic microsimulation model, both in terms of time and money. The funds required are typically at the upper limit of the research grants available from funding agencies and there is a temptation to reduce the resources requested to fit within funding limits. It is important to be realistic in what can be achieved within the project funds and time.’ (quoted in Cassells et al., 2006, p. 26).

So, in essence, the message for future dynamic MSM builders is to determine what modules are required in your model, divide the available time and funds between those modules based on your current best estimate of their relative importance and complexity, capture that information in a detailed work plan spanning the multiple years of the project, and then stick as ruthlessly as you can to that plan. Within every module, it will always be possible for you to do a better job if you devoted extra time and resources to it – but the temptation has to be resisted, because the consequence is likely to be a model that is not delivered and usable within the project time frame!

2.3 Collaboration and co-operation

When NATSEM began the construction of the Australian DYNAMOD dynamic population MSM, more than ten years ago now, there simply was not the accumulated body of knowledge about dynamic MSM that there is today. But now, very helpfully, an additional decade of experience in the construction and use of dynamic population MSM has been captured in a range of publications, including five published international collections derived from a series of international gatherings, including the regular Nordic microsimulation seminars, the Cambridge conference in 1998, the Maine conference in 2000, and the Canberra conference in 2003.7 This means that new model builders have an improved literature to draw upon about what works and what doesn’t, with extended debates having occurred during the past decade about such issues as how to best reduce stochastic error, how to improve ‘marriage market’ modelling, and how to most appropriately match summed micro results to external aggregate benchmarks (Neufeld, 2000; O’Donoghue, 2001; Kelly and King, 2001; Perese, 2002).

There is evidence that extended collaboration that includes access to the source code of an existing model (as well as on-going assistance from that earlier model’s developers) can help fast track model construction. For example, Morrison has stressed the importance of building DYNACAN on an existing platform (the CORSIM model), along with the co-operation and collaboration with CORSIM’s developer, Stephen Caldwell, as being two of the key ingredients for the success of DYNACAN (cited in Cassells et al., 2006). The CORSIM methodology has not only been utilised by Canada, but also by Sweden through the SVERIGE model and by POLISIM within the US Social Security Administration (McKay, 2003). Within Australia, although this is a static rather than a dynamic MSM example, it appears that the Australian Treasury has been helped in its construction of a behavioural (labour supply) static microsimulation model through access to the computer code of the Melbourne Institute’s MITTS model, as well as on-going consultation with its developers (King, 2007).

Another area of collaboration that appears to foster improved model development is that between academics and government. Falkingham and Evandrou, for example, have commented that ‘close liason with government departments and other users is important and can facilitate access to data and knowledge transfer (cited in Cassells et al., 2006, p. 26). Similarly, in the US, Favreault and Smith have noted the mutual benefits for both models created by the close co-operation that existed between theDYNASIM3 team located at the Urban Institute and the developers of the Social Security Administration’s MINT model (with the Urban Institute acting as contractors to help develop MINT) (2004, p. 1). Sweden offers another excellent example, where the development of SESIM within the Swedish Ministry of Finance was enhanced by collaboration with such eminent Swedish academics as Anders Klevmarken and Lennart Flood. Within Australia, the long-term contract for development and maintenance of the STINMOD static microsimulation model by NATSEM for the Commonwealth provides another example of successful long-term collaboration (Klevmarken, 2005).

One lesson to be drawn from both the Australian and international experience of the past 15 years is the importance of collaboration with and funding from government, if complex microsimulation models are to survive in the long-term. As Harding observes, ‘Construction and maintenance of such models outside government offers significant advantages, including that separation from the pressures of day-to-day policy development makes it easier to complete what can often be seen as less critical tasks within the policy hot-house (such as documentation). In addition, it creates the possibility of the model feeding into the policy deliberations of players outside government, with consequent benefits for the development of sound public policy within a country. But the costs of maintenance of complex microsimulation models are so high that it is difficult to keep them alive in the long-term without the injection of substantial public funds. This underlines the importance of academics understanding the requirements of their government clients and meeting those needs – and, conversely, government understanding the needs of academics, such as the need to publish’ (quoted in Cassells et al., 2006, p. 30). Morrison has similarly noted that that another of the factors underlying DYNACAN’s success has been the emphasis upon presenting results to clients and understanding their needs (quoted in Cassells et al., 2006, p. 17).

While international collaboration between model developers in different countries is clearly occurring, it is possible that much more could be done to facilitate this, subsequently offering the prospect of reducing model development costs. For example, the email forums provided by the International Microsimulation Association (IMA) provide one means to quiz fellow members about particular technical issues. But perhaps we could do more by, for example, enhancing the IMA website so that related papers are co-located – so that, for example, any model developer who had written a paper about alignment of dynamic microsimulation models or development of the earnings module within a dynamic MSM could load their paper into the ‘alignment’ or ‘earnings’ sub-section of the dynamic MSM areas of the IMA website. This would dramatically reduce the search time associated with locating all of the current papers dealing with a particular aspect of dynamic MSM development.

Similarly, since there is so much to be gained from not re-inventing the wheel in dynamic MSM, perhaps we could more actively encourage short fellowships or visits at the various active centres around the world.

2.3 Microdata quality

The builders of dynamic population MSMs face numerous and daunting data challenges. Two key data issues stand out: first, the choice of the base dataset for the model and the associated challenges that choice generates and, second, the quality of the longitudinal microdata used to estimate the various transition probabilities that move the simulated individuals from one state to another as they progress through time.

Typically, no base microdatset contains all of the information required by a dynamic population MSM (Scott et al., 2003). The dilemmas and choices facing the modeller are well summarised in Zaidi and Rake (2001) and Cassells et al. (2006), and typically comprise either a large Census sample (onto which various ‘history’ and other characteristics will have to be imputed) or longitudinal administrative data (which generally contain excellent information in certain restricted areas but require the imputation of additional characteristics onto the base dataset). Some models, such as DYNASIM, have matched administrative data to survey data to achieve a broad but detailed base population while others, such as SAGE, have matched survey data onto their base Census sample data to achieve the additional required information (Evandrou, 2004). While the exact techniques and data sources used to generate microdata of sufficient richness to serve as the base data for a dynamic population microsimulation model vary, in all cases the enhancement of the original base microdata involves considerable effort and resources. Where longitudinal earnings histories are not available, modellers have faced enormous challenges in attempting to ‘back-cast’ to simulate earnings (and other characteristics) earlier in life.

The second key data challenge facing most dynamic modellers is the quality and sample size of the longitudinal microdata available to estimate the transition parameters to be used within the dynamic model. Modellers in the English speaking countries typically have access to relatively small sample surveys, whose scope may span only a limited number of years. To take Australia as an example, most of the transition probabilities to be used within APPSIM will be estimated from the HILDA longitudinal dataset. HILDA samples around 7,000 households and, to date, five waves are available, starting in 2001-02.8

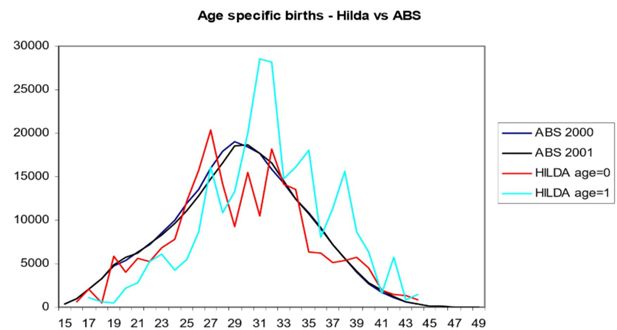
While HILDA represents a vast improvement in the availability of longitudinal data within Australia, its relatively small sample size means that there will be sampling error contained within the estimates produced from it. Figure 1, taken from Bacon and Pennec (2007a), charts the number of children aged 0 and 1 from HILDA against ABS data on births in 2000 and 2001. The difference between the two raises obvious questions about the extent to which the HILDA data can be used with confidence to estimate fertility within APPSIM. It also raises questions about the number of explanatory variables that can be used with confidence within the predictive equations. For example, while one might posit a theoretical model that suggests that the likelihood of having a child depends upon mother’s age, education, marital state, duration within current marital state, duration since last birth, current labour force status etc etc, there will be practical limits to the extent to which such predictive factors can be estimated from small longitudinal samples.

Figure 1
Download asset Open asset
Comparison of births in HILDA sample survey data and ABS estimates

Another key problem raised by Bacon and Pennec is that the relatively slender five year time frame currently captured within the HILDA data may result in the production of biased estimates, because five years is not sufficient to capture critical dynamics which have been occurring in the longer term. For example, longer-term macrodemographic data suggest that the age at first marriage for females has been rising systematically in Australia during the past decade (Bacon and Pennec, 2007). It could thus be argued that uncritically simulating first marriage probabilities in APPSIM using transition equations derived from the HILDA survey would result in too many young brides in 2020.

A final issue is that even if comprehensive longitudinal microdata spanning some decades are available, the resulting transition equations might still not give the ‘right’ answers about the future, because human behaviour can change remarkably quickly. The changes in divorce rates following major legislative change in both Canada and Australia provide one extreme example, while the rapid fall in fertility in Australia in the 1970s provides another.

Overall, it is clear that the data challenges facing the dynamic microsimulation modeller are very considerable!

2.4 Alignment

The above discussion leads naturally to the issue of alignment. Given that the microdata used to estimate the transition equations within dynamic MSM are often subject to sampling error; or do not contain critical characteristics for explaining behaviour; or capture too short a period of time to reflect longer-term evolution in behaviour; or capture behaviour that is about to change for reasons not self-evident at the time the modelling was undertaken, it is hardly surprising that the predictions of unaligned dynamic microsimulation models can drift away from such benchmark aggregates as official population projections.

The ability to align the micro output to benchmark macro estimates has emerged as a crucial component of many models in the past few years. Alignment is one area where there has been substantial methodological work undertaken in the past decade, resulting in the development of an international consensus about the need for alignment. Today, ‘almost all existing dynamic microsimulation models are adjusted to align to external projections of aggregate or group variables when used for policy analysis’ (Anderson, 2001, p. 2-6).

Aligning the micro values produced by dynamic models with known or projected macro aggregates usually involves some modification of model estimates. Whilst this modification does change aggregate outputs of the model, it generally doesn’t change the distributions, preserving the microeconomic content (Anderson, 2001, p. 2-6).

There are a range of reasons why the summed results of dynamic population microsimulation models might need to be forced to match external aggregate data, apart from the possible concerns about the quality of the equation estimations outlined above. One is that many countries have official population projections, so that model results that drift away from these ‘official’ numbers might not be taken seriously by policy makers. Another is that the summed results of some of the dynamic models have to match the official actuarial projections of their agencies – that is, there has to be a consistency between the macro actuarial projections and the summed micro results.

It is important to be clear here that macro does not mean simply ‘macro-economic’, but also any other important macro or aggregate outcomes, such as macrodemographic outcomes. For example, DYNACAN aligns to target rates for mortality, fertility, migration, marriage and divorce propensities and SESIM is constructed to easily align to different exogenous demographic and macroeconomic assumptions. The earlier attempt within DYNAMOD to build a linked economic macro-micro model failed and dynamic population MSMs have subsequently usually adopted simpler strategies, such as forcing summed unemployment rates from the microdata to align with an exogenously specified aggregate unemployment rate. However, there is increasing interest internationally in building much more sophisticated macroeconomic to microeconomic linkages (Fredriksen et al., 2007; Bourguignon and Spadaro, 2006).

Within Europe, recent research in demography, termed MICMAC, has argued for the development of population forecasting models that explicitly link microsimulation models to macrosimulation models. As explain, MicMac offers a bridge between aggregate projections of cohorts (Mac) and projections of the life course of individual cohort members (Van der et al., 2005, p. 1). One could argue in favour of a highly disaggregated macrosimulation model to run in tandem with the microsimulation model component – with the macrosimulation model potentially disaggregated, for example, by age group, gender, and marital status. One could then imagine a model where a policymaker could affect fertility in 2025 by adjusting the microeconomic equations or, alternatively, by adjusting the macrosimulation targets for specified groups.

While some degree of macro-micro linkage now appears to be seen as inevitable within dynamic models, there are also considerable uncertainties about the issues involved. One is that the effort and cost involved in constructing a macrodatabase for all modules may turn out to be too high, given the limited budget and time frame for the development of models. Another is that it is not yet clear whether multiple alignment processes will slow the run times for a model (O’Donoghue, 2001, p. 15). A third is that if everything is aligned at a very disaggregated level (e.g. predicted first marriage rates by age, gender and education groups), will this act to reduce the predictive usefulness of the dynamic model, by imposing upon the micro results predetermined macro outcomes?

As an interim measure, APPSIM is being designed with a facility to turn the macro alignment facility ‘on’ or ‘off’ within each module. A decision about the desired extent of macro alignment will be made once it becomes clearer whether and where the micro results drift sharply away from accepted Australian benchmark aggregates.

2.5 User friendliness

One of the other lessons learnt within Australia from experience with the earlier DYNAMOD model is the importance of user-friendliness. A dynamic population MSM is clearly an extraordinarily complex beast – but this does not mean that every effort should not be made to make it easy to use. During the past few decades some key lessons have been learnt by dynamic modellers that should be emulated by new modellers.

One is the modularisation of model structure, so that it is easier to amend or delete parts of the model. One lesson from the DYNASIM experience, according to the excellent review of models by Zaidi and Rake, is that ’the subdivision of the model into smaller modules is important. This aspect of dynamic microsimulation … helps to make the working of the model more systematic and makes it easier to check problems at different stages in the running of the model’ (Zaidi and Scott, 2001, p. 8).

Another is parameterising modules and holding all key parameters separate from the actual operation of the modules, so as to allow changes to be made more easily (see for example Citro and Hanushek, 1991, p. 156; Zaidi and Rake, 2001, p. 18). Within APPSIM, for example, all parameters (including regression equation coefficients) are held within Excel spreadsheets that can be easily amended by the user and then are imported into C# (the main programming language for the model).

Similarly, as Morisson has described for DYNACAN (2006), every attempt should be made to make output easily available, with DYNACAN producing an extensive standard suite of possible output tables and charts (which can be augmented by more detailed analysis by the user).

The importance of encouraging user input has also been well noted by modellers, including within the EUROMOD project, which concluded that ‘[user] consultation can only result in a better model, more widely used’ (Sutherland, 1997, p. 17). EUROMOD has gone to great lengths to seek user input and consultation. For example, trial versions of the model at different stages of development were provided to potential users to ensure that users’ views were known and could be incorporated during the development of the model.

2.6 Behavioural response and the macro-economy

As Bourguignon and Spadaro helpfully note, until recently most dynamic microsimulation models have been ‘dynamic arithmetical’ models (2006, p. 32), in the sense that they have not allowed for changes within the model in the behaviour of individuals initiated by government tax-transfer policy change. In addition, they have often not allowed for possible macro-economic effects in response to government policy changes. Thus, traditionally, dynamic microsimulation models have often been ‘dynamic’ in the sense that the characteristics of individuals have been updated in each time period (e.g. a woman having a baby might be simulated to leave the labour force), rather than being dynamic in allowing feedback effects in behaviour from government policy change and macro-economic change. DYNASIM3, for example, retains the traditional structure of DYNASIM, where all of the demographic and annual labour market histories are simulated first and written out to file, and then the rules of various tax and social security programs are simulated separately (Favreault and Smith, 2004). The MINT model follows a similar structure. This means that changes in social security benefits, for example, cannot affect retirement behaviour.

Within Australia Keegan has recently argued that it would be desirable to be able to allow changes in tax-transfer policy to affect labour supply within the APPSIM model, given that many of the policies likely to be on the reform agenda will be designed to encourage delay in the retirement of the baby boomers or to encourage women to re-enter the labour force after periods of absence (Keegan, 2007). Bourguignon and Spadaro similarly argue in favour of continuing to pursue macro-micro linkages, both linking general equilibrium macro-economic models to microsimulation models and allowing behavioural responses (2006). As with static modelling, advances are now being made on both of these fronts (Aaberge et al., 2007; Fredriksen et al., 2007).

But there are some considerable uncertainties and challenges here for dynamic modellers. While it is believed that the developers of SESIM have developed some labour supply response effects within their model, the exact details of the methodology are not clear. O’Donoghue provides a particularly clear description of the behavioural vs probabilistic model dilemma, noting that ‘incorporating behavioural responses into microsimulation models has been found to be very difficult (2001, p. 13).

The path to bolting together a MITTS type model that optimises labour supply (with MITTS being a static microsimulation model) with a dynamic microsimulation model like APPSIM, is thus not a well-trodden one and may not turn out to be workable. In developing APPSIM, Keegan may experiment with other possible proxy methods for capturing some labour supply response effects, perhaps by making the probability of entering or remaining in the labour force dependent upon the earnings replacement rates indicated by the proposed new tax-transfer policies.

Experienced dynamic microsimulation modellers are also uncertain about what will happen if inter-acting behavioural links are created within their models – for example, if labour supply depends on health status and health status depends upon labour force status.

3. Conclusions

This review has made it clear that the construction of a reliable dynamic population microsimulation model for use in social policy formulation is a very demanding multi-year project. Indeed, the degree of effort involved seems more akin to the large scale multi-million dollar projects that occur in the natural sciences. In the social sciences, such large projects are relatively unusual — and many social scientists would not have extensive experience in managing projects of this scale and time span. In summary, construction of a dynamic population microsimulation model remains a demanding task!

While the practical constraints created in the past by computing hardware and software have now been very substantially reduced, the data demands of dynamic population MSMs remain problematic. Creating a base population data set of sufficient quality with the requisite range of historic and other variables continues to be a major challenge, as does estimating suitable transition equations from available longitudinal microdata.

A consensus appears to have emerged during the past decade about the need for alignment of the micro projections to future macro economic and demographic aggregates, but there is still debate about the level of disaggregation at which this should occur and about how extensive any such alignment should be.

Although not discussed earlier in this paper, there has also been an emerging consensus about the usefulness of discrete rather than continuous time models (with the key models being used in policy simulation today now adopting this time unit), and about the importance of adequate documentation of the models (see Cassells et al., 2006).

In addition, international and earlier Australian experience has pointed to the risks of models being ‘too complex, too soon’, suggesting that the goal of the first version of a dynamic population model should be to construct a functioning model that is as simple as possible, with the aim of creating valuable deliverables for clients that can be developed progressively and enhanced over time.

The international experience has also indicated that the institutional framework within which dynamic models are developed is important for determining their long-term survival. Sustained funding from government appears to be required to maintain dynamic models, given the sheer size and complexity of the task — while academic input helps to generate innovation and provide ideas about new directions and applications. Overall, this suggests that a long-term partnership between academia and government will be required for a dynamic population model to first become and then remain part of the established modelling infrastructure.

Despite the challenges posed by dynamic microsimulation, considerable efforts are likely to continue to be made to develop and improve such models, simply because the forthcoming fiscal challenges caused by population ageing should prompt investment in the requisite modelling infrastructure. In addition, the success in the past five years of dynamic microsimulation models such as SESIM, MOSART and DYNACAN - where the models are up and running and influencing policy - is a very encouraging development internationally.

Footnotes

1.

In Europe, for example, Sutherland has played a key role in the development of EUROMOD, which simulates the tax and transfer systems of each EU country (Sutherland, 2007; Immervoll et al., 2006); in the US the TRIM model continues to flourish (O’Hare, 2000, http://trim.urban.org); Statistics Canada continues to develop the publicly available SPSD/M model (Murphy, 2000); while, in Australia, NATSEM’s publicly available STINMOD model is used for a wide variety of policy analyses (Harding et al., 2006; Lloyd, 2007; Toohey and Beer, 2004).

2.

To give just two examples, the STINMOD microsimulation model was used to analyse the distributional impact of the sweeping package of tax reforms proposed by the government in the late 1990s, (Warren et al. 1999) and these results were one of the factors that prompted changes in the shape of the proposed package; and a variant of the STINMOD model was used to support the deliberations of the Ministerial Taskforce on Child Support, with these results feeding directly into their final proposals for change in the Australian Child Support Scheme (Ministerial Taskforce on Child Support, 2005).

3.

Such models have been used to analyse lifetime income distribution and redistribution, lifetime rates of return to education, repayment patterns for student income-contingent loans, and the impact of proposals for including homemakers in the Canada Pension Plan (Baldini, 2001; Falkingham and Harding, 1996; Falkingham and Hills, 1995; Hain and Helberger, 1986; Harding, 1993a; 1993b; 1995; O’Donoghue, 2002; Wolfson, 1988). A variant on the more usual theme is the LifePaths model constructed by Statistics Canada, which processes a series of cohorts through their lifetimes and in which the cohorts can be placed ‘side by side’ to produce a cross-sectional snapshot (Gribble et al., 2003).

4.

Chapters on SESIM, DYNACAN, SAGE, and MOSART are in Gupta and Harding 2007. For CBOLT see the page established by John Sabelhaus at http://www.bsos.umd.edu/econ/sabelhaus/cbolt_documents.htm. For MINT see Butrica and Iams, 2000.

5.

For example, Dr Sophie Pennec, from the French Institut National d’Etudes Démographiques (INED), recently spent more than 12 months at NATSEM as a Visiting Fellow, with funding support from INED and the FEAST grant scheme. Dr Pennec played a crucial role in the construction of the demographic and family formation modules within APPSIM.

6.

With Harding recently applying jointly with the Australian Department of Health and Ageing to the Australian Research Council for funds for a PhD scholarship, with development of the APPSIM health status and health service usage module being the proposed PhD topic.

7.

For the five edited collections, see Harding, 1996; Harding and Gupta, 2007b; Harding and Gupta, 2007a; Mitton et al., 2000; Gupta and Kapur, 2000. For the papers from the most recent Nordic microsimulation seminar see www.ssb.no/english/research_and_analysis/conferences/misi/.

8.

For the latest details on HILDA, see http://melbourneinstitute.com/hilda/

References

  1. 1
    Modelling Our Future: Population Ageing, Social Security and Taxation
    1. R Aaberge
    2. U Colombino
    3. E Holmøy
    4. B Strøm
    5. T Wennemo
    (2007)
    Population ageing and fiscal sustainability: integrating detailed labour supply models with CGE models, Modelling Our Future: Population Ageing, Social Security and Taxation, North-Holland, Amsterdam.
  2. 2
    Models for Retirement Policy Analysis
    1. JM Anderson
    (2001)
    USA: Report to the Society of Actuaries.
  3. 3
    APPSIM – Family Formation and Dissolution
    1. B Bacon
    2. S Pennec
    (2007)
    Working Paper No 6, National Centre for Social and Economic Modelling.
  4. 4
    Model Validation: Microsimulation and Macrosimulation, Presentation to APPSIM Technical Advisory Group, National Centre for Social and Economic Modelling
    1. B Bacon
    2. S Pennec
    (2007a)
    Canberra: University of Canberra.
  5. 5
    Inequality and Redistribution over the Life-Cycle in Italy: An Analysis with a Dynamic Cohort Microsimulation Model
    1. M Baldini
    (2001)
    Brazilian Electronic Journal of Economics 4:2.
  6. 6
    Microsimulation as a Tool for Evaluating Redistribution Policies
    1. F Bourguignon
    2. A Spadaro
    (2006)
    Working Paper 2006-20, Society for the Study of Economic Inequality.
  7. 7
    Evaluation of policy options to encourage welfare to work
    1. H Buddelmeyer
    2. J Freebairn
    3. G Kalb
    (2006)
    Paper presented at the 8th Nordic Seminar on Microsimulation Models.
  8. 8
    Divorced women at retirement: projections of economic well-being in the near future
    1. BA Butrica
    2. HM Iams
    (2000)
    Social Security Bulletin 63:3–12.
  9. 9
    Static, Dynamic and Mixed Microsimulation, mimeo, Department of Sociology
    1. S. Caldwell
    (1990)
    Ithaca, New York: Cornell University.
  10. 10
    Microsimulation and Public Policy
    1. S Caldwell
    (1996)
    505–522, Health, welfare, pensions and life paths: the CORSIM dynamic microsimulation model, Microsimulation and Public Policy, NorthHolland, Amsterdam, p.
  11. 11
    Paper Presented to the 8th Nordic Seminar on Microsimulation Models
    1. S Caldwell
    (2006)
    Dynamic microsimulation: directions for improvement, Paper Presented to the 8th Nordic Seminar on Microsimulation Models, Oslo, Norway.
  12. 12
    Problems and Prospects for Dynamic Microsimulation: A Review and lessons for APPSIM
    1. R Cassells
    2. A Harding
    3. S Kelly
    (2006)
    Discussion Paper no. 63, National Centre for Social and Economic Modelling.
  13. 13
    The Uses of Microsimulation Modelling, 1
    1. CF. Citro
    2. EA. Hanushek
    (1991)
    Washington: Review and Recommendations, National Academy Press.
  14. 14
    Intergenerational Report 2007
    1. P Costello
    (2007)
    Canberra: Commonwealth Treasury of Australia.
  15. 15
    OECD Observer
    1. J Cotis
    (2003)
    1, Population ageing: facing the challenge, OECD Observer, Vol, 239, p.
  16. 16
  17. 17
    Microsimulation and Public Policy
    1. J. Falkingham
    2. A. Harding
    (1996)
    233–265, Poverty alleviation vs social insurance systems: a comparison of lifetime redistribution, Microsimulation and Public Policy, North-Holland, Amsterdam.
  18. 18
    The Dynamic of Welfare: The Welfare State and the Life Cycle
    1. J. Falkingham
    2. J. Hills
    (1995)
    New York: Prentice-Hall.
  19. 19
    AARP Public Policy Institute
    1. M Favreault
    2. FJ Sammartino
    (2002)
    AARP Public Policy Institute, No, 2002–11,, Washington, DC, AARP.
  20. 20
    A Primer on the Dynamic Simulation of Income Model (DYNASIM3)
    1. M Favreault
    2. K Smith
    (2004)
    Washington: The Retirement Project, The Urban Institute.
  21. 21
    Modelling Our Future: Population Ageing, Social Security and Taxation
    1. L Flood
    (2007)
    Can we afford the future? an evaluation of the new Swedish pension system, Modelling Our Future: Population Ageing, Social Security and Taxation, Amsterdam, North-Holland.
  22. 22
    Modelling Our Future: Population Ageing, Social Security and Taxation
    1. D Fredriksen
    2. KM Heide
    3. E Holmøy
    4. IF Solli
    (2007)
    Macroeconomic effects of proposal pension reforms in Norway, Modelling Our Future: Population Ageing, Social Security and Taxation, Amsterdam, North-Holland.
  23. 23
    Modelling Our Future: Population, Ageing, Health and Aged Care
    1. D Fredriksen
    2. N Stølen
    (2007)
    MOSART, Modelling Our Future: Population, Ageing, Health and Aged Care, North-Holland, Amsterdam.
  24. 24
    The LifePaths microsimulation model
    1. S Gribble
    2. C Hicks
    3. G Rowe
    (2003)
    Paper presented at the International Microsimulation Conference on Population Ageing and Health: Modelling Our Future.
  25. 25
    Microsimulation in Government Policy and Forecasting
    1. A Gupta
    2. V Kapur
    (editors) (2000)
    Amsterdam: North Holland.
  26. 26
    Microanalytic Simulation Models to Support Social and Financial Policy
    1. W Hain
    2. C Helberger
    (1986)
    251–270, Longitudinal simulation of lifetime income, Microanalytic Simulation Models to Support Social and Financial Policy, Amsterdam, North-Holland, p.
  27. 27
    Lifetime Income Distribution and Redistribution: Applications of a Microsimulation Model
    1. A Harding
    (1993a)
    Amsterdam: North-Holland.
  28. 28
    Lifetime vs Annual Tax-Transfer Incidence: How Much Less Progressive?
    1. A Harding
    (1993b)
    Economic Record 69:179–192.
    https://doi.org/10.1111/j.1475-4932.1993.tb01812.x
  29. 29
  30. 30
    Microsimulation and Public Policy
    1. A Harding
    (1996)
    Amsterdam: North-Holland.
  31. 31
    Policy Implications of the Ageing of Australia’s Population
    1. A Harding
    (1999)
    Modelling Techniques for Examining the Impact of Population Ageing on Social Expenditure, Policy Implications of the Ageing of Australia’s Population, Melbourne, Productivity Commission.
  32. 32
    Modelling Our Future: Population Ageing, Social Security and Taxation
    1. A Harding
    2. A Gupta
    (2007)
    Introduction and overview, Modelling Our Future: Population Ageing, Social Security and Taxation, Amsterdam, North-Holland.
  33. 33
    Modelling Our Future: Population Ageing, Social Security and Taxation
    1. A Harding
    2. A Gupta
    (2007b)
    Amsterdam: North-Holland.
  34. 34
    AMP NATSEM Income and Wealth Report Issue 14, Sydney, September
    1. A Harding
    2. A Payne
    3. QN Vu
    4. P Percival
    (2006)
    AMP NATSEM Income and Wealth Report Issue 14, Sydney, September, www.amp.org.au/ampnatsemreports.
  35. 35
    The Distributional Effects of Government Spending and Taxation
    1. H Immervoll
    2. H Levy
    3. C Lietz
    4. D Mantovani
    5. C O’Donoghue
    6. H Sutherland
    7. G Verbist
    (2006)
    135–165, Household incomes and redistribution in the European Union: quantifying the equalizing properties of taxes and benefits, The Distributional Effects of Government Spending and Taxation, Basingstoke, Hampshire, Palgrave Macmillan, p.
  36. 36
  37. 37
    Australians over the coming 50 years: providing useful projections
    1. S Kelly
    2. A King
    (2001)
    Brazilian Electronic Journal of Economics 4:2.
  38. 38
    Participation Modelling in the Australian Treasury
    1. A King
    (2007)
    Paper for presentation at the 1st General Conference of the IMA.
  39. 39
    Dynamic microsimulation for policy analysis – problems and solutions
    1. NA Klevmarken
    (2005)
    2005 Australian Conference of Economists.
  40. 40
    Modelling Our Future: Population Ageing, Social Security and Taxation
    1. R Lloyd
    (2007)
    STINMOD: use of a static microsimulation model in the policy process in Australia, Modelling Our Future: Population Ageing, Social Security and Taxation, Amsterdam, North-Holland.
  41. 41
    Dynamic microsimulation at the U.S
    1. S McKay
    (2003)
    Social Security administration, Paper presented at the International Microsimulation Conference on Population Ageing and Health.
  42. 42
    In the Best Interests of Children – Reforming the Child Support Scheme
    1. Ministerial Taskforce on Child Support
    (2005)
    Canberra: Commonwealth of Australia.
  43. 43
    Microsimulation Modelling for Policy Analysis
    1. L Mitton
    2. H Sutherland
    3. M Weeks
    (editors) (2000)
    Cambridge: Cambridge University Press.
  44. 44
    Modelling Our Future: Population Ageing, Social Security and Taxation
    1. R Morrison
    (2007)
    Pension analysis using dynamic microsimulation: adding private pensions to the Canadian DYNACAN model, Modelling Our Future: Population Ageing, Social Security and Taxation, Amsterdam, North-Holland.
  45. 45
    Microsimulation in Government Policy and Forecasting
    1. B Murphy
    (2000)
    587–592, SPSD/M, Microsimulation in Government Policy and Forecasting, Amsterdam, North-Holland, p.
  46. 46
    Microsimulation in Government Policy and Forecasting
    1. C Neufeld
    (2000)
    361–382, Alignment and variance reduction in DYNACAN, Microsimulation in Government Policy and Forecasting, Amsterdam, North-Holland, p.
  47. 47
    Dynamic microsimulation: a methodological survey
    1. C O’Donoghue
    (2001)
    Brazilian Electronic Journal of Economics 4:2.
  48. 48
    Redistribution over the lifetime in the Irish tax-benefit system: an application of a prototype dynamic microsimulation model for Ireland
    1. C O’Donoghue
    (2002)
    Economic and Social Review 32:191–216.
  49. 49
    Microsimulation in Government Policy and Forecasting
    1. J O’Hare
    (2000)
    581–586, TRIM3, Microsimulation in Government Policy and Forecasting, Amsterdam, North-Holland, p.
  50. 50
    A New Type of Socio-Economic System
    1. GH Orcutt
    (1957)
    The Review of Economics and Statistics 39:116.
    https://doi.org/10.2307/1928528
  51. 51
    Microanalysis of Socioeconomic Systems: A Simulation Study
    1. G Orcutt
    2. M Greenberger
    3. J Korbel
    4. R Wertheimer
    (1961)
    New York: Harper and Row.
  52. 52
  53. 53
  54. 54
    The EUROMOD Preparatory Study: A Summary Report, DAE Working Papers Amalgamated Series no.9725, Department of Applied Economics
    1. H. Sutherland
    (1997)
    University of Cambridge.
  55. 55
    Modelling out Future: Population Ageing, Health and Aged Care
    1. H Sutherland
    (2007)
    EUROMOD – the tax-benefit microsimulation model for the European Union, Modelling out Future: Population Ageing, Health and Aged Care, Amsterdam, North-Holland.
  56. 56
    Financial incentives for working mothers under a new tax system
    1. M Toohey
    2. G Beer
    (2004)
    Australian Journal of Labour Economics 7:53–69.
  57. 57
    Combining micro and macro approaches in demographic forecasting
    1. GN Van der
    2. J de Beer
    3. J Beer
    4. F Willekens
    (2005)
    Paper prepared for Joint Eurostat-ECE Work Session on Demographic Projections.
  58. 58
    Main Report, Senate Select Committee on a New Tax System, Senate Printing Unit, April
    1. N. Warren
    2. A. Harding
    3. M. Robinson
    4. S. Lambert
    5. G. Beer
    (1999)
    445–508, Distributional Impact of Possible Tax Reform Packages, Main Report, Senate Select Committee on a New Tax System, Senate Printing Unit, April.
  59. 59
    Homemaker pensions and lifetime redistribution
    1. MC Wolfson
    (1988)
    Review of Income and Wealth 34:221–250.
    https://doi.org/10.1111/j.1475-4991.1988.tb00569.x
  60. 60
  61. 61

Article and author information

Author details

  1. Ann Harding

    NATSEM, University of Canberra, Canberra, Australia. This article was originally presented as a plenary paper to the 1st General Conference of the International Microsimulation Association, Vienna, 21 August 2007.

Funding

No specific funding for this article is reported.

Acknowledgements

The author would like to gratefully acknowledge the funding provided by the Australian Research Council (under grant LP0562493) for the development of APPSIM, and by the 13 research partners to the grant: Treasury; Communications, Information Technology and the Arts; Employment and Workplace Relations; Health and Ageing; Education, Science and Training; Finance and Administration; Families, Community Services and Indigenous Affairs; Industry, Tourism and Resources; Immigration and Multicultural Affairs; Prime Minister and Cabinet; the Productivity Commission; Centrelink; and the Australian Bureau of Statistics. The author would also like to acknowledge the two international partner investigators on this grant, Professors Jane Falkingham and Maria Evandrou of the University of Southampton.

Publication history

  1. Version of Record published: August 31, 2023 (version 1)

Copyright

© 2023, Harding

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Download citations (links to download the citations from this article in formats compatible with various reference manager tools)

Open citations (links to open the citations from this article in various online reference manager services)

Categories and tags