
Integrated computable general equilibrium (cge) micro-simulation approach
Abstract
Conventionally, the analysis of macro-economic shocks and the analysis of income distribution and poverty require very different methodological techniques and sources of data. Over the last decade however, the natural divide between both approaches has diminished, as evaluating the impact of macro-economic shocks on poverty and income distribution within a CGE framework complemented by household survey data has flourished. This paper focuses on explicitly integrating into a CGE model each household from a nationally representative household survey. The aim of this paper is threefold. First, we show that explicitly modelling each household in the CGE model addresses Kirman’s critique (1992) and overcomes the strong micro-economic assumption of representative agent. Second, we respond, albeit in a simple way, to the recommendation of Bourguignon and Perreira (2003) to integrate “real” households within a CGE framework rather than using representative households. Third, by providing applications to Nepal and the Philippines, we demonstrate that this technique is straightforward to implement and requires only a standard CGE model and a nationally representative household survey with information on household income and consumption.
1. Introduction
Conventionally, the analysis of macro-economic shocks and the analysis of income distribution and poverty require very different methodological techniques and sources of data. Owing to their economy-wide effects, macro-economic shocks are examined within the context of a computable general equilibrium (CGE) model based on consistent national accounts data but with the strong micro-economic assumption of one or a few representative households. On the other hand, income distribution and poverty issues are normally analysed within a partial equilibrium framework, based on household or individual level data to account for agents’ heterogeneity. Over the last decade however, the natural divide between both approaches has diminished, as evaluating the impact of macro-economic shocks on poverty and income distribution within a CGE framework complemented by household survey data has flourished.
Unlike the sequential approaches presented in the preceding papers, this paper focuses on explicitly integrating into a CGE model each household from a nationally representative household survey. The aim of this paper is threefold. First, we show that explicitly modelling each household in the CGE model addresses Kirman’s critique (1992) and overcomes the strong micro-economic assumption of representative agent. Second, it responds, albeit in a simple way, to the recommendation of Bourguignon and Perreira (2003) to integrate “real” households within a CGE framework rather than using representative households. Third, by providing applications to Nepal and the Philippines, we demonstrate that this technique is straightforward to implement and requires only a standard CGE model and a nationally representative household survey with information on household income and consumption.
The rest of the paper is organized as follows. Section 2 presents the conceptual problems raised by the representative household approach in general equilibrium models, and offers a fully integrated micro-simulation approach as an alternative. Section 3 describes the basic steps to follow to integrate and implement the integrated CGE microsimulation approach and offers some advice on data treatment through illustrations for Nepal and the Philippines. Section 4 discusses simulation results for both the Philippines and Nepal, while section five concludes on the usefulness of this approach.
2. Conceptual problems in the representative household approach
Although poverty and income distribution analysis within a CGE framework began in the late 1970s (Adelman & Robinson, 1978; Lysy & Taylor, 1980; Dervis et al., 1982), it is not until the late 1990s that this line of research became widespread. One reason is the proliferation of nationally representative household surveys with detailed income information over the course of the decade. Another is that, until recently, CGE modellers have generally shown little interest in the distributive impacts of policies—preferring to focus on welfare effects in terms of equivalent variation (EV) or compensating variation (CV). Nonetheless, the use of CGE models complemented with household survey data is now recognized as well-suited to identifying the mechanisms by which macro-economic shocks affect poverty and income distribution (Winters et al. 2004; Hertel & Reimer 2005).
The traditional approach, as summarized by Lofgren et al. (2004), makes use of “representative” households rather than actual/real households. Distributive impacts are simply captured through extending the disaggregation of the representative households in order to identify as many household categories, generally corresponding to different socio-economic groups, as possible. This approach makes it possible to analyze the impacts of policies on incomes and welfare between groups (inter-group distribution) but not within groups as intra-household distribution is assumed to be fixed. It provides information neither on poverty impacts (as the poor may be found in many different socio-economic groups and in varying proportions) nor on intra-group distribution. In order to address the first limitation, some authors have applied a fixed income distribution function among households within each household group in order to compute poverty indices (such as the FGT indices). One way is to assume a log-normal distribution, where the variance is estimated from the base year data (De Janvry et al., 1991). Meanwhile, Decaluwé et al. (2000) argue that a beta distribution is preferable to other distributions because it can be skewed to the left or right and thus may better represent the types of income distributions commonly observed within household groups. Yet, Boccanfuso et al. (2003) underscore the difficulty of using restrictive functional forms as distribution could change before and after simulations, and large variations in poverty indices may arise depending on the functional form employed.
The representative household approach is based on a very strong theoretical assumption that could be formulated as follows: the choices of households belonging to a given category may be represented by the choices of a unique household that maximizes its utility in such a way that these choices coincide with the aggregated choices of a large number of heterogeneous individuals. Kirman (1992) argues that this hypothesis is not very realistic given that, outside the most restrictive behavioural hypotheses: (1) there is no theoretical justification to affirm that the aggregation of individual choices necessarily leads to the same solution as the choice of a representative individual, (2) there is no guaranty that the reaction of the representative household entails that any change in the model will be the same as the aggregated reaction of the individuals it represents, (3) lastly, the representative household approach may interfere with the individual preferences’ weak principle.
An alternative approach is to integrate separately all individual households from a household survey directly into a CGE model, making it possible to conduct an explicit analysis of the poverty impact of macro-economic shocks on each household. The representative household problem is avoided since individual household behaviour and income distribution is directly captured without the need to impose any functional form. The first applications of this approach date to the very end of the 1990s and are reviewed in Cockburn (2006).
To illustrate the approach, this paper focuses on two specific applications – Cockburn (2006) and Cockburn et al. (2008) – which fully integrate of 3,388 and 24,797 households for Nepal and the Philippines, respectively, without sacrificing the disaggregation of factors, sectors and products required to capture the links between macro-economic shocks and poverty and income distribution.
3. Methodology
Constructing an integrated CGE micro-simulation model is technically straightforward since one merely shifts from a model with “representative” households to “real” households by integrating every household from a nationally representative household survey. As in the representative household approach, each household has an income and expenditure vector, but here these are all actual households. All the regular assumptions of a basic CGE model can be retained although, obviously, more sophisticated approaches can be envisaged. The only notable change in the CGE model code is to increase the number of households in the set defining household elements1, while the manner by which the simulations are carried out remains the same. We used variants of the EXTER model (Decaluwé et al., 2001) as the basic CGE modelling platform.
For the Philippines, labour is disaggregated into skilled and unskilled workers, both segmented into agricultural and non-agricultural labour markets. Capital and land is sector specific. For Nepal, all sectors and factors of production are separated into three regions as households: urban, Terai, and Hills/mountains. Labour is classified into skilled and unskilled. Factors are mobile between sectors within each region but not between regions. Agricultural capital is only mobile among agricultural sectors, just as non-agricultural capital is mobile between all other sectors. National production in each sector is a constant-elasticity-of-transformation (CET) combination of regional productions. As they are expected to be close substitutes, high elasticities of substitution (equal to 10) are utilized. Poverty is analysed using Foster-Greer-Thorbecke (FGT) indices (Foster et al., 1984) computed using DAD software (Duclos et al., 2001).
To implement the approach requires simply a standard Social Accounting Matrix (SAM) and data from a nationally representative household survey with complete information on household incomes and expenditures. Survey data must be adjusted to establish a link to, and ensure consistency with, the SAM underlying the CGE model. Given differences in data sources and year, it is inevitable that there will be inconsistencies in data between the SAM and the household survey. Data reconciliation is necessary to the integration process but, as it brings to light limitations or errors in one or the other datasets, it should not be seen as a “drawback” to the CGE micro-simulation approach.2
Indeed, prior data adjustment in household survey data is normally required for standard poverty/inequality analysis even outside of an integrated CGE microsimulation framework. Deaton (1997) confirms that, in household surveys, it is more difficult to collect reliable information on income than on consumption, although consumption data are not without their faults. Income underreporting and measurement errors are likely to result from the desire to hide revenues from other family members, neighbours or eventual tax authorities, as well as from the long (usually one-year) recall periods involved for intricate sources of income such as returns to assets, agricultural output and seasonal activities. This is further aggravated by the fact that most households in developing countries receive their income from informal production activities in which family income and business revenues are often combined. Thus, the absence of formal accounting in these activities and within the household make it impossible to constitute an accurate picture of the income of producer households and often lead to underestimated income (or overestimated expenditures) generated by these activities.
There is no magic recipe for reconciliation. A thorough understanding of both datasets is required and reasonable assumptions have to be made with the ultimate aim of creating a better and coherent dataset with the least possible adjustments.
The first step is to multiply the household income and expenditure vectors by their respective vectors of sample weights in order to be able to extrapolate to national values as they appear in the SAM. Furthermore, if the survey and SAM data are collected for different years, the survey data must be adjusted to account for inflation in the intervening years. A first comparison of the aggregate household income/expenditure vectors from the survey and the SAM make it possible to evaluate the magnitude and direction of divergences in each of the income and expenditure accounts. There are a variety of reasons why the two sets of vectors will not match. If the initial SAM is based on a previous household survey, it is normal that household endowments and behavior would have changed over time. If instead it is drawn solely from national accounts, the margin for divergences is even greater. Some errors may stem from survey measurement and/or sampling errors. Coverage of informal and household production activities may also vary.
The choice of which dataset to use as an anchor boils down to the modeller’s judgment. For instance, one may keep the structure of the SAM and adjust the household survey data in consequence or vice versa. If errors are suspected on both sides, a reconciliation strategy requiring some adjustments to both datasets may be required. Substantial effort should be devoted to understanding and addressing all sources of divergence. However, ultimately, some arbitrary changes will need to be made in order to ensure coherency.
In this section, we present two country cases – Nepal and the Philippines – briefly explaining the procedure employed to prepare and integrate every household from a nationally representative household survey into a SAM.
Nepal
The datasets are the 1996/97 SAM (Sapkota, 2001) and the 1995/96 Nepal Living Standards Survey (NLSS), which is based on a representative sample of 3,388 households. Due to natural inconsistencies between the two datasets, three “bridging” reconciliation rules are imposed. First, mutually inclusive variables – those present in both datasets – must be reconciled. Second, whenever a variable appears in the household survey but not in SAM (e.g. transfers between domestic households), the aggregate value from the NLSS is introduced into the SAM. Third, when the variable is in the SAM but not in the survey (for example, public transfers and dividends), its value in the survey is approximated using the SAM income or expenditure ratio.3
Net income from self-employment activities is allocated between the different factors of production, as they appear in the SAM, by imputation based on the opportunity cost of each factor (i.e. Heckman regression or simply the market wage rate, possibly corrected by the unemployment rate, in the case of labour). The revised factor income estimates are then used as the anchor and the household factor income composition in the SAM is adjusted correspondingly. As income under-reporting in the household survey leads to savings underestimation, these are instead estimated residually in the household survey after all income and expenditure adjustments have been made.
Indeed, about 45 percent of households have total income below consumption, while about 0.4 percent actually show negative incomes. Among other reasons, this could be due to: (a) a lag between income and consumption reference periods, causing consumption to be over-estimated relative to income due to inflation; (b) underestimation of incomes generated by household self-employment activities (over 91 percent of Nepalese households engage in self-employment with 46 percent of them declaring total income lower than total consumption; indeed, among households that dissave according to the NLSS, 93 percent of their incomes are generated from self-employment activities); (c) in some cases, low income levels could be accurately estimated and simply due to transitory financial difficulties experienced during the survey year.
To simultaneously address income under-reporting in the NLSS and allocate self-employment income to the various factors of production, various adjustments are applied sequentially. NLSS Step 1 (Inflation): As income is reported for the entire year, whereas expenditures are generally reported for the previous month, income is adjusted upward by half of the inflation rate (assuming a smooth distribution of income over the year).4 NLSS Step 2 (self-employment income): Self-employment income is allocated to the factors of production (land, labour and capital) used in its generation by imputing values based on their respective market opportunity costs, assuming that households will not use their resources in self-employment unless their returns are the same as renting them out. The opportunity cost of labour is computed by the mean hourly implicit wage for each socio-professional categories adjusted by their respective unemployment rates. This reflects the fact that individuals will engage in self-employment either because they cannot find paid work in their profession or their expected wage from self-employment exceeds those offered in the market. The share of returns to land from agricultural self-employment was estimated by computing the mean regional rental price of land. The value of capital share from self-employment was computed residually as the difference between net revenue and the estimated costs of all other factors used in this activity. NLSS Step 3 (negative capital income): In cases where households reported negative capital income from self-employment, this was deemed unrealistic and the values were set to zero. This correction reduced the share of households with negative savings from 40 to 26 percent. NLSS Step 4 (inter-household transfers): For all remaining household with negative savings, we assumed that this was due to the failure of the NLSS to capture intra-household transfers. Thus intransfers were increased just enough to bring savings to zero for these households, where these in-transfers are financed through a proportional increase in out-transfers from all households with positive reported savings.
Subsequently, we turn our attention to reconciling household survey and SAM data. A comparison of income and expenditure vectors from both datasets revealed that household income and expenditure in the NLSS was still understated relative to the SAM in spite of the preceding adjustments. This could be due to various causes such as the omission of households lacking information on incomes, expenditures and/or other socio-economic variables from the NLSS, as well as the 2.4 percent population growth and 7.8 percent inflation between the year of the NLSS (1995/96) and the year of theS AM (1996/97). Consequently, the income and expenditure vectors generated from the survey were increased proportionally to match SAM values. Regional savings rates rates still remained above corresponding SAM values, which we attribute to possible over-estimation of the opportunity cost of factors used in self-employment activities. These values are thus adjusted proportionally to reconcile the SAM and survey savings rates. The aggregate survey income and expenditure vectors were then substituted into the SAM and all remaining minor imbalances were corrected through a least squares SAM balancing procedure.
Philippines
The application to the Philippines uses the 1994 SAM (Cororaton, 2004) and the 1994 Family Income and Expenditure Survey (FIES), which is based on a nationally representative sample of 24,797 households. The “bridging” reconciliation rules are similar to Nepal, except that no imputation was carried out to estimate for the market equivalent prices of factors (labour and capital) used in self-employment activities. Since factor incomes and transfers for the entire family are assigned to the household head, recovering income earnings for each family member and undertaking imputation exercises on the basis of the characteristics of the household head may alter the survey structure significantly. Instead, self-employment income was directly allocated to capital income. Moreover, no adjustment for inflation was required as income and expenditure data were both collected at the same time in two rounds of visits at six months interval. Nonetheless, inter-household in-transfers were increased proportionally, as there total was inferior to total in-transfers.
Reconciliation between the household survey and the SAM was carried out in three steps. The first step involved proportionally increasing the expenditure vector in the SAM as it was six percent below that of the household survey. This difference was attributed to inter-household transfers, which are non-existent in the initial SAM. The second adjustment was on total labour income and total capital income, which are, respectively, 40 and 38 percent higher in the SAM. Since both datasets are for the same year, this reconciliation process was straightforward with survey values normalized to SAM totals, implying that capital and labour income for each household was increased proportionally. Finally, savings was computed residually.
4. Applications and simulation results
To illustrate the integrated CGE microsimulation approach, we study the impact, in both Nepal and the Philippines, of the elimination of all import tariffs with a compensatory uniform consumption tax designed to maintain government revenue constant.5 As the consumption tax is applied uniformly to all goods, it does not create any distortions in the relative consumer prices, allowing us to focus on the impacts of the elimination of all tariffs. We present the results in terms of sectoral supply and demand, factor returns, household income and consumption, and finally poverty, bearing in mind that in a CGE model all variables interact and are determined simultaneously. We first discuss the simulation results for the Philippines then proceed with the discussion for Nepal.
Philippines
The elimination of tariffs affects the agricultural and industrial sectors differently (Table 1). Since import-weighted average tariff rates are higher in agriculture, import prices (PM) fall more, and import volumes (M) increase proportionately more in agriculture than in industry. However, as import competition (intensity) is greater in the industrial sector, domestic prices for locally-produced goods (PD and, net of taxes, PL) and consumer prices (PQ) fall more in the industrial sector, whereas they rest almost constant for services, which are not imported. At the same time, faced with a fixed current account balance, rising imports lead to a real exchange rate devaluation and an expansion in exports. Industrial exports (EX) expand more than agricultural and service exports since industry is more export-oriented. Industry also benefits more from falling imported input costs which, together with the depreciating real exchange rate, make domestic industrial products more competitive in the international market. The net impact is a slight reduction in output (XS) in the inward oriented agricultural sector in favour of the service sector and the outward oriented industrial sector. Output prices (PX) also fall less in industry than in agriculture, despite the greater reduction in prices for domestic sales (PL), given industry’s greater export intensity, where export prices are assumed to be constant.
Effects of trade liberalization on sectors, Philippines (% change).
| Price | Volume | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SECTORS | PM | PQ | PD | PL | PX | M | EX | D | Q | XS |
| Irrigated Paddy | −31.0 | −5.0 | −5.0 | −8.2 | −8.2 | 395.0 | − | −1.8 | −1.8 | −1.8 |
| Non irrigated Paddy | − | −5.8 | −5.8 | −9.0 | −9.0 | − | − | −1.6 | −1.6 | −1.6 |
| Corn | −33.9 | −7.0 | −5.3 | −8.4 | −8.4 | 53.2 | 7.6 | −4.1 | −1.7 | −4.0 |
| Banana | − | −6.3 | −6.3 | −9.4 | −3.9 | − | 22.7 | 2.2 | 2.2 | 14.0 |
| Fruits | −39.6 | −7.8 | −4.7 | −7.9 | −6.9 | 126.3 | 13.5 | −2.5 | 3.6 | −0.5 |
| Coconut | − | −4.3 | −4.3 | −7.5 | −6.7 | − | 18.8 | 2.9 | 2.9 | 4.5 |
| Sugarcane | − | −6.9 | −6.9 | −10.0 | −10.0 | − | − | −7.2 | −7.2 | −7.2 |
| Other agricultural crops | −16.3 | −4.5 | −4.3 | −7.5 | −6.9 | 51.7 | 26.2 | −1.8 | −1.1 | −0.1 |
| Hog | −32.8 | −7.4 | −5.5 | −8.6 | −8.6 | 88.9 | − | −4.6 | −0.5 | −4.6 |
| Chicken, eggs & poultry products | −12.0 | −4.2 | −4.1 | −7.3 | −7.3 | 17.0 | 14.7 | −1.5 | −1.4 | −1.5 |
| Other livestock | −24.1 | −5.4 | −5.3 | −8.4 | −8.4 | 38.6 | 12.9 | −1.3 | −1.1 | −1.3 |
| Fishing | −9.8 | −2.4 | −2.4 | −5.7 | −4.5 | 10.5 | 7.8 | 0.2 | 0.2 | 1.8 |
| Other Agriculture | 3.5 | −3.2 | −3.5 | −6.7 | −6.7 | −20.7 | − | 0.2 | −0.6 | 0.2 |
| AGRICULTURE | −25.7 | −5.0 | −4.4 | −7.6 | −7.0 | 66.2 | 13.9 | −1.7 | −0.6 | −0.5 |
| Mining | −6.8 | −5.9 | −3.0 | −6.3 | −3.3 | 6.6 | 24.4 | −17.4 | 0.3 | 0.9 |
| Meat Processing | −34.3 | −8.6 | −6.3 | −9.4 | −9.4 | 314.6 | 42.4 | −5.8 | 4.7 | −5.5 |
| Canning/preserving of fruits & veg. | −26.0 | −4.9 | −3.5 | −6.8 | −4.7 | 66.7 | 12.9 | −1.8 | 1.1 | 2.5 |
| Fish canning and processing | −29.5 | −1.2 | −0.6 | −3.9 | −2.3 | 330.9 | 13.5 | −4.8 | −2.1 | 2.5 |
| Coconut processing | −29.6 | −12.5 | −7.0 | −10.1 | −3.6 | 58.8 | 12.5 | −9.0 | 2.9 | 4.6 |
| Rice and corn milling | −31.0 | −3.6 | −2.9 | −6.2 | −6.2 | 139.1 | 16.0 | −1.7 | 0.0 | −1.7 |
| Sugar milling and refining | −40.4 | −10.4 | −5.5 | −8.7 | −7.8 | 211.3 | 15.0 | −10.0 | 3.9 | −7.7 |
| Beverages, Sugar, Confectionery | −15.5 | −3.7 | −3.1 | −6.3 | −6.1 | 20.5 | 8.8 | −0.8 | 0.0 | −0.5 |
| Other food manufacturing | −16.6 | −6.5 | −3.8 | −7.0 | −6.6 | 33.9 | 13.3 | −5.0 | 1.7 | −3.9 |
| Textile and garments | −23.5 | −16.5 | −9.5 | −12.6 | −5.8 | 52.7 | 34.8 | −19.0 | 10.0 | 7.4 |
| Wood and paper products | −16.5 | −11.0 | −6.9 | −10.0 | −6.9 | 24.7 | 23.1 | −11.7 | 1.8 | −1.8 |
| Fertilizer | 3.0 | 2.5 | 1.7 | −1.7 | −1.0 | −1.7 | 8.4 | 2.4 | −0.3 | 5.0 |
| Other chemicals | −11.0 | −8.5 | −6.2 | −9.3 | −8.0 | 11.2 | 28.9 | −6.6 | 1.7 | −2.2 |
| Petroleum related products | −1.5 | −1.5 | −1.5 | −4.8 | −4.5 | −0.6 | 10.1 | −0.7 | −0.7 | 0.0 |
| Metal and related products | −11.3 | −8.7 | −5.0 | −8.1 | −4.2 | 13.8 | 20.6 | −11.4 | 2.5 | 3.0 |
| Semi-conductors & other electronic | −8.9 | −7.4 | −3.4 | −6.7 | −1.8 | 13.3 | 19.0 | −12.1 | 5.7 | 10.1 |
| Motor vehicles & other machineries | −7.6 | −6.9 | −4.8 | −7.9 | −4.9 | 5.3 | 27.7 | −6.0 | 2.1 | 6.0 |
| Other manufacturing | −26.1 | −18.7 | −11.0 | −14.0 | −9.0 | 46.5 | 30.3 | −22.2 | 5.8 | −5.6 |
| Construction and utilities | 0.0 | −3.2 | −3.2 | −6.4 | −6.3 | − | 14.5 | −1.9 | −1.9 | −1.7 |
| INDUSTRY | −11.6 | −7.3 | −4.6 | −7.8 | −5.9 | 18.5 | 23.5 | −6.3 | 1.9 | 0.2 |
| Wholesale trade | − | −0.4 | −0.4 | −3.7 | −2.9 | − | 5.9 | −1.5 | −1.5 | 0.1 |
| Other service | − | −0.2 | −0.2 | −3.6 | −3.0 | − | 6.4 | −0.7 | −0.7 | 0.4 |
| Government services | − | − | − | − | −3.8 | − | − | − | − | − |
| SERVICES | − | −0.3 | −0.3 | −3.6 | −3.0 | − | 6.2 | −1.0 | 0.3 | 0.3 |
-
Key: PM = import prices; PQ = composite consumer prices; PD = prices of local goods sold on the domestic market (with tax); PL = prices of local goods sold on the domestic market (without tax); PX = composite (export-domestic) producer prices; M = imports; EX = exports; D = domestic sales; Q = composite commodity; XS = total output; “-”- zero at the base.
However, it is value added prices that drive factor returns and, eventually, income and poverty effects. Falling output prices bring a general reduction in both nominal returns to capital (R) and the average wage rate (Table 2). Greater input cost savings imply that value added priced (PVA) fall even less in industry relative to agriculture. The service sector, which is unaffected by import tariff liberalization, emerges with the smallest reduction in value added prices. As a result, returns to capital fall more in agriculture than in industry and services, and agricultural wages fall more than wages for non-agricultural workers.
Effects of trade liberalization on factors, Philippines (% change).
| Value Added | Labour Demand | ||||||
|---|---|---|---|---|---|---|---|
| SECTORS | VA | PVA | R | Total Labour | Agriculture | Un-skilled Non-Agriculture | Skilled Non-Agriculture |
| Irrigated Paddy | −1.8 | −10.2 | −11.8 | −3.5 | −3.3 | −8.2 | −9.0 |
| Non irrigated Paddy | −1.6 | −9.5 | −10.9 | −2.5 | −2.3 | −7.2 | −8.1 |
| Corn | −4.0 | −9.8 | −13.4 | −5.8 | −5.0 | −9.8 | −10.7 |
| Banana | 14.0 | −4.4 | 8.9 | 18.3 | 19.4 | 13.4 | 12.4 |
| Fruits | −0.5 | −8.3 | −8.7 | −0.9 | 0.1 | −4.9 | −5.8 |
| Coconut | 4.5 | −7.5 | −3.3 | 5.2 | 6.0 | 0.7 | −0.3 |
| Sugarcane | −7.2 | −13.5 | −19.8 | −12.3 | −12.0 | −16.4 | −17.2 |
| Other agricultural crops | −0.1 | −8.2 | −8.2 | −0.3 | 0.6 | −4.4 | −5.3 |
| Hog | −4.6 | −11.4 | −15.4 | −8.4 | −7.3 | −11.9 | −12.8 |
| Chicken, egg & poultry products | −1.5 | −9.2 | −10.6 | −3.0 | −1.9 | −6.9 | −7.7 |
| Other livestock | −1.3 | −10.1 | −11.2 | −3.7 | −2.6 | −7.5 | −8.4 |
| Fishing | 1.8 | −4.7 | −3.0 | 5.0 | 6.4 | 1.0 | 0.1 |
| Other Agriculture | 0.2 | −7.8 | −7.6 | 0.2 | 1.3 | −3.8 | −4.7 |
| AGRICULTURE | −0.4 | −8.4 | −8.5 | −0.8 | 0.0 | −4.4 | −5.1 |
| Mining | 0.9 | −2.5 | −1.6 | 2.0 | − | 2.5 | 1.6 |
| Meat Processing | −5.5 | −18.7 | −23.2 | −20.4 | − | −20.0 | −20.7 |
| Canning/preserving of fruits & veg. | 2.5 | −0.6 | 1.9 | 5.7 | − | 6.1 | 5.2 |
| Fish canning and processing | 2.5 | −0.2 | 2.3 | 6.1 | − | 6.5 | 5.5 |
| Coconut processing | 4.6 | 1.7 | 6.3 | 10.1 | − | 10.7 | 9.7 |
| Rice and corn milling | −1.7 | −8.8 | −10.4 | −7.1 | − | −6.7 | −7.5 |
| Sugar milling and refining | −7.7 | −11.8 | −18.6 | −15.6 | − | −15.2 | −16.0 |
| Beverages, Sugar, Confectionery | −0.5 | −4.3 | −4.8 | −1.3 | − | −0.9 | −1.8 |
| Other food manufacturing | −3.9 | −7.9 | −11.5 | −8.3 | − | −7.8 | −8.7 |
| Textile and garments | 7.4 | 6.8 | 14.7 | 18.8 | − | 19.4 | 18.3 |
| Wood, and paper products | −1.8 | −6.2 | −7.8 | −4.5 | − | −4.0 | −4.9 |
| Fertilizer | 5.0 | 8.9 | 14.4 | 18.5 | − | 19.1 | 18.0 |
| Other chemicals | −2.2 | −9.2 | −11.2 | −7.9 | − | −7.6 | −8.4 |
| Petroleum related products | 0.0 | −3.7 | −3.7 | −0.1 | − | 0.3 | −0.7 |
| Metal and related products | 3.0 | 3.3 | 6.4 | 10.3 | − | 10.8 | 9.8 |
| Semi-conductors & other electronic | 10.1 | 13.9 | 25.4 | 29.9 | − | 30.5 | 29.3 |
| Motor vehicles and other machineries | 6.0 | 4.6 | 10.9 | 14.9 | − | 15.5 | 14.4 |
| Other manufacturing | −5.6 | −9.5 | −14.5 | −11.4 | − | −11.0 | −11.8 |
| Construction and utilities | −1.7 | −6.3 | −8.0 | −4.5 | − | −4.2 | −5.0 |
| INDUSTRY | −0.2 | −4.3 | −4.5 | −0.3 | 0.0 | −0.2 | 0.02 |
| Wholesale trade | 0.1 | −3.7 | −3.6 | 0.2 | − | 0.4 | −0.5 |
| Other service | 0.4 | −2.4 | −2.0 | 1.4 | − | 2.0 | 1.1 |
| Government services | 0.0 | −4.0 | 0.0 | 0.0 | − | − | − |
| SERVICES | 0.3 | −2.8 | −2.5 | 0.9 | 0.0 | 1.0 | 1.0 |
| TOTAL | −0.1 | −4.5 | −4.1 | ||||
| Change in average wage, % --> | −4.7 | −8.8 | −4.0 | −3.1 | |||
-
Key: VA = value added; PVA = value added prices; R = rate of return to capital; “-”– zero at the base.
-
Notes: The changes in labour demand volume for skilled and unskilled agricultural labour in the agricultural sectors are the same. This is because in the SAM, all agricultural sectors have the same share of skilled and unskilled agricultural labour (18 and 82 percent share in total agriculture labour respectively) in production—owing to absence of data to break detailed agriculture labour across agricultural sub-sectors. Nonetheless, this does not significantly affect the computational results of the model.
Obviously, total nominal household income falls across all household categories (Table 3) due to the fall in both nominal wages and returns to capital. The decomposition in Table 3 shows that this income fall is driven primarily by the reduction in wage income, particularly among non-agricultural skilled workers, who contribute a high share in total household income, and agricultural workers, who are hardest hit by the wage reductions outlined in Table 2. Given their reliance on agricultural income, income reduction among male headed households is stronger, when compared to their female counterparts. Similarly, less educated households experience greater nominal income losses than their higher-educated counterparts.
Effects of trade liberalization on household income, Philippines (% change).
| Female | Male | |||||||
|---|---|---|---|---|---|---|---|---|
| Factors | Household categories | All | All | Low Educated | High Educated | All | Low Educated | High Educated |
| Agriculture Skilled | −0.2 | −0.1 | − | −0.1 | −0.2 | − | −0.4 | |
| Agriculture Unskilled | −0.6 | −0.3 | −0.7 | − | −0.7 | −1.5 | − | |
| Non-agriculture Skilled | −0.9 | −0.7 | − | −1.3 | −0.9 | − | −1.7 | |
| Non-agriculture Unskilled | −0.4 | −0.5 | −1.0 | − | −0.4 | −0.9 | − | |
| Labour | Total Labour | −2.1 | −1.5 | −1.7 | −1.4 | −2.2 | −2.4 | −2.1 |
| Agriculture | −0.7 | −0.4 | −0.7 | −0.2 | −0.8 | −1.3 | −0.3 | |
| Industry | −0.1 | −0.1 | −0.1 | 0.0 | −0.1 | −0.1 | −0.1 | |
| Services | −0.6 | −0.6 | −0.6 | −0.6 | −0.6 | −0.5 | −0.7 | |
| Land | −0.2 | −0.1 | −0.1 | 0.0 | −0.2 | −0.3 | −0.1 | |
| Capital | Total Capital | −1.6 | −1.2 | −1.5 | −0.9 | −1.6 | −2.1 | −1.2 |
| Other | Dividends | − | − | − | − | − | − | − |
| Income | Others | − | − | − | − | − | − | − |
| Total | −3.7 | −2.7 | −3.2 | −2.2 | −3.9 | −4.5 | −3.3 | |
-
Notes: (a) “-” in labour income block indicates the absence of household income from the corresponding labour type. For instance, low (high) educated male and female have no labour income from skilled (unskilled) agriculture labour and skilled (unskilled) non-agriculture labour. (b) “-” in the Other income block is due to the assumption that non-factor income (i.e., dividends, government transfers and remittances) are held fixed to prevent any possible welfare/poverty effects of variations from these income sources; (c) “Total” shows over-all variation in income. This is calculated as the sum of contribution of each income source to the total variation in income.
On average, consumer prices fall more than nominal household incomes (Table 4). This is not the case in rural areas, where nominal incomes fall more given the above-noted strong reductions in the returns to agricultural factors. This impact can be traced primarily to households headed by low educated males, for whom nominal incomes fall more than consumer prices, as they are the most dependent on agricultural income.
Effects of trade liberalization on income and prices, Philippines (% change).
| All | All Female | Low Educated Female | High Educated Female | All Male | Low Educated Male | High Educated Male | |
|---|---|---|---|---|---|---|---|
| Income | |||||||
| All Philippines | −3.7 | −2.7 | −3.2 | −2.2 | −3.9 | −4.5 | −3.3 |
| NCR | −2.7 | −2.3 | −2.4 | −2.3 | −2.8 | −2.5 | −2.9 |
| Urban except NCR | −3.3 | −2.4 | −2.8 | −2.1 | −3.4 | −3.8 | −3.2 |
| Rural | −4.9 | −3.7 | −4.1 | −2.6 | −5.1 | −5.5 | −4.2 |
| Consumer price index per household category | |||||||
| All Philippines | −4.2 | −3.7 | −3.9 | −3.3 | −4.2 | −4.1 | −4 |
| NCR | −3.6 | −3.3 | −3.5 | −2.5 | −3.7 | −3.3 | −3.5 |
| Urban except NCR | −4.2 | −3.8 | −3.9 | −3.5 | −4.3 | −4.5 | −4 |
| Rural | −4.4 | −4.1 | −4.2 | −3.7 | −4.5 | −4.5 | −4.4 |
-
Notes: (a) Consumer price index per household category is the same as the Weighted Price of Household Specific Consumer Basket; (b) NCR stands for National Capital Region, otherwise known as Metro Manila, which is the capital of the Philippines.
These income and consumer price changes can be traced to each individual household from the FIES in order to analyze the poverty impacts. Overall, the national poverty headcount index falls marginally, whereas both the national poverty gap and severity index increase marginally, implying that the poor become even poorer (Table 5). Indeed, the poor are overwhelmingly concentrated in rural areas and thus hit hardest by the fall in agricultural income. A clear pro-urban bias in the poverty results emerges as all poverty indices fall significantly in the National Capital region and compare favourably among other urban households relatively to rural households, for whom all poverty indices increase. Households with highly educated heads also benefit more from tariff reductions than their counterparts with low educated heads, given their greater relative reliance on non-factor and non-agricultural income and skilled wages. Moreover, poverty falls dramatically among households headed by highly educated females given their high share of income from non-factor and non-agricultural sources. As the underlying data is available at the individual household level, analysis by other socio-economic categories would, of course, straightforward.
Effects of trade liberalization on poverty, Philippines (% change).
| FGT Poverty Index | All | All Female | Low Educated Female | High Educated Female | All Male | Low Educated Male | High Educated Male |
|---|---|---|---|---|---|---|---|
| All Philippines | |||||||
| Headcount | −0.2 | −2.9 | −2.5 | −5.9 | 0.0 | 0.1 | −0.6 |
| Gap | 0.8 | −1.3 | −1 | −4.3 | 0.9 | 1.1 | 0 |
| Severity | 1.2 | −1.2 | −0.9 | −3.5 | 1.4 | 1.6 | 0.3 |
| National Capital Region (NCR) | |||||||
| Headcount | −1.6 | −6.3 | −5.1 | −9.1 | −1 | −2.6 | 0.8 |
| Gap | −2.5 | −3.5 | −3.4 | −4.5 | −2.4 | −2.8 | −2 |
| Severity | −3.2 | −4.2 | −4.4 | −4.8 | −2.9 | −3.5 | −2 |
| All Urban Households (except NCR) | |||||||
| Headcount | −0.7 | −3.1 | −2.7 | −5.7 | −0.5 | −0.1 | −1.7 |
| Gap | 0.2 | −2.5 | −2.1 | −5.7 | 0.4 | 0.6 | −0.7 |
| Severity | 0.7 | −2.3 | −2 | −5.8 | 0.9 | 1.2 | −0.3 |
| All Rural Households | |||||||
| Headcount | 0.0 | −2.6 | −2.3 | −5.3 | 0.2 | 0.3 | −0.03 |
| Gap | 1.1 | −0.8 | −0.6 | −3.6 | 1.2 | 1.3 | 0.6 |
| Severity | 1.5 | −0.7 | −0.5 | −2.7 | 1.7 | 1.8 | 0.8 |
-
Notes: Poverty headcount – Proportion of the population that falls below the poverty line; Poverty gap – Indicates how far on the average the poor are from the poverty line; Poverty-severity – Squared average distance of income of the poor from the poverty line.
Nepal
Sectoral supply and demand effects of trade liberalization in Nepal are presented in Table 6. As in the Philippines, the sectors with high initial tariff rates (TM) – paddy, other food crops, mining, and gas/electricity/water – experience the greatest increase in import volumes. The impact of this increase in import volume is tempered however, as imports represent a small share of local consumption in all sectors, except manufacturing and, to a lesser degree, the transport/communication, mining and trade sectors.
Effects of trade liberalization on sectoral production, Nepal (% change).
| Tariff rate | Import volumes | Exports and Production | Value Added | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TM | M | M/Q | D | PD | EX | EX/XS | XS | PX | Urban | Terai | Hills | |
| AGRICULTURE | ||||||||||||
| Paddy | 13.5 | 52.4 | 0.2 | −0.8 | −4.0 | 21.6 | 0.1 | −0.7 | −4.0 | −0.7 | −0.5 | −1.4 |
| Other food crops | 12.2 | 43.4 | 0.6 | −0.8 | −4.0 | 21.9 | 0.2 | −0.8 | −4.0 | 0.8 | 0.4 | −1.7 |
| Cash crops | 7.0 | 11.7 | 3.5 | −0.7 | −4.3 | 23.8 | 2.0 | −0.2 | −4.2 | −1.3 | −0.8 | 0.4 |
| Livestock/fisheries | 4.4 | −1.5 | 1.2 | −0.9 | −4.4 | 24.0 | 1.9 | −0.4 | −4.3 | −1.0 | −0.9 | 0.0 |
| Forestry | 0.8 | −4.2 | 25.1 | 0.1 | 0.9 | −4.2 | −0.5 | 0.6 | 1.6 | |||
| NON-AGRICULTURE | ||||||||||||
| Mining | 12.3 | 39.8 | 8.6 | −10.4 | −2.6 | −10.4 | −2.6 | −12.2 | −11.8 | −9.8 | ||
| Manufacturing | 8.1 | 15.8 | 47.0 | −8.1 | −3.1 | 7.8 | 16.8 | −5.4 | −2.6 | −6.0 | −5.4 | −3.5 |
| Construction | −0.9 | −2.4 | −0.9 | −2.4 | −1.2 | −0.7 | −0.6 | |||||
| Gas, electricity, water | 10.9 | 47.7 | 2.4 | −2.3 | −2.0 | −2.3 | −2.0 | −2.4 | −1.9 | −1.9 | ||
| Hotel and restaurant | 1.6 | −2.4 | 14.9 | 55.9 | 9.1 | −1.0 | 9.2 | 10.1 | 6.6 | |||
| Transport/communication | 6.0 | 13.8 | 13.3 | −1.4 | −2.9 | 14.4 | 30.5 | 3.5 | −2.0 | 3.4 | 4.0 | 3.0 |
| Trade | 3.4 | 2.2 | 6.8 | 1.5 | −3.1 | 18.9 | 20.9 | 5.2 | −2.4 | 3.2 | 6.4 | 10.0 |
| Banking and real estate | 0.9 | −2.1 | 0.9 | −2.1 | 0.5 | 1.6 | 0.5 | |||||
| Government services | −0.1 | −2.5 | −0.1 | −2.5 | −0.1 | −0.3 | 0.3 | |||||
| Other services | −0.1 | −2.2 | 11.6 | 0.8 | 0.0 | −2.2 | 1.6 | 0.2 | −2.7 | |||
-
Key: TM = initial tariff rate; δ = variation; M = Imports; Q = domestic consumption; M/Q = import penetration rate; D = Local sales of domestic output; PD = Price of local sales of domestic output; EX = exports; XS = domestic output; EX/XS = export intensity ratio; PX = Producer price of composite domestic output; VA = value added.
-
Notes: Changes in value added and Output are equal.
In general, the export-oriented sectors – hotel/restaurant, transport/communication and trade – post the greatest output increases. Manufacturing exports are insufficient to offset the sector’s vulnerability to import competition (47 percent of local consumption) such that it posts the greatest output contraction next to mining, which does not export at all. The agricultural sector has very low export intensities, 2 percent or less, and thus posts output contractions and the greatest reduction in producer prices.
The fall in agricultural producer prices translates into a reduction in the remuneration of factors used intensively in agriculture, namely land, unskilled labour and agricultural capital (Table 7). Note that unskilled wages in the agricultural sector falls by about 4 percent, which is roughly as much as the fall in the prices of agricultural output. In contrast, the decline is smaller for urban unskilled labour as it is not so tightly linked to the agricultural sector.
Effects of trade liberalisation on factor remuneration, Nepal (% change).
| Wage Rate | Returns to: | |||||
|---|---|---|---|---|---|---|
| Unskilled | Skilled | Capital in Agriculture | Capital in Non-agriculture | Land | Other income | |
| Urban | −2.9 | −2.3 | −5.4 | −1.7 | −5.4 | 0.02 |
| Terai | −4.1 | −2.3 | −5.1 | −0.6 | −5.1 | 0.02 |
| Hills and Mountains | −4.3 | −2.3 | −4.4 | −0.8 | −4.4 | 0.02 |
For a better understanding of the household income impacts, the average income changes for households in each region are decomposed into changes in income from each factor (Table 8). Since Terai and Hill/mountain households derive their income primarily from unskilled labour and land, households in these two regions have a more substantial loss (3.3 percent) in nominal income than urban households (1.8 percent). In contrast, urban households earn nearly one-third of their income from non-agricultural capital and nearly a quarter more from skilled wages, which are the two factors that experience the smallest reductions in terms of remuneration rates. These changes imply that, on the income side, trade liberalization favours urban households over rural households.
Sources of household income by region, Nepal.
| Income shares (%) | Change in factor Remuneration rates (%) | Income changes (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Urban | Terai | Hills | Urban | Terai | Hills | Urban | Terai | Hills | |
| WAGES | |||||||||
| Unskilled | 24.5 | 33.8 | 36.1 | −2.9 | −4.1 | −4.3 | −0.7 | −1.4 | −1.6 |
| Skilled | 22.0 | 10.4 | 9.2 | −2.3 | −2.3 | −2.3 | −0.5 | −0.2 | −0.2 |
| RETURNS TO: | |||||||||
| Agricultural Capital | 0.4 | 1.9 | 1.8 | −5.4 | −5.1 | −4.4 | 0.0 | −0.1 | −0.1 |
| Non-agricultural Capital | 32.5 | 18.8 | 11.6 | −1.7 | −0.6 | −0.8 | −0.6 | −0.1 | −0.1 |
| Land | 3.2 | 30.5 | 34.1 | −5.4 | −5.1 | −4.4 | −0.3 | −1.6 | −1.5 |
| OTHER INCOME | 14.3 | 4.7 | 7.1 | 0.0 | 0.0 | 0.0 | 0.3 | 0.1 | 0.1 |
| TOTAL | 100.0 | 100.0 | 100.0 | −1.8 | −3.3 | −3.3 | |||
At the same time, trade liberalization affects consumer prices (Table 9) through the reduction in import prices and, in the face of this import competition, in the prices of local sales by domestic producers. At the same time, a uniform compensatory consumption tax is introduced to keep government revenue constant, which raises consumer prices proportionally in all sectors. Generally speaking, consumer prices fall most in the initially highly protected sectors – paddy, other food crops, mining and gas/electricity/water sectors – and the initially moderately protected but import-intensive manufacturing sector.
Effects of trade liberalization on consumer prices, Nepal (% change).
| PM | PD | M/Q | PC | Urban | Terai | Hills / Mountains | |
|---|---|---|---|---|---|---|---|
| AGRICULTURE | 65.0 | 79.2 | 79.0 | ||||
| Paddy | −11.9 | −4.0 | 0.2 | −3.0 | 14.1 | 32.1 | 18.2 |
| Other food crops | −10.9 | −4.0 | 0.6 | −3.1 | 5.9 | 13.5 | 18.1 |
| Cash crops | −6.5 | −4.3 | 3.5 | −3.4 | 24.1 | 24.2 | 28.8 |
| Livestock/fisheries | −4.2 | −4.4 | 1.2 | −3.4 | 4.4 | 4.0 | 5.0 |
| Forestry | −4.2 | −4.2 | 1.2 | −3.2 | 16.5 | 5.4 | 8.8 |
| Mining | −10.9 | −2.6 | 8.6 | −2.5 | 0.0 | 0.0 | 0.0 |
| NON-AGRICULTURE | 35.0 | 20.8 | 21.0 | ||||
| Manufacturing | −7.5 | −3.1 | 47.0 | −3.7 | 19.5 | 13.2 | 15.1 |
| Construction | 0.0 | −2.4 | 0.0 | −1.4 | 0.0 | 0.0 | 0.0 |
| Gas, electricity, water | −9.8 | −2.0 | 2.4 | −1.2 | 0.5 | 0.1 | 0.0 |
| Hotel and restaurant | 0.0 | −2.4 | 0.0 | −1.4 | 0.3 | 0.1 | 0.1 |
| Transport/communication | −5.7 | −2.9 | 13.3 | −2.2 | 2.9 | 1.1 | 1.1 |
| Trade | −3.2 | −3.1 | 6.8 | −2.1 | 0.0 | 0.0 | 0.0 |
| Banking and real estate | 0.0 | −2.1 | 0.0 | −1.1 | 0.2 | 0.5 | 0.1 |
| Government services | 0.0 | −2.5 | 0.0 | −1.4 | 10.0 | 5.0 | 4.0 |
| Other services | 0.0 | −2.2 | 0.0 | −1.1 | 1.6 | 0.8 | 0.6 |
| Total | 100 | 100 | 100 | ||||
| Consumer price indices | −3.1 | −3.1 | −3.2 |
-
Key: PM = Price of imports; PD = Price of local sales of domestic output; M/Q = import penetration rate; PC = Consumer prices
What conclusions can we draw in terms of poverty? Making full use of the household-level results, it is possible to draw curves showing the variation in headcount ratios and the poverty gap (Figures 1 and 2) over a wide range of poverty lines (from zero to twice the median income). This gives us a much more detailed view of how the impacts of trade liberalization vary over the whole income distribution. These figures show that results are very sensitive to the choice of poverty line. While there is some evidence of a slight reduction in the number of the very poorest (under 900 rupees, or $US 43, per capita annual income), the number of moderately poor increases as a result of trade liberalisation (Figure 1). Similar results are obtained in terms of the poverty gap, with the very richest clearly emerging as beneficiaries of trade liberalization (Figure 2).
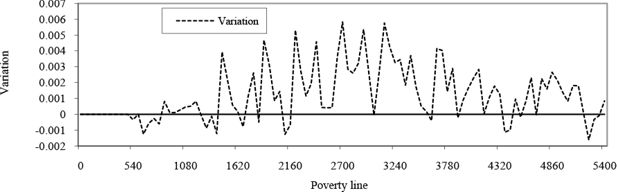
Variation in headcount ratio curves, Nepal (All regions).
Note: This figure represents the variation in the headcount ratio resulting from trade liberalisation for a whole range of poverty line.
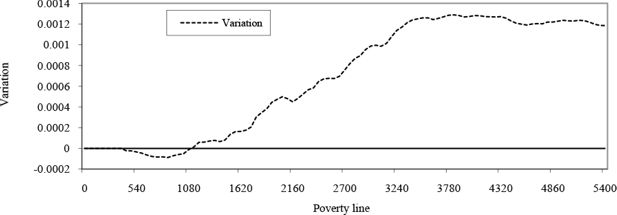
Variation in poverty gap curves, Nepal (All regions).
Notes: This figure represents the variation in the poverty gap resulting from trade liberalisation for a whole range of poverty lines.
This analysis can be pushed further to examine the impacts among particular socio-economic or regional groups. In results not shown here, the incidence of poverty in urban areas is found to fall, whereas it increases in the two rural areas. Indeed, the urban poor have a greater endowment of non-agricultural capital and depend less on income from land and unskilled labour. Here, too, it is possible to go further into the analysis to contrast, for example, impacts on the extreme versus moderate poor.
5. Conclusion
This paper has shown how to explicitly integrate into a CGE model each household from a nationally representative household survey to overcome the representative household critique. To the extent that the analysis of macro-economic shocks has differing impacts on individual households, an explicit analysis that integrates household-level income sources and consumption patterns is essential.
We have also shown that constructing a standard integrated CGE micro-simulation model is straightforward, since one merely shifts from a model with several “representative” households to a model with a large number of “real” households. Practically no modification is required to the standard CGE model code and the only data requirements are the SAM and other data underlying a standard model and a recent household survey containing complete income and expenditure data.
The main challenge of this approach is to reconcile the national accounts and household survey data. However, reconciliation is just as necessary in the representative household and sequential microsimulation approaches presented in the other papers of this volume, even if it is often ignored. There is no magic recipe for reconciliation; a thorough understanding of the datasets are required and reasonable assumptions must be made, with the ultimate aim of creating a more reliable and coherent database with minimal data alteration.
Through applications to Nepal and the Philippines, we have shown how this approach can generate rich and nuanced insights into the full distributive impacts of trade liberalization and other macro shocks. A rich agenda for future research remains, particularly in integrating some of the more sophisticated labour market modelling found in sequential CGE microsimulation models. Another extension could be in terms of modelling the motors of growth in order to explicitly identify how each household is affected by and contributes to growth.
Footnotes
1.
For instance, moving from a CGE model with three representative households to a fully integrated version with 5000 household only entails changes in a slice of code. That is, (a) In GAMS, the household SET H previously defined as SET h/h1*h3/ will be modified to SET h/h1*h5000/; (b) In GEMPACK, one moves from SET H (h1-h3) to SET H (h1-h5000).
2.
Refer to Cockburn and Cloutier (2002) for a detailed discussion of the different techniques available.
3.
See Fofana and Cockburn (2003) for a technical description of reconciliation procedure.
4.
Paxson (1992) adjusts household savings by deflating household consumption by the inflation rate over the period of the survey.
5.
Although complete tariff elimination may not be implemented by both countries in the near future, it provides an order of magnitude and allows us to compare the impacts of trade liberalization on Nepal and the Philippines in a consistent manner.
References
-
1
Income Distribution Policy: A Computable General Equilibrium Model of South KoreaStanford: Stanford University Press.
-
2
Poverty, income distribution and cge modeling: does the functional form of distribution matter?. Cahier 03-32Montreal: CIRPEE, Université Laval.
-
3
Conclusion: Where do we go from here?In: F Bourguignon, LA Pereira da Silva, editors. The Impact of Economic Policies on Poverty and Income Distribution: Evaluation Techniques and Tools. New York: World Bank and Oxford University Press. pp. 339–349.
-
4
Trade liberalisation and poverty in Nepal: a computable general equilibrium micro simulation analysisIn: M Bussolo, J Round, editors. Globalization and Poverty: Channels and Policies. London: Routledge. pp. 171–194.
-
5
Poverty effects of the Philippines’ Tariff Reduction Program: Insights from a CGE modelAsian Economic Journal 22:287–317.
-
6
How to build an integrated CGE microsimulation model : step-by-step instructions with an illustrative exercisemimeo, Poverty and Economic Policy (PEP) research network, www.pep-net.org/fileadmin/medias/pdf/microsim.pdf.
-
7
Growth distribution and poverty in Madagascar: learning from a microsimulation model in a general equilibrium framework. TMD Discussion Paper 61Washington, D.C.: International Fool Policy Research Institute.
-
8
Analyzing the impact of trade reforms on welfare and income distribution using cge framework: the case of the philippinesPhilippine Journal of Development 57:25–64.
-
9
Measuring poverty and inequality in a computable general equilibrium model. Working paper 99-20Quebec: Centre de recherche en économie et finance appliquées (CREFA), Université Laval.
-
10
La politique économique du développement et les modèles d’équilibre général calculableMontréal: University of Montreal press.
-
11
Politically feasible and equitable adjustment: some alternatives for EcuadorWorld Development 19:1577–1594.
-
12
The analysis of household surveys: a microeconometric approach to development policyBaltimore: Johns Hopkins University Press for the World Bank.
-
13
General Equilibrium Models for Development PolicyCambridge: Cambridge University Press.
-
14
MIMAP ProgrammeMIMAP Programme, International Development Research centre, Government of Canada and CREFA, Université Laval, Montreal.
-
15
Microsimulations in Computable General Equilibrium: Procedures for analysing and reconciling dataMicrosimulations in Computable General Equilibrium: Procedures for analysing and reconciling data, mimeo, Poverty and Economic Policy (PEP) research network, www.pep-net.org/fileadmin/medias/pdf/Reconciliation.pdf.
- 16
-
17
Predicting the poverty impacts of trade reformThe Journal of International Trade and International Development 14:377–405.
-
18
Whom or what does the representative individual represent?Journal of Economic Perspectives 6:117–136.
-
19
Poverty and inequality analysis in a general equilibrium framework: the representative household approachIn: F Bourguignon, AL Pereira da Silva, editors. The Impact of Economic Policies on Poverty and Income Distribution: Evaluation Techniques and Tools. Washington D.C.: The World Bank. pp. 325–339.
-
20
The general equilibrium income distribution modelIn: L Taylor, EL Bacha, EA Cardoso, F Lysy, editors. Models of Growth and Distribution for Brazil. London: Oxford University Press. pp. 128–139.
-
21
Using weather variability to estimate the response of savings to transitory income in ThailandAmerican Economic Review 82:15–33.
-
22
Regionally disaggregated social accounting matrices of Nepal, 1986/87, mimeo, Himalayan Institute of Development, Kathmandu, NepalRegionally disaggregated social accounting matrices of Nepal, 1986/87, mimeo, Himalayan Institute of Development, Kathmandu, Nepal.
-
23
Trade liberalization and poverty: The evidence so farJournal of Economic Literature 42:72–115.
Article and author information
Author details
Publication history
- Version of Record published: June 30, 2010 (version 1)
Copyright
© 2010, Cockburn et al.
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

