Economic growth and income distribution: linking macro- economic models with household survey data at the global level

Cite this article as: M. Bussolo, R. E. De Hoyos, D. Medvedev; 2010; Economic growth and income distribution: linking macro- economic models with household survey data at the global level; International Journal of Microsimulation; 3(1); 92-103. doi: 10.34196/ijm.00027

Article
Figures and data
Jump to

Abstract

This paper describes in detail the analytical structure of the Global Income Distribution Dynamics (GIDD) model, a global macro-micro modelling framework, and provides some examples of its recent applications. GIDD is the first macro-micro global simulation model focused on long-term, global growth and distribution dynamics. GIDD has been applied in analyzing the effects of multilateral trade liberalization or mitigation of climate change damages, among others. It also explicitly considers long term time horizons during which changes in the demographic structure are crucial components of both growth and distribution dynamics. The challenges of assessing plausible worldwide distributional implications of growth, large shocks, and policy changes are daunting. Although addressing these issues in a macro-micro framework is subject to great uncertainty, a clearly superior alternative is not yet available.

1. Introduction

The growing availability of micro data sets – such as those from household surveys, labour force surveys, population censuses, and community-level surveys – and progress in quantitative economic analysis have contributed to a renewed academic and policy relevant interest on the mutual relationship between growth and distribution. Macro-micro modelling frameworks that deal with the difficulties of specifying proper macroeconomic counterfactuals while embedding sufficient distributional detail represent one of the most promising emerging methods in empirical analysis. Various types of macro-micro modelling framework have appeared in the recent literature and they have been applied to study different aspects of the growth-distribution-poverty nexus. These range from ex-post studies, such as Robilliard et al. (2008), to ex-ante simulation studies, such as Bourguignon et al. (2002) and Bourguignon and Savard (2008). Comprehensive surveys are also found in Bourguignon and Pereira de Silva (2003), Bourguignon et al. (2008) and Davies (2009).

This paper describes in details the analytical structure of the Global Income Distribution Dynamic (GIDD) model, a global macro-micro modelling framework. It also provides a short description of the different strands of the empirical literature on which this model is based and provides some examples of its recent applications.

While building on past efforts, the GIDD introduces some important new features. First, by including 121 countries and covering 90 per cent of the world population, it is the first macro-micro global simulation model. This extensive coverage allows the GIDD to address questions which would not be tractable with other methods. For example, GIDD can assess growth and distribution effects of global policies such as multilateral trade liberalization or mitigation of climate change damages, among others. The global nature of the modelling framework permits decomposing inequality dynamics into a component due to changes in average income between countries and a component due to widening disparities within countries.

A second important novelty is that is that GIDD explicitly considers long term time horizons during which changes in the demographic structure may become crucial components of both growth and distribution dynamics. The explicit long-term focus of the GIDD can capture the impacts of aging and other demographic changes, such as the skill composition of a population, which may become crucial components of both growth and distribution dynamics.

The paper is organized in the following way. Section 2 presents a detailed description of the model‗s methodology and the mathematical statement, including the re-weighting procedure to capture ex-ante changes in demographic structure and the transmission of counterfactual prices and volumes from the general equilibrium model to the micro data. Section 3 shows three recent applications of the GIDD: (i) the prospects for global income distribution in 2030, (ii) the importance of agricultural trade liberalization for global poverty, and (iii) the distributional impacts of damages from climate change. Finally, concluding remarks can be found in Section 4.

2. Methodology and model approach

Economic development is a complex process associated with changes in demographic composition, urbanization rates, labour market participation, education attainments, and saving rates (Bourguignon et al., 2005). Although no single model is able to capture all these features and their possible interactions, macro-micro simulation models attempt to take into account at least some of the basic mechanisms. This section presents the step-by-step explanation of the methodological approach of the GIDD, which is motivated by the Oaxaca-Blinder decomposition following Bourguignon et al. (2005).

The distribution D of income y at time t can be expressed as the product of the joint distribution of all relevant household or individual characteristics X and the distribution of income conditional on these characteristics:

f_{t} (y) = D_{t} = \int \dots \int_{c (X)} g_{t} (y | X) v_{t} (X) d X

where is the density function of the distribution of income and the summation is over the domain C(X) on which X is defined. Define an income generation model describing household per capita income (Y) as a function of household members’ characteristics or endowments (X), the market reward for those characteristics (β), a set of parameters λ defining labour force participation and occupation status (L|λ), and unobservable components(ε):

Y_{i, t} = f (X_{i, t}, β_{t}, (L_{i, t} | λ_{t}) ε_{i, t})

Household per capita income (or its version accounting for economies of scale) is perhaps the best proxy for household welfare, therefore any economic policy should be assessed in terms of its impact on this indicator. Vector {Y_i,t...Y_N,t} also determines the scalar measures of population welfare such as income distribution and poverty. The income distribution D for a population of N individuals or households at time t can be therefore defined in terms of endowments, prices, labour status and unobservables:

\begin{array}{l} D_{t} & = & {Y_{1, t} \dots Y_{N, t}} \\ = & {f (X_{1, t}, β_{t}, (L_{1, t} | λ_{t}), ε_{1, t}) \dots f (X_{N, t}, β_{t}, (L_{N, t} | λ_{t}), ε_{N, t})} \end{array}

The objective of this paper is to define the counterfactual values of endowments, prices, and labour status. This is certainly not a minor task and becomes even more challenging when done for 73 countries representing 90 percent of the world’s population.¹ To do so, the functional form of Equation (1) has to be defined in a simple fashion using only those independent variables that are available for all countries in the sample. The GIDD’s right hand side variables include age, education endowments and sector of employment of the household head (country subscripts excluded for simplicity):

\begin{matrix} Y_{i, t} = α_{t} + β_{1, t} (D_{i, t}^{A} D_{i, t}^{s}) + β_{2, t} (D_{i, t}^{N A} D_{i, t}^{s}) + β_{3, t} (D_{i, t}^{N A} D_{i, t}^{u s}) \\ + \sum_{k = 1}^{K} γ_{k, t} F_{k, t} + ε_{i, t} \end{matrix}

where D^A and D^NA are dummy variables taking the value of 1 if the household head is employed in the agricultural sector or in the non-agricultural sector, respectively; D^s and D^us are dummy variables identifying skilled and unskilled household heads, respectively. F_k captures the proportion of household members in each of the k age cohorts. The ßs are rewards (prices) to education endowments conditional on the sector of employment and γ^s are prices associated with household composition. Finally ε includes all other income determinants not included in Equation (3). The counterfactual expression to (3) is:

\begin{matrix} {\hat{Y}}_{i, t + 1} = {\hat{α}}_{t + 1} + {\hat{β}}_{1, t + 1} ({\hat{D}}_{i, t + 1}^{A} {\hat{D}}_{i, t + 1}^{s} ({\hat{F}}_{k, t + 1})) + \\ {\hat{β}}_{2, t + 1} ({\hat{D}}_{i, t + 1}^{N A} {\hat{D}}_{i, t + 1}^{s} ({\hat{F}}_{k, t + 1})) + \\ {\hat{β}}_{3, t + 1} ({\hat{D}}_{i, t + 1}^{N A} {\hat{D}}_{i, t + 1}^{u s} ({\hat{F}}_{k, t + 1})) + \\ \sum_{k = 1}^{K} γ_{k, t} {\hat{F}}_{k, t + 1} + ε_{i, t} \end{matrix}

where the demographic characteristics, endowments, and returns to these endowments have been modified in accordance with the counterfactual scenario and the intercept captures the per capita economy-wide growth rate ( $({\hat{α}}_{t} +_{1}) \cdot^{2}$ ).² The counterfactual distribution ${D^{'}}_{t}$ is therefore:

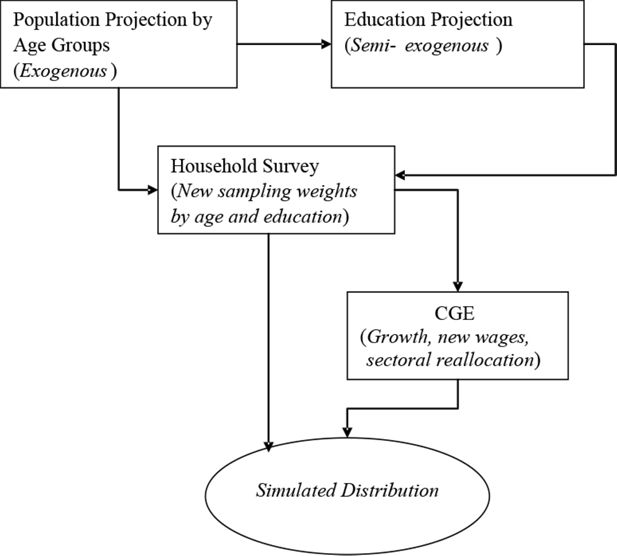
\begin{array}{l} {\hat{D}}_{t} & = & {{\hat{Y}}_{1, t} \dots {\hat{Y}}_{N, t}} \\ = & {f ({\hat{X}}_{1, t}, {\hat{β}}_{t}, ({\hat{L}}_{1, t} | {\hat{λ}}_{t}), ε_{1, t}) \dots f ({\hat{X}}_{N, t}, {\hat{β}}_{t}, ({\hat{L}}_{N, t} | {\hat{λ}}_{t}) ε_{N, t})} \end{array}

In reality, the model parameters change simultaneously; however, for simplicity and tractability, the GIDD modifies each of these sequentially, as shown in Figure 1.

Figure 1

Download asset Open asset

The first step consists of accounting for changes in the size of groups formed by age and education characteristics (top boxes of Figure 1). The impact of these changes on the labour supply is used as an input into a computable general equilibrium (CGE) model (link between the middle and bottom rectangles). In the second step, the CGE model produces a counterfactual scenario for a set of linkage aggregate variables (LAVs), which include overall economic growth, growth in relative incomes by skill (education) and sector, sectoral reallocation of labour, and a new vector of consumer prices. Finally, the changes in the LAVs are passed on to the counterfactual income distribution which has already been adjusted for changes in the age and education structure (bottom link in Figure 1). These steps are described in more detail below.

2.1 Step 1: Socio-Demographic and Educational Changes

The first step in the microsimulation exercise is to implement a set of changes in the demographic structure. We partition the population of each country into m groups of individual-level characteristics targeted by the microsimulation model. In this case, the groups are formed by an intersection of 20 five-year age cohorts and three levels of educational attainment: primary, secondary, and tertiary, although the methodology can incorporate any number of additional partition rules: by gender, geographic area, ethnicity, etc The size of different age groups is modified following the UN medium-variant population projections.³

Micro data shows that for most countries in the world, younger generations tend to be better educated than older ones. It is therefore relatively safe to claim that as the population ages it also becomes better educated, in other words, there is a joint distribution of age and education endowments (Lutz & Goujon, 2001). These two elements, i.e. aging and human capital accumulation conditional on aging, are the first inputs towards the construction of our counterfactual:

F_{k, t + 1} = {\overset{⌢}{F}}_{k, t + 1}

\begin{matrix} D_{i, t + 1}^{s} = {\overset{⌢}{D}}_{i, t + 1}^{s} ({\overset{⌢}{F}}_{k, t + 1}) \\ D_{i, t + 1}^{u s} = {\overset{⌢}{D}}_{i, t + 1}^{u s} ({\overset{⌢}{F}}_{k, t + 1}) \end{matrix}

As the population ages, the average educational attainment in a country increases through a pure “pipeline” effect, as younger and more educated cohorts replace older cohorts (hence the process is referred to as semi-exogenous in Figure 1). For example, if at time t half of the population in the cohort formed by individuals between 25 and 30 years of age have post-secondary education, then after ten years (at t+10), half of the population between 35 and 40 will have post-secondary education. Furthermore, a question remains to be answered: what happens to the younger cohorts of individuals who are still in school? The assumption is that there is no improvement in enrolment and graduation rates from those observed at time t. In other words, the average educational attainment of these young cohorts in the future is equal to the average educational levels of the 20 to 24 cohort of time t. This is a conservative assumption given that the 20 to 24 cohort observed at time t may not have the maximum educational level attainable.

Due to the methodological difficulties in estimating a joint fertility and educational choice model—and the lack of data required to estimate such a model in many household budget surveys—the GIDD uses a non-parametric method to target changes in the demographic structure. A new set of m age-education groups is produced by re-weighting the original surveys, such that each additional member of the population within each partition is an exact replica of the average member of each partition before the reweighting.

Begin with a matrix of individual sampling weights W=[w_mn], where N is the number of observations in the sample and m is a vector of individual-level characteristics targeted by the microsimulation model. Since in the majority of surveys the household, rather than the individual, is the sampling unit, the individual weight is often, but not always, the household weight divided by the number of household members.⁴ The sum of all weights in W gives us total population P: ⁵

P = \sum_{m = 1}^{M} \sum_{n = 1}^{N} w_{m, n}

Summation over n defines the totals of the relevant population sub-groups P_m:

P_{m} = \sum_{n = 1}^{N} w_{m, n} \forall m = 1, \dots, M

Combined with the exogenous population forecasts, the semi-exogenous “pipeline” projections of skill levels (Figure 1) yield the target (or expected) population in each sub-group m such that:

{\hat{P}}_{m} = \sum_{n = 1}^{N} a_{m, n} w_{m, n} \forall m = 1, \dots, M

where A=[a_mn] is a matrix of multipliers which ensure that the m constraints on the future structure of the population are satisfied.⁶ This system has (mxn)-1 variables but only m constraints and is therefore underdetermined. The two possible solutions are to add equations to make the system exactly identified, or to solve an optimization problem that minimizes the distance between the original matrix W and the final matrix (A.W). Both solutions are available in the GIDD.

The first approach imposes the restriction that the multipliers must be equal for each sub-group m:

a_{m, n} = {\bar{a}}_{m} \forall m = 1, \dots, M

This approach reduces the problem to a system of m equations and m unknowns and thus yields an easy solution:

{\bar{a}}_{m} = {\hat{P}}_{m} (\sum_{n = 1}^{N} w_{m, n})^{- 1} \forall m = 1, \dots, M

Beyond its simplicity, there is one additional advantage of this method: it maintains the original distribution of personal characteristics within each of the m population sub-groups. In other words, the distribution of personal characteristics in differs from the distribution in P only due to changes in the between-group variance. Therefore, within the m groups, the original survey design remains unaltered.

Despite these advantages, the above method can produce significantly flawed results if the sampling units are sufficiently dispersed across the m sub-groups. For example, if the variable of interest is household per capita consumption and the m sub-groups span across age and skill endowments, relatively few households would fall entirely into one sub-group. For households spanning more than one sub-group, the re-weig $\overset{⌢}{}$ hting procedure will then assign higher sampling weights to some household members and lower weights to others. This is unsatisfactory for two reasons. First, the intention of any nonparametric re-weighting procedure is to produce “clones” of observations in the initial dataset. However, the structure of an average household in will differ from the structure of the average household in P.

Second, the procedure can also have unintended consequences for the distribution of per capita consumption. Consider two households: one is composed of two “old” individuals, while the other contains one “old” and one “young” member. With an upward-sloping age-consumption profile, the per capita consumption of the first household would generally be above those of the second. As the population ages, the first household will become more representative of the overall demographic structure and the average consumption in the population will increase. However, in the procedure described by Equation (5), the increase in consumption due to higher weight of the first household will be somewhat offset by the rising contribution of the second household which has lower per capita consumption (because both the sampling weights are increased for both households). Therefore, the upward-sloping age-consumption profile observed in the cross-section may not be accurately reflected in the outcome of the re-weighting procedure.

In order to address these shortcomings, the GIDD can also estimate the A matrix by minimizing a distance function, similar to the methodology of Robilliard and Robinson (2003) and Cai et al., (2006). However, it differs from the previous efforts in one crucial aspect by explicitly recognizing the importance of maintaining the household structure of the original survey. Consider minimizing the following objective function:

\sum_{n} 0.5 {(\frac{\sum_{m = 1}^{M} a_{m, n} w_{m, n}}{\sum_{m = 1}^{M} w_{m, n}} - 1)}^{2}

subject to the constraints in Equation (6) and an additional set of constraints below:

r_{m, n} = \frac{w_{m, n}}{\sum_{m = 1}^{M} w_{m, n}} = \frac{a_{m, n} w_{m, n}}{\sum_{m = 1}^{M} a_{m, n} w_{m, n}}

The solution to this minimization problem is a matrix A that penalizes the squared percentage deviations of (A.W) from W while meeting the set of sub-group constraints and keeping the original ratio of individual to household weights unchanged for each household in the sample (Equation 3.10). Equation (10) implies that:

a_{m, n} = {\bar{a}}_{n} \forall n = 1, \dots, N

which allows for a convenient re-statement of the minimization problem by simplifying Equation (9) and combining Equations (6) and (11):

\min \sum_{n} 0.5 {({\bar{a}}_{n} - 1)}^{2}

subject to

{\hat{P}}_{m} = \sum_{n = 1}^{N} a_{m, n} w_{m, n} = \sum_{n = 1}^{N} {\bar{a}}_{n} w_{m, n}

The solution to this minimization problem (detailed in Appendix 1) is:

{\bar{a}}_{n} = 1 + \sum_{m = 1}^{M} \frac{{\hat{P}}_{m} - P_{m}}{\sum_{j = 1}^{N} w_{m, j} w_{j, m}} w_{m, n}

which gives us the a_i,t parameters discussed in the introduction to this section and therefore completes the first step of the microsimulation.

2.2 Step 2: Macroeconomic Changes

The socio-demographic changes captured by the above procedure are likely to have important consequences for economic growth and the distribution of income within a given country. For example, population aging is generally correlated with declining saving rates and changing demand patterns, while rising average skill endowments could reduce the observed skill wage premiums. In an increasingly globalizing world, the direction and magnitude of these changes will also be affected by the changing patterns of international flows of goods, services, and capital. In order to capture all of these effects in a consistent fashion, the GIDD is linked to a global computable general equilibrium (CGE) model to obtain a set of counterfactual prices (factor returns) and quantities (factor volumes); these are essentially the link aggregate variables (LAVs) of Ferreira et al. (2003). Currently, the CGE model used with the GIDD is the World Bank’s global LINKAGE model, although the microsimulation methodology is compatible with any CGE model that has sufficient factor market detail.

LINKAGE is a relatively standard CGE model with many neoclassical features (for the full model description, see van der Mensbrugghe 2006). It is currently based on the Global Trade Analysis Project (GTAP) Release 6.3 dataset with a 2001 base year.⁷ The model is solved in a recursive-dynamic mode in which a series of end-of-period equilibriums are linked with a set of equations that update the main macro variables. The three particularly relevant aspects of LINKAGE (for the purposes of the GIDD) are its multi-sectoral nature and its detailed treatment of factor markets and international trade and capital flows.

The inclusion of multiple productive activities and multiple commodities allow for a rich production and demand structure. Productivity trends are sector- and factor-specific, and are calibrated to be consistent with historical evidence as well as World Bank’s near- and medium-term GDP growth forecasts. The allocation of household budget (for a single representative household in each country) across saving and a vector of consumption commodities is determined simultaneously through maximization of an extended linear expenditure system (ELES). The system captures various substitution possibilities across commodities as well as a gradual shift in demand towards commodities with higher income elasticities (e.g., manufacturing and services) over time.

Production is modeled in a nested constant elasticity of substitution (CES) fashion to reflect various substitution possibilities across inputs (see Figure 2). This allows for a rich treatment of factor markets, where returns to factors of production—unskilled and skilled labour, capital, land, and natural resources—can be type- and sector-specific. In standard GIDD applications, capital and well as skilled labour are perfectly mobile across sectors within a country, while the market for unskilled labour is segmented into farm- and non-farm categories. Within each segment, labour is perfectly mobile across activities, but mobility across segments is limited by a migration function which responds to changes in the farm- and non-farm wage premiums. The LINKAGE model also allows for international mobility of labour and capital as well as changes in the unemployment rate, but none of these possibilities are currently modelled within the GIDD.

Figure 2

Download asset Open asset

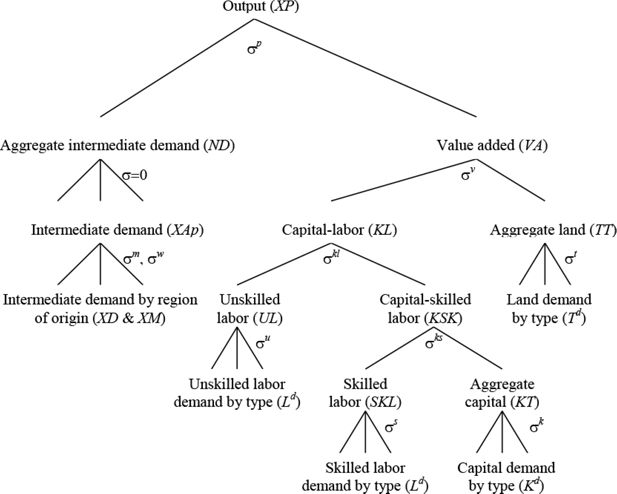
Nested structure of production in LINKAGE.

*Source*: van der Mensbrugghe (2006: 62).

International trade is modelled using the nested Armington specification, in which consumer products are differentiated by region of origin and combined using CES functions.⁸ On the supply side, producers allocate output to domestic and export markets according to a constant elasticity of transformation (CET) specification. The global nature of the model means that all countries have some degree of market power, goods and services markets clear at the international level, and global capital flows are balanced. The degree of international openness—both trade and capital—affects domestic factor prices directly but also has important consequences for the growth of factor productivity.

2.3 Step 3: Labour Reallocation

Changes in the rate of exit of workers from the traditional agricultural sector into manufacturing and services may occur as an outcome of the baseline growth process or as a result of specific policy interventions that affect the wage gap between the two types of activities. Workers will choose to abandon the agricultural sector if this choice represents an increase in their expected earnings. Therefore, any change in the rate of re-allocation of labour across sectors will have an impact on income distribution. At the macro level, the CGE model will predict the number of workers moving out of the traditional agricultural sector into the relatively modern industrial and service sectors. At the micro level, the macro constraint of moving N workers out of agriculture and into manufacturing and service activities can be satisfied by a large number of potential combinations of workers.

Some studies resolve this ambiguity by randomly picking migrants from the agricultural labour supply until the aggregate constraint is satisfied. The GIDD employs a more sophisticated methodology by estimating a set of parameters of the conditional probability function of being a worker in the non-agricultural sector, ranking the workers in the agricultural sector according to their probability score, and assigning migrant status to workers with the highest score until N workers have been selected. Currently, this procedure is implemented at the household level—where the head of household makes the migration decision and takes the rest of the household members with her—although the methodology can also be applied at the individual level.⁹

The probability of observing that individual j works in the non-agricultural sector is modelled with a probit equation:

\Pr (N A_{j} = 1) = P (X_{j}, Z_{j})

where X_j and Z_j and are vectors of personal and household characteristics of individual j, respectively. Following estimation, workers in the agricultural sector are assigned a probability score based on their X and Z characteristics and the estimated vector of common determinants ${λ^{'}}_{t} \cdot$ . The workers are then ordered based on this probability score, and workers with higher probabilities to be in non-agricultural sectors are moved out of the agricultural sector up to a point where the predicted share of workers by sector (the macro constraint) is satisfied.

Once the agricultural workers with a highest likelihood of being in non-agricultural sectors have changed sector of employment, the next step is to adjust their labour remuneration. The first step in this process is estimating a Mincer equation for workers in agricultural (A) and non-agricultural (NA) sectors:

In(Y)_{j, s} = X_{j} β_{s} + ε_{j, s} where s = (A, N A)

Migrants carry their personal endowments X_j and their residual ε_j from one sector to the other. Nevertheless once they arrive to the non-agricultural sectors, their vector of personal characteristics X_j will be rewarded with prices ß_NA and their residuals will be re-scaled to take into account the differences in the distribution of unobservables between the agricultural and non-agricultural sectors. Hence assuming worker j is a migrant her income assignment function will be defined as:

In {(Y)}_{j, N A} = X_{j} β_{N A} + ε_{J}^{*}

where

ε_{j}^{*} = ε_{j, A} \frac{σ_{ε, N A}}{σ_{ε, A}}

and σ_ε,S is the standard deviation of the distribution of residuals in sector s.

2.4. Step 4: Income Assignment

The final step in the GIDD microsimulation is to adjust factor returns by skill and sector, as well as the average income/consumption per capita, in accordance with the results of the CGE model. Because the individual and/or household income generating process is modelled structurally in the macro model but can only be estimated in its reduced form in the micro model, the GIDD does not modify each of the components of the ß_t vector, as is customarily done in decomposition or microsimulation exercises relying exclusively on micro data (see Bourguignon et al., 2005). Instead, the GIDD imposes an entirely new vector of earnings ß^’_s,e,t on each worker, conditional on that worker being in sector s and having an educational attainment e. The imposition of the ${β^{'}}_{t}$ vector completes the microsimulation, save for a final within-country rank-preserving normalization to guarantee that each country’s per capita income/consumption changes exactly in line with the CGE results.

There are two potential difficulties in translating the price changes of the CGE model into the micro data. First, following the implementation of the re-weighting and migration routines certain changes have already taken place both in the average survey income and its distribution. Therefore, the macro constraints on changing returns to sector and skills [y_s,l] as well as the average income $\bar{y}$ are imposed net of the changes that have already taken place up to this stage. Second, achieving full consistency between macro and micro data is often difficult if not impossible.¹⁰ Since there is no guarantee that the first period wages in the CGE model match the labour earnings in the micro data, directly passing the changes in factor returns from the former to the latter may result in inconsistent evolution of wage premiums in the two models. In extreme cases, wage gaps may even be reversed in one model but not in the other. In order to hedge against these potential complications while ensuring maximum consistency between the macro and micro outcomes, the GIDD adjusts the ratios between wage premiums rather than wages themselves.

Beginning with a distribution of earnings by sector and skill [y_s,l] in the macro data, define a series of (s+/-1)wage gaps as follows:

g_{s, l} = \frac{y_{s, l}}{y_{1, 1}} - 1

where y_1,1 is the average labour earnings of unskilled workers in agriculture. The micro data will have a set of wage premiums $[{g^{'}}_{s, l}]$ which may or may not be consistent with the macro data. The counterfactual wage gaps in the GIDD will then be calculated as:

{\hat{g}}^{'}_{s, l} = {g^{'}}_{s, l} \frac{{\hat{g}}_{s, l}}{g_{s, 1}}

This implies that even if initial and final wages differ between the macro and micro models, the percentage change in the wage gaps (themselves expressed as percentage premiums over labour earnings of unskilled workers in agriculture) will be consistent across the two models. This eliminates the possibility of wage gap reversal and ensures that the distributional changes are consistently mapped from the macro to the micro data.

Note that Equation (16) does not change the average earnings of unskilled workers in agriculture and only operates on labour income. In order to adjust the micro data such that the percentage change in the per capita income/consumption Y′ matches the change in real consumption per capita Y in the CGE model, a final normalization adjustment is carried out:

\overset{⌢}{Y^{'}} = Y^{'} \frac{\overset{⌢}{Y}}{Y}

The rank-preserving transformation of Equation (17) implicitly accounts for changes in land, natural resource, and capital prices because these enter the household budget constraint in the CGE model and thus have an income effect on consumption. Therefore, the income adjustment process described in Equations (15) and (17) allows the changes in labour remuneration to affect the income distribution of a given country, but the change in welfare at the national level is determined by the changes in all factor prices, including land and capital.

This approach conveniently avoids the issue of identifying sources of household income different from labour, but is justifiable on several grounds. First, it avoids the difficulties involved in estimating the contribution of capital to household earnings.¹¹ Second, movements in skilled wage and returns to capital are often correlated, so the GIDD is able to capture the distributional impacts of changing returns to capital through Equation (16). Third, the empirical literature on decomposing changes in the income distribution over time (e.g. Bourguignon et al., 2005) is usually able to explain much of the change in total inequality without resorting to estimation of capital incomes.

3. Applications

The GIDD framework has been used in various studies. To provide some examples of findings that can be generated from a GIDD-based analysis, this section briefly summarizes the results from three recent applications. The first considers potential trends in the global income distribution over the next couple of decades, the second application highlights the likely distributional impacts of liberalization of trade in agriculture, and the third addresses the changes in global income distribution and global poverty due to damages from climate change.

3.1 Global income distribution in 2030

In the first application the GIDD in conjunction with a global computable general equilibrium model is used to generate a new income distribution for the year 2030 (see Bussolo et al., 2009). No major policy changes are introduced, and the growth assumptions are based on productivity trends from the past two decades and the short- and medium-term country-specific forecasts by the World Bank. This study then identifies the drivers of the expected distributional changes by means of two complementary approaches. The analysis is initially conducted in terms of the convergence and dispersion components, i.e. changes in income disparities between and within countries. Results show that the reduction in global income inequality between 2000 and 2030 is the outcome of two opposing forces: the inequality-reducing convergence effect and the inequality-enhancing dispersion effect (Table 1).

Table 1

Global Income Inequality.

Index	2000	2030	Dispersion Only	Conver-gence Only
Gini	0.672	0.626	0.673	0.625
Theil	0.905	0.749	0.904	0.749
Mean Log Deviation	0.884	0.764	0.893	0.759

Source: Authors’ own calculations using data from GIDD.

Three main findings emerge: first, even with significant changes of within-country inequality levels, all the potential reduction of global inequality can be accounted for by the projected convergence in growth rates of average incomes across countries. Second, the aggregate impact of the changes of the within-countries component of inequality appears to be minor; however specific countries, and specific households’ types within countries, may experience large distributional shifts. Third, a main cause of local inequality changes is the adjustments of factor rewards.

To translate these results into a more practical and policy relevant perspective, this study considers what happens to a specific income group during the 2000–2030 time period. The group under consideration is labelled “global middle class” (GMC) and comprises people whose income levels are between the average incomes of Brazil and Italy, in purchasing power parity terms.¹² The combination of the convergence and divergence components described earlier drive a dramatic increase in the size of the global middle class and its profound compositional change in favuor of developing country nationals. A key conclusion asserts that developing country members of the global middle class are likely to become an increasingly important group within their own countries, will increase their political influence and possibly provide continued momentum for policies favouring global integration.

3.2 Free Trade in agriculture and global poverty

The second GIDD application considers the global poverty and inequality impacts of the full removal of trade taxes and subsidies on all agricultural goods around the world. Almost 45 percent of the population in the world lives in households where agricultural activities represent the main occupation of the head, and a large share of this agriculture-dependent group, close to 32 percent, is poor. Agriculture households contribute disproportionably to global poverty: three out of every four poor people belong to this group (see Table 2). Given global variations in: (a) the importance of the agricultural sector, (b) the agriculture to non-agriculture income premia, (c) the within-sector income inequality, and (d) the initial level and structure of domestic agricultural trade barriers, the resource reallocation following trade reform will have significant distributional effects between and within countries.

Table 2

Poverty is higher among agricultural households even if their incomes are less unequal.

	Gini (%)	Population Share (%)	Average Monthly Income (2000, US PPP)	1-Dollar Poverty Incidence (%)	Poverty Share (%)
Agriculture	44.9	44.8	65.4	31.7	75.9
Non-Agricultural	62.8	55.2	328.9	8.1	24.0
World	67.0	1	210.8	18.7	1

Source: GIDD database.

Three main messages emerge from a comparative static exercise of comparing a world with and without agricultural distortions (see Bussolo, De Hoyos, & Medvedev, 2010). First, the liberalization of agriculture and food markets is unlikely to have large effects on global poverty. It could increase global extreme poverty (US$1 a day) by 0.2 percent and lower moderate poverty (US$2 a day) by 0.3 percent. Second, these small aggregate changes are produced by a combination of offsetting trends at the regional and country levels. Most countries witness a substantial reduction in poverty while South Asia—where half of the world’s poor reside—experiences an increase in extreme poverty incidence due to removal of high initial rates of protection afforded to unskilled-intensive agricultural sectors. Finally, the distributional changes are likely to be mild, but exhibit a strong regional pattern. Inequality is likely to fall in regions such as Latin America, which are characterized by high initial inequality, and rise in regions like South Asia, characterized by low initial inequality.

3.3 Distributional impacts of climate change

In the third application the GIDD is used to study the income distribution and poverty consequences of damages from global warming (see Bussolo et al., 2008). The general equilibrium model with an integrated climate module and links from emissions to global temperature is solved through 2050, and climate change damages to agricultural productivity are calibrated using estimates in Cline (2007). In order to assess the magnitude and incidence of climate change damages, the baseline scenario (which incorporates climate feedbacks to agricultural productivity) is contrasted with an alternative scenario where the damage coefficient is set to zero (i.e., costless mitigation). The results show that a temperature increase of approximately 1 degree C above today’s levels could raise the 2050 global moderate poverty headcount (2 dollars per day poverty line) from 2.85 percent in a scenario with no damages to 3.01 percent when damages are taken into account. The limited global impact conceals a wider variation across regions, with increases in poverty ranging from 289 thousand people in Latin America and the Caribbean to 2.7 million in South Asia and 6.2 million in Sub-Saharan Africa.

The adverse effects of global warming also vary by the main source of household earnings. Although climate change damages are concentrated in agriculture, the agricultural households are not necessarily the most affected.

Due to a reduction in global output of agriculture of 1.5 percent (and nearly 12 percent in developing countries), prices for agricultural products rise and help close the wage gap between earnings in the farm and non-farm sectors. At the same time, however, the cost of the food basket rises for all consumers, including agricultural households. As a result, households in the farm sector are still likely to experience a reduction in their welfare due to higher consumption costs and the slower rate of growth in global GDP, but this reduction is likely to be less pronounced than the welfare losses for non-farm households. At the global level, these trends translate into a 0.2 percentage point increase in the non-farm poverty headcount while the headcount in agriculture rises by just 0.1 percentage points.

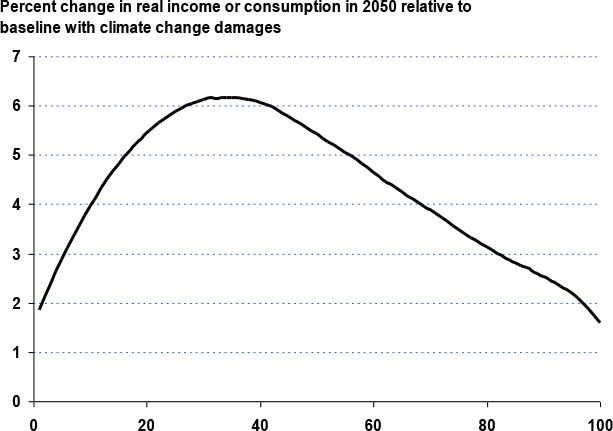
Because the adverse impacts of global warming are more pronounced in the poor countries located closer to the equator, including climate change damages in the analysis results in an increase in the global Gini coefficient from 57.2 to 57.6 in 2050. The widening of inequality between countries is somewhat offset by the falling within component due to faster growth in the earnings of agricultural households, which tend to be concentrated in the left tail of the national distributions. These dynamics give rise to the global growth incidence curve in Figure 3, which shows the distribution of per capita income gains if climate change damages were zero. Because these gains are largest between the 2nd and 6th decile of the global income distribution, households in this part of the distribution are likely to suffer the most from climate change (i.e., they have the most to gain if climate change had zero impact on agricultural productivity).

Figure 3

Download asset Open asset

Global incidence of climate change damages.

*Source*: Simulations with World Bank’s GIDD model.

4. Conclusions

In an increasingly globalized world, many domestic policies have an impact that goes beyond the country’s own frontiers; similarly, several economic policy proposals have a global nature, e.g. trade liberalization agendas, policies mitigating climate change, etc. The GIDD is able to incorporate, in an ex-ante fashion, changes in demographic composition, sectoral re-allocation of labour, shifts in relative wages and overall growth and it thus represents an important step towards a more integrated global macro-micro evaluation framework. This paper develops the methodology in detail and then illustrates its usefulness by showing three recent applications of the GIDD: (a) potential evolution of the global income distribution through 2030, (b) distributional and poverty impacts of removing distortions to trade in agriculture, and (c) the incidence of damages from global warming over the next 40 years. Although the GIDD represents an important contribution to our understanding of the global welfare effects of macro policies, more research is needed to update the GIDD’s data and expand its modelling capabilities.

Footnotes

1.

For a full list of countries included in the GIDD see www.worldbank.org/prospects/gidd.

2.

The intercept in fact captures the residual average rate of growth, after all other changes—demographic, endowments, and prices—have already been taken into account.

3.

The assumptions behind these projections can be found in: http://esa.un.org/unpp/

4.

Certain surveys (e.g., Brazil and Venezuela) target certain individual-level characteristics (such as the gender composition of the sample) and therefore adjust the sampling weights at the individual level to be consistent with the census data.

5.

In most cases, aggregate statistics like census data will differ from the sum of micro sources such as household surveys; a cross-entropy method to reconcile household survey and national accounts data is developed in Robilliard and Robinson (2003).

6.

In matrix terms, this can be expressed as $\hat{p}$ =(A.W)i_n where (A.W) is the hadamard product and i_n is an identity column vector. Note that we are not imposing the total population constraint

P = \sum_{m = 1}^{M} \sum_{n = 1}^{N} a_{m, n} w_{m, n} = (A . W) i_{n} i'_{m}

which make the system over-determined in m variables. The underlying assumption is that the sub-group targets ${\hat{p}}_{m}$ _m add up to the total population $\hat{p}$ (either originally or following normalization by the user), which makes one of the equations linearly dependent of the others and allows us to drop it.

7.

The Global Trade Analysis Project (GTAP) database and model are disseminated by Center for Global Trade Analysis of Purdue University. See http://www.gtap.org and Hertel (1999).

8.

See Armington (1969).

9.

The choice for implementing the migration routine at the household level is driven by data constraints. In a large number of GIDD surveys (particularly consumption-based surveys, which make up 54 of the 73 surveys in the GIDD) contributions of individual incomes to total household income cannot be identified, forcing us to operate at the household level.

10.

See the discussion in Bourguignon, Bussolo and Pereira de Silva (2008) for a more detailed statement of this consistency problem and some examples.

11.

Most econometric solutions to the problem of imputing capital earnings ignore the selection bias in the self-employment decision. Furthermore, it is questionable whether it is possible even in principle to extract information on capital income from surveys that are generally not designed to capture this information and where definitions of “capital” may vary widely between micro data and national accounts.

12.

In 1993 PPP prices, the lower threshold is 303 dollars per person per month, while the upper threshold is 611 dollars per person per month. This means that per capita earnings of members of the global middle class are 10 to 20 times above the international poverty line of 1 dollar a day. These income thresholds are due to the global middle class definition proposed by Milanovic and Yitzhaki (2002).

Solution to the minimization problem

Define the minimization problem as follows:

\min \sum_{n} 0.5 {({\bar{a}}_{n} - 1)}^{2} s.t.

{\hat{P}}_{m} = \sum_{n = 1}^{N} a_{m, n} w_{m, n} = \sum_{n = 1}^{N} {\bar{a}}_{n} w_{m, n}

The first order conditions are:

{\bar{a}}_{n} = 1 + \sum_{m = 1}^{M} λ_{m} w_{m, n}

{\hat{P}}_{m} = \sum_{n = 1}^{N} {\bar{a}}_{n} w_{m, n}

These can be written in matrix form as follows:

[\begin{matrix} I & - W^{'} \\ W & 0 \end{matrix}] [\begin{matrix} A \\ Λ \end{matrix}] = [\begin{matrix} i_{n} \\ \hat{P} \end{matrix}]

The solution is:

[\begin{matrix} A \\ Λ \end{matrix}] = [\begin{matrix} 0 & W^{'} {(W W^{'})}^{- 1} \\ - {(W W^{'})}^{- 1} W & {(W W^{'})}^{- 1} \end{matrix}] [\begin{matrix} i_{n} \\ \hat{P} \end{matrix}]

which gives a simple expression for Λ:

Λ = {(W W^{'})}^{- 1} (\hat{P} - W i_{n})

The matrix to invert is mxm, which considerably reduces the dimensionality of the problem. Once the values for Λ are known, the first order condition can be used to obtain a solution for the A matrix.

References

1
A Theory of Demand for Products Distinguished by Place of Production
1. P Armington
(1969)
International Monetary Fund Staff Papers, 16.
- Google Scholar
2
The poverty-growth-inequality triangle
1. F Bourguignon
(2004)
paper presented at the Indian Council for Research on International Economic Relations.
- Google Scholar
3
The Impact of Economic Policies on Poverty and Income Distribution: Evaluation Techniques and Tools
1. F Bourguignon
2. L Pereira da Silva
(editors) (2003)
Oxford: World Bank and Oxford University Press.
- Google Scholar
4
Distributional effects of trade reform: an integrated macro-micro model applied to the Philippines
1. F Bourguignon
2. L Savard
(2008)
In: F Bourguignon, M Bussolo, LA Pereira Da Silva, editors. The Impact of Macroeconomic Policies on Poverty and Income Distribution. Washington, DC: The World Bank. pp. 177–213.
- Google Scholar
5
World Bank Policy Research Working Paper
(2002)
World Bank Policy Research Working Paper, 2828, World Bank, Washington DC.
- Google Scholar
6
The Microeconomics of Income Distribution Dynamics in East Asia and Latin America
(editors) (2005)
Oxford: Oxford University Press.
- Google Scholar
7
The Impact of Macroeconomic Policies on Poverty and Income Distribution - Macro-Micro Evaluation Techniques and Tools
(editors) (2008)
Washington DC: The World Bank and Palgrave Macmillan.
- Google Scholar
8
Global Climate Change and its Distributional Impacts
(2008)
Global Climate Change and its Distributional Impacts, mimeo, The World Bank, Washington, D.C..
- Google Scholar
9
The Future of Global Income Inequality
(2009)
In: A Estache, D Leipziger, editors. Stuck in the Middle. Washington D.C.: Brookings Institution Press. pp. 54–75.
- Google Scholar
10
Global Poverty and Distributional Impacts: The GIDD Model
(2010)
In: K Anderson, J Cockburn, W Martin, editors. Agricultural Price Distortions, Inequality, and Poverty. Washington D.C.: The World Bank. pp. 87–119.
- Google Scholar
11
Accounting for population ageing in tax microsimulation modelling by survey reweighting
1. L Cai
2. J Creedy
3. G Kalb
(2006)
Australian Economic Papers 45:18–37.
- Google Scholar
12
Global Warming and Agriculture: Impact Estimates by Country
1. W R Cline
(2007)
Center for Global D velopment and Peterson Institute for International Economics, Washington, DC.
- Google Scholar
13
Combining microsimulation with CGE and macro modelling for distributional analysis in developing and transition countries
1. J Davies
(2009)
The International Journal of Microsimulation 2:49–65.
- Google Scholar
14
Global poverty and inequality: a review of the evidence. World Bank Policy Research Working Paper, 4623
1. FHG Ferreira
2. M Ravallion
(2003)
Washington D.C.: World Bank.
- Google Scholar
15
Global Trade Analysis: Modeling and Applications
1. T W Hertel
(1999)
New York: Cambridge University Press.
- Google Scholar
16
The World’s Changing Human Capital Stock: Multi-State Population Projections by Educational Attainment
1. W Lutz
2. A Goujon
(2001)
Population and Development Review 27:323–339.
- Google Scholar
17
Decomposing World Income Distribution: Does the World Have a Middle Class?
1. B Milanovic
2. S Yitzhaki
(2002)
Review of Income and Wealth 48:155–78.
- Google Scholar
18
Reconciling Household Surveys and National Accounts Data Using a Cross Entropy Estimation Method
1. A S Robilliard
2. S Robinson
(2003)
Review of Income and Wealth 49:395–406.
- Google Scholar
19
Examining the Social Impact of the Indonesian Financial Crisis Using a Macro-Micro Model
(2008)
In: F Bourguignon, M Bussolo, LA Pereira Da Silva, editors. The Impact of Macroeconomic Policies on Poverty and Income Distribution. Washington, DC: The World Bank. pp. 93–118.
- Google Scholar
20
The LINKAGE Model Technical Documentation
1. D van der Mensbrugghe
(2006)
Washington, DC: World Bank.
- Google Scholar

Article and author information

Author details

Maurizio Bussolo

Latin America and Caribbean Economic Policy, The World Bank, United States

For correspondence
mbussolo@worldbank.org
Rafael E. De Hoyos

Subsecretaría de Educación Media Superior, D.F.

For correspondence
rdehoyos@sems.gob.mx
Denis Medvedev

Latin America and Caribbean Economic Policy, The World Bank, United States

For correspondence
dmedvedev@worldbank.org

Acknowledgements

The authors are grateful to Francisco Ferreira, Hans Timmer, Dominique van der Mensbrugghe, conference participants at the 2008 International Association for Research in Income and Wealth (IARIW) conference, two anonymous referees, and the editors for helpful discussions, comments, and suggestions. All remaining errors are our own.

The research for this paper has been partially funded by the Hewlett Foundation’s Trust Fund Program: Fertility, Reproductive Health, and Socioeconomic Outcomes. The findings, interpretations, and conclusions expressed in this paper are entirely those of the authors; they do not necessarily reflect the views of the World Bank, its Executive Directors, or the countries they represent.

Publication history

Version of Record published: June 30, 2010 (version 1)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Download citations (links to download the citations from this article in formats compatible with various reference manager tools)

BibTeX
RIS

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

GIDD methodological framework.

Nested structure of production in LINKAGE.

Global Income Inequality.

Poverty is higher among agricultural households even if their incomes are less unequal.

Global incidence of climate change damages.

Author details

Maurizio Bussolo

For correspondence

Rafael E. De Hoyos

For correspondence

Denis Medvedev

For correspondence

Downloads (link to download the article as PDF)

Download citations (links to download the citations from this article in formats compatible with various reference manager tools)

Open citations (links to open the citations from this article in various online reference manager services)

Categories and tags