Modelling household spending using a random assignment scheme
Abstract
Applied demand analysis is usually done by specifying some kind of econometric equation but there are some difficulties associated with this approach. These include the problem of modelling at a highly disaggregated level and the amount of data needed to estimate the parameters for the equations.
This paper examines the use of what are known as random assignment schemes as a way to model household expenditure. This approach is based on the idea of predicting the behavioural response of a microsimulation unit by finding a donor, which is in some sense similar to the receiving unit.
The paper begins with a brief review of econometric modelling. It then introduces the principles of random assignment schemes. These are expanded upon in an illustrative example to model the effect of changes in the level of income on household expenditure patterns. The model is then used as a platform to show how the random assignment scheme can be used to model a large number of goods, at the level of individual households.
1. Introduction
Consumer spending in the UK amounted to 872 billion pounds in 2009 (ONS, 2010). It is understandable therefore, that both commercial and public organisations have an interest in gaining a better understanding of this sector of the economy. In the private sector, this might be to predict the size of the market for particular goods or services. For governments, it is important to understand the effect of indirect taxes that affect households differently depending on the type and quantity of goods they consume. The problem this paper addresses is how to model the way spending on various goods and services varies in response to demographic, economic and socio-technical change.
In microsimulation, as well as in economics generally, modelling household expenditure is usually carried out by econometric methods. However, there are some difficulties with this approach such as the amount of data needed to estimate the parameters accurately (Thomas, 1987) and the difficulty of modelling at a highly disaggregated level (discussed below). This paper examines the use of what are known as random assignment schemes as a way to model household expenditure. This approach is based on the idea of predicting the behavioural response of a microsimulation unit by finding a donor, which is in some sense similar to the receiving unit. According to Klevmarken (1997), the advantages of this method are that it is not necessary to impose a functional form on the data or make any assumptions about the distribution of variables. There are no parameters to estimate and the method preserves the variation and most of the correlation present in the original dataset. The approach also allows the study of situations where people behave in fundamentally different ways; in particular where some individuals do something other than maximise their utility function.
Following a brief review of econometric modelling, the paper introduces the principles of random assignment schemes. These are explicated further in an example model to predict the effect of changes in the level of income on household expenditure patterns. The results are validated by showing that the model reproduces some stylised facts that are already known about household expenditure patterns. The model is then used as a platform to show how the random assignment scheme can be used to model a large number of goods, at the level of individual households.
2. Econometric modelling
In economics, the standard approach to modelling household demand is by using econometric methods. It is possible to do this in a single, regression type equation of the form.
Here, the dependent variable Y might represent the budget share for food. The independent variables X1 to Xn could represent factors that are thought to influence spending on food such as household size, income and price. The constants b0 to bn would be estimated using standard statistical software on observed data that captures the relationship between the relevant variables.
One of the problems with this approach is that it is necessary to specify a separate equation for each good of interest. This becomes unwieldy if the number of goods is large as it would be in a typical household budget set. It is also difficult to model the interaction between spending on each good because, in principle, this will depend on what is spent on all the other goods. The list of independent variables should then include the budget shares of all these items. This is feasible for a small number of goods but as the size of the budget set increases, the number of parameters needed to estimate the model grows quickly to the point where, for most datasets, there are not enough cases to provide accurate estimates of the parameters.
This problem is alleviated to some extent by the use of complete demand systems consisting of an integrated set of equations. One of the most sophisticated is the Almost Ideal Demand System (AIDS, Deaton and Muellbauer, 1980). It uses the principles of neoclassical economic theory to impose restrictions on the possible values of the parameters and so reduce the amount of data needed to estimate them. The AIDS model is used here as a representative of the econometric approach, partly because it may be the most advanced (Alpay & Koc, 1998) and because it seems to be one of the most widely used.
The general model for the Almost Ideal Demand System, for a budget set of i goods is:
where
wi is the budget share of the ith good
M is the total consumption expenditure
Pj is the price of the jth good (j is a good other than i)
P is a price aggregator for the set of goods
εi is an error term for good i
It is possible to take the demographic characteristics of each household into account by including a vector of dummy variables Z.
The dummy variables indicate the presence or absence of the characteristic of interest. Income, for example, could be divided into a number of bands and each household would have a 1 if it is in a particular band and a 0 otherwise. In this way, there is a separate equation, with its own parameters, for each income band.
It can be seen from the γij and the δiz that the number of parameters to estimate increases with the square of the number of goods and as the product of the number of household categories and goods. As a result, this approach is limited to consideration of a relatively small number of goods and household types. It becomes more difficult to apply if the households are to be represented at a highly disaggregated level as they are in microsimulation modelling. Here, as the number of dummy variables increases, the number of parameters becomes prohibitive due to data limitations. Also, the number of income bands is limited by the number of equations in the system so it would not be possible to use continuous variables.
3. Random assignment scheme
The difficulties associated with parametric estimation of demand systems raises the question of whether there are alternative methods that do not involve parameters. Random assignment provides the basis for one such method. The idea of random assignment is usually associated with selecting individuals for treatment groups in such a way that the effect of the treatment is the only source of difference in outcomes between the groups. However, in the context of microsimulation modelling, random assignment is a kind of matching or imputation technique where a donor is selected on the basis of its similarity or closeness to the receiving unit. Klevmarken (1997) provides an example of how a random assignment scheme can be used as a method of projecting a variable over time. Data is available on a set of incomes for two consecutive years along with some related variables such as age and sex. It is desired to project the income distribution for the following year. This is done by first defining a distance metric between a donor’s variables in year 1 and a receiver’s variables in year 2. The essence of the procedure is that the income for each case in year 3 is obtained by finding a donor, whose characteristics in year 1, are similar to those of the current case in year 2. The receiver’s income in year 3 is then assigned to be what the donor’s income subsequently became in year 2.
Random assignment has been used by (Klevmarken et al., 1992) and (Klevmarken & Olovsson, 1996) and more recently by (Holm, Mäkilä, & Lundevaller, 2009) in a dynamic spatial microsimulation model of geographic mobility. They found that this approach had the potential to provide better population projections than the alternative interaction based models. However, they also noted that the representation of behaviour is limited to what has already been observed in the initial data set. This is not a problem when it is desired only to project, all other things being equal, from current data but it is a limitation when applying the method in new situations because the behaviour and correlation structure are locked in to what has been observed. However, the issue of how to extrapolate from observed data is common to all approaches. In microsimulation, this is often done by applying some kind of alignment procedure. It would also be possible to use theoretical assumptions or empirical data to extend the model.
The next part of this paper introduces a simple example application of random assignment to model the effect of changes in household income on household expenditure patterns. This shows the operation of random assignment in more detail.
4. The effect of changes in household income on expenditure patterns
Economic modelling is often carried out at the individual level. This makes sense because it is the individual who makes decisions and has some agency regarding their consumption behaviour. However, it is possible for individuals to have no income of their own yet spend money on a range of items. This is explainable by intra-household allocation of resources and at the individual level, this would have to be represented in the model. Working at the household level encapsulates intra-household allocations implicitly in observed spending patterns and so simplifies the specification of the model.
4.1 Stylised facts
The relationship between household income and spending is an area that has been studied quite extensively. The model described in this section is not intended, primarily, to add to the voluminous literature on this subject. Rather, a few stylised facts are abstracted from what is known and these are used to test the validity and plausibility of the results produced by the model. The main purpose of the model itself is to provide an illustrative example of the implementation of a random assignment scheme and how it operates in practice.
One of the most obvious features of household spending patterns is that total consumption increases with income. However, as incomes rise, not all of it goes to consumption expenditure; some is saved or invested and some is paid in income tax. This means that, as household incomes rise, total expenditure will increase at a slower rate than income. Aside from total expenditure, a significant amount of research has been done on how the share of expenditure for goods varies with income. As far back as 1857, Engel found that the budget share for food decreases as household income increases (Engel, 1857, 1895). More recently, ONS figures (ONS, 2008) indicated that households in the highest income decile spend a greater proportion of their expenditure on ‘transport’ and ‘education’ while spending a smaller proportion on ‘housing’ and ‘food’ compared to the lowest income decile.
4.2 Data source
In order to investigate the relationship between household income and expenditure, keeping demographic characteristics constant, it is necessary to have some information on expenditure patterns that can be linked to household parameters such as the number of people in the household, their ages etc. In the UK, the Expenditure and Food Survey (EFS) provides data on around 2000 spending categories and includes a set of demographic variables describing household characteristics. This makes it suitable for use as the base data set for the model and avoids the need to combine data from more than one source.
The EFS is an annual cross-sectional survey that collects detailed information on household spending obtained from respondents keeping a diary of all spending over a two-week period, combined with retrospective interviews to cover large, occasionally purchased items. Its sample size is around 6,000 households containing over 10,000 individuals. Household and individual level weights are provided so that the survey sample is representative of the UK population. The illustrative model described below restricts itself to the 12 high-level expenditure groups defined in the EFS, which correspond to the Classification of Individual Consumption by Purpose (COICOP) categories (UN, 2013). Table 1 provides a brief summary of each type and some notes on what is included.
Primary EFS expenditure categories.
| Variable name | EFS Household Expenditure Category | Notes |
|---|---|---|
| P601t | Food & non-alcoholic drinks | |
| P602t | Alcohol, Tobacco & Narcotics | Alcohol to be consumed at home |
| P603t | Clothing and Footwear | |
| P604t | Housing Fuel & Power | Includes rent, maintenance of household, water and fuel bills.
Excludes mortgage costs |
| P605t | Household Furnishings & equipment | Includes carpets, curtains, household appliances, utensils and tools |
| P606t | Health | Prescriptions, glasses, dentist fees but not medical insurance |
| P607t | Transport | Purchase of vehicles, fuel, vehicle maintenance but not insurance |
| P608t | Communications | Mobile and fixed line telephone, postage but not internet subscription |
| P609t | Recreation & Culture | Television, computers, CDs, boats, caravans, pets, sports, holidays |
| P610t | Education | Course fees, school trips |
| P611t | Restaurants & Hotels | Includes takeaways, alcohol consumed outside the home and school meals |
| P612t | Miscellaneous | Includes insurance, jewellery, child care, fees, moving expenses |
4.3 Model description
4.3.1 Software platform
Modelling the effect of income and demographics on household expenditure patterns presents a number of requirements. The first is to load in a cross-sectional population. Next, the random assignment element is run for one or more cycles. Finally, aggregate measures are output.
The decision to use an agent-based modelling (ABM) platform to create the model was motivated by the presence of a number of features that reduce the workload of developing the software. Prominent among these is that they provide a convenient way to handle the microsimulation units such as creating, deleting, selecting particular units and changing their internal variables. Following a review of freely available ABM platforms, NetLogo (Wilensky, 1999) was chosen, largely on the basis of its simple yet powerful scripting language. In addition, it has straightforward file input/output facilities and an efficient graphical user interface. This made it easy to use while still offering all the functionality needed to develop the model.
4.3.2 Implementation
An overview of the program algorithm is shown below depicting the main stages of the simulation.
load cross-sectional household data file from the EFS
for each simulated year
for each household
increase income by chosen percentage
for each household
locate a donor household that has a similar composition
and previous income, similar to the current household’s new income
copy expenditure pattern from donor
calculate new aggregated expenditures for categories of interest
4.3.3 Matching criteria
One of the essential features of this algorithm is to locate a similar household. There are many ways this can be done and the selection of which particular method to use will depend on the application and available data. O’Hare (2000) describes several approaches for matching similar cases. These include minimum distance matching, where the donor case is chosen due to its closeness on one or more parameters. A common distance function is the normalised Euclidian distance √∑(xi - yi)2 where xi and yi are the parameters for case i. This can be extended for as many parameters as required. One of the advantages of minimum distance matching is that it can be used on continuous data. If the data are categorical, matching can take place by random selection of a donor case within the same class. These methods can be combined in matching by minimum distance within classes. A further option that could be explored is to use cluster analysis to define equivalence classes and select the donor case from within the appropriate cluster. In the simulation described here, matching takes place using household income, the number of people in the household and a derived variable known as household type. In O’Hare’s classification, this is minimum distance within classes.
The essential feature of this model is that whenever a household experiences a change in income, the expenditure pattern is copied from a similar household that has already had the new income and has had time to adapt. As a result, income, by definition, will be one of the matching criteria. It is represented as if it were a continuous variable so there are no income bands. In many cases, there is not an exact match for a particular income so it is necessary to find the closest alternative. In this implementation, for half of the cases (selected by a random draw), the household with the next higher income is selected as the donor. In the other half, the next lower income household is used. If more than one household satisfies the matching criteria, one of them is selected at random.
Since incomes become more widely separated towards the top of the income distribution, there is a possibility that in some cases, a small intended increase in income can lead to a large jump in that copied from the next higher donor. To reduce this effect, a limit was put in place so that donor incomes cannot be more than twice the intended percentage change in household income. If there are no appropriate donors, all expenditures are changed in proportion to the desired income change and no copying is done for that household in the current cycle.
Households have many characteristics apart from their income and expenditure pattern. One of these is the number of people in the household and it is known that this is correlated with household income (OECD, 2012). If the only matching criterion were income, then selected donor households would be more likely to come from those that have a greater number of occupants. Since households are unlikely to adapt to increasing incomes by taking in new members, this effect was removed by including the number of occupants in the matching criteria.
Household income may also be correlated with the age and sex of occupants. This was controlled for by classifying households by their composition. The following household types were defined and each household was assigned to one of them.
| Type | Description | Definition |
|---|---|---|
| 1 | One person non-pensioner | one person below pensionable age |
| 2 | One person pensioner | one person of pensionable age |
| 3 | Couple with no children | two adults |
| 4 | Family with children | two adults + 1 or more children |
| 5 | Single parent | one adult + 1 or more children |
| 6 | Other | all other households |
(For the purposes of this model, an individual is considered to be an adult if they are aged 16 or over and a child if under 16. Males aged 65 and over are considered pensionable as are females aged 60 or over.)
In order to simulate the effect of changing household incomes, a scenario is run where all households receive a fixed percentage change in income. Processing continues until all households have had their income changed or when the mean income of the population has been changed by the target amount, whichever comes first. Details of the random assignment procedure are shown below, beginning from the point where all households have been set a desired or target percentage increase in income.
for each household
while mean population income <= target population income
select uniformly distributed random number from 0 to 1
if number <= 0.5 (copy from next higher income household)
if any other households with (income >= target) and (increase <= limit) and same type and number in household
store donor expenditure pattern
else
change all spending categories in proportion to income change
if number > 0.5 (copy from next lower income household)
if any other households with (income <= target) and (increase <= limit) and same type and number in household
store donor expenditure pattern
else
change all spending in proportion to income change
for each household
update expenditure patterns from stored donor
The source code and further details of the model can be found in the OpenABM model library http://www.openabm.org/
4.3.4 Running the model
In order to run a simulation, it is first necessary so set up some user defined parameters. These are the number of cases to read from the input file, the number of cycles of random assignment to run and the percentage change in real household income per cycle. It is possible to vary the rate of income change to represent a particular scenario either via a slider on the user interface or in the program code. The output appears in graphical form on the screen or optionally can be written to a file for later analysis.
4.4 Results
4.4.1 The average household
When the initial data file, taken from the 2006 EFS, was read in, mean household income (before tax and including any benefits) was £656. This was increased in a series of 10 steps (10 cycles of random assignment) until it reached £1057, which represents a 61% increase. During this time, mean total consumption expenditure rose from £478 to £654, which is an increase of 37%. This is in agreement with the first two stylised facts, identified above, that expenditures rise with rising income but at a slower rate. As mentioned earlier, the additional income goes partly on income tax, some is saved or invested and some is spent on non-consumption items. This includes mortgage interest payments, which appear in the EFS category ‘other expenditure’. In addition, capital repayment of mortgage is not counted as consumption expenditure.
The output from the simulation takes the form of a cross-sectional population of households and individuals within them. This is the same format as the original input file and enables a high level of flexibility in the analysis of the results. The output can be written to a micro level data-file and examined using a statistics package or represented graphically to highlight trends. The output could also be used as input for further transformations of the population. For example, an employment module could be added and expenditures copied from similar households that have the same number of working and unemployed members. A demographic module could be set up to represent the effect of population change with expenditure patterns copied from households with a similar composition.
It would not be appropriate to write out the disaggregated output dataset here. The following aggregated summary shows how the population reacts to increases in household income. This can be compared against the stylised facts mentioned above to verify that the model produces the expected results.
Table 2 shows expenditure changes for the average household. The ‘Initial Share’ is the proportion of total consumption expenditure that the average household spent on each category at the start of the simulation. The ‘Final Share’ is the budget share for the item after incomes were inflated as described above. ‘Shift in Budget Share’ is the difference between the initial and final share. Due to the stochastic nature of the simulation, there is some variation from one run to the next. As a result, it is not possible to know whether the results from a single instance are typical or unusual. Running the simulation a few times will provide information on how much random variation takes place between runs. This can be quantified in a number of ways such as calculating the difference between maximum and minimum values of the output for a particular parameter, obtained from a number of runs or from their standard deviation. It is also possible to calculate confidence intervals for the results and the next column of Table 2 gives the 95% confidence interval of the final budget share for each expenditure category. The last two columns of Table 2 show the upper and lower bounds of the confidence intervals. The results are the mean of three simulations. The variation is assumed to be normally distributed because the process generating the deviations is the random assignment scheme itself. While this gives some indication of the variability of the model, it gives no indication of the accuracy of the model specification.
Share of expenditure with increasing income (all households).
| Expenditure Category | Initial Share (%) | Final Share (%) | Shift in Budget Share (%) | 95% Confidence Interval (+ −) α = 0.05, n = 3 | Lower CI | Upper CI |
|---|---|---|---|---|---|---|
| Transport | 13.00 | 13.94 | 0.95 | 0.288 | 13.65 | 14.23 |
| Education | 1.48 | 2.31 | 0.82 | 0.242 | 2.07 | 2.55 |
| Furniture | 6.32 | 6.58 | 0.26 | 0.200 | 6.38 | 6.78 |
| Miscellaneous | 7.54 | 7.63 | 0.09 | 0.152 | 7.48 | 7.78 |
| Health | 1.24 | 1.31 | 0.07 | 0.033 | 1.28 | 1.34 |
| Clothing | 4.86 | 4.79 | −0.08 | 0.095 | 4.70 | 4.89 |
| Hotels | 7.92 | 7.79 | −0.13 | 0.007 | 7.78 | 7.80 |
| Communication | 2.46 | 2.1 | −0.36 | 0.017 | 2.08 | 2.12 |
| Recreation | 12.26 | 11.89 | −0.37 | 0.325 | 11.57 | 12.22 |
| Alcohol | 2.33 | 1.94 | −0.39 | 0.039 | 1.90 | 1.98 |
| Housing | 9.94 | 8.92 | −1.02 | 0.167 | 8.75 | 9.09 |
| Food | 9.81 | 8.14 | −1.67 | 0.059 | 8.08 | 8.20 |
-
The expenditure shares to not add up to 100% because some spending goes to other items not included in these categories.
Table 2 is sorted into descending order of percentage change so that as incomes rise, households devote a greater proportion of their consumption expenditure to the goods near top of the list. These categories can be said to have a greater discretionary element than those lower down.
Table 2 indicates that the categories of ‘education’ and ‘transport’ receive a greater share of the increased expenditure than the other items. This is consistent with the ONS results mentioned above, which showed that households in the highest income decile spend more of their income in these categories than those in the lowest income decile.
At the bottom end, ‘food’ and ‘housing’, receive a diminishing share of the rising income, which is consistent with what was reported by the ONS. Finally, the budget share for ‘food’ falls as incomes rise and this is in agreement with Engel’s Law.
These results are not surprising. They are merely intended to verify that the model produces the expected results. However, the micro-level cross-sectional output can be analysed in a variety of ways and the next section shows trends in more detail and later compares the results among subsections of the population.
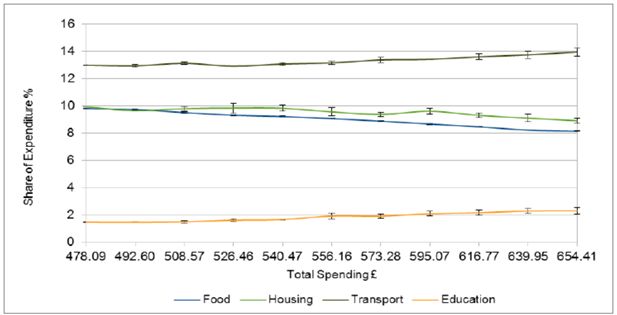
Figure 1 shows the results at regular points during the simulation. The share of consumption expenditure is given as a percentage, on the y-axis. Only the top two and bottom two items from Table 2 are plotted. This makes them easier to see and these are the items that exhibited the most variation. The 95% confidence intervals are shown for each data point and indicate that random variation is relatively small in this simulation.
It can be seen that the lines are not monotonic and there is variation in the magnitude and direction of change from cycle to cycle. This is due to the stochastic nature of the model where the results are influenced by the characteristics of which particular donors happen to be selected in the course of each cycle. The random variations tend to cancel out over time and this is why it is preferable to complete the income change in a number of small steps rather than in one jump.
The next two sections provide further results for selected sections of the population that can be expected to have differing expenditure patterns. The first of these compares ‘older households’ and ‘families with young children’ with the average household in Section 4.4.2. After this, Section 4.4.3 gives results disaggregated by income quintile.
4.4.2 Comparison of the average household with older households and families with young children
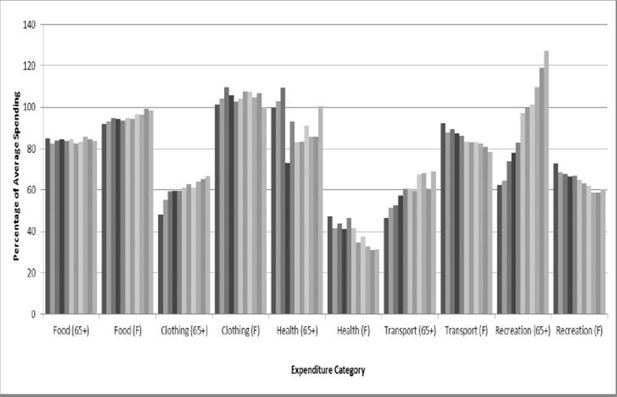
Figure 2 shows changes in spending patterns for two types of household:
those with at least one person aged over 65 (older households);
households with one or more children under 5 (families with young children).
In each case, incomes were inflated in the same way as in the previous simulation, then spending in pounds per week, for each good, was divided by the square root of the number of people in the household to compensate for household size (Buhmann et al., 1988). Next, the amount spent on each expenditure item was divided by the amount spent on that good by the average household so that the results are shown as a percentage of what the typical household spends.
The expenditure categories are shown on the x-axis: first for the older households (65+) and then for the family with young children (F). Each individual bar represents spending at each step of the simulation as incomes were increased.
These results were obtained from one simulation so there are no confidence intervals. However, the amount of variation between each cycle of random assignment can be seen in the level of irregularity between the columns within each expenditure category.
For the ‘food’ category, it is apparent that households in which at least one member is aged over 65, spend about 80% of what the average household spends. As incomes rise, this figure is largely unchanged which indicates that this group increase spending on food at about the same rate as the average household. The family with children under 5, spend more than this initially and increase spending more rapidly as incomes rise, almost reaching the same level as the average household by the end of the simulation.
The older households spend slightly over 60% of the average on ‘recreation’ at the start of the simulation. The rate of increase is much faster than the average household and reaches over 120% of average spending after incomes were inflated. By contrast, the family with young children allocate less spending than the average household to this category as incomes rise. This leads to a decline in budget share for ‘recreation’ compared with the average household. In this way, the graph gives an indication of the relative priority of allocating the extra spending due to rising incomes.
4.4.3 Analysis by household income quintile
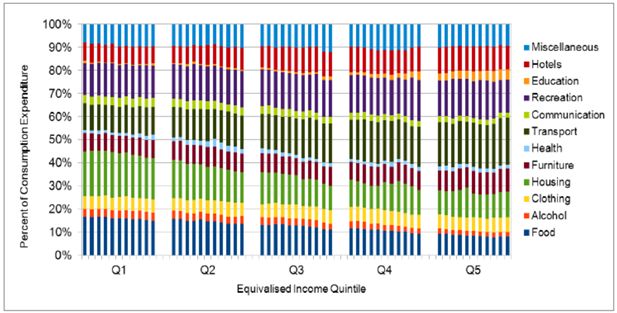
Figure 3 shows changes in spending patterns by quintile as incomes rise, with quintile 1 being the lowest income group and quintile 5 being the highest. This is equivalised as before by dividing income and spending by the square root of household size. Results are presented for all 12 of the EFS high-level categories, as a percentage of the total spending among these categories.
In Table 2 above (Section 4.4.1), ‘education’ was identified as experiencing one of the largest increases in budget share. Figure 3 shows that the increase is moderate in the lower three quintiles. Much of the change appears in quintile 4 and for quintile 5, ‘education’ forms a significant budget item. Spending on ‘transport’ increases throughout to almost double its share between quintile 1 and 5.
The budget share for ‘housing’ declines as incomes rise, with much of this taking place in the lowest three quintiles. The proportion spent on ‘food’ declines as would be expected from Engel’s Law.
5. Discussion
This example shows how a random assignment scheme can be applied to model a set of several goods at a disaggregated level. The matching scheme used here selects a donor case and from there, any variables from the donor can be copied to the receiver. As a result, there is no restriction on the number of goods that can be modelled. In principle, every item in the EFS could be represented and the complexity of the model would rise linearly with the number of goods. Also, since the individual households are retained, the distribution of variables is preserved and output can be produced at the micro-level.
This does not mean the method is without pitfalls. As was mentioned above, selecting cases on a parameter such as increasing income means that all the variables from the case will be available for copying and some of these will be correlated with income. If the change in income really causes the change in another variable, this can be used to determine the effect of the former on the latter. However, if the change in income does not cause the change, such as when income does not cause household size to increase, this will lead to an inaccurate estimation of the effect because the simulated households change in a way that real households do not. This can be minimised by including more variables in the matching criteria to limit the household’s response to changing conditions. A sensitivity analysis can be done by adding matching criteria, one by one, until the change in output reduces to an acceptable level. A regression of the matching variables on the output variables will indicate how much of the variation is explained by the model and so give an indication of its reliability. The problem of model specification is not unique to random assignment and all modelling methods can be done well or badly whatever approach is taken.
Although random assignment preserves the individual cases, the model described above does not model trajectories. It is based on a cross-sectional dataset and assumes that households will respond to a change in circumstances by adjusting their spending patterns to become more like those that have already experienced the new conditions. This may have some plausibility but it is also reasonable to suppose that households would try to retain as much of their original behaviour as possible. It would be feasible to model this by using a longitudinal dataset and copying from donors that have experienced a similar change over time. Unfortunately, the EFS is a repeated cross-sectional survey and there are currently no large-scale longitudinal panel surveys, in the UK at least, that monitor detailed household spending categories over time.
Random assignment is related to statistical matching, which is used in microsimulation to combine data from a number of different sources or files. Here, individual cases are matched on the basis of the similarity between one or more variables which are common to both sources (Ingram et al., 2001). However, the random assignment scheme applied in this paper is essentially different from statistical matching because records are matched from within the same dataset. This makes it more akin to hot deck imputation where missing variables are obtained from a similar case that has a complete set of variables (Andridge & Little, 2010). Hot deck imputation is often used in surveys, where respondents may decline to answer some or all of the questions. This is particularly problematic because different respondents may have different propensities for omitting data so leading to biased results. A range of methods has been developed to ameliorate this problem such as propensity score matching (Rosenbaum & Rubin, 1983) and multiple imputation (Rubin, 1987). Here, the imputation process is repeated a number of times account for the variability or uncertainty in the results, which is lost in a single imputation. This allows an accurate statistical description of the resulting micro-level data file to be made. The model described above also made use of multiple runs to average out the random element of the imputation. This invites the possibility of combining the two approaches and further work in this area may prove fruitful.
6. Conclusion
Modelling household expenditure is usually done by econometric methods but there are some difficulties with this approach. These include the problem of modelling at a highly disaggregated level and limits on the number of goods that can be represented. The example model described in this paper shows that a random assignment scheme provides one way to avoid these limitations. The paper set out to illustrate the practical advantages of random assignment and the results point to areas for further research such as the possibility of matching using longitudinal data and applying multiple imputation.
References
-
1
Household Demand in Turkey: An Application of Almost Ideal Demand System with Spatial Cost Index. Working Paper 0226, ERF Working Paper SeriesCairo: Economic Research Forum.
-
2
A Review of Hot Deck Imputation for Survey Non-responseInternational Statistical Review 78:40–64.https://doi.org/10.1111/j.1751-5823.2010.00103.x
-
3
Equivalence Scales, Well-Being, Inequality, and Poverty – Sensitivity estimates across 10 countries using the Luxembourg Income Study (LIS), databaseReview of Income and Wealth pp. 115–142.
- 4
- 5
-
6
Das Lebenskosten belgischer Arbeiterfamilien frÄuher und jetztBulletin de Institut International de Statistique 9:1–124.
- 7
-
8
Imitation or Interaction in Spatial Micro Simulation2nd General Conference of the International Microsimulation Association.
-
9
Statistical Matching: a new validation case studyProceedings of the Section on Survey Research Methods, American Statistical Association pp. 746–751.
-
10
MICROHUS. A Micro-simulation Model for the Swedish Household Sector. A Progress ReportPaper presented at the, International Symposium on Economic Modelling, August 18–20, Gothenburg, Sweden.
-
11
Micro-simulation and Public PolicyDirect and behavioural effects of income tax changes -simulations with the Swedish model MICROHUS, (ed.), Micro-simulation and Public Policy, Elsevier Science Publishers, Amsterdam.
-
12
A Survey, Papers 1997-31. Uppsala – Working Paper SeriesA Survey, Papers 1997-31. Uppsala – Working Paper Series.
-
13
What are Equivalence ClassesOECD Project on Income Distribution and Poverty.
-
14
2000 Microsimulation in Government Policy and ForecastingImpute or Match? Strategies for Microsimulation Modelling, (eds.), 2000 Microsimulation in Government Policy and Forecasting, Elsevier, London.
-
15
Family Spending: 2007 Edition, Ed, http://www.ons.gov.uk/ons/rel/family-spending/family-spending/2007-edition/index.htmlFamily Spending: 2007 Edition, Ed, http://www.ons.gov.uk/ons/rel/family-spending/family-spending/2007-edition/index.html.
-
16
http://www.ons.gov.uk/ons/rel/consumer-trends/consumer-trends/q2-2010/index.htmlHousehold Final Consumption Expenditure Summary’ 0.CN, Consumer Trends – Q2 2010.
-
17
The Central Role of the Propensity Score in Observational Studies for Causal EffectsBiometrika 70:41–50.
- 18
- 19
- 20
-
21
http://ccl.northwestern.edu/netlogo/NetLogo.
Article and author information
Author details
Acknowledgements
This research was supported financially by the UK Economic and Social Research Council (ESRC) and BT plc. The work was supervised by Dr. Ben Anderson and I should like to thank the anonymous reviewers for their insightful and constructive comments.
Publication history
- Version of Record published: August 31, 2013 (version 1)
Copyright
© 2013, Lawson
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.