Modelling the impact of declining Australian terms of trade on the spatial distribution of income

The movements in terms of trade (ratio of export to import prices) directly affects a country’s trade activity, which then has implications for growth and income distributions. There is a large and growing literature on the relationship between trade, growth, income distribution and poverty. Berg and Krueger (2003) and Santos-Paulino (2012) provide a useful survey of this literature. Richardson (1995) explores the relationship between trade openness and income inequality. Another related strand of literature focuses on the regional impacts of trade policy (such as trade liberalisation) and shocks (such as movements in terms of trade and foreign demand). For instance, the World Bank (2008) notes the increasing trade activity of a country may lead to higher regional disparities within the country as the areas that have access to ports take advantage of the increased trade.

This is contrary to classical economic theory that states that perfect mobility equalises the economic growth across regions. Henderson (1982) points out that the equalisation mechanism depends on the relative endowment and capacity of different regions in the economy. This argument is supported by Krugman and Livas Elizondo (1996). While a review of the literature by Brulhart (2011) argues that this conclusion may have been too strong, the empirical work by Ezcurra and Rodriguez-Pose (2013) confirms this different spatial effect of trade. In the case of Australia, Behrens et al. (2007) find that the positive impact of trade can be hampered by relatively higher transport costs in mainland rural areas of Australia. Furthermore, greater openness in trade (i.e. the ease of the flow of factors of production and technology in and out of a country) may impact not only on income inequality but also asset inequalities, spatial inequalities, and gender inequalities (Anderson 2005).

Most of the studies on the impacts of trade on inequality and poverty have focused on developing countries (see for instance Kanbur and Venables (2005) for a collection of articles). However, the spatial distribution of a decline in terms of trade in a developed country like Australia is of interest, given the importance of the income gains of the recent boom in terms of trade (largely on the back of a resources boom).

The spatial impacts of these macro shocks such as a decline in terms of trade may be important for a number of reasons. Parliamentary representatives elected from regions for State and Federal governments often demand regional detail in economic and social analysis. Policy makers concerned with regional disparities in employment, income and overall economic opportunities demand detailed regional results, in particular for economic and social impacts on the households and the communities in small areas (Horridge et al., 2005). Other stakeholders (such as unions, NGOs, local community groups and other interest groups) who work with and represent small regions are also interested in the impacts of macro-economic change on their region. Local and regional issues are also important to academics, researchers and modellers who have a responsibility to provide independent analysis to inform policy development that may include the likely impact of a policy or an external shock on local communities.

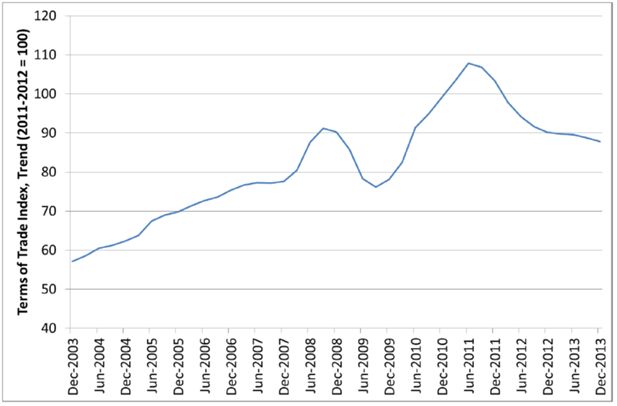
Before the onset of the Global Financial Crisis (GFC), the Australian terms of trade had been on a rising trend for over a decade (Jaaskela & Smith 2013 and see Figure 1). The authors of this paper find that higher terms of trade tend be expansionary but not inflationary. It is worth noting that unlike previous booms in Australian terms of trade such as in the 1920s and 1950s, which were followed by falling output and increased unemployment, the recent increases in the terms of trade created less instability (Battellino, 2010). Gregory points out that the boom in the terms of trade in the last decade or so has raised the average living standards in Australia to above that of US (Gregory, 2012).

Figure 1

Download asset Open asset

Although the Australian terms of trade declined slightly during the GFC, the terms of trade was back to an increasing trend a year after the onset of GFC. However, it has now shown a steady decline since mid-2011 (see Figure 1). Given the benefit that the Australian economy experienced from rising terms of trade, there are concerns that the downward trend could not only harm the economy but also change the income distribution among households in different locations in Australia. It is thus vital that the spatial effects of a steady decline in terms of trade be examined in greater detail.

In this paper, we use a computable general equilibrium (CGE) model, a national microsimulation model and a spatial microsimulation model to capture the impact of a macro shock on the distribution of income in small regional areas of the Australian economy. It is important to note that the standard Computable General Equilibrium (CGE) models do not capture the distributional impact of a policy change or an external shock in small geographical areas. To overcome this limitation, we have sequentially linked a CGE, a microsimulation and a spatial microsimulation model in a top-down manner to capture the distribution of income in small areas. How the models are sequentially linked, including how consistency between the models has been achieved, and the transmission of a macro shock from the macro and sectoral impacts to its distributional impacts in the small geographical regions, is the focus of the paper. To implement the framework we simulate a potential Australian terms of trade decline over a five year period (2012–13 to 2017–18).

With this background, the rest of the paper is organised as follows. The next section describes the modelling framework. Section 3 explains how the terms of trade shock is modelled. Section 4 discusses the results and Section 5 concludes.

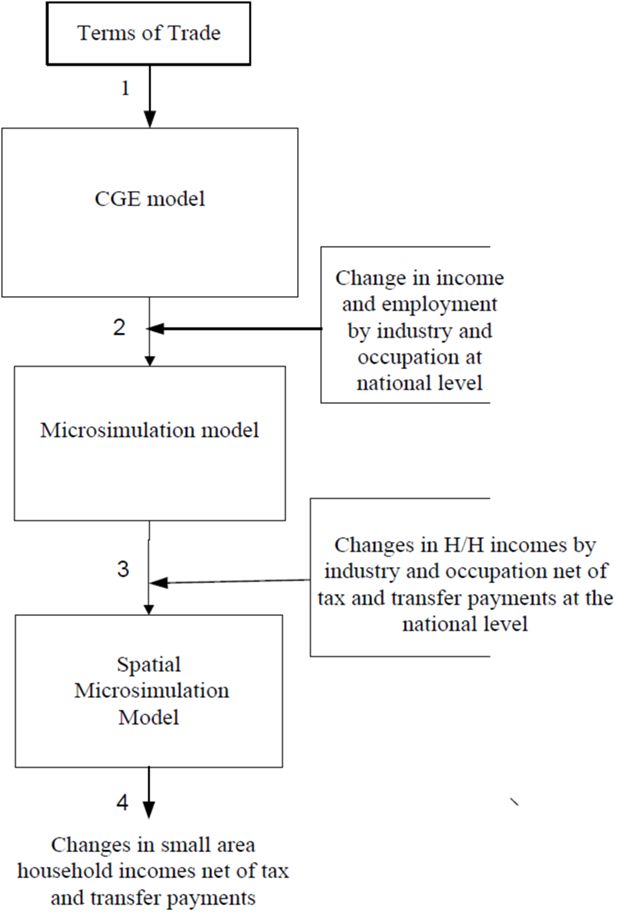
Before developing a model which brings together a number of other models, it is useful to specify an approach that will link the different models. This paper uses the framework developed by Rao et al. (2013) that links a CGE model with a microsimulation and spatial microsimulation model. This link is achieved by linking the CGE output to different types of households through the household members that work in different industries and occupations. Based on these different types of households, this method simulates how tax payments and transfer payments respond to the macro-economic shock provided in the CGE model. The spatial effect is then estimated by distributing the households into small areas using a spatial microsimulation model.

Figure 2 depicts the modelling approach used to simulate the distributional impacts of an Australian terms of trade decline on the Australian and regional households. The terms of trade shock is a macro shock and its economy-wide impacts can be best captured by a computable general equilibrium model as shown by link 1 in Figure 2. We use the ORANI CGE model of the Australian economy (Dixon, et al., 1982) with an extended forecasting feature. The extended model with the forecasting feature is described in detail in Rao (2011). The output of interest of the CGE model is the changes in the employment by industry and occupation resulting of the terms of trade shock (link 2 in Figure 2), which captures the winners and losers in terms of industries and occupations at the national level.

Figure 2

Download asset Open asset

Most national CGE models provide a relatively disaggregated (sectors, occupations, skills/qualifications) representation of the economy. However, traditionally, one or a relatively small number of representative (homogenous) household groups describe the income distribution in most CGE models, and thus do not capture the heterogeneity of households represented in the population (Colombo, 2010). Moreover, CGE models typically do not include complex tax and transfer payment systems present in developed countries like Australia and therefore cannot capture the full impact of a policy or external shock net of tax and transfer payments. For these reasons, CGE models have limited application for distributional analysis.

To capture the full distributional impacts of the TOT shock on households at the national level, including the full application of the Australian tax and transfer payments, we pass the output of the CGE model (changes in factor employment and incomes by industry) to STINMOD – a national tax and transfer microsimulation model of the Australian economy (Lambert, et al. 1994, Percival et al., 2007). STINMOD calculates the distribution of the household income (cross-classified over a number of household characteristics) at the national level (which can be disaggregated into State and Territory levels), after taking into account the tax and transfer payments (link 3 in Figure 2). However, the distribution of household income may not fully represent small geographical areas of interest, given that small areas are not normally captured by national sample surveys on which STINMOD is based. To capture the impacts in small areas we link STINMOD to SpatialMSM, a spatial microsimulation model of the Australian population (Tanton et al., 2011), which derives datasets of small areas using Census data and data from official ABS sample surveys to capture household details in small areas. The output from STINMOD, that is, the distribution of household income at the national or state/territory levels, net of tax and transfer payments, is passed to SpatialMSM to calculate the distribution of household income (cross-classified over a number of household characteristics) in small geographical areas (link 4 in Figure 1).

Table 3 reports the macro results of the terms of trade shock. We use the BOTE model described above to explain these macro effects. Bold letters in the BOTE model indicates that the variables are exogenously determined in the policy simulation. Note that Equations (1) and (2) are reproduced in the BOTE model as Equations 10 and 11 for easy reference. As explained earlier, the source of the terms of trade shock is a fall in the foreign demand for Australian exports. In terms of the BOTE model, there is a negative shock to TOT in Equation 10 causing a leftward shift in the export demand schedule (a negative movement in V) inducing declines in both foreign currency price of exports (P_X) and the volume of exports (X). The fall in P_X induces the fall in TOT via equation 11. The effects of the fall in TOT of 22.6 percent (row 18, Table 3) are traced as follows.

Given that L, ROR and A fixed in Equation 4, the decline in TOT will cause a decline in K (row 13), since K is positively related to TOT. With A and L exogenous in Equation (4), the decline in K will cause real GDP to fall (row 1). The declines in GDP and TOT cause GNP to decline (row 3) via Equation 7. The decline in GNP, with APC and Γ fixed causes both private and public consumption to fall via Equations 5 and 6 (rows 6 and 7) respectively.

Given that L, ROR and A are fixed in Equation 4, the decline in TOT will cause a decline in K (row 13), since K is positively related to TOT. With A and L exogenous in Equation (4), the decline in K will cause real GDP to fall (row 1). The declines in GDP and TOT cause GNP to decline (row 3) via Equation 7. The decline in GNP, with APC and Γ fixed causes both private and public consumption to fall via Equations 5 and 6 (rows 6 and 7) respectively. A decline in K with Ψ exogenous implies a fall in investment (I) via Equation 12 (row 8). With C, G and I determined, so is absorption or GNE (row 2). Note that GNE declines faster than GDP, which via Equation 3, implies that the trade balance (X-M) must move towards surplus (row 22). Thus, imports decline (row 10) and exports increase (row 9), facilitated by a real exchange rate depreciation (row 16). The decline in imports is explained by the BOTE Equation 9, that is, the declines in GDP and TOT both cause imports to fall, given that both GDP and TOT are positively related to GDP. Equation 14 shows that the declines in K and TOT, with A fixed causes the economy-wide wage rate (W) to fall, which will have significant implications for spatial distribution of employment and income discussed later in this paper.

4.3 The regional effects

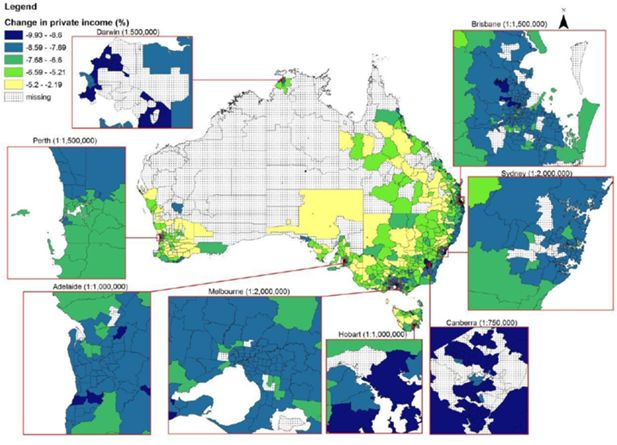
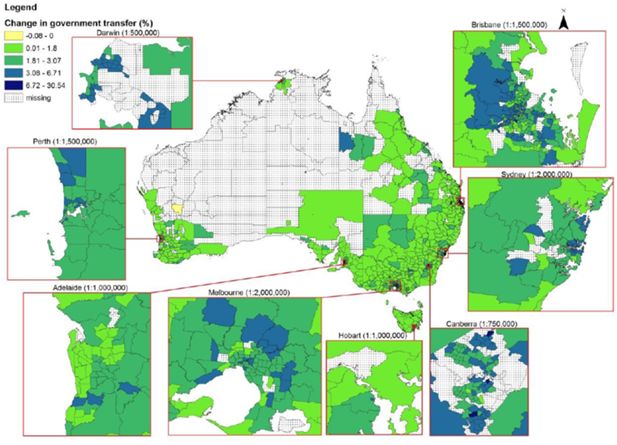
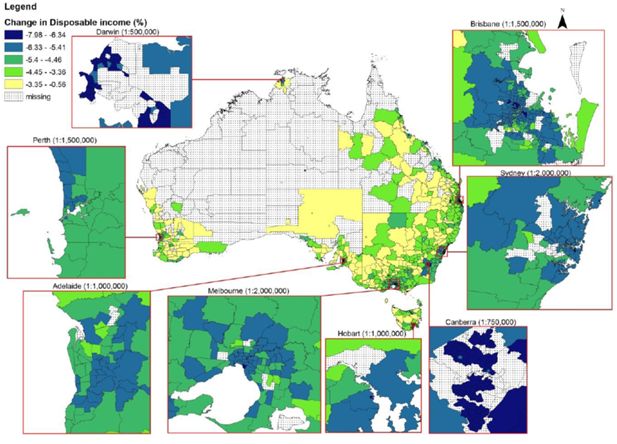
The spatial effect of the TOT shock, estimated using the SpatialMSM model, is shown in Figure 3. This figure depicts the impact in a choropleth map with the darker colour indicating the higher impact. The classification ranges for this map use natural breaks where the different classification is determined by the largest difference between two subsequent changes in the distribution. This classification is often used for identifying clusters as well as separating the relatively high impacts from low ones. The shaded (dotted) areas in the middle of Australia are areas where our spatial microsimulation model was not able to derive estimates due to non-convergence (see above).

Figure 3

Download asset Open asset

Given that the three sectors experiencing the greatest drop in wage rates as a result of the drop in TOT are Retail Trade, Health-Social Services and Construction, we would expect Capital Cities in Australia, where these sectors are larger, to experience a greater impact of the drop in TOT on gross income. The regional effect of the change in the TOT confirms this expectation with a darker colour showing areas with greater decreases. The figure indicates that the greatest decrease in gross income will be in Canberra, Darwin and the areas surrounding Hobart while Sydney, Brisbane, Melbourne, Adelaide and Perth experience a lower decrease. In Perth, the impact is estimated to be mainly in the North part of the city. In contrast, the impact on Canberra seems to be spread around the surrounding areas from where commuters that work in Canberra come from.

Besides capital cities, Figure 3 also indicates that the east coast of Australia will experience a considerable impact. This is especially true for the south east coastal area of NSW to Brisbane in Queensland.

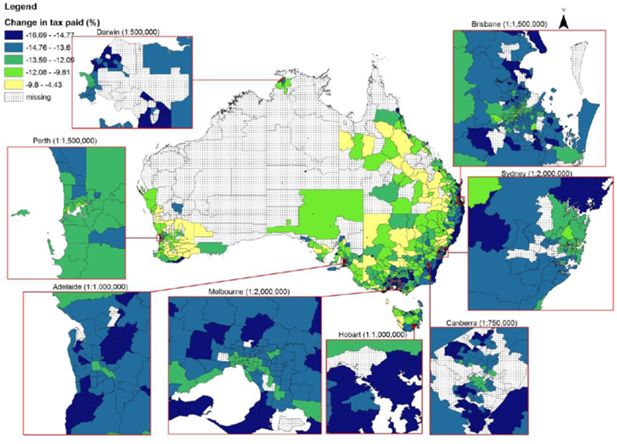
The greater impact on the incomes of households in Canberra, Darwin and Hobart does not mean that the tax reduction will come from those cities. The income structure will play an important role in determining the reduction in tax paid. Figure 4 shows that the area surrounding Hobart experiences a higher reduction in tax paid and also identifies areas such as Gosford and the Blue Mountains in the North and West of Sydney, respectively, as having a greater reduction in tax paid than other areas. This is also true for the areas surrounding Melbourne, Brisbane, Adelaide and Canberra. In addition, areas on the South East Coast are estimated as experiencing greater drops in tax paid compared to capital cities. In contrast, areas experiencing a lower reduction in tax paid are relatively wealthy areas such as North Sydney and inner city areas of Melbourne, Brisbane, Canberra and Adelaide. The reduction in tax paid in Perth is estimated to be much lower than other capital cities.

Figure 4

Download asset Open asset

The next variable we looked at from the microsimulation models was Government transfer payments (Figure 5). Although the income structure plays a role in Government transfer payments, income is not the only factor determining transfer payments, so changes in Government transfer payments are more likely to be determined by the distribution of different household characteristics among regions in Australia. As a result, our estimation does not indicate a huge difference in changes to Government transfer payments between areas. The relatively higher increase in capital cities is more likely due to the greater fall in the household incomes in those areas. The impact also seems to be spread more evenly around capital cities. There are some suburbs in Melbourne, Brisbane and Canberra that we estimate will receive higher increases in transfer payments. One argument that can be offered for this is the spread of children in these areas. For example, Gungahlin in the North of Canberra and Tuggeranong in the South of Canberra have relatively high increases. Both these are fairly new areas with a higher proportion of young families.

Figure 5

Download asset Open asset

Finally, we look at the changes in disposable income (Figure 6). Disposable income is the amount that is available for households to spend on goods and services, so it takes out tax paid from gross income. One of the advantages of the type of analysis used for this model is that disposable incomes can be calculated from the base dataset. One of the major differences between the change in disposable income compared to the change in gross income is that the East Coast area no longer experiences a large drop in disposable income. This is likely due to the large tax reduction estimated for the area. The estimated tax reduction has also reduced the reduction in incomes in capital cities such as Sydney, Melbourne, Adelaide, Hobart, and to some extent Brisbane and Perth. This means the income fall is mainly concentrated in Canberra and to a lesser extent Darwin.

Figure 6

Download asset Open asset

Macro-economic shocks can have different spatial impacts across the country depending on resource endowments, physical and human capital among other factors. The final impacts on households will depend on the characteristics of each household and the national tax transfer system. In this paper, we combine a CGE, a tax-transfer microsimulation model and a spatial microsimulation to transparently trace the spatial distribution of the impacts of a terms of trade decline.

In particular, we find that capital cities are most affected by a decline in the TOT. The industries most affected are retail, construction and health and social services sectors, all of which are largely located in capital cities. Since the CGE model is linked to a tax/transfer microsimulation model, it enabled us to compute tax paid, Government transfer payments disbursed; and finally disposable income. We find that government transfer payments were not as affected by the TOT decline compared to income and tax paid as these payments are not entirely dependent on incomes. This linking of CGE and microsimulation models is a useful framework, as it is able to show the regional/spatial impacts of a macro-economic policy or external shock that enables policy makers and researchers to identify the areas affected most by such shocks.

The model described in this paper has some limitations. The main limitation is that the model relies on the distribution of income by industry and occupation among household members and small geographic areas to distribute the impact of the TOT decline at a national level. This means that the relationship between economic sectors at the local level is assumed to be in line with the relationship at the national level. This may not always be true as the market behaviour in regional areas can be different to the national market behaviour. In addition, the relationship between different regions has only been captured by the relationship between different industrial sectors. Therefore, the issue of whether market behaviour changes due to clustering of areas within a certain industrial sector has not been assessed by the model.

The other limitation is that the microsimulation model used in this paper is static and only estimates the immediate impact from the decline. Long term estimates of the impact would create some challenges. For example, people in different areas that suffer similar impacts may respond differently as they could have different levels of resilience. Furthermore, the response may affect the CGE modelling, for example, through changes in consumption and this means the model would need some iterative interaction between the CGE and microsimulation model.

In this paper, we have been able to show how a CGE, microsimulation and spatial microsimulation can be linked. While this has been shown in this paper, there is still further development required. Other macro-economic shocks can be modelled, and behavioural responses could be incorporated into the model. Further, the CGE model is still a national model, and assumes national relationships between industries – this assumption could be relaxed using a regional CGE model.

1. 1
   Openness and inequality in developing countries: A review of theory and recent evidence

   1. E Anderson

   (2005)

   World Development 33:1045–1063.

   • Google Scholar
2. 2
   Mining Booms and the Australian Economy

   1. R Battellino

   (2010)

   Address to The Sydney Institute, Sydney.

   • Google Scholar
3. 3
   Countries, regions and trade: On the welfare impacts of economic integration

   1. K Behrens
   2. C Gaigne
   3. GI Ottaviano
   4. JF Thisse

   (2007)

   European Economic Review 51:1277–1301.

   • Google Scholar
4. 4
   GREGWT and TABLE Macros—Users Guide

   1. P Bell

   (2000)

   Australian Bureau of Statistics, Canberra.

   • Google Scholar
5. 5
   Trade, Growth and Poverty: A Selective Survey. IMF Working Paper

   1. A Berg
   2. A Krueger

   (2003)

   Washington, DC: International Monetary Fund.

   • Google Scholar
6. 6
   The spatial effects of trade openness: A survey

   1. M Brulhart

   (2011)

   Review of World Economics 147:59–83.

   • Google Scholar
7. 7
   Linking a microsimulation model to a dynamic cge model: Climate change mitigation policies and income distribution in australia

   1. H Buddelmeyer
   2. N Hérault
   3. G Kalb
   4. MVZ de Jong

   (2012)

   International Journal of Microsimulation 5:40–58.

   • Google Scholar
8. 8
   Linking CGE and Microsimulation Models: A Comparison of Different Approaches

   1. G Colombo

   (2010)

   International Journal of Microsimulation 3:72–91.

   • Google Scholar
9. 9
   Contributions to Economic Analysis

   1. PB Dixon
   2. BR Parmenter
   3. J Sutton
   4. DP Vincent

   (1982)

   Contributions to Economic Analysis, 142, North-Holland Publishing Company, Amsterdam.

   • Google Scholar
10. 10
    Dynamic general equilibrium modelling for forecasting and policy: a practical guide and documentation of MONASH

    1. PD Dixon
    2. MT Rimmer

    (2002)

    Amsterdam: Elsevier Science B.V.

    • Google Scholar
11. 11
    Does Economic Globalization affect Regional Inequality? A Cross-country Analysis

    1. R Ezcurra
    2. A Rodriguez-Pose

    (2013)

    World Development 52:92–103.

    • Google Scholar
12. 12
    The effects of recent structural, policy and external shocks to the Australian economy, 1996/97-2001-02. Australian Economic Papers

    1. J Giesecke

    (2008)

    15–37, The effects of recent structural, policy and external shocks to the Australian economy, 1996/97-2001-02. Australian Economic Papers, 47.

    • Google Scholar
13. 13
    Living standards, terms of trade and foreign ownership: reflections on the Australian mining boom

    1. RG Gregory

    (2012)

    Australian Journal of Agricultural and Resource Economics 56:171–200.

    • Google Scholar
14. 14
    Improving work incentives for parents: the national and geographic impact of liberalising the Family Tax Benefit income test

    1. A Harding
    2. QN Vu
    3. R Tanton
    4. Y Vidyattama

    (2009)

    The Economic Record 85:48–58.

    • Google Scholar
15. 15
    Systems of cities in closed and open economies

    1. JV Henderson

    (1982)

    Regional Science and Urban Economics 12:325–350.

    • Google Scholar
16. 16
    The impact of 2002-03 drought on Australia

    1. M Horridge
    2. J Madden
    3. G Wittwer

    (2005)

    Journal of Policy Modeling 27:285–308.

    • Google Scholar
17. 17
    Terms of Trade Shocks: What Are They and What Do They Do?

    1. J Jaaskela
    2. P Smith

    (2013)

    Economic Record 89:145–159.

    • Google Scholar
18. 18
    Spatial inequality and development

    1. R Kanbur
    2. AJ Venables

    (2005)

    Oxford: Oxford University Press.

    • Google Scholar
19. 19
    Journal of Development Economics

    1. P Krugman
    2. R Livas Elizondo

    (1996)

    137–150, Journal of Development Economics, 49.

    • Google Scholar
20. 20
    An introduction to STINMOD: a static microsimulation Model. NATSEM Technical Paper No 1

    1. S Lambert
    2. R Percival
    3. D Schofield
    4. S Paul

    (1994)

    Canberra: University of Canberra.

    • Google Scholar
21. 21
    STINMOD (static income model) 2007

    1. R Percival
    2. A Abello
    3. QN Vu

    (2007)

    In: A Gupta, A Harding, editors. Modelling our future: population ageing, health and aged care. Amsterdam: Elsevier BV. pp. 477–82.

    • Google Scholar
22. 22
    A Systems Approach to Analyse the Impacts of Water Policy Reform in the Murray-Darling Basin: a Conceptual and an Analytical Framework. NATSEM Working Paper 2013/22

    1. M Rao
    2. R Tanton
    3. Y Vidyattama

    (2013)

    Canberra, Australia: University of Canberra.

    • Google Scholar
23. 23
    ORANI-ED: A CGE Model of the Australian Economy for Labour Market Forecasting and Education and Training Sector Policy Analysis

    1. M Rao

    (2011)

    ORANI-ED: A CGE Model of the Australian Economy for Labour Market Forecasting and Education and Training Sector Policy Analysis, Unpublished PhD Thesis, Faculty of Business and Economics, Centre of Policy Studies, Monash University, http://arrow.monash.edu.au/hdl/1959.1/540569.

    • Google Scholar
24. 24
    Income inequality and trade: how to think, what to conclude

    1. JD Richardson

    (1995)

    Journal of Economic Perspectives 9:33–55.

    • Google Scholar
25. 25
    Trade, Income Distribution and Poverty in Developing Countries: A survey. Discussion Paper No. 207, UNCTAD

    1. AU Santos-Paulino

    (2012)

    New York: United Nations.

    • Google Scholar
26. 26
    Understanding calibration estimators in survey sampling

    1. AC Singh
    2. CA Mohl

    (1996)

    Survey Methodology 22:107–115.

    • Google Scholar
27. 27
    Old, single and poor: using microsimulation and microdata to analyse poverty and the impact of policy change among older Australians

    1. R Tanton
    2. Y Vidyattama
    3. J McNamara
    4. QN Vu
    5. A Harding

    (2009)

    Economic Papers: A Journal of Applied Economics and Policy 28:102–120.

    • Google Scholar
28. 28
    Small area estimation using a reweighting algorithm

    1. R Tanton
    2. Y Vidyattama
    3. B Nepal
    4. J McNamara

    (2011)

    931–951, Journal of the Royal Statistical Society Series A, (Statistics in Society), 174.

    • Google Scholar
29. 29
    World development report 2009: Reshaping economic geography

    1. World Bank

    (2008)

    Washington, DC: World Bank.

    • Google Scholar

Author details

1. Yogi Vidyattama

   National Centre for Social and Economic Modelling (NATSEM), Institute for Governance and Policy Analysis, University of Canberra, Australia

   For correspondence

   yogi.vidyattama@canberra.edu.au

2. Maheshwar Rao

   National Centre for Social and Economic Modelling (NATSEM), Institute for Governance and Policy Analysis, University of Canberra, Australia

   For correspondence

   maheshwar.rao @canberra.edu.au

3. Itismita Mohanty

   Centre for Research and Action in Public Health, University of Canberra, Australia

   For correspondence

   itismita.mohanty @canberra.edu.au

4. Robert Tanton

   National Centre for Social and Economic Modelling (NATSEM), Institute for Governance and Policy Analysis, University of Canberra, Australia

   For correspondence

   robert.tanton@canberra.edu.au