
Measuring small area inequality using spatial microsimulation: Lessons learned from Australia
Abstract
Measuring income inequality has long been of interest in applied social and economic research in the OECD countries including Australia. This includes measuring income inequality at the regional level. In this article, we have used spatial microsimulation techniques to calculate small area inequality in Australia using disposable income data which are not available at a small area level, drawing together data from the Australian Census and survey data. Using disposable income data increases the strength of the results, as a more accurate measure of income distribution is able to be obtained. We estimate inequality at a small area level for the two most populous states in Australia – New South Wales and Victoria using conventional Gini coefficient methodology. We also examine the differences in inequality between the densely populated capital cities of each state and the balance of these states or rural areas. The results show that there are marked variations in inequality with distinct pockets of small areas with high income inequality in both states and their capital cities. The small area inequality estimation enables the policy maker to pinpoint pockets of inequality. This will be useful to identify regions that need better targeting/interventions.
1. Introduction
Measuring income inequality has long been of interest in applied social and economic research in the OECD countries including Australia. Inequality can have social and political implications as Wilkinson (2006) argues this may create social and political conflict, violence and other issues. Knowing inequality is important because it helps policy makers to understand better the causes of inequality and may help target policy programs better. In comparison to other OECD countries, the recent data in late 2000s, shows that Australia was the 9th most unequal of the 34 OECD members with a Gini coefficient of 0.34 (OECD 2011). This was substantially higher than Slovenia, which had the lowest inequality of 0.24, higher than the OECD average of 0.31, but much lower than Chile, which had the highest inequality of 0.49 (OECD 2011)1. Further, inequality in Australia has been increasing in the last decade, with the data showing the Gini coefficient was lower at 0.305 in early 2000s. While this provides us with a picture of where Australia falls internationally in terms of income inequality, much more can be said about the nature of inequality in Australia, and in this paper we focus on a sub-national analysis of Australia’s income inequality.
Previous Australian studies mostly consider Australian income inequality at a national level, with only a few authors studying this phenomenon at a regional level. However, as there is increasing interest in studying regional diversity in inequality, as discussed by Athanasopoulous and Vahid (2003), policy makers are now interested in examining income inequality within and between regions (Chotikapanich et al. 2005; Gregory & Hunter 1995; Lyold et al. 2000). Just as the fruits of the recent economic boom are not spread evenly across all regions in Australia (Meagher & Wilson 2008; Miranti et al. 2010; Saunders et al. 2008; Vu et al. 2008), it is likely that the average Gini we see nationally is in fact much higher (or lower) in some areas. There is some support for this notion in previous literature.
Internationally, there have been several studies that seek to measure inequality at broader geographic levels in order to analyze the regional disparities within a country. Trendle (2005) explains that the spatial variation of income inequality has been a debate within the field of regional science. Examples of this research includes Loikkanen et al. (2002) who examine inequality for Finland; Akita (2003) for China and Indonesia; Gray et al. (2003) for Canada; Balisacan and Fuwa (2006) for the Philippines and Elbers et al. (2005) for Ecuador. However, there are few international studies that have sought to measure inequality at smaller geographic levels. Among these studies, Elbers et al. (2003) and Tarozzi and Deaton (2009) have developed methods to calculate small area poverty and inequality in developing countries. Further, Ballas (2004) uses microsimulation to estimate the trends in poverty and inequality for two cities in England.
This research contributes to international research on small area inequality and expands the previous research in this field with two improvements. First, this research explores inequality for small areas using equivalised household disposable income data calculated using spatial microsimulation techniques, whilst for example, Athanasopoulos and Vahid (2003) use gross income. As disposable income data is not available at a small area level, a spatial microsimulation model is used to calculate inequality. Using equivalised household disposable income increases the strength of the results, as a more accurate measure of living standards is able to be obtained as it measures resources available to households after paying income tax (Lyold et al. 2000) and provides a truer measure of inequality: as argued in Harding (1997) there is some evidence that the income tax system has become more progressive and provides an offsetting force to growing inequality of gross income. Second, the unit of analysis used in this paper is the Statistical Local Area (SLA), which is a smaller geographical unit than any that has been used in previous Australian studies. Using a smaller spatial unit has several advantages, including the ability to pinpoint pockets of inequality, to link these with other small area characteristics, and to assist with effective policy and program targeting. An additional advantage of the methodology used in our analysis is that it gives a more precise measure of inequality than traditional measures, due to the ability of spatial microsimulation to create the distribution of disposable household income at the small area level.
We estimate inequality at a small area using conventional Gini coefficient methodology. We limit our analysis to two states – New South Wales (NSW) and Victoria, as the SLAs in these two states are relatively comparable in terms of population size, and therefore issues associated with different levels of heterogeneity in geographical units of different population sizes (known as the Modifiable Areal Unit Problem) are minimized. These states are also the two most populous states in Australia, containing around 58 percent of Australia’s total population in 2006. We calculate Gini coefficients for each SLA in New South Wales and Victoria. There are two main objectives of this research. Firstly, to provide valuable information about regional inequality at a small area level at a more disaggregated geographical level than what has been done previously. Secondly, to explore another use of spatial microsimulation and demonstrate its superiority in this area so that similar methodology can be applied to estimate small area inequality in other countries.
The remainder of this paper is organised as follows. The following section outlines the data, the methodology (spatial microsimulation and inequality measurement) and the validation used in this paper. The third section discusses the findings of the distribution of spatial inequality across the states of New South Wales and Victoria and interpretations of the results. Section Four finally provides a conclusion, lessons learned and policy implications.
2. Data, methodology and validation
2.1 Data
All data used in this study are originally sourced from the Australian Bureau of Statistics (ABS). All income data are sourced from the 2005–06 Survey of Income and Housing (SIH). For the spatial microsimulation analysis, the 2006 Census and the 2003–04 and 2005–06 ABS Surveys of Income and Housing are combined to maximize sample size. Validation is conducted using national, state, and small area level data published by the ABS, using the 2006 Census and the Confidentialised Unit Record Files (CURF) survey data (2005–06 SIH). A new model based on Census 2011 has not yet been constructed.
The 2003–04 SIH has a sample size of 11,361 households whilst the 2005–06 SIH has a sample size of 9,961 households. The sample used by the ABS for the SIH covers occupied private dwellings only. In contrast to the Census, the SIH has rich, detailed information about a range of socioeconomic variables, including disposable income. This detailed information on the SIH allows Gini coefficients to be generated using equivalised disposable income, in comparison to Census data which only provides income in ranges and available as gross income only.2 However, the SIH does not provide a detailed geographical disaggregation. Therefore, the SIH is suitable for analysing inequality at a larger geographical area such as national or state level, but not for small areas; while the Census is suitable for analysing many household characteristics at a small area level, but does not provide enough income data to create acceptable measures of inequality. Our spatial microsimulation techniques bring these two data sources together, using the Census to provide reliable small area benchmarks, creating household weights for each SLA, which are used to reweight the unit record file from SIH data. The Gini coefficients are calculated at the person level using household income, as we assume income sharing within households and, prior to conducting the analysis, negative household incomes are recoded to zero to follow the standard approach of the ABS (Li 2005). Li (2005) and Saunders et al. (2008) argue some analysis has shown that the expenditure patterns of those households with zero and negative incomes are inconsistent with their reported low income.
Disposable household income is chosen since this is a better measure for income distribution analysis as it measures resources available to households after paying income tax (Lyold et al. 2000) and as argued in Harding (1997) there is some evidence that the income tax system has become more progressive and provides an offsetting force to growing inequality of gross income. Income in Census data is only available as gross household income. In common with other research, disposable household incomes are equivalised, so that rankings of income will then take into account the differences that household size and composition make to standards of living. Equivalence scales give ‘points’ to each adult and child in the household, and then the household’s disposable income is divided by the sum of these points so that incomes can be compared across different types of households. Here we use the modified OECD equivalence scale, which assigns the following values: 1.0 point for the first adult; 0.5 for each of the remaining adults and 0.3 for each dependent child in the household. It should be noted that for the purposes of calculating equivalised income, dependent children are defined as only those children aged less than 15 years, in common with current Australian practice.
The spatial unit used in this paper is the Statistical Local Area (SLA). The SLA is one type of standard spatial unit described in the Australian Standard Geographic Classification (ASGC) 2006 and is based on the boundaries of incorporated local government bodies where these exist (ABS 2007a). The 2006 Census data covered 1,426 SLAs in Australia. There are 200 SLAs in New South Wales, 210 in Victoria, 479 in Queensland, 128 in South Australia, 156 in Western Australia, 44 in Tasmania, 96 in the Northern Territory, and 109 in the Australian Capital Territory.
There are two main reasons why the SLA is used as the unit of analysis in this study. First, the SLA is the smallest unit in the ASGC where there are not substantial issues with confidentiality. Second, SLAs cover the whole of Australia (as opposed to other spatial unit such as Local Government Areas which do not cover areas with no local government) and cover contiguous areas (unlike some postcodes).
2.2 Spatial microsimulation methodology
Spatial microsimulation is essentially the calculation of a set of small area weights. By combining detail available on data-rich surveys with detail available on the geographically rich Census, we are able to create synthetic data that accurately estimate certain socio-economic phenomena that are closely related to the benchmarks which work as a predictor or determinant in the estimation to calculate these weights.
A set of data that is directly comparable between the survey and Census data is selected, and adjusted into appropriate cross-tabulations and groupings. These tables are known as “benchmark” tables, and currently comprise the variables shown in Table 1. Tanton et al. (2013) has indicated that the choice of benchmarks needs to be correlated with the estimated variable of interest. Given that this particular study investigates inequality in terms of equivalised household disposable income, the spatial microsimulation estimates cannot solely depend on gross equivalised weekly household income data that are available in the Census data. The simulation also needs to include other variables that may affect tax paid and benefits received and consequently disposable income estimates. This means other household characteristics need to be included in addition to the income variable. As shown in Table 1, most of the benchmark tables are at household level, and only three are “person” level benchmarks.
Tenure, rent and mortgage structure need to be introduced not only because the Australian social welfare system includes rent assistance for eligible households, but also because the pension system has differentiated benefits for home owners and non-home owners (Centrelink 2015). The differentiated government benefits available to different household profiles are also the reason for introducing family composition as a benchmark indicator. Both the number of children and adults and the family type (e.g. single or couple households) will impact upon the amount of government benefits a household is eligible to receive. Moreover, the addition of information about the number of children and adults residing in a household will ensure that the equivalised scale is applied correctly.
Benchmark tables used for SpatialMSM
| N° | Benchmark table | Level |
|---|---|---|
| 1 | All household type | Household |
| 2 | Age by sex by labour force status | Person |
| 3 | Tenure by weekly household rent | Household |
| 4 | Tenure by household type | Household |
| 5 | Tenure by weekly household income | Household |
| 6 | Persons in non-private dwellings | Person |
| 7 | Monthly household mortgage by weekly household income | Household |
| 8 | Dwelling structure by household family composition | Household |
| 9 | Number of children aged under 15 usually resident in household | Household |
| 10 | Number of adults usually resident in household | Household |
| 11 | Weekly household rent by weekly household income | Household |
| 12 | Gross equivalised weekly household income by age | Person |
Both the survey data and the Census are adjusted and manipulated in order to gain alignment for use in the reweighting process. Income values are uprated on both surveys using average weekly earnings in order to coincide with 2006 dollar values and mortgages and rents are also uprated using a factor derived from the Consumer Price Index. Extensive work has been undertaken for all benchmark components to ensure that they have the same definition and coverage on both the Census and the SIH (see Cassells et al. 2013) for more detail).
The reweighting process is carried out for the whole of Australia and followed the methodology described in Chin and Harding (2006) and Cassells et al. (2013). The procedure used is a SAS macro called GREGWT which uses an iterative constrained optimization technique to calculate weights that best represent all the Census benchmarks. The procedure is a generalised regression procedure outlined in Bell (2000). Because the reweighting process is an iterative process, there are areas where the procedure does not find a solution. If there is no solution found after 30 iterations, then the process has not converged. Those SLAs where the process does not converge are usually SLAs where the population is quite different to the sample population – for example, industrial estates or inner city areas.
However, for some SLAs, it is found that the GREGWT criterion for non-convergence is too strict: even after iterating 30 times and not converging, the estimates obtained from the weights were still reasonable when compared with the benchmarks. Therefore, a new criterion for reweighting accuracy, which uses the total absolute error (TAE) from all benchmarks is calculated in order to maximize the number of SLAs for which we can produce valid data. With the latest criteria, if the absolute total error from all the benchmarks is greater than the population in that SLA, then the accuracy criteria has failed, and the SLA is dropped from any further analysis. Generally, the convergence criteria and the accuracy criteria provide the same results when an area has obviously not converged; but for marginal areas, the area may reach the maximum number of iterations but still provide a reasonable total absolute error. In the final results, TAE criteria are used rather than the GREGWT convergence criteria.
While the acceptance rate of SLAs is overall very high (especially when considered in population terms), we lose almost a third of the Northern Territory population in this reweighting process however as our research concentrates on New South Wales and Victoria, this does not affect our results.3 It should also be noted that validation of our Gini coefficient estimates results in the exclusion of some additional SLAs. Using the TAE criteria, only 2 SLAs are lost from NSW and 7 SLAs are lost from Victoria. This represents 0.34 per cent of the total NSW population and 0.52 per cent from Victoria, respectively (Table 2).
Number and characteristics of failed SLAs
| State/Territory | Total SLAs | Failed SLAs | Proportion of failed SLAs | Proportion of persons living in failed SLAs out of all persons within state/territory |
|---|---|---|---|---|
| New South Wales | 200 | 2 | 1.0% | 0.34% |
| Victoria | 210 | 7 | 3.3% | 0.52% |
| Queensland | 479 | 45 | 9.4% | 0.75% |
| South Australia | 128 | 7 | 5.5% | 0.32% |
| Western Australia | 156 | 17 | 10.9% | 0.87% |
| Tasmania | 44 | 2 | 4.5% | 0.15% |
| Northern Territory | 96 | 53 | 55.2% | 28.37% |
| Australian Capital Territory | 109 | 16 | 14.7% | 0.61% |
| AUSTRALIA | 1422 | 149 | 10.5% | 0.79% |
-
Source: SpatialMSM/09C applied to SIH2003–04 and SIH2005–06, ABS Census Population and Housing 2006.
One SLA is further excluded from the sample where the estimated population size is less than 30 persons, as this population size is considered to be too small to produce reliable estimates. In the end we use 197 SLAs from NSW and 198 SLAs from Victoria.
2.3 Inequality measurement methodology
There are various ways to measure inequality (see ABS 2006b) for a summary of measures of inequality including the Theil and Atkinson Index). This paper uses a Gini coefficient which measures disparity between each person in the population and every other person in the population through income. Gini coefficients are used to measure inequality for two reasons as follows: (i) the Gini coefficient is the most commonly used summary measure (Athanasopoulous and Vahid 2003; ABS 2006b); and (ii) Gini coefficients are the only statistical measure of income distribution (at the national and state level) published by the ABS and thus allow us to validate our spatially microsimulated small area Gini coefficient estimates.
The Gini coefficient can be calculated by examining the Lorenz curve. The Lorenz curve is a curve with the horizontal axis showing the cumulative proportion of the persons in the population ranked according to their income and with the vertical axis showing the corresponding cumulative proportion of equivalised disposable household income.
The Gini coefficient has a value between zero and one. A value of zero means perfect equality, a situation in which everyone in the population lives in a household with the same level of equivalised income. A value of one indicates perfect inequality, a situation where one person holds all the income. Smaller Gini coefficients indicate a more equal distribution of income.
In this paper, as explained earlier, the household weights generated from the spatial microsimulation model are applied to calculate Gini coefficients at a small area level for the whole of Australia. Therefore, the estimates of Gini coefficients are calculated using a weighted Gini formula as adapted in Harding and Greenwell (2001).
Applying household weights in each SLA to calculate Gini coefficients is challenging as there is no actual unit record data to calculate the Lorenz curve. Therefore, as highlighted in Harding and Greenwell (2001), the income distribution is determined by ranking people by their equivalised household income (based on the spatial microsimulation results). Consequently, we calculate the Gini, by applying the weights to the whole income record in the SIH data, so if a household has five people (as the weight), their equivalised income will be counted five times, not once.
2.4 Validation
As the estimates of the Gini coefficient are calculated using spatial microsimulation techniques, we undertook aggregate data validation in order to check the accuracy of our synthetic estimates.
The validation was conducted using aggregated equivalised disposable household income data from the 2005–06 SIH. Income collected from the survey is argued to provide more accurate estimates of the distribution of income than income collected from the Census as interviewers are involved in collecting data directly from the survey respondents, whereas for the Census, the respondents complete the Census questionnaires without an interviewer’s guidance (Maxwell & Peter 1988).
The Gini coefficients estimated at an SLA level were aggregated to the state and capital city and balance of state levels or rural areas in order to compare these results directly with results available at this geographic level from the SIH. Specifically, we summed the weights of each SLA in the region then apply this weight to the unit record file from the SIH.
Table 3 indicates that while the Gini coefficient estimates from spatial microsimulation tend to be higher than estimates from the 2005–06 SIH, the results are generally aligned. The slightly higher estimates from the spatial microsimulation are possibly due to benchmarking to Census data, which may have a greater amount of persons reporting lower incomes than the sample in the SIH, however overall the results are very promising. It was also found that the Gini coefficient estimates for the balance of each state have greater differences than those estimated for each capital city.
Comparison of Gini coefficient estimates from the 2005–06
Survey of Income and Housing and SpatialMSM
| State | Capital City/Balance of state | SpatialMSM/09C | 2005–06 SIH |
|---|---|---|---|
| New South Wales | All | 0.322 (+) | 0.317 |
| Sidney | 0.324(+) | 0.321 * | |
| Balance of state | 0.300(+) | 0.287 * | |
| Victoria | All | 0.306 | 0.306 |
| Melbourne | 0.308(−) | 0.309 * | |
| Balance of state | 0.290(+) | 0.274 * | |
| AUSTRALIA | 0.308(+) | 0.307 |
-
+(−)
indicates where the estimates from spatial microsimulation are higher or lower than the estimates directly from 2005–06 SIH;
-
*
Indicates that the coefficients have been calculated by authors. The Gini data at the capital city and balance of state level are not available from the ABS publication.
The aggregated data validation also shows that in general the capital cities have a higher Gini coefficient when compared to the rural areas. This finding confirms previous research (Bray 2001; Lloyd et al. 2000). This may reflect that the capital cities in Australia are more heterogeneous in terms of income than the rural areas, as cities have a predominance of upper-middle income households together with very low income households (Lloyd et al. 2000). However, our results also show that capital city estimates are closer to the estimates from the SIH than regional areas. Table 3 also shows that incomes in New South Wales are distributed relatively more unequally than incomes in Victoria.
3. Small area results
3.1 Spatial distribution of inequality
The following section will discuss geographic distribution of inequality in both NSW and Victoria, both in the capital cities and in the rural areas by focusing the patterns at a small area level.
Figure 1 shows the natural breaking of inequality for New South Wales SLAs. The 197 areas are ranked and then divided into five categories according to where the greatest differences are in the data. Similarly Figure 2 applies the same natural break categories for the whole of New South Wales to Sydney, the capital city of NSW. The palest colour on the map represents areas that have the lowest income inequality category (the lowest Gini coefficient) while, in contrast, the darkest colour on the map represents areas with the highest income inequality (the highest Gini coefficient). The missing data on maps represents the excluded SLAs due to inadequate estimates and population sizes, as discussed earlier. The Gini coefficients in New South Wales vary between 0.262 and 0.369.
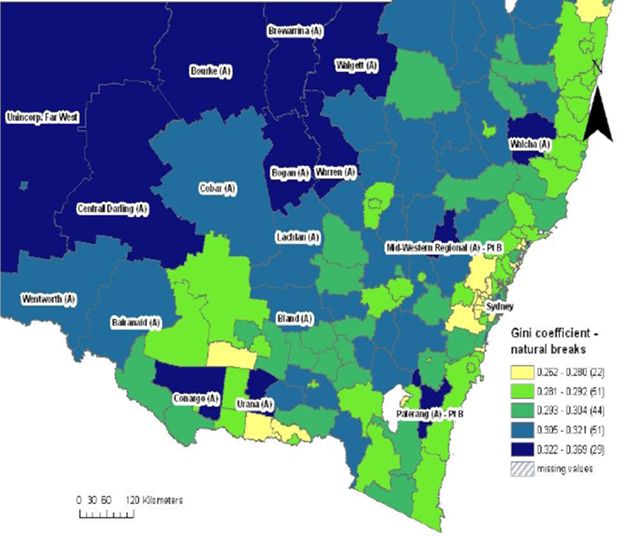
Gini coefficients by statistical local area, new south wales.
Source: SpatialMSM/09C applied to 2003–04 and 2005–06 SIH, ABS Census Population and Housing 2006.
Comparing Figures 1 and 2, over 50 per cent of SLAs in the highest income inequality category (29 SLAs) lie within the capital city – Sydney (16 SLAs). SLAs with high income inequality are mostly clustered in Sydney, with some additional high inequality SLAs scattered throughout the rural areas of NSW. In Sydney, these SLAs run in a horizontal corridor, from east to west, starting at the inner city suburbs of Waverley, Woollahra, Randwick, Ashfield and Strathfield, and flowing out along the western motorway (M4) and the major train line, towards the western suburbs of Auburn and Parramatta. For the rural areas of New South Wales, most SLAs with high inequality are concentrated in the remote far west and north western areas of New South Wales.
However, there are several small areas with high income inequality scattered throughout New South Wales, including Conargo, Urana, Palerang and Mid-Western Regional. Further, Newcastle, a major urban area, just north of Sydney (unable to be identified readily on the map) is also an SLA that falls within the highest income inequality grouping.
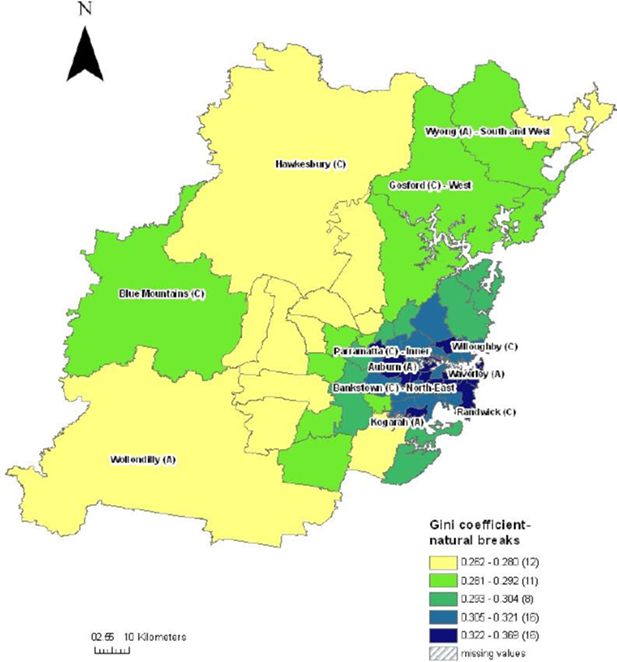
Gini coefficients by statistical local area, Sydney.
Source: SpatialMSM/09C applied to 2003–04 and 2005–06 SIH, ABS Census Population and Housing 2006.
Figures 3 and 4 show the spatial distribution of income inequality for Victoria and Melbourne, by applying the natural break classification for the whole of Victoria. Figure 3 shows the 198 Victorian SLAs divided into five categories and similarly for Melbourne, the capital city of Victoria (Figure 4), using the same categories. As with New South Wales, the palest colour on the map represents the areas with the lowest income inequality and the darkest colour, areas with the highest income inequality (the highest Gini coefficient).
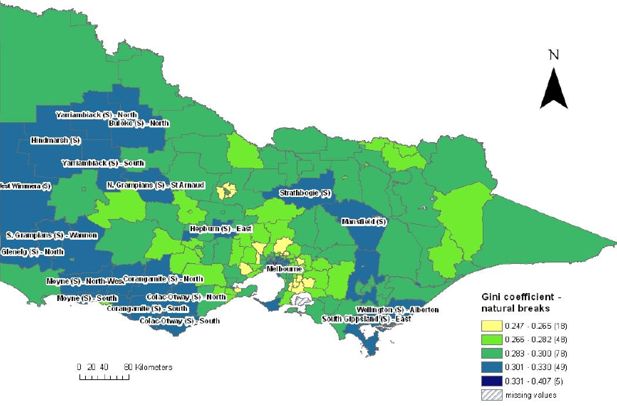
Gini coefficients by statistical local area, Victoria.
Source: SpatialMSM09C applied to 2003–04 and 2005–06 SIH, ABS census population and housing 2006.
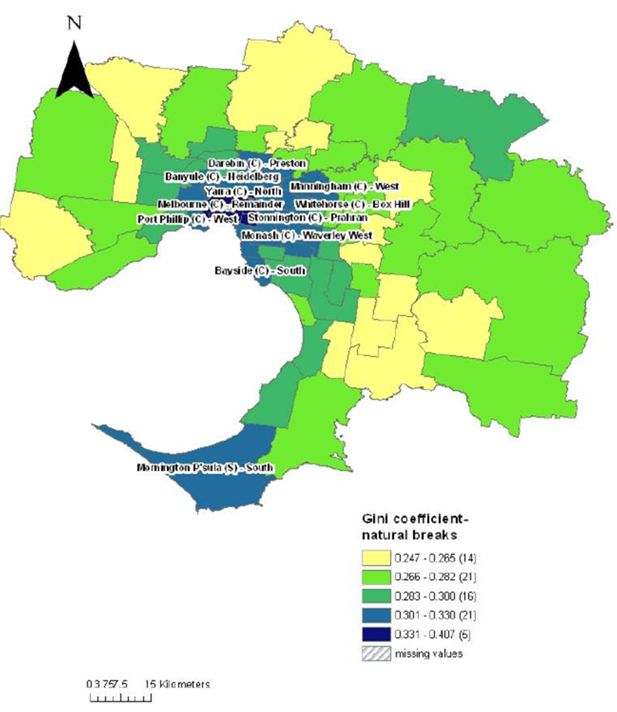
Gini coefficients by statistical local area, melbourne.
Source: SpatialMSM09C applied to 2003–04 and 2005–06 SIH, ABS Census Population and Housing 2006
Figure 4 shows that the Gini coefficients in Victoria vary between 0.247 and 0.407. Figure 4 also shows that there are only five SLAs in Victoria that fall within the highest category of inequality, and all of these SLAs lie within the Melbourne city statistical division. These SLAs are clustered in the inner city area of Melbourne and include the SLAs of Melbourne – Remainder, Port Phillips – West, Stonnington, Yarra – North and Yarra – Richmond. No SLAs in the rural areas of Victoria fall into the highest inequality category, however, from Figure 4, we can see that there is a large cluster of SLAs in the west of the state that fall into the second highest category of income inequality – for example, West Wimmera, Hindmarsh, Moyne, Yarriambiack, Grampians and Corangamite.
From these data it can be seen that in Victoria, all high inequality SLAs fall within the capital city – Melbourne, rather than the rural areas of Victoria. However for New South Wales, the high inequality SLAs are spread evenly between the rural areas and capital city of Sydney, with a little over 50 per cent of high inequality SLAs found in Sydney (although it should be noted again that the definition of ‘high inequality’ in these maps differs between the two states due to the differences in natural breaks).
3.2 Discussion
Our small area analysis shows that some areas in NSW and Victoria have been categorised as high inequality areas and some areas as low inequality areas. While these findings may be useful for the purpose of policy interventions, the results and their implications should be interpreted cautiously, due to the complexities inherent in understanding the phenomenon of high inequality in small areas. For example, small areas with low inequality may not necessarily reflect a more cohesive society overall or a lack of social and economic problems. A number of studies, especially those from United States have indicated that low inequality in small areas may also point towards segregation issues. Watson (2009) has argued that inequality may affect income sorting that leads to income segregation at the neighbourhood level. Reardon and Bischoff (2011) echo these results stating that lower income households tend to live in neighbourhoods with lower incomes while higher income households tend to live within neighbourhoods with higher incomes. Income segregation may have a negative impact on social, political and health related outcomes. Racial tensions and increasing crime rates are examples of these unwanted outcomes (Bayer et al. 2014; Sethi and Somathan, 2004; Watson 2009). Thus, policy makers need to consider the balance between the potential benefits of reducing within-area inequality and the potential adverse impact of segregation, particularly where this has implications for high levels of neighbourhood or interregional inequality. However, it is not clear to what extent international findings are relevant in an Australian context, and research has found more inequality between neighbourhoods in the United States than in Australia (Hunter 2003).
In considering the characteristics associated with inequality, previous research has uncovered factors that have been found to be determinants of inequality in Australia (see for example Maxwell and Peter 1988; McGillivray and Peter 1991; Trendle 2005). These factors include variables that are often associated with low income, including immigration status (Greig et al. 2003; McGillivray and Peter 1991), Indigenous status (Trendle 2005) and public housing tenancy; as well as those that are closely related with high income, such as those with ‘high-end’ occupations, working as professionals or managers (Lyold et al. 2000) or those who have higher educational attainment (Glaeser, et al. 2008; Maxwell and Peter 1988; Trendle 2005). McGillivray and Peter (1991) and Trendle (2005) also examined the association between female labour force participation and inequality. However, previous literature has shown that the relationship of many of these variables to regional inequality is often ambiguous.
Table 4 shows the average proportion of persons in each Gini coefficient group by selected characteristics for all of New South Wales. The groups are selected based on the natural breaks which were applied on the maps. From Table 4 it can be seen that SLAs in the highest inequality group are characterised by, on average, high proportions of immigrants or Culturally and Linguistically Diverse (CALD) communities, Indigenous persons, people working as managers and professionals, female labour force participation, people having a bachelor degree or higher, and people living in public housing (in comparison to other Gini coefficient groups).
Average proportion of persons in each Gini coefficient group by selected characteristics, all New South Wales, 2006.
In %
| Gini coefficient – natural breaks* | Immigrants | Indigenous | Managers and professionals | Female LFPR | Bachelor + | Public Housing |
|---|---|---|---|---|---|---|
| 1 lowest inequality | 16.37 | 2.61 | 28.56 | 56.25 | 21.43 | 3.42 |
| 2 | 12.21 | 3.27 | 30.59 | 51.28 | 20.27 | 3.94 |
| 3 | 12.73 | 3.06 | 33.97 | 51.12 | 22.13 | 3.54 |
| 4 | 15.53 | 4.62 | 39.70 | 52.04 | 25.55 | 3.33 |
| 5 highest inequality | 23.79 | 7.19 | 46.17 | 54.59 | 33.46 | 4.51 |
-
Source: ABS Census Population and Housing 2006.
Table 5 shows similar results for Victoria. In general, SLAs which fall into the highest inequality group in Victoria, except for the proportion of population who are Indigenous (no clear pattern), show the same pattern as in New South Wales and have high average proportions of immigrants, people working as managers and professionals, female labour force participation, persons with a bachelor degree or higher, and persons living in public housing.
It is interesting that the lowest inequality group in New South Wales and Victoria also has high proportions of CALD, and high female labour force participation. This suggests that the relationships between these variables and inequality are complex and future research is warranted.
Average proportion of persons in each Gini coefficient group by selected characteristics, all Victoria, 2006.
In %
| Gini coefficient – natural breaks* | Immigrants | Indigenous | Managers and professionals | Female LFPR | Bachelor + | Public Housing |
|---|---|---|---|---|---|---|
| 1 lowest inequality | 17.98 | 0.56 | 25.48 | 59.97 | 22.09 | 1.57 |
| 2 | 14.29 | 0.71 | 30.11 | 55.43 | 23.71 | 2.47 |
| 3 | 14.13 | 1.07 | 33.41 | 51.41 | 21.96 | 2.55 |
| 4 | 16.99 | 0.53 | 44.22 | 53.17 | 32.62 | 2.08 |
| 5 highest inequality | 30.18 | 0.31 | 56.23 | 60.79 | 54.69 | 9.69 |
-
Source: ABS Census Population and Housing 2006.
4. Conclusion, lessons learned and policy implications
This research has demonstrated that spatial microsimulation is an effective analytical tool that can be used to enhance estimates of inequality at small geographic levels. The validation process shows that our results are robust, and are closely aligned with the aggregate direct estimates calculated from the 2005–06 Survey of Income and Housing.
The results show that although there are slight differences in terms of magnitude, the weights give reasonable results for the vast majority of small areas in these two states, with the broad regional rankings being very similar across both the Census and the synthetic estimates.
Our research has shown that there are clear groupings of small areas with high income inequality in Sydney, Melbourne and rural areas of New South Wales, but not in the rural areas of Victoria. There are several key lessons learned from this analysis of small area inequality. Firstly, the paper has demonstrated the use of a spatial microsimulation technique to estimate inequality at small area level that can be applied in other countries. Secondly, the findings of this research show that inequality does differ considerably when drilling down to smaller spatial areas. For example, we have found that most of small areas with the highest income inequality are clustered in the capital cities but not necessarily in the rural areas.
These key lessons are important, as they can assist to inform regional policy aimed at reducing inequality. By knowing which small areas are more unequal in regards to income, together with the characteristics of these areas, policy makers and service providers are able to better understand the intricacies of inequality and identify possible drivers, which can aid in more efficient targeting of programs and policy. Nevertheless, it is important to note that examining small area inequality does not in and of itself lead to definitive conclusions about the overall wellbeing of an area. In particular, low inequality does not necessarily equate to better community outcomes, nor does high inequality necessarily relate to poorer outcomes. Low inequality within an area may be a symptom of a highly segregated population, which in turn can be associated with interregional inequality and social unrest.
Future work in this area will concentrate on the determinants of regional inequality in order to examine the variation of inequality across small areas in more depth, including taking into account the spatial autocorrelation that exists between small areas. The literature suggests that the relationships between the determinants of inequality are complex and often ambiguous. Other planned work includes applying an inequality decomposition technique to separate ‘between’ and ‘within’ regional inequality and to apply the spatial microsimulation technique further in order to model policy changes in terms of examining the impact of income distribution policies on inequality at a small area level.
Footnotes
1.
Gini coefficients are calculated for persons using household disposable income.
2.
There is a large literature on the estimation of Gini coefficients from grouped data. See for example Kakwani and Podder (1973) and Wodon and Yitzhaki (2003).
3.
Only 0.79 per cent of the total Australian population in 2006 are lost in the reweighting process.
References
-
1
Income and Housing Survey (2005–06)Income and Housing Survey (2005–06), 2, Basic Confidentialised Unit Record Files.
-
2
Household Expenditure Survey and Survey of Income and Housing: User Guide (2003–04). Cat no. 6503.0Household Expenditure Survey and Survey of Income and Housing: User Guide (2003–04). Cat no. 6503.0.
-
3
Australian Standard Geographical Classification (ASGC). Cat. no. 1216.0Australian Standard Geographical Classification (ASGC). Cat. no. 1216.0.
-
4
Household Income and Income Distribution. Cat no. 6523.0Household Income and Income Distribution. Cat no. 6523.0.
- 5
-
6
Decomposing regional income inequality in China and Indonesia using two-stage nested Theil decomposition methodThe Annals of Regional Science 37:55–77.
-
7
Statistical Inference and Changes in Income Inequality in AustraliaThe Economic Record 79:412–24.
-
8
Simulating Trends in Poverty and Income Inequality on the Basis of 1991 and 2001 Census Data: a Tale of Two CitiesArea 36:146–63.
-
9
Changes in spatial income inequality in Philippines: An exploratory analysisIn: R Kanbur, AJ Venables, GH Wan, editors. Spatial Disparities in Human Development: Perspective from Asia. Tokyo: University Press United Nations. pp. 207–32.
-
10
Separate when equal? Racial inequality and residential segregationJournal of Urban Economics 82:32–48.
-
11
GREGWT and TABLE Macros – Users GuideCanberra: Unpublished Australian Bureau of Statistics.
-
12
Social Indicators for Regional Australia, Department of Families Housing Community Services and Indigenous Affairs Policy Research Paper No. 8Social Indicators for Regional Australia, Department of Families Housing Community Services and Indigenous Affairs Policy Research Paper No. 8.
-
13
Building a static spatial microsimulation model: data preparationIn: R. Tanton, K Edwards, editors. Spatial Microsimulation: A Reference Guide for Users. UK: Springer. pp. 9–16.
- 14
-
15
Regional Dimensions: Creating Synthetic Small-area Micro Data and Spatial Microsimulation Models. NATSEM Technical Paper No. 33Regional Dimensions: Creating Synthetic Small-area Micro Data and Spatial Microsimulation Models. NATSEM Technical Paper No. 33.
-
16
Trends in Income Inequality and Poverty in Australia in the 1990s: Regional PerspectivesPaper presented at the Australian Social Policy Conference Sydney.
- 17
-
18
Are neighbours equal? Estimating local inequality in three developing countriesIn: R. Kanbur, AJ Venables, editors. Spatial Inequality and Development. Oxford: Oxford University Press. pp. 37–60.
-
19
Urban Inequality. NBER Working Paper No. 14419Urban Inequality. NBER Working Paper No. 14419.
-
20
New Perspective on Canadian National and Provincial Income InequalityPaper presented at the UNU-WIDER Conference on Inequality Poverty and Human Well-being Helsinki.
- 21
-
22
The Macro Economy and the Growth of Ghettos and Urban Poverty in Australia. Centre for Policy Research Discussion Paper No. 325The Macro Economy and the Growth of Ghettos and Urban Poverty in Australia. Centre for Policy Research Discussion Paper No. 325.
-
23
The Suffering Middle: Trends in Income Inequality in Australia. NATSEM Discussion Paper No. 21The Suffering Middle: Trends in Income Inequality in Australia. NATSEM Discussion Paper No. 21.
-
24
Trends in Income and Expenditure Inequality in the 1980s and 1990sPaper presented at the 30th Annual Conference of Economists.
-
25
Trends in Neighbourhood Inequality of AustralianAustralian Economic History Review 43:22–44.
-
26
On the estimation of Lorenz curves from grouped observationsInternational Economic Review 14:278–292.
-
27
Impact of Demographic and Economic Changes on Measured Income InequalityPaper presented at the Australian Social Policy Conference.
-
28
Regional Divide? A Study of Incomes in Regional AustraliaAustralasian Journal of Regional Studies 6:271–92.
-
29
Regional income convergence and inequality in boom and bust: results from micro data in Finland 1971&3x2013;1998 and especially during the 1990sPaper presented at the meeting of the ESRC Urban and Regional Economics Seminar Group University of Central Lancashire UK.
-
30
Income Inequality in Small Regions: A Study of Australian Statistical DivisionThe Review of Regional Studies 18:19–27.
-
31
Regional Income Inequality in A Developed Nation: A Cross-Sectional Study of Australian Sub-State RegionsThe Review of Regional Studies 21:137–51.
-
32
Richer but More Unequal: Perceptions of Inequality in Australia 1987–2005Journal of Australian Political Economy 61:220–43.
-
33
Children with Jobless Parents: National and Small Area Trends for Australia in the Past DecadeAustralian Journal of Labour Economics 13:27–48.
-
34
OECD Factbook 2011: Economic Environmental and Social StatisticsOECD Factbook 2011: Economic Environmental and Social Statistics, ISBN 978-92-6411150-9.
-
35
data extracted onhttp://www.oecd-ilibrary.org/statistics, data extracted on, 29, April.
-
36
Income Disparities and Population Movements in VictoriaThe Australasian Journal of Regional Studies 5:87–100.
-
37
Income inequality and income segregation1American Journal of Sociology 116:1092–1153.
-
38
Poverty in Australia: Sensitivity Analysis and Recent Trends. Social Policy Research Centre Report No. 4Poverty in Australia: Sensitivity Analysis and Recent Trends. Social Policy Research Centre Report No. 4.
- 39
- 40
-
41
Spatial Microsimulation Using a Generalised Regression ModelIn: R Tanton, K.L Edwards, editors. Spatial Microsimulation: A Reference Guide for Users. Netherlands: Springer. pp. 87–103.
-
42
Using Census and Survey Data to Estimate Poverty and Inequality for Small AreasThe Review of Economics and Statistics 91:773–92.
-
43
Sources of Regional Income Inequality: An Examination of Small Regions in QueenslandReview of Urban and Regional Development Studies 17:35–50.
-
44
On the risk of unemployment: A comparative Assessment of the Labour Market Success of Migrants in AustraliaAustralian Journal of Labour Economics 7:199–229.
-
45
Advance Australia Fair? AMP. NATSEM Income and Wealth Report, No. 20Advance Australia Fair? AMP. NATSEM Income and Wealth Report, No. 20.
-
46
Inequality and the measurement of residential segregation by income in American neighborhoodsReview of Income and Wealth 55:820–844.
-
47
The effect of using grouped data on the estimation of the Gini income elasticityEconomics Letters 78:153–159.
-
48
Regional Inequality and the Process of National DevelopmentEconomic Development and Cultural Change 13:3–47.
- 49
Article and author information
Author details
Acknowledgements
This paper was funded by an Australian Research Council Discovery Grant DP664429. The authors would like to thank the Chief Investigators on this grant, Professor Fiona Stanley, Professor Hal Kendig, Professor Bob Stimson, Professor Ann Harding, Professor Robert Tanton and Dr Sharon Goldfeld, as well as the Australian Bureau of Statistics for their inputs to the broader projects under this grant.
Publication history
- Version of Record published: August 31, 2015 (version 1)
Copyright
© 2015, Miranti et al.
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

