Cash transfer policies, taxation and the fall in inequality in Brazil an integrated microsimulation-CGE analysis

It is widely known that Brazil has one of the most unequal income distributions in the world, with a Gini index around 0.60 until the beginning of this century.¹ This high income inequality has been one of the main causes of the country’s equally high levels of poverty, despite often strong economic growth.

However, from 2001 to 2014, there was an unprecedented and continuous fall in income inequality, with the Gini index declining 13.5% from 0.594 to 0.513². This has coincided with a significant reduction of poverty. Between 2001 and 2014, the percentage of poor declined from 38.7% to 15.3%, while the percentage of extremely poor declined from 17.4% to 4.6%.³ These evolutions coincided with the introduction and expansion of targeted income transfer programs as part of a national poverty alleviation strategy.

There are many kinds of income transfer programs in Brazil, such as Programa Bolsa Família (PBF), Benefício de Prestação Continuada (BPC)⁴ and several retirement benefits and pensions. This research analyzes the first two programs (PBF and BPC) because they are the main cash transfer programs specifically designed as social policies with the purpose of poverty (and inequality) reduction.

PBF was created in October 2003 and is presently the federal government’s main cash transfer program. It is a cash transfer program with conditions such as 85% school attendance for children in schooling age, vaccination for children under six years old, and regular visits to a health center for both pregnant and breastfeeding women. In 2005, PBF had a total of 10.6 million beneficiary households and R$6.9 billion worth of transfers (equivalent to 0.3% of GDP in 2005).

BPC is a social assistance benefit since 1996. It aims to aid the elderly who are not included in the public social security system and the disabled who cannot support themselves despite their households’ financial care. Both beneficiary groups comprise 2.8 million beneficiaries, with a budget of R$9.7 billion (or 0.4% of GDP) for BPC in 2005. The benefit consists of a cash transfer amounting to one minimum wage (R$300 in 2005) where the beneficiary’s family per capita income must be less than a quarter of the minimum wage.

These programs aim to reduce poverty and income inequality, hence the need for evaluations of their effects. The most common approach is partial equilibrium and decomposition analysis. Hoffmann (2006b) points out that 31% of the decline in Brazil’s inequality – 87% in the country’s Northeast region – from 2002 to 2004 were due to the above mentioned programs. Barros et al. (2007c) estimated that PBF and BPC induced, respectively, around 11.8% and 11.1% of the fall in income inequality from 2001 to 2005. According to IPEA (2012), during the period from 2001 to 2011, these two programs contributed to reduce inequality by 17% (and up to 24% between 2003 and 2005).

The contribution of PBF and BPC is more impressive if one takes into account the limited budget of these public policies. In 2013, the total budget of the public social security system represented 10.9% of GDP (6.8% for the general system – INSS, and 4.1% for former public workers) while PBF and BPC represented only 0.5% and 0.65%, approximately.⁵

However, these partial equilibrium or decomposition approaches do not take into account systemic (general equilibrium) effects induced by these programs on the economy, as well as the feedback impacts to household income and consumer prices. When poor households receive transfers, they tend to consume more, which stimulates production and employment, and so on through a multiplier effect. These demand effects are enhanced when we take into account differences in the expenditure patterns of Brazilian households by income level. Among poor urban Brazilian households, food expenditure is 40% of total consumption, compared to only 12% for the richest households (Cury et al., 2006).

In addition, the relevance of the general equilibrium effects is justified by the size and evolution of the transfer programs. Almost 14 million households (around 20% of all households) are PBF beneficiaries, covering more than 50 million individuals (around 25% of the population). In 2014, the total value of cash transfers was R$27.2 billion, representing more than 0.5% of the Brazilian GDP.

In addition, we may expect that program effects are sensitive to the mechanism chosen to finance this specific public expenditure, which generate direct and general equilibrium effects of their own. Also, during 2003–2005 some important changes were introduced in the fiscal system. For example, in the social security budget, the sharpest revenue increase came from PIS-COFINS taxes (a rise of 30% in their GDP ratio), which in 2003–2004 started to levy imports.

Additionally, cash transfers may cause some beneficiaries to reduce labor supply. This may counteract some of the benefits of these programs. Recently, several studies aimed to estimate the effects of the PBF and other conditional cash transfer programs on adult labor supply in Brazil (e.g., Soares et al., 2007; Ferro and Nicollela, 2007; Teixeira, 2008; Covre et al., 2008; and Foguel and Barros, 2008). These studies use different empirical strategies to compare beneficiaries against comparable non-beneficiaries.

There is some evidence that PBF can reduce labor market participation mainly among beneficiary mothers. For example, Tavares (2008) found evidence of an adverse effect of PBF on beneficiary mothers’ willingness to participate in the labor market due, mainly, to the program’s conditionalities (education and health of children). On the other hand, Firpo et al. (2014) find evidence that some individuals (particularly women) deliberately reduce their labor income in order to qualify for the PBF. Similarly, Santos (2013) shows that the PBF has encouraged adult beneficiaries to offer informal labor. In both cases, the purpose of the beneficiary is hiding the real family income to continue receiving the cash grant.

Proving that a specific methodology is unequivocally superior to others is not an easy task. However, according to Cockburn et al. (2015), the analysis of the impacts of large-scale policies on income distribution requires the usage of tool that integrates microsimulation (MS) techniques and a computable general equilibrium (CGE) model. Given the systemic consequences of the PBF and BPC programs and their financing mechanisms on the overall economy, we adopt a CGE model integrated with a Microsimulation model (CGE-MS model) approach to evaluate the impacts of these programs on poverty and inequality in Brazil.

This paper is organized into five sections, including this introduction. The next section describes the methodology: the CGE model, the MS model, and their integration. The research questions, simulation scenarios and results are presented in Section 3. The last section presents the conclusion and the final remarks.⁶

This study applies a CGE-MS combined iterative approach, where the starting model (i.e. where the first shock is applied) is the MS model. For this reason, this kind of approach is referred to as bottom-up/top-down in the literature (see Cockburn et al., 2015, for a discussion of the various CGE-MS approaches).

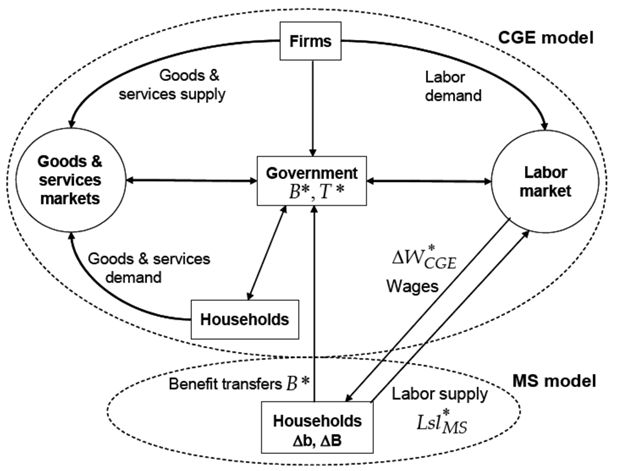
2.3 Integration of the CGE and MS models

The impacts of the PBF and BPC programs on welfare indicators are assessed with an integrated CGE-MS modeling framework with a bi-directional linkage to guarantee convergence of solutions for both models. The following illustrates how this bi-directional procedure:

Step 1

The MS model contains data on thousands of individuals, estimates the reservation wage $\begin{array}{l}\\ ({\overline{\omega }}_i^j)\end{array}$ for each person i in the database, and defines occupational levels for each category of private labor by means of the equations (4) and (5), as mentioned in Section 2.2.

First, for each simulation, the benefits received from the income transfer programs in 2003 (B_i) are replaced by their new values $(B_i^{*})$ in equations (4) and (5), whose re-estimation generate the Heckman post-simulation occupational level for each private labor type $(HLs{l}_{MS}^{*})$. Then, the difference between the Heckman post and pre-simulation occupational levels by private labor type, $(HLs{l}_{MS}^{*}-HLsl)$,¹⁹ are added to the original occupational level in the database (Lsl) , generating a post-simulation occupational level by private labor type calculated by the MS model $(Ls{l}_{MS}^{*})$.

Step 2

The occupational levels compatible with the new values of benefits $(Ls{l}_{MS}^{*})$, as well as the new amount of given benefits (B^*) , are then applied to the CGE model, where

(7) $B^{*}={\displaystyle \sum _i{\displaystyle \sum _i{B}_i^t},i=1,\mathrm{...},n;t=BF,BPC}$

and $B_i^t$ is the amount of benefits that individual i received from PBF and BPC.

The new values of taxes used to finance the changes in transfer programs (B^*) are also applied to the CGE model to simulate the changes they induce in the economic environment.

All these changes induce the economic system to achieve a new general equilibrium and, as part of this process, the labor market reach equilibrium with new real wage values $\left(W_{CGE}^{*}\right)$ for each kind of private labor.

Step 3

The percentage change in the average real wage $(\Delta W_{CGE}^{*})$ for each kind of private labor from the CGE simulation is applied to the wages earned by each person i in the MS model database (w_i), defining after-shock values for earned wages $(w_i^{*})$.²⁰ After this, we compare these new individual wages $w_i^{*}$ with their respective reservation wage $({\overline{w}}_i^j)$ by means of the Heckman procedure. Using the previously mentioned criterion for this procedure, we have that:

(8) $\{{}_{\text{otherwise,}\text{individual}i\text{is}\text{employed}.}^{\text{if}{w}_i^{*}<{\overline{w}}_i^j,\text{individual}i\text{is}\text{unemployed},}$

After classifying the workers by their reservation wages, those with the highest reservation wage are the first to become unemployed if the real wage decreases. However, if the real wage rises, the first to be employed will be those with the lowest reservation wage. Adding the number of people to be employed or unemployed according to this criterion to the initial occupational level defines a new occupational level for each private labor type $(Ls{l}_{MS}^{*})$.

Step 4

These new occupational levels are then transmitted to the CGE model as shown in Figure 1:

Figure 1

Download asset Open asset

If the occupational levels calculated by the MS model are different from those in the CGE model, they change the equilibrium of the labor markets, which will then change wages and the economic environment as a whole until the CGE model reaches a new equilibrium. In this sense, step 2 restarts, but without changes in benefits and their financing sources, and this integrated solution procedure loops until the differences in the occupational level for all private labor types calculated by the MS model (Lsl*) approaches zero.²¹

This association is done consistently with the equilibrium of aggregate markets in the CGE model, which requires that: (i) relative changes in average earnings in the MS model must be equal to changes in wage rates from the CGE model for each private wage group in the labor market; (ii) relative changes in the number of privately waged workers by labor market segment in the MS model must match those in the CGE model; and (iii) changes in the consumption price vector, p, must be consistent with the CGE.²²

According to the above procedure, the private labor supply is being modified with each simulation iteration; for example, some individuals will be losing their former jobs. If this happens, the share of each household in the total income of each labor category can also change (parameter ε_hl in equation 2.1.2). In order to capture these variations, we incorporate the differences among the parameter ε_hl, along the simulation rounds as a shock in the CGE as well, which performs simultaneously with the procedures described in this section.²³

The aim of the simulations presented here was to investigate the role of the two most important Brazilian cash transfer programs in reducing inequality. This was done through a CGE-microsimulation (CGE-MS) iterative approach. Two simulations were run, where the cost of increased transfers was financed by increased taxes or a rise in the public deficit.

The macro results showed that, in general, the impacts were adverse for several macro indicators, including GDP, employment, and price index. However, importantly, the study’s CGE-MS framework brings out the fact that the adverse results came mainly from the tax increases and not the increase in transfers.

The results confirmed the important role of the PBF and BPC programs in the recent reduction in income inequality in Brazil. Practically 20% of the fall in inequality between 2003 and 2005 can be attributed to the adopted policies. These results are similar to those reported by other studies using partial equilibrium/decomposition analysis. However, again, this study’s CGE-MS framework reveals that the accompanying tax reform played a major role in this process.

The programs also contributed to a reduction in poverty. However, the impacts were smaller than for inequality. The transfers generated positive impacts, but the general equilibrium effects of the changes in taxation to finance the program largely offset the former effect, particularly in the case of extreme poverty indicators. Household income was effected through reduction in labor and non-labor income.

In general, the results also demonstrated that the two analyzed programs have achieved their objective of reducing poverty and inequality. However, the simulations showed that PBF targeted its beneficiaries better, concentrating its benefits on poor households.

Finally, it is clear that the financing of transfer programs plays an important role in the final welfare impacts. In our opinion, this issue deserves more attention in a policy research agenda.

1. 1
   Income distribution policy in developing country: A case study of Korea

   1. I Adelman
   2. S Robinson

   (1978)

   Stanford CA: Stanford University Press.

   • Google Scholar
2. 2
   mimeo

   1. PR Agénor
   2. A Izquierdo
   3. H Fofack

   (2001)

   IMMPA: A Quantitative Macroeconomic Framework for the Analysis of Poverty Reduction Strategies, Washington, D.C., The World Bank, mimeo.

   • Google Scholar
3. 3
   ‘A Theory of Demand for Products Distinguished by Place of Production’. IMF Staff Papers

   1. P Armington

   (1969)

   157–178, ‘A Theory of Demand for Products Distinguished by Place of Production’. IMF Staff Papers, 16.

   • Google Scholar
4. 4
   Desigualdade de Renda no Brasil: uma análise da queda recente

   1. RP de Barros
   2. M Carvalho
   3. S Franco
   4. R Mendonça

   (2007)

   A Queda Recente da Desigualdade de Renda no Brasil, Desigualdade de Renda no Brasil: uma análise da queda recente, Brasília, Ipea, 1.

   • Google Scholar
5. 5
   Desigualdade de Renda no Brasil: uma análise da queda recente

   1. RP de Barros
   2. M Carvalho
   3. S Franco
   4. R Mendonça

   (2007)

   A importância da queda recente da desigualdade para a Pobreza, Desigualdade de Renda no Brasil: uma análise da queda recente, Brasília, Ipea, 1.

   • Google Scholar
6. 6
   Desigualdade de Renda no Brasil: uma análise da queda recente

   1. RP de Barros
   2. M Carvalho
   3. S Franco

   (2007)

   O papel das transferências públicas na queda recente da desigualdade de renda brasileira, Desigualdade de Renda no Brasil: uma análise da queda recente, Brasília, Ipea, 2.

   • Google Scholar
7. 7
   Pesquisa e Planejamento Econômico

   1. RP de Barros
   2. CH Corseuil
   3. S Cury

   (2000)

   157–182, Salário mínimo e pobreza: uma abordagem de equilíbrio geral, Pesquisa e Planejamento Econômico, Rio de Janeiro, IPEA, 30, 2.

   • Google Scholar
8. 8
   Desigualdade de Renda no Brasil: uma análise da queda recente

   1. RP de Barros
   2. MN Foguel
   3. G Ulyssea

   (2007d)

   Brasília: Ipea.

   • Google Scholar
9. 9
   ‘A Theory of Allocation of Time’

   1. GS Becker

   (1965)

   Economic Journal 75:493–517.

   • Google Scholar
10. 10
    ‘The wage curve’

    1. DG Blanchflower
    2. AJ Oswald

    (1990)

    Scandinavian Journal of Economics 92:215–235.

    • Google Scholar
11. 11
    The wage curve

    1. DG Blanchflower
    2. AJ Oswald

    (1994)

    Cambridge, Massachussetts: MIT Press.

    • Google Scholar
12. 12
    A labour supply: a review of alternative approaches

    1. R Blundell
    2. T McCurdy

    (1999)

    In: O Ashenfelter, D Card, editors. Handbook of Labor Economics III. Amsterdam: North Holland. pp. 1559–1695.

    • Google Scholar
13. 13
    Un modèle CGE-Multi-Ménages Intégrés Appliqué à l’Économie Sénégalaise

    1. D Boccanfuso
    2. F Cisse
    3. A Diagne
    4. L Savard

    (2003)

    mimeo: CREA, Dakar.

    • Google Scholar
14. 14
    Microsimulation Modelling for Policy Analysis: Challenges and Innovations

    1. C Bonnet
    2. R Mahieu

    (2000)

    Public pensions in a dynamic microanalytic framework: the case of France, Microsimulation Modelling for Policy Analysis: Challenges and Innovations, Cambridge University Press, Cambridge.

    • Google Scholar
15. 15
    ‘Representative versus Real Households in the Macroeconomic Modeling of Inequality’. Working Paper

    1. F Bourguignon
    2. AS Robilliard
    3. S Robinson

    (2003)

    ‘Representative versus Real Households in the Macroeconomic Modeling of Inequality’. Working Paper, nº. 2003-05, DELTA/ENS, Paris.

    • Google Scholar
16. 16
    The Impact of Macroeconomic Policies on Poverty and Income Distribution: Macro-Micro Evaluation Techniques and Tools

    1. F Bourguignon
    2. L Savard

    (2008)

    A CGE Integrated Multi-Household Model with Segmented Labour Markets and unemployment, The Impact of Macroeconomic Policies on Poverty and Income Distribution: Macro-Micro Evaluation Techniques and Tools, Palgrave-Macmillan Publishers Limited, Houndmills, England.

    • Google Scholar
17. 17
    ‘Welfare impacts of China’s accession to the world trade organization’

    1. S Chen
    2. M Ravallion

    (2004)

    The World Bank Economic Review 18:29–57.

    • Google Scholar
18. 18
    ‘Poverty-Reduction Targeting Programs: a General Equilibrium Approach’

    1. NC Chia
    2. S Wahba
    3. J Whalley

    (1994)

    Journal of African Economies 3:309–338.

    • Google Scholar
19. 19
    Evaluating Targeted Cash Transfer Programs – A General Equilibrium Framework with an Application to Mexico. Research Report 137

    1. DP Coady
    2. RL Harris

    (2004)

    Washington, DC: International Food Policy Research Institute.

    • Google Scholar
20. 20
    ‘Trade liberalization and Poverty in Nepal: A Computable General Equilibrium micro-simulation Analysis’. Working paper

    1. J Cockburn

    (2001)

    ‘Trade liberalization and Poverty in Nepal: A Computable General Equilibrium micro-simulation Analysis’. Working paper, nº. 01-18, CREFA, Université Laval.

    • Google Scholar
21. 21
    The Handbook of Microsimulation Modelling

    1. J Cockburn
    2. L Savard
    3. L Tiberti

    (2015)

    Macro-Micro Models, The Handbook of Microsimulation Modelling, Emerald Group Publishing Limited.

    • Google Scholar
22. 22
    Um modelo de equilíbrio geral computável para analisar aspectos distributivos no Brasil

    1. AM Coelho
    2. CH Corseuil
    3. S Cury
    4. RP de Barros

    (2003)

    In: CH Corseuil, H Kume, editors. A Abertura Comercial Brasileira nos anos 90 – impactos sobre emprego e salário. Rio de Janeiro: IPEA. pp. 171–197.

    • Google Scholar
23. 23
    ‘Poverty and Policy: Some experiments with a SAM-Based CGE Model for Ghana’

    1. D Colatei
    2. JI Round

    (2001)

    Paper presented to the XIII International Conference on Input-Output Techniques.

    • Google Scholar
24. 24
    ‘Oferta de trabalho e transferências: Evidências dos efeitos das condições impostas pelo programa Bolsa-Família’

    1. S Covre
    2. F Marques
    3. E Mattos

    (2008)
25. 25
    PhD dissertation (Doutorado em Economia de Empresas) – Depto de Economia, Escola de Administração de Empresas de São Paulo

    1. S Cury

    (1998)

    Modelo de equilíbrio geral para simulação de políticas de distribuição de renda e crescimento no Brasil, PhD dissertation (Doutorado em Economia de Empresas) – Depto de Economia, Escola de Administração de Empresas de São Paulo, Fundação Getulio Vargas.

    • Google Scholar
26. 26
    ‘From revenue to value added taxes: welfare and fiscal efficiency effects in Brazil’

    1. S Cury
    2. AM Coelho

    (2006)

    Proceedings of the International Conference on Policy Modeling (ECOMOD 2006).

    • Google Scholar
27. 27
    mimeo

    1. S Cury
    2. AM Coelho
    3. E Pedrozo

    (2006)

    Matriz de Contabilidade Social - Brasil 2003, Relatório de Pesquisa 461/04 (Anexo 1), São Paulo, GV Pesquisa, EAESP–FGV, fevereiro, mimeo.

    • Google Scholar
28. 28
    Estudos Econômicos

    1. S Cury
    2. AM Coelho
    3. CH Corseuil

    (2005)

    739–765, A Computable General Equilibrium Model to Analyze Distributive Aspects in Brazil with a Trade Policy Illustration, Estudos Econômicos, São Paulo, IPE/FEA/USP, 35, 4.

    • Google Scholar
29. 29
    ‘The Impacts of Income Transfer Programs on Income Distribution and Poverty in Brazil: An Integrated Microsimulation and Computable General Equilibrium Analysis’. MPIA-PEP Working Paper 11086

    1. S Cury
    2. E Pedrozo
    3. AM Coelho
    4. I Callegari

    (2010)

    ‘The Impacts of Income Transfer Programs on Income Distribution and Poverty in Brazil: An Integrated Microsimulation and Computable General Equilibrium Analysis’. MPIA-PEP Working Paper 11086.

    • Google Scholar
30. 30
    Adjustment and Equity in Ecuador

    1. A De Janvry
    2. E Sadoulet
    3. A Fargeix

    (1991)

    Paris: OECD Development Center.

    • Google Scholar
31. 31
    ‘Poverty Analysis within a General Equilibrium Framework’. Working Paper 99-09

    1. B Decaluwé
    2. A Patry
    3. L Savard
    4. E Thorbecke

    (1999a)

    African Economic Research Consortium.

    • Google Scholar
32. 32
    ‘How to Measure Poverty and Inequality in General Equilibrium Framework’. Working Paper #9920

    1. B Decaluwé
    2. JC Dumont
    3. L Savard

    (1999b)

    Laval University, CREFA.

    • Google Scholar
33. 33
    General Equilibrium Models for Development Policy

    1. K Dervis
    2. J de Melo
    3. S Robinson

    (1982)

    London: Cambridge University Press.

    • Google Scholar
34. 34
    ‘From stylized to applied models: building multisector CGE models for models for policy analysis’. CUDARE Working Paper Series

    1. S Devarajan
    2. J Lewis
    3. S Robinson

    (1991)

    ‘From stylized to applied models: building multisector CGE models for models for policy analysis’. CUDARE Working Paper Series, nº. 616, University of California at Berkeley, Dept. of Agricultural and Resource Economics and Policy.

    • Google Scholar
35. 35
    ‘The impact of conditional cash transfer programs on household work decisions in Brazil’

    1. AR Ferro
    2. AC Nicollela

    (2007)
36. 36
    ‘Evidence of eligibility manipulation for conditional cash transfer programs’

    1. S Firpo
    2. R Pieri
    3. E Pedrozo
    4. AP Souza

    (2014)

    EconomiA 15:243–260.

    • Google Scholar
37. 37
    ‘The Effects of Conditional Cash Transfer Programs on Adult Labour Supply: An Empirical Analysis Using a Time-Series-Cross-Section Sample of Brazilian Municipalities’

    1. MN Foguel
    2. RP de Barros

    (2008)
38. 38
    Handbook of Labor Economics

    1. R Gronau

    (1986)

    Home Production – A Survey, Handbook of Labor Economics, 1, chapter 4, Amsterdan, North Holland.

    • Google Scholar
39. 39
    Income Distribution and Growth: A Simulation Model for Kenya

    1. WJ Gunning

    (1983)

    In: DG Greene, editors. Kenya: Growth and Structural Change. Washington, DC: World Bank. pp. 487–621.

    • Google Scholar
40. 40
    ‘Shadow Prices, Market Wages, and Labor Supply’

    1. J Heckman

    (1974)

    Econometrica 42:679–694.

    • Google Scholar
41. 41
    ‘Sample selection bias as a specification error’

    1. J Heckman

    (1979)

    Econometrica 47:153–61.

    • Google Scholar
42. 42
    Parcerias Estratégicas - Edição especial: Análise sobre a Pesquisa Nacional por Amostra de Domicílios (Pnad 2004)

    1. R Hoffmann

    (2006)

    77–88, Brasil, 2004: Menos pobres e menos ricos, Parcerias Estratégicas - Edição especial: Análise sobre a Pesquisa Nacional por Amostra de Domicílios (Pnad 2004), Brasília, Centro de Gestão e Estudos Estratégicos, 22.

    • Google Scholar
43. 43
    ‘Transferências de renda e a redução da desigualdade no Brasil e cinco regiões entre 1997 e 2004’

    1. R Hoffmann

    (2006b)

    Econômica. Rio de Janeiro 8:55–81.

    • Google Scholar
44. 44
    Comunicados IPEA

    1. IPEA

    (2012)

    A Década Inclusiva (2001-2011): Desigualdade, Pobreza e Políticas de Renda, Comunicados IPEA, 155, Sept, 25, Brasília.

    • Google Scholar
45. 45
    Boletim de Políticas Sociais - acompanhamento e análise nº 23

    1. IPEA

    (2015)

    Brasília: IPEA.

    • Google Scholar
46. 46
    ‘The welfare effects of balance of payments reforms: A macro-micro simulation of the cost of rent-seeking’

    1. D King
    2. S Handa

    (2003)

    The Journal of Development Studies 39:101–128.

    • Google Scholar
47. 47
    ‘Evaluating the economic effects of income security reforms in Switzerland: an integrated microsimulation - computable general equilibrium approach’. Working Paper

    1. T Müller

    (2004)

    University of Geneva.

    • Google Scholar
48. 48
    ‘Inter-industry wage differentials and earnings inequality in Brazil’

    1. AC Pinheiro
    2. LA Ramos

    (1995)

    Estúdios de Economia 21:79–111.

    • Google Scholar
49. 49
    ‘Redução da Desigualdade Renda no Brasil: determinantes e consequências’

    1. AH da Silva Santos

    (2013)

    ESAF - VI Prêmio SOF de Monografias.

    • Google Scholar
50. 50
    CIRPRÉ – Centre Interuniversitaire sur le Risque, les Politiques Économiques et l’Emploi. Working Paper 03-43

    1. L Savard

    (2003)

    39, CIRPRÉ – Centre Interuniversitaire sur le Risque, les Politiques Économiques et l’Emploi. Working Paper 03-43.

    • Google Scholar
51. 51
    ‘Poverty and inequality analysis within a CGE Framework: a comparative analysis of the representative agent and microsimulation approaches’

    1. L Savard

    (2005)

    Development Policy Review 23:313–332.

    • Google Scholar
52. 52
    Avaliando o Impacto do Programa Bolsa Família: uma Comparacão com Programas de TransferênciaC ondicionada de Renda de Outros Países. IPC Evaluation Note, No. 1

    1. FV Soares
    2. RP Ribas
    3. RG Osório

    (2007)

    Brasília: IPC.

    • Google Scholar
53. 53
    XIII Seminário sobre Economia Mineira – Economia, História, Demografia e Políticas Públicas

    1. PA Tavares

    (2008)

    Efeito do Programa Bolsa Família sobre a Oferta de Trabalho das Mães, XIII Seminário sobre Economia Mineira – Economia, História, Demografia e Políticas Públicas, Diamantina – MG – Brasil, agosto de.

    • Google Scholar
54. 54
    ‘Vanishing income redistributions: Keynesian clues about model surprises in the short-run’

    1. L Taylor
    2. F Lysy

    (1979)

    Journal of Development Economics 6:11–29.

    • Google Scholar
55. 55
    ‘Análise do Impacto do Programa Bolsa Família na Oferta de Trabalho dos Homens e Mulheres’

    1. CG Teixeira

    (2008)

    UNDP/IPC, http://www.ipc-undp.org/publications/mds/27P.pdf.

    • Google Scholar
56. 56
    ‘Trade liberalization and poverty in Ecuador: a CGE macromicrosimulation analysis’

    1. R Vos
    2. N De Jong

    (2003)

    Economic System Research 15:211–232.

    • Google Scholar

Author details

1. Samir Cury

   Fundação Getúlio Vargas (EAESP/FGV), Brazil

   For correspondence

   sacury@terra.com.br

2. Euclides Pedrozo

   Fundação Getulio Vargas (EESP/FGV) and Universidade Paulista, Brazil

   For correspondence

   euclides.pedrozo@fgv.br

3. Allexandro Mori Coelho

   Centro Universitário Álvares Penteado (FECAP), Brazil

   For correspondence

   allexandro_coelho@yahoo.com.br