1. Methodology
  2. Spatial microsimulation
Download icon

Validation of spatial microsimulation models: A proposal to adopt the Bland-Altman method

  1. Kate A Timmins  Is a corresponding author
  2. Kimberley L Edwards  Is a corresponding author
  1. School of Sport and Exercise Science, University of Lincoln, United Kingdom
  2. Arthritis Research UK Centre for Sport Exercise and Osteoarthritis, University of Nottingham, United Kingdom
Research article
Volume 9(2) Summer 2016
Cite this article as: K. A Timmins, K. L Edwards; 2016; Validation of spatial microsimulation models: A proposal to adopt the Bland-Altman method; International Journal of Microsimulation; 9(2); 106-122. doi: 10.34196/ijm.00137

Abstract

Model validation is recognised as crucial to microsimulation modelling. However, modellers encounter difficulty in choosing the most meaningful methods to compare simulated and actual values. The aim of this paper is to introduce and demonstrate a method employed widely in healthcare calibration studies.

The ‘Bland-Altman plot’ consists of a plot of the difference between two methods against the mean (x-y versus x+y/2). A case study is presented to illustrate the method in practice for spatial microsimulation validation. The study features a deterministic combinatorial model (SimObesity), which modelled a synthetic population for England at the ward level using survey (ELSA) and Census 2011 data. Bland-Altman plots were generated, plotting simulated and census ward-level totals for each category of all constraint (benchmark) variables. Other validation metrics, such as R2, SEI, TAE and RMSE, are also presented for comparison.

The case study demonstrates how the Bland-Altman plots are interpreted. The simple visualisation of both individual- (ward-) level difference and total variation gives the method an advantage over existing tools used in model validation. There still remains the question of what constitutes a valid or well-fitting model. However, the Bland Altman method can usefully be added to the canon of calibration methods.

1. Background

The goal of a spatial microsimulation model, in most cases, is to create a data set that mimics the ‘real-world situation’ as accurately as possible. To have confidence in the simulated data, it is necessary to validate the model, comparing the output to actual data (Edwards & Tanton, 2012). The validation process for microsimulation modelling has been broadly divided into two components: internal (in-sample, or endogenous) and external (out-of-sample, or exogenous) (Edwards & Tanton, 2012; O’Donoghue, Morrissey, & Lennon, 2014). Internal validation refers to the process of comparing values from the simulated data set to the original data set. This includes model calibration, whereby the model fit is assessed by comparing the actual and simulated values for constraining (or benchmark) variables. In-sample validation also occurs where actual and simulated outcomes are compared at an aggregate level (Ballas & Clarke, 2001). External validation occurs where values are compared against data not used in the simulation.

Although the importance of validation is widely recognised (Edwards et al., 2011), researchers still encounter difficulty in choosing the most meaningful methods to compare simulated and actual values. To date, quantitative methods for internal validation that have been proposed or used include:

A brief description of the methods appropriate for deterministic and other models is offered in Table 1. The remainder of this paper will not directly discuss techniques for deriving confidence intervals or tests for difference. Techniques to derive confidence intervals, although their potential to aid in model calibration has been well argued, are not appropriate for deterministic models, where iterative runs of the model would not result in different simulated populations. (See Voas and Williamson (Voas & Williamson, 2000) for a discussion of bootstrapping for combinatorial models). Nor will hypothesis-driven tests be included in the comparison which follows, since validation seeks to find agreement, rather than difference, and using tests for difference presume that no observed difference can be interpreted as no difference. A discussion about the hazards of ‘accepting the null hypothesis’ is elegantly described by Altman and Bland (Altman & Bland, 1995). The relative strengths and merits of these validation methods have been extensively explored by a number of reviews (Edwards & Tanton, 2012; Lovelace et al., 2015; Rahman et al., 2013; Scarborough et al, 2009).

Table 1
Methods to assess goodness-of-fit of spatial microsimulation models.
Method Description
Correlation and R2 Plots simulated area count against actual area count. The R2, or coefficient of determination, is the square of the Pearson correlation coefficient and gives an indication of fit.
Standard Error about Identity (SEI) In contrast to R2, SEI reflects the error around the line of identity (x=y; also known as the line of equality), rather than the line of best fit.
Total Absolute Error (TAE) A sum of the error (the difference between simulated and actual population counts for each area) across a category.
Standardized Absolute Error (SAE) TAE is divided by the total expected count. The standardization allows comparison between tables.
Root Mean Squared Error (RMSE) The square root of the mean squared error. Gives an indication of error dispersion (if error follows a normal distribution).
z-score, modified z-score, and zm2 The z-score is a cell level statistic that reflects the difference in the relative size of the category between actual and simulated populations. The modified score deals better with small cell counts, though an adjustment still needs to be made where area counts are 0. The zm2 is an overall measure, summing the squared z-scores.
E5 A count of the number of areas where error is greater than 5%.

One of the chief problems encountered in validation, particularly in model calibration, is that there is often a large quantity of values to compare, each with a varying degree of agreement between actual and simulated values, so that gaining an overall assessment of model fit is challenging. On the other hand, summary measures of model fit have the disadvantage of losing information (Lovelace et al., 2015). One review concluded that a combination of approaches was necessary to overcome these shortcomings (Kopec et al., 2010).

With such an arsenal of tools at modellers’ disposal, it may be questioned whether yet another suggestion is necessary. However, the demonstration and discussion which follow will make clear the advantages of a method for validation borrowed from the healthcare literature, the Bland Altman plot. In particular, the Bland Altman plot, or BA plot, is unique in its ability to illustrate both cell (area) level and overall (matrix) error.

1.1 The Bland Altman method

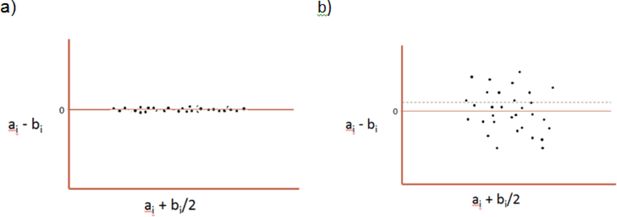
Validation techniques are commonly employed in healthcare to calibrate clinical measurement instruments. Typically, agreement between the instrument and a ‘gold standard’ is illustrated using a method proposed by Martin Bland and Doug Altman (Bland & Altman, 1986) in the 1980s. This method involves plotting the difference between two methods (x-y) against the mean (x+y/2). This enables the examination of both the absolute and relative difference, and the shape of the plot reveals how well two methods agree overall as well as across a range of values. A hypothetical example is shown in Figure 1: a) showing perfect agreement and b) showing a more typical comparison.

Figure 1
Download asset Open asset
Hypothetical illustrations of Bland Altman plots.

The method also typically incorporates a calculation of ‘limits of agreement’ (not shown in Figure 1): ±1.96*standard deviation of the differences, assuming the differences are normally distributed. These limits illustrate where 95% of differences lie. When generated with the plots the limits are typically denoted by horizontal lines

The features of the BA method have been well described and explored in the medical literature and elsewhere. Indeed, the original 1986 paper is one of the most highly cited research papers ever (Van Noorden, Maher, & Nuzzo, 2014). Discussions about its use in repeatability studies, the use of confidence intervals, and interpretation are helpfully collated on Martin Bland’s website (Bland, 2011). The method is now well established in medical measurement comparison studies. A systematic review found the method was adopted in 85% of studies validating medical instruments (Zaki et al, 2012). As a result, most standard statistical packages now include options to produce the plot with limits of agreement. In Stata, for example, BA plots can be generated using the ‘baplot’ command (Seed, 2014). Alternatively, it is possible to generate Bland Altman plots with trend lines rather than limits of agreement (using the ‘batplot’ command (Mander, 2016)) where the assumption of normally distributed error is not met (and straight limits of agreement could be misleading). In R, BA plots can be generated using the ‘MethComp’ package.

This paper is not intended as an exhaustive exposition about the relative merits and disadvantages of all the methods described in Table 1. This has been clearly and comprehensively covered by previous publications (Edwards & Tanton, 2012; Lovelace et al., 2015; Scarborough et al., 2009). Nor is it an attempt to establish a framework for validation across all spatial microsimulation types, which lies beyond the scope of its aims. Rather, the purpose is to draw attention to another evaluation method, which satisfies many of the requirements identified in the literature, not least that it is ‘fast, robust and easy to use’ (Voas & Williamson, 2001). The case study which follows demonstrates the advantage of the BA plot in calibrating a spatial microsimulation model.

2. Case study

2.1 Introduction

This case study is merely intended as an illustration to demonstrate the use of validation methods and compare these to the BA method. The principles of validation apply to many other microsimulation models, particularly those based on combinatorial optimisation. A brief description of the model is given in order to aid interpretation of the outputs.

2.2 Methods

2.2.1 The model

Data on the prevalence of osteoarthritis (OA) – a debilitating condition of the joints – are not available at a small-area level in the UK. In order to explore geographic patterns, a spatial microsimulation model created a synthetic population data set for England.

Spatial microsimulation was performed using a deterministic combinatorial optimisation method, encapsulated in an executable file, ‘SimObesity’. The model has been described previously (Edwards & Clarke, 2009). In brief, a two stage process, of deterministic reweighting followed by optimisation, is used. The model is deterministic and the order of constraint entry is inconsequential. The optimisation stage uses a ‘floor’ function to convert reweights to integers (‘whole persons’ rather than fractions which may result from the reweighting).

In this example, the data sets used were the English Longitudinal Study of Ageing (ELSA) (Marmot et al, 2015) (a nationally representative survey of older adults) and the 2011 Census data for England (Office for National Statistics, 2011). For this study, data from Wave 6 of ELSA, collected in 201213, were used (n=10,601), along with ward-level tables from the Census (England only). Wards are key UK geographic boundaries (Office for National Statistics, 2013), of which there are 7,689 in England with a mean population of ~5,500. The outcome for the model was OA. In the interests of simplicity for this case study, just two benchmarks were used: age (7 categories: 50–54yr, 55–59yr, 60–64yr, 65–69yr, 70–74yr, 75–79yr and ≥80yr) and sex (male/female). These two constraint variables were cross-tabulated.

2.2.2 The validation

BA plots were generated using the ‘batplot’ command in Stata. Scatter plots are also presented. In order to facilitate comparison with other commonly used validation methods, the following were calculated: R2, TAE, SAE, RMSE, SEI and zm2.

R2 was derived using the Stata ‘regress’ command. TAE was calculated as the sum of error terms in a constraint category (Voas & Williamson, 2000). SAE was taken as the TAE divided by the expected total population count in that category (Edwards & Tanton, 2012). RMSE is the square root of the mean squared error. SEI was calculated using the formula cited by Tanton et al (Tanton & Vidyattama, 2010). Zm2 is the sum of squared modified z-scores (zm), as suggested by Williamson et al (Williamson, Birkin, & Rees, 1998). The modified score (zm) better takes into account low cell counts. It is still unable to deal with empty cells, however. In this paper, an adjustment was made in the case of empty cells, as described by Williamson et al, where the error was used instead of the zm.

Analyses were performed using Microsoft Excel and Stata Release 13 (StataCorp, 2013).

2.3 Results

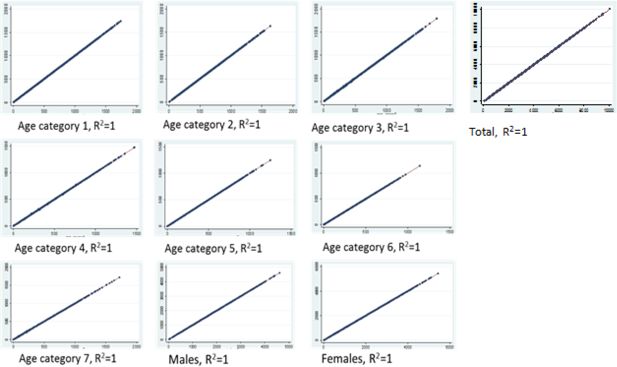
Figure 2 shows scatter plots and coefficients of determination for the ward population counts (‘Total’) as well as for each constraint category. Observed census counts are plotted on the x axis and simulated counts on the y axis.

Figure 2
Download asset Open asset
Scatter plots for age and sex categories, simulated counts versus census ward totals.

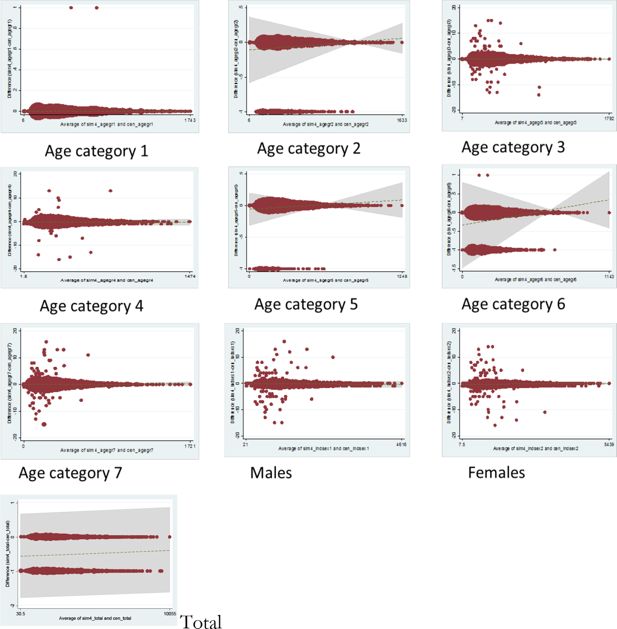
Figure 3 shows the BA plots for the same categories. In contrast to Figure 2, where the scatterplots indicate near perfect correlation, Figure 3 demonstrates the variability of counts within individual wards, as well as the heterogeneity across ward sizes. For all categories plotted, the majority of data points fit along the horizontal 0 line, showing exact agreement for these wards. However, we can also identify which categories are less well fitted: population counts for the oldest age category, for example, Category 7, have been under- or over-simulated by as much as 15 individuals for several wards. (Readers should take note of the y axis scale on each plot.) In addition, we can tell that this discrepancy is prevalent only amongst the smaller wards, with the wider spread data points confined to the left-hand side of the graph. Conversely, the simulated population in the youngest age group is almost perfectly calibrated with census data, with a discrepancy of only 1 extra individual in each of 2 wards. Finally, it can be seen that the total simulated ward counts either match exactly with census numbers or under-represent by 1 individual (this under-estimation likely reflects the flooring function employed by SimObesity in the optimisation algorithm, which prevents partial people ‘existing’ in the simulated dataset).

Figure 3
Download asset Open asset
Bland Altman plots for age and sex categories, simulated versus census ward totals.

Table 2 shows the corresponding metrics for each category: R2, SEI, TAE, SAE, RMSE, zm2 and E5. It can be seen that R2 does not reflect the differences in fit of the categories which is described by the other methods. All of the other measures agree that age group 1 is the best fitted category. This is also evident in the BA plot for age category 1, which shows just two areas differ and by just 1 individual in each. Beyond this, however, the metrics imply differing pictures about the model fit.

Table 2
Validation metrics for the comparison of simulated and census counts in each constraint category.
Category R2 SEI TAE SAE RMSE zm2 E5
Age group 1 1 1 2 0.0000006 0.016128 0.003318 0
Age group 2 1 0.999999 −522 −0.0001742 0.260556 2.175607 0
Age group 3 1 0.999991 −62 −0.0000195 0.688421 13.26152 6
Age group 4 1 0.999988 −1365 −0.0005442 0.626817 12.09789 6
Age group 5 1 0.999999 −221 −0.0001081 0.169536 2.005676 1
Age group 6 1 0.999988 −1591 −0.0009531 0.455455 14.59673 3
Age group 7 1 0.999989 −251 −0.0001029 0.689271 22.73108 22
Male 1 0.999998 −1703 −0.0001987 0.809217 6.331774 0
Female 1 0.999999 −2307 −0.0002389 0.85425 7.099424 4
Total 1 1 −4010 −0.0002200 0.722166 2.450981 0

SEI does not offer much more in the way of detail than the R2 in this example, but with perhaps a slight indication that age categories 4 and 6 contain more error. The other metrics pinpoint either the sex categories (TAE, SAE, RMSE) or age category 7 (E5, zm2) as the worst fitted. This is in keeping with the BA plots for these categories. The BA plots, however, also clearly demonstrate the absolute error for each ward relative to ward size. The E5 informs us that the error is greater than a 5% difference in 22 wards.

3. Discussion

The figures clearly demonstrate how informative the BA plot is in gauging agreement between two data sets. The case study illustrates the use and interpretation of these plots for calibrating or validating spatial microsimulation models. As far as the authors are aware, this is the first published instance of the use of the BA method in calibrating or validating a spatial microsimulation model. This case study serves merely as an illustration: in application, there would likely be many more plots to match the number of benchmark categories used as well as any variables used for external validation. The interpretation would remain the same for evaluation of external agreement. The benefits for directly comparing the fit of different models are also clear.

Table 3 summarises the strengths and weaknesses of the methods used. The following points summarise the key advantages of the BA plot.

Table 3
Summary of the strengths and weaknesses of validation methods presented.
R2 SEI TAE SAE RMSE zm Zm2 E5 BA plot
Indication of individual area error X X X X X √ X √ √
Indication of systematic (overall) bias X √ √ √ X X √ X √
Identify outliers √ X X X X √ X √ √
Indication of error distribution (by area size) X X X X √ X X X √
Handles empty cells (0 counts) √ √ √ √ √ X X X √
Comparable across models (of different sizes) √ √ X √ X √ X √ √
Single overall metric (for each category) √ √ √ √ √ X √ √ X

3.1 Key advantages of the BA plot

3.1.1 Bland Altman plots are informative about overall error and individual area error

Huang & Williamson (Huang & Williamson, 2001) stressed the importance of examining both local, cellular fit and tabular or overall fit. The latter allows an assessment of how well the model performs overall, whilst the former can be used to identify key sources of error. Local fit is typically examined using absolute or relative error or z-scores. If tables are large, it is challenging to identify which are key sources of error. The E5 is helpful in summarizing how many areas could be considered key sources of error, though it is still necessary to locate these. Most other metrics offer a summary measure of category fit (R2, SEI, TAE, SAE, RMSE, zm2). In other words, these metrics give an overall summary of the accuracy across all of the small areas. The BA plot, on the other hand, provides information both about performance across all the geographic areas (bias, limits of agreement) as well as displaying the error for each individual area which can be seen from the plot.

3.1.2 Bland-Altmanplots identify systematic bias

Some of the standard methods in use do address systematic bias: for instance the TAE, SAE and zm2 show both the overall size of inaccuracy (bias) as well as the direction of bias (whether it is an under- or over-estimation). RMSE and SEI can be said to address bias; however, in using squared values, the direction of bias is not given. The inability to detect systematic bias is one of the common criticisms of the R2 measure (Lovelace et al., 2015). In most standard statistical packages, a line of bias will be generated with each BA plot, showing for example if one measure consistently underestimates at all levels of the scale.

3.1.3 Bland-Altman plots reveal outliers

The visual representation of the error in the BA plot makes it easy to detect outliers, where error is especially large for particular areas. In Stata, data points can be labelled (using the ‘valabel’ option) so outliers can be identified, and, if necessary, potential explanations for the error investigated.

3.1.4 Bland-Altman plots can handle empty cell counts

Some calibration metrics – such as z-scores – have difficulty handling empty cells, or 0 cell counts (Williamson et al., 1998). Empty cells are not unusual in spatial microsimulation modelling, particularly where small areas are modelled. The BA plot does not entail division, therefore 0 counts are not problematic

3.1.5 Bland-Altman plots show the error distribution

It is potentially informative to see if the variation of error is consistent across all population sizes, or whether it is larger at one extreme. RMSE, although large variance at the extreme high populous areas will affect the RMSE, does not illustrate the variability across the scale. The visual spread of the data points on the BA plot would show, for example, if error was greater for larger areas (the right-hand side of the plot) or smaller areas (to the left of the plot).

3.1.6 Bland-Altman plots can be compared across models

Several authors have identified the need for ‘scale-free metrics’ (Lovelace et al., 2015). Although the BA plot cannot be said to be scale-free, it is possible to compare the visual characteristics of plots on different scales. The comparison would rely on judgement of the relative visual characteristics of the plots, rather than a directly comparable metric. Nevertheless, this is useful to illustrate the comparative goodness of fit. It is especially relevant where the models to be compared are of different sizes. Summary measures such as TAE depend not only on the size of the error, but also the size of the matrix. As shown in the example used here, where TAE was seemingly high at -4010, but this was across 7,689 wards

3.1.7 Bland-Altman plots are “robust, fast and easy to understand”

Lastly, BA plots have the distinct advantage over other methods in that they are “robust, fast and easy to understand” (Voas & Williamson, 2001). They are not computationally demanding, and are easily interpreted.

3.2 Limitations

The BA plot does not offer a simple, single metric or criterion for judgement of model performance. Rather, it offers an informative description of the error, from which an informed decision can be made. Appraisal of validity is made on a case-by-case judgement. In medicine, this decision will directly relate to the clinical relevance of any observed bias or heterogeneity. The beauty of this is that the BA plot is widely applicable across tools, and across disciplines. The potential downside is confusion surrounding the interpretation of BA plots. Bland and Altman themselves recognised some of the common difficulties in interpreting the plots (Bland & Altman, 2003). In particular, there appears to have been widespread misunderstanding of the assumptions for the calculation of limits of agreement.

In spatial microsimulation modelling, the literature reveals both criterion based approaches and more subjective approaches to model appraisal. For example, Tanton and Vidyattama (Tanton & Vidyattama, 2010) employ a criterion in validating the GREGWT model: the ‘TAE criteria’ is met where the TAE for all constraints does not exceed the population of a small area (in their paper, a statistical local error, SLA). This has the advantage of making validity assessment transparent and uniform. However, the authors themselves point out that there is no statistical basis for this criterion, and although based on modelling experience, it represents a somewhat arbitrary cut-off.

Other authors have advocated a “statistical approach” to determine if a model is valid (Rahman et al., 2013). There are difficulties in such approaches, however: chiefly, because validation seeks to assess agreement rather than difference, and therefore standard hypothesis-based approaches do not readily apply. (See Altman and Bland (1995) for a discussion regarding ‘acceptance’ of the null hypothesis.) For this reason, tests for difference (such as the t test (Edwards & Clarke, 2009)), were not included in the comparisons presented here.

The case study used in this paper to demonstrate the BA plot used a deterministic combinatorial optimisation model. Therefore, the BA plots could only be compared with validation methods appropriate to this kind of model. It is likely that there are different considerations for alternative types of model which were beyond the scope of this paper. For example, a range of further validation methods have been proposed for probabilistic models (e.g. deriving confidence intervals using multiple iterations (Tanton, 2015)) or regression-based models (this is covered well in a review of regression model validation by Scarborough et al (Scarborough et al., 2009)). Although BA plots could equally be used for these alternative models, further work would need to be carried out to examine how the method compares.

Similarly, this paper did not cover external validation, where outputs are compared to an exogenous data set. The example presented here focusses only on internal convergence of the model constraints; therefore only partially addressing the question of its validity. External validation was not performed here because the case study was merely intended as an introduction to the BA method, and also because there was not an external data set readily available. Again, further work could explore its use in all aspects of validity. often there may a trade-off between internal convergence and external validity (Tanton & Vidyattama, 2010).

4. Conclusion

This case study clearly demonstrates the added benefit of using Bland Altman plots in model validation. Bland Altman plots show not only overall agreement, but also agreement according to ward size and an indication of individual ward error, which gives the method an advantage over existing tools used in model validation. However, the Bland Altman method requires subjective judgement about whether the model fit is ‘good’. This is both a strength (in that it is not blindly interpreted on the basis of an arbitrary p value) and a weakness.

There still remains a lack of agreement among microsimulation modellers regarding what constitutes a valid or well-fitting model (Edwards & Tanton, 2012). It remains for the community to establish some form of consensus or guidance on best practice (Whitworth, 2013). It seems unlikely that there is a one-size-fits-all quantitative tool to meet all needs. The information that we require of a validation exercise – the size, direction, source and distribution of the error – is perhaps too much to ask of a single, summary measure, and it may be misguided to seek one. Comparing models according to a single measure may hide the nuanced differences between models – where one performs well for low-density areas for instance. The impact of these differences will depend on the purposes of the microsimulation. The choice of validation will remain dependent on the nature of the research (Lovelace et al., 2015), as well as taking into account comparability with previous literature and other models. Nevertheless, the Bland Altman method of assessing agreement is a useful tool to add to the canon of calibration methods.

References

  1. 1
    Statistics notes: absence of evidence is not evidence of absence
    1. DG Altman
    2. JM Bland
    (1995)
    BMJ 311:485.
  2. 2
    Modelling the local impacts of national social policies: A spatial microsimulation approach
    1. D Ballas
    2. GP Clarke
    (2001)
    Environment and Planning C: Government and Policy 19:587–606.
  3. 3
    Using SimBritain to model the geographical impact of national government policies
    1. D Ballas
    2. GP Clarke
    3. D Dorling
    (2007)
    Geographical Analysis 39:44–77.
  4. 4
    https://www-users.york.ac.uk/~mb55/meas/meas.htm
    1. JM Bland
    (2011)
    Design and analysis of measurement studies.
  5. 5
    Applying the right statistics: analyses of measurement studies
    1. JM Bland
    2. DG Altman
    (2003)
    Ultrasound in obstetrics and Gynecology 22:85–93.
  6. 6
    The design and validation of a spatial microsimulation model of obesogenic environments for children in Leeds, 69
    1. KL Edwards
    2. GP Clarke
    (2009)
    UK: SimObesity, Social Science & Medicine.
  7. 7
    Internal and external validation of spatial microsimulation models: small area estimates of adult obesity
    1. KL Edwards
    2. GP Clarke
    3. J Thomas
    (2011)
    Applied Spatial Analysis and Policy 4:281–300.
  8. 8
    Validation of spatial microsimulation models
    1. KL Edwards
    2. R Tanton
    (2012)
    R Tanton, KL Edwards, editors. NL: Springer, SBM.
  9. 9
    A comparison of synthetic reconstruction and combinatorial optimisation approaches to the creation of small-area microdata: Working Paper
    1. Z Huang
    2. P Williamson
    (2001)
    A comparison of synthetic reconstruction and combinatorial optimisation approaches to the creation of small-area microdata: Working Paper, http://pcwww.liv.ac.uk/~william/microdata/workingpapers/hw_wp_2001_2.pdf.
  10. 10
    Validation of population-based disease simulation models: a review of concepts and methods
    1. JA Kopec
    2. P Fines
    3. DG Manuel
    (2010)
    BMC Public Health 10:710.
  11. 11
    Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation
    1. DR Legates
    2. GJ McCabe Jr
    (1999)
    Water Resources Research 35:233–241.
  12. 12
    Evaluating the performance of iterative proprtional fitting for spatial microsimulation: new tests for an established technique
    1. R Lovelace
    2. M Birkin
    3. D Ballas
    (2015)
    Journal of Artificial Societies and Social Simulation 18:21.
  13. 13
    http://econpapers.repec.org/software/bocbocode/s448703.htm
    1. A Mander
    (2016)
    BATPLOT: Stata module to produce Bland-Altman plots accounting for trend.
  14. 14
    English Longitudinal Study of Ageing: Waves 0-6
    1. M Marmot
    2. e al
    (2015)
    1998–2013, English Longitudinal Study of Ageing: Waves 0-6.
  15. 15
    Spatial microsimulation modelling: a review of applications and methodological choices
    1. C Donoghue
    2. K Morrissey
    3. J Lennon
    (2014)
    International Journal of Microsimulation 7:26–75.
  16. 16
    http://infuse.mimas.ac.uk
    1. Office for National Statistics
    (2011)
    2011 Census: Aggregate data (England and Wales) [computer file].
  17. 17
    http://www.ons.gov.uk/ons/index.html
    1. Office for National Statistics
    (2013)
    Statistical wards, CAS wards and ST wards.
  18. 18
    Simulating the characteristics of populations at the small-area level: new validation techniques for a spatial microsimulation model in Australia
    1. A Rahman
    2. A Harding
    3. R Tanton
    (2013)
    Computational Statistics and Data Analysis 57:149.
  19. 19
    Validation of model-based estimates (synthetic estimates) of the prevalence of risk factors for coronary heart disease for wards in England, Health & Place
    1. P Scarborough
    2. S Allender
    3. M Rayner
    (2009)
    596–605, et al, Validation of model-based estimates (synthetic estimates) of the prevalence of risk factors for coronary heart disease for wards in England, Health & Place, 15, 2.
  20. 20
    http://fmwww.bc.edu/repec/bocode/b/baplot.ado
    1. P Seed
    (2014)
    BAPLOT: Stata module to produce Bland-Altman plots, King’s College London.
  21. 21
    Stata Statistical Software: Release 13
    1. StataCorp
    (2013)
    College Station, TX: StataCorp LP.
  22. 22
    Paper presented at the Fifth World Congress of the International Microsimulation Association (IMA)
    1. R Tanton
    (2015)
    Estimating confidence intervals in a spatial microsimulation model using survey replicate weights, Paper presented at the Fifth World Congress of the International Microsimulation Association (IMA), Esch-sur-Alzette, Luxembourg.
  23. 23
    Pushing it to the edge: extending generalised regression as a spatial microsimulation method
    1. R Tanton
    2. Y Vidyattama
    (2010)
    International Journal of Microsimulation 3:23–33.
  24. 24
    Comparing two methods of reweighting a survey file to small area data
    1. R Tanton
    2. P Williamson
    3. A Harding
    (2014)
    International Journal of Microsimulation 7:76–99.
  25. 25
    The top 100 papers
    1. B Maher
    2. R Nuzzo
    (2014)
    Nature 514:550–553.
  26. 26
    An evaluation of the combinatorial optimisation approach to the creation of synthetic microdata
    1. D Voas
    2. P Williamson
    (2000)
    International Journal of Population Geography 6:349–366.
  27. 27
    Evaluating goodness-of-fit measures for synthetic microdata
    1. D Voas
    2. P Williamson
    (2001)
    Geographical and Environmental Modelling 5:177–200.
  28. 28
    http://eprints.ncrm.ac.uk/3210/1/sme_whitworth.pdf
    1. A Whitworth
    (2013)
    Evaluations and improvements in small area estimation methodologies.
  29. 29
    The estimation of population microdata by using data from small area statistics and sample of anonymised records
    1. P Williamson
    2. M Birkin
    3. P Rees
    (1998)
    Environment and Planning Analysis 30:785–816.
  30. 30
    Statistical methods used to test for agreement of medical instruments measuring continuous variables in method comparison studies: a systematic review, Plos One
    1. R Zaki
    2. A Bulgiba
    3. R Ismail
    (2012)
    e37908, et al, Statistical methods used to test for agreement of medical instruments measuring continuous variables in method comparison studies: a systematic review, Plos One, 7, 5.

Article and author information

Author details

  1. Kate A Timmins

    School of Sport and Exercise Science, University of Lincoln, United Kingdom
    For correspondence
    ktimmins@lincoln.ac.uk

  2. Kimberley L Edwards

    Arthritis Research UK Centre for Sport Exercise and Osteoarthritis, University of Nottingham, United Kingdom
    For correspondence
    Kimberley.Edwards@nottingham.ac.uk

Publication history

  1. Version of Record published: August 31, 2016 (version 1)

Copyright

© 2016, Timmins & Edwards

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Download citations (links to download the citations from this article in formats compatible with various reference manager tools)

Open citations (links to open the citations from this article in various online reference manager services)

Categories and tags