
Microreg: A traditional tax-benefit microsimulation model extended to indirect taxes and in-kind transfers
Abstract
MicroReg is a tax-benefit microsimulation model, developed by IRPET (Regional Institute for Economic Planning in Tuscany), able to simulate the main fiscal policies for all the Italian Regions. The model is based on the EUROSTAT Survey on Income and Living Conditions (EU-SILC). In its traditional version MicroReg can simulate direct taxes and in-cash transfers, but recently it was extended in two directions. The first extension aims at adding indirect taxes to simulated tax policies, thanks to a statistical matching between EU-SILC and the Italian Household Budget Survey by Istat (National Institute of Statistics (Italy)). To improve the matching, an estimation of the level of expenditure for each EU-SILC household is added to the variables on which the matching is conditioned, by applying the relation between consumption and income estimated on the Bank of Italy Survey of Households Income and Wealth. The second extension aims at including in-kind transfers, in health and education and in household disposable income. The monetary value of in-kind transfers is estimated with the public cost of production by using national and regional administrative data. The allocation of benefits among individuals is done by following the so called "actual consumption approach", both for health and education. This paper describes MicroReg, focusing on the new extensions, and the results of an application to assess the distributive effects of fiscal policies introduced in the last few years in Italy, both on the revenue and on the expenditure side.
1. Introduction
MicroReg is a static microsimulation model, developed by IRPET (Regional Institute for Economic Planning in Tuscany) for the Region of Tuscany, which is able to simulate the main fiscal policies for all the Italian Regions. Static models usually measure the short run impact of policies, by comparing households’ income under the actual legislation and the one resulting from reform policies. In comparing the two scenarios no changes in the structure of the population or in the behavior of agents are contemplated. Compared to previous versions of the model (Betti et al., (2012), Maitino & Sciclone (2008)), the one described in this paper adds two new modules to the traditionally simulated policies (i.e. direct taxes and in-cash transfers), namely indirect taxation and in-kind transfers (in health and education)1. MicroReg is now, therefore, able to assess the regional impact of public policies as a whole, considering both revenues and expenditures. This paper is structured in three sections. The first presents the model structure. The second section describes the new modules, indirect taxes and in-kind transfers. Finally, a section concludes by presenting an application of the extended model.
2. The model structure
The model is divided in three phases: i) the choice of micro-data and the imputation of missing information, namely gross income and cadastral value, ii) the calibration of sample weights, iii) the validation of results.
2.1 The choice of micro-data and the imputation of missing information
The first phase of a microsimulation model is the choice of micro-data. In Italy many microsimulation models use the Survey on Household Income and Wealth of Bank of Italy (SHIW), which provides accurate information on income and household wealth2. MicroReg uses the EUROSTAT Survey on Income and Living Conditions (EU-SILC), since it is more representative at regional level with respect to SHIW. In this paper we describe the model built on EU-SILC 2013 (year of income 2012). However, some important information is missing in EU-SILC. Indeed, gross income and cadastral value of buildings need to be estimated.
2.1.1 The grossing-up procedure
The conversion of net to gross income can be done in different ways (Immervoll & O'Donoghue, 2001, Sutherland, 2001). A first solution is to estimate a coefficient of conversion from net to gross income in a data set where both the information are available (usually for a subset of individuals). A second solution calculates the gross income for each net income in the sample, through an analytical inversion of all existing taxes in the year in which net income is detected. The third solution is based on an iterative algorithm. For each individual in the sample, the procedure estimates a gross income starting from the original net income. Fiscal rules are then applied to the estimated gross income in order to get an estimated net income. The latter is compared with the original one. If the two values are similar with a certain margin of error, the estimated gross income is considered a good approximation; otherwise the procedure iteratively corrects the algorithm.
MicroReg uses the third approach and, in particular, a variant of the algorithm used for EUROMOD, the microsimulation model for EU member states. The net income used is the sum of several sources of taxable income for personal income tax (PIT): net individual income of employees, net income from self-employment, net income from retirement, survivor's pension, disability pension (excluding war pension), net income from redundancy funds, unemployment benefits, mobility or early retirement and net income from scholarships. Incomes from land and buildings are not included since they are considered already gross. Other incomes are excluded because they are not taxable for PIT such as healthcare liquidations, insurance and pension arrears. The iterative procedure is similar to the one described in Immervol and O’Donoghue (2001). At the first iteration an arbitrarily fixed average tax rate equal to 0.22 is applied to each net income to obtain an estimation of gross income. By applying fiscal rules to the estimated gross income an estimated net income is obtained. Then, the estimated net income is compared with the true one. When the difference is higher with respect to a certain margin of error the procedure continues—by iterating–to a new estimation of gross income, by properly correcting the initial tax rate. The procedure stops when for all sample individuals the difference between the original value and estimated net income is less than 10 euro. When the algorithm does not converge after a certain number of iterations, the procedure starts with a different value of the initial rate, randomly drawn from a uniform distribution defined in the range 0–1.
2.1.2 The estimation of cadastral values
The total gross income for PIT should include incomes from land and buildings (such as rents and cadastral values of properties). EU-SILC collects only rental income but lacks the cadastral value of properties. The only available information is the total tax paid on buildings (IMU), without distinction between the dwelling house and the others. Therefore, before estimating the cadastral value we need an allocation of the total tax paid between the two components, the dwelling house and the other buildings. Then we can apply fiscal rules to estimate cadastral values.
In MicroReg the allocation of the total property tax into the two components is made by using the official data on the tax paid for the dwelling house registered by the Ministry of Finance (MEF). In details, the estimation is made in the following three steps:
The first step in the model makes an initial split of the total tax with the following criteria:
If the individual is the owner of the dwelling house and does not own other buildings then the tax is considered paid only for the dwelling house.
If the individual does not own neither, the dwelling house nor other buildings, the tax is considered paid only for other buildings.
If the individual does not own the dwelling house but only other buildings the tax is considered paid only for other buildings.
If the individual claims to own both, the dwelling house and other buildings, the tax is initially divided in two equal parts. This is only an initial division that can change in the second part of the procedure.
In the second step the tax paid for the dwelling house is estimated as follows. From the total tax paid for dwelling houses resulting from MEF, the tax paid for dwelling houses imputed in the first step to individuals of criteria (a) is subtracted. The resulting amount is used to bind the tax paid for dwelling houses imputed in the first step to individuals of criteria (d). After this step the initial division of the total tax paid of individual of criteria (d) is corrected according to real data.
In the last step the tax paid for the other buildings is estimated for each individual, with the difference between the total tax paid declared in EU-SILC and the tax paid for the dwelling house previously estimated3.
After having obtained the two components fiscal rules can be inversely applied. Rates, as well as deductions, are regional averages of municipal rates.
i=1,...n individuals; r=1,..K Regions
In order to validate the estimation of cadastral value, Table 1 and Table 2 compare MicroReg results with official statistics when available. As expected, for what concerns the dwelling house MicroReg gives satisfactory results. Tax revenue from the dwelling house is obviously similar with respect to the official tax paid registered by the MEF, given that our estimation procedure is bound exactly to that value4. The tax paid (and the tax base) simulated by our model isclose to the estimation made by Dipartimento delle Finanze and Agenzia del Territorio (2012)5.
The validation for other buildings cannot be done by using MEF official statistics that include the tax paid from legal entities. The comparison can instead be made with data registered in Dipartimento delle Finanze and Agenzia del Territorio (2012), which distinguishes between individuals and legal entities. Both the tax base and the tax revenue are under-estimated in MicroReg with respect to official data by Dipartimento delle Finanze and Agenzia del Territorio (2012). However, it is worth noting that official data include buildings owned by individuals used for productive reasons that can be under-reported in EU-SILC.
Validation of the estimation of cadastral value and IMU – billion euro.
| Tax base (cadastral value) | Total tax paid on buildings (IMU) | ||||
|---|---|---|---|---|---|
| MicroReg | Dip. Fin. and Agenzia del Territorio | MicroReg | Dip. Fin. and Agenzia del Territorio | MEF | |
| Dwelling house | 11.6 | 11.4 | 3.8 | 3.3 | 4.0 |
| Other buildings | 5.2 | 9.3 | 6.5 | 9.3 | 19.7 |
| Total | 16.7 | 20.7 | 10.3 | 12.6 | 23.7 |
-
Source: MicroReg, Agenzia del Territorio, Ministry of Finance.
According to our simulation about 52.3% of Italian taxpayers own a dwelling house (Table 2). Not surprisingly, as underlined also in Pellegrino et al. (2011), the value is higher with respect to the one registered by the MEF since taxpayers, who use the “770” form do not have to declare the ownership of the main residence. The average cadastral value of the dwelling house is about 500 euro in MicroReg and 491 euro in MEF. It increases from 415 euro in the first income class to 807 euroin the last, with a similar trend to official data. For what concerns the other buildings the model predicts that about 28.8% of taxpayers has a positive cadastral value. The tax base increases with income classes with a higher rate than the dwelling house.
Distribution of the dwelling house and the other buildings by gross income classes.
| Dwelling house MicroReg | Dwelling house MEF | Other buildings MicroReg | ||||
|---|---|---|---|---|---|---|
| Gross income classes (euro) | Households (%) with positive cadastral value | Mean cadastral value (euro) | Households (%) with positive cadastral value | Mean cadastral value (euro) | Households (%) with positive cadastral value | Mean cadastral value (euro) |
| Until 2,500 | 31.5 | 415 | 27.3 | 452 | 19.5 | 374 |
| 2,501 to 5,000 | 32.4 | 383 | 18.4 | 432 | 17.9 | 390 |
| 5,001 to 10,005 | 47.3 | 448 | 26.9 | 405 | 23.8 | 340 |
| 10,006 to 15,000 | 48.2 | 474 | 40.5 | 430 | 26.7 | 379 |
| 15,001 to 26,000 | 54.9 | 484 | 48.4 | 445 | 27.9 | 376 |
| 26,001 to 29,000 | 64.5 | 535 | 59.9 | 492 | 35.9 | 419 |
| 29,001 to 35,000 | 66.6 | 544 | 64.2 | 526 | 40.3 | 480 |
| 35,001 to 50,000 | 67.5 | 585 | 67.8 | 592 | 41.4 | 586 |
| 50,001 to 60,000 | 64.9 | 647 | 69.8 | 683 | 45.9 | 743 |
| 60,001 to 70,000 | 71.1 | 775 | 70.7 | 730 | 45.9 | 626 |
| 70,001 to 100,000 | 72.4 | 797 | 72.0 | 796 | 53.1 | 862 |
| 100,101 to 150,000 | 74.2 | 750 | 72.8 | 916 | 57.3 | 871 |
| 150,001 to 200,000 | 82.6 | 816 | 72.0 | 1,056 | 65.7 | 947 |
| Over 200,000 | 69.9 | 807 | 69.7 | 1,322 | 66.4 | 1564 |
| Total | 52.3 | 501 | 43.8 | 491 | 28.8 | 435 |
-
Source: MicroReg and Ministry of Finance.
2.2 The calibration
This procedure is performed to make estimates of gross income more similar to real data of the MEF and therefore to tackle the problem of tax evasion. Usually in a survey under the guarantee of anonymity, people are more honest than when the counterparty is the tax authority. The calibration binds the original sample weights to the joint distribution of individuals by income class (taken from the MEF) and by socio-demographic variables derived from ISTAT. The total income considered for the calibration is the one used in the grossing up procedure, plus incomes from buildings obtained after the estimation of cadastral values.
In literature two types of calibration methods can be found: i) independent calibration and ii) integrative calibration. The independent calibration allows calibrating weights with households’ variables independently from individual’s variables. The convergence procedure is generally fast, but it generates different weights for households and individuals. Integrative calibration takes into account households’ and individuals’ variables together. It converges more slowly, but households’ and individuals’ weights are the same (as requested by the European Commission Regulation for the SILC). In MicroReg an integrative calibration is performed with the following constraints: taxpayers by income classes and prevailing source of income; population by age, sex, gender and level of education; population by region of residence and by number of family members.
2.3 The validation
After having imputed missing information (see Section 2.1) and calibrated sample weights (see Section 2.2) we simulate all fiscal rules that every taxpayer follows to pay PIT in the following way:
According to Italian fiscal rules, every taxpayer can deduct the value of the main residence6 and other expenses (such as expenditure for disabled family members or for donations) from gross income. Since EU-SILC does not collect detailed information about deductible expenses, we impute their value to each taxpayer by applying a coefficient equal to the ratio between deductions and gross income by gross income classes calculated on official data from the MEF7. Taxable income is then simulated by subtracting deductions from gross income tax for each taxpayer.
Gross PIT is simulated by applying the legal tax rates to the simulated taxable income.
Each taxpayer can subtract different types of tax credits from gross PIT: i) tax credits by income source, ii) tax credits for family members and iii) other tax credits (for health expenditure, housing works, etc.). Tax credits by income source and for family members are simulated in the model since detailed information on income and household components are collected in EU-SILC. The other tax credits, similar to tax deductions, are estimated by applying to each taxpayer a coefficient given by the ratio of tax credits and gross income by gross income classes registered by MEF8.
Finally, the net PIT is simulated by detracting simulated and imputed tax credits from gross PIT. When PIT is positive, regional additional income tax is simulated by applying the different fiscal rules of each region.
In order to validate the model, the results of our simulations are compared with data from the MEF. Table 3 compares the distribution of the total number of taxpayers by prevailing income source resulting from the model with respect to official statistics. The total number of taxpayers in the model is in line with the real one and the composition is very similar to the one of the MEF. These satisfactory results are expected given that one of the constraints of our calibration procedure (see Section 2.2) is the distribution of taxpayers by source of income and gross income classes.
Taxpayers by prevailing income source (millions).
| MicroReg | MEF | Diff. (%) | |
|---|---|---|---|
| Employee income | 20.02 | 20.02 | 0.0 |
| Retirement income | 14.22 | 14.22 | 0.0 |
| Self-employed income | 4.60 | 4.60 | 0.0 |
| Other sources of income | 1.69 | 1.68 | 0.3 |
| Total | 40.54 | 40.53 | 0.0 |
-
Source: MicroReg and Ministry of Finance.
Table 4 compares aggregate fiscal amounts simulated by the model with official data from the MEF9. The model is able to simulate quiet gross income, taxable income, gross and net PIT well. A little less accurate is the simulation of tax credits for family members. Results are in line with other microsimulation models. In Ceriani et al. (2016) the model over-estimates gross income by 3% and PIT by 1%. In Pellegrino et al. (2011) the average gross income is 97.5% of the real one. Models that also use administrative data obtain better results. In Di Nicola et al. (2015) a microsimulation model is built on a dataset that matches EU-SILC with administrative data on PIT and real estate datasets. Their results are very close to official statistics,except for municipal taxes, where the difference in amounts between the model and the MEF is lower than 1%.
Validation of the model – income year 2012 (billion euro).
| MicroReg | MEF | Diff. (%) | |
|---|---|---|---|
| Gross income | 790.9 | 800.4 | −1.2 |
| Deductions | 23.7 | 24.0 | −1.2 |
| Taxable income | 767.2 | 773.6 | −0.8 |
| Gross PIT | 205.1 | 208.2 | −1.5 |
| Tax credits by income source | 41.5 | 41.6 | −0.3 |
| Family tax credits | 11.7 | 11.5 | 2.3 |
| Net PIT | 151.3 | 152.3 | −0.6 |
| Regional additional income tax | 11.0 | 11.0 | −0.5 |
-
Source: MicroReg and Ministry of Finance.
Figure 1 shows the density function by gross income classes simulated by MicroReg and registered by MEF10. The overall distribution of gross income simulated by the model is close to the real one with some specific limits. The model under-estimates the number of taxpayers under 1,000 euro and over-estimates between 7,500 and 10,000 euro. The under-estimation in the first class depends on a typical problem of under-reporting on small amounts of income in EU-SILC11. We do not correct for this under-reporting problem since taxpayers under 1,000 euro represents a small part of the total that do not pay PIT. The over-estimation of taxpayers between 7,500 and 10,000 euro is partially offset by a small under-estimation of taxpayers between 6,000 and 7,500 euro.
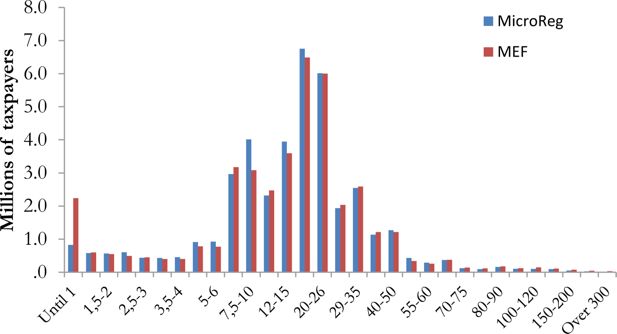
Frequency density function for gross income – income year 2012.
Note: The total number of taxpayers is 40.5 millions.
Source: MicroReg and Ministry of Finance.
Figure 2 reports the distribution of taxpayers with positive net PIT by gross income classes12. The distribution of simulated PIT is quite similar with respect to official statistics. The number of taxpayers with positive PIT is 32.3 million in MicroReg against 31.2 million in official data of the MEF.
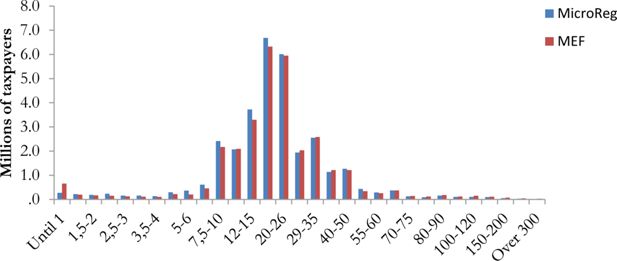
Distribution of taxpayers by gross income classes – net PIT – income year 2012.
Note: The total number of taxpayers with positive net PIT is 32.3 million.
Source: MicroReg and Ministry of Finance.
Table 5 finally shows the main redistributive indexes calculated at the taxpayer level. The pre-tax Gini coefficient is about 0.42. After the PIT the Gini becomes 0.38 with a decreasing of 0.05. The strong redistribution is given by the combination of an average tax rate of 0.19 and a strong progressive tax (Kakwani index of 0.22). As expected, the redistributive effect of regional additional income tax is lower with respect to PIT. Indeed, several regions apply a proportional additional tax and others impose a less progressive system of tax rates than PIT.
Redistributive indexes.
| PIT | Regional additional income tax | Total | |
|---|---|---|---|
| Pre-tax Gini | 0.4234 | 0.4234 | 0.4234 |
| Post-tax Gini | 0.3714 | 0.4223 | 0.3692 |
| Average tax rate | 0.1913 | 0.0139 | 0.2051 |
| Reynolds-Smolensky net redis. effect | 0.052 | 0.0011 | 0.0543 |
| Kakwani progressivity index | 0.2223 | 0.0769 | 0.2125 |
| Reranking | 0.0005 | 0.0000 | 0.0006 |
-
Source: MicroReg.
3. Extensions of the model
MicroReg was recently extended to indirect taxes and in-kind transfers (health and education). Indirect taxes are estimated for all Italian Regions (multi-regional model), while in-kind transfers are quantified only for the Region of Tuscany (for which data is available).
3.1 Indirect taxes
One of the recent developments of MicroReg is the simulation of indirect taxes after a matching of EU-SILC with a database on consumption. An integrated database can be used with many aims: to analyse saving and consumption behaviour; to study consumption of durable or not durable goods; to make multidimensional analysis of poverty; and to study the impact of fiscal policies.
Despite the large availability of sample surveys, it does not exist a unique survey which collects information both on income (y) and consumption (z with a minimum level of accuracy and details. Basically, given the variables x,y,z,, where x is a set of households ‘characteristics, the database lacks completely or partially, the joint observation of all three. The only way to integrate the two datasets is to assume that information in x is sufficient to jointly determine both y and z. Literature suggests many solutions to integrate the two datasets (Decoster et al., 2007). Basically, at least two approaches can be distinguished and they are explained in the following.
One, the so called explicit approach, uses Engel curves to impute expenditure to the income database. According to this approach a regression of each expenditure share variables common to the consumption and the income database (usually disposable income and socio-demographic characteristics) is estimated on the consumption database. Then, the estimated coefficients are applied to records in the income database to impute expenditure shares for each good. An application of this procedure in Italy is in O’Donoghue et al. (2004). The survey which collects information on income is the SHIW, while the consumption database is the Italian Household Budget Survey (HBS). In the latter a variable on disposable income is collected (even if underestimated), so a regression of total consumption on income and socio-demographic characteristics is estimated. The estimated coefficients are then applied to SHIW to impute total consumption. Budget shares of total consumption are subsequently estimated in HBS trough Engel curves and applied to the imputed total consumption in SHIW. The explicit approach is more recently applied in Taddei (2012), where the income database is EU-SILC and the consumption one is HBS. The procedure is made in two steps. Taddei (2012) first applies a statistical matching to impute income from EU-SILC to HBS. Once imputed income to HBS by following the explicit approach, it estimates Engel curves to associate to each observation in EU-SILC a vector of budget shares for each consumption good.
The second approach, called implicit approach, tries to find for each household of the income database the most similar in the consumption database. This approach is not based on a statistical model or on theoretical assumptions that explain consumption behaviour, but on a statistical matching (D’Orazio et al., 2002). The matching links similar units through a distance function that should be minimized. Units are compared according to a set of socio-demographic characteristics, common to the two databases. The matching can be done only if the two surveys are random samples extracted from the same population. In Italy a statistical matching between the Bank of Italy Survey of Households Income and Wealth and HBS is in Battellini et al. (2009), in which the integrated database is mainly used to compile Social Accounting Matrices (SAM). More recently, in Pisani and Tedeschi (2014) a matching technique is applied to build an integrated dataset useful for direct and indirect tax benefit microsimulation models13. The income database is the Bank of Italy Survey of Households Income and Wealth and the consumption one is HBS. Before doing the matching, Pisani and Tedeschi (2014) estimate a propensity score to synthesize in one scalar all the different variables common to the two databases. The propensity score is indeed the estimated probability to belong to SHIW conditioning on the common set of characteristics. Then, they apply two different matching procedures. In the first one they associate to each observation in SHIW the one in HBS with the closest propensity score (nearest neighbour within calliper). In the second they use a function (called Mahalanobis) to measure for each unit in SHIW the distance to all units in HBS in the common variables (included the propensity score). The unit in HBS with the lower distance is then associated to each unit in SHIW. According to Pisani and Tedeschi (2014) the Mahalanobis distance function performs better than the nearest neighbour method.
In MicroReg an implicit approach based on a matching between EU-SILC and HBS is implemented. Therefore, our method is not parametric as the ones used in O’Donoghue et al. (2004) and Taddei (2012), but it is more similar to Pisani and Tedeschi (2014). The objective of the matching is to link each family in EU-SILC to the most similar in HBS, given the set of common observable variables. The matching is shown in detail in the following three steps:
Preliminarily a comparison between the common variables is made by using a T-test for the mean difference and a X2test for equality of distribution (results are reported in appendix, Tables A.4 and A.5). After, variables are standardized with the same classifications and encodings and aggregated at household level.
Secondly, we select the conditioning variables for the matching. We do not estimate a propensity score, as in Pisani and Tedeschi (2014), but we select among the distinct common variables. The common set of variables is selected by making a regression of consumption on socio-demographic characteristics (see results for the Centre of Italy in appendix, Table A.6). Some variables refer to households characteristics (such as residence area, number of components, number of rooms, presence of loan to pay, personal computer and dishwasher ownership, access to internet). Other variables refer to sociodemographic characteristics of household components (number of children, number of adults, type of work, number of earners).
In order to improve the matching, for each EU-SILC household an estimation of total consumption is added to the set of common variables. More precisely, a regression of total consumption on household income is estimated for income quintiles in the Bank of Italy Survey of Households Income and Wealth. Indeed, SHIW collects detailed information on income, but also an aggregate measure of consumption. Then, estimated coefficients are applied to EU-SILC households to find the imputed total consumption that can be used in the matching.
Similarly to Pisani and Tedeschi (2014) we define a proximity function to integrate household by household information collected from both surveys. Our matching is made in two steps. A first exact matching for a selection of common variables (geographical area and number of components) is implemented. The exact matching allows linking each EU-SILC household with the corresponding HBS household, given the two selected variables. For the other variables the following proximity function is defined:
(3)(4)
Basically, the distance function counts for every household in EU-SILC, the number of variables with the same value in EU-SILC and in HBS. The total consumption is considered equal if the difference is lower than 1,000 euro. Finally, for each EU-SILC household the HBS household with the higher number of variables with the same value is associated. When two HBS household have the same number of equal variables the household with the lower difference of total consumption is linked.
In the integrated database the Value Added Tax (VAT) rates by type of expenditure are inversely applied to find the production price (HBS collect retails prices which include indirect taxes). Given the tax base VAT can subsequently be simulated.
The following statistics are used to validate the matching procedure and the VAT simulation. In line with expectations, the food share is higher in the South of Italy than in the North-Centre (Table 6) and the propensity to consume decreases by income deciles (Table 7).
Food share by geographical area.
| Area | Expenditure (euro) | Income (euro) | Food share |
|---|---|---|---|
| North West | 487.5 | 2,454.80 | 0.1986 |
| North East | 446.1 | 2,450.70 | 0.182 |
| Centre | 504.3 | 2,356.50 | 0.214 |
| South | 506.7 | 1,893.80 | 0.2675 |
| Italy | 488.7 | 2,259.20 | 0.2163 |
-
Source: MicroReg.
Propensity to consume by income deciles.
| Decile | Italy |
|---|---|
| 0 | 1.26 |
| 1 | 1.07 |
| 2 | 0.96 |
| 3 | 0.93 |
| 4 | 0.87 |
| 5 | 0.83 |
| 6 | 0.78 |
| 7 | 0.76 |
| 8 | 0.69 |
| 9 | 0.56 |
| Total | 0.92 |
-
Source: MicroReg.
The total VAT base is about 419 billion euro while tax revenue is 58 billion14 (Table 8). The validation of the simulation of VAT is not an easy task, as Taddei (2012) underlines, since official statistics about the revenue deriving from households are not available. As expected, our simulated tax revenue is lower with respect to the official data estimated by ISTAT (2016)15 (about 94 billion euro). Indeed, the official data includes the tax paid from public administration, no-profit institutions and others that, on the contrary, is not included in our simulation on final consumption of households. According to Taddei (2012) the percentage of total revenue that derives from households is about 70%. D’Agosto et al. (2012) estimates that about 68% of the potential tax revenue depends on final consumption of households. By applying these percentages to the total tax paid estimated by ISTAT (2016) a value around 64–66 billion is obtained, not very far from our result (58 billion euro). Further, our simulated tax revenue is in the middle between the one obtained by Taddei (2012), about 72 billion euro, and the one simulated by Gastaldi et al. (2014), around 49 billion euro.
VAT tax base and revenue (billion euro).
| VAT rate | Tax base | Tax revenue |
|---|---|---|
| 4% | 77.9 | 3.1 |
| 10% | 166.8 | 16.7 |
| 22% | 174.2 | 38.3 |
| Total | 418.8 | 58.1 |
-
Source: MicroReg.
Finally, Table 9 shows redistributive indexes, calculated at household level, for each VAT rate. Not surprisingly, VAT has a negative redistribution role. Indeed, the Gini of disposable income increases after the tax. Among the different rates, it is easily to see that the reduced rate (4%) has the most regressive impact with a negative Kakwani of 0.21. The reduced rate is applied to those essential goods that each household needs and, consequently, the fiscal burden is higher for lower incomes. Despite this, the ordinary rate shows the strongest negative redistributive effect owing to the highest average tax rate.
Redistributive indexes.
| VAT rate | 4% | 10% | 22% | Total |
|---|---|---|---|---|
| Pre-tax Gini | 0.3009 | 0.3009 | 0.3009 | 0.3009 |
| Post-tax Gini | 0.3017 | 0.3040 | 0.3059 | 0.3102 |
| Average Tax Rate | 0.0039 | 0.0208 | 0.0470 | 0.0717 |
| Reynolds-Smolensky net redis. effect | −0.0008 | −0.0031 | −0.0050 | −0.0093 |
| Kakwani progressivity index | −0.2116 | −0.1426 | −0.0931 | −0.1139 |
| Re-ranking | 0.0000 | 0.0001 | 0.0004 | 0.0005 |
-
Source: MicroReg.
In conclusion, the matching results and the simulation of VAT are satisfactory and in line with expectations. The indirect tax module of MicroReg can then be used to simulate different scenarios of VAT reforms.
3.2 In-kind transfers
The second extension of MicroReg concerns in-kind transfers16. Many empirical studies about inequality and poverty do not consider benefits from public expenditure in in-kind transfers like education, health, transport and so on. The monetary disposable income is, however, only a part of the household welfare, which depends also on the public subsidies for the production and the financing of services. The inclusion of in-kind transfers in a microsimulation model allows: i) to compare their distributive impact with respect to in-cash transfers, ii) to make a more correct comparison between countries which have a different composition of in-cash and in-kind transfers, iii) to monitor the effects of cuts in services and spending reviews.
In order to estimate the distributive effects of in-kind transfers many methodological issues should be addressed (Gigliarano & D’Ambrosio, 2009). The first issue refers to the imputation of a monetary value to in-kind transfers. Usually the monetary value is quantified by estimating the average production cost of the public sector, even if this approach has several limits. For example, it does not take into account that differences in production costs could depend on differences in the quality of services, in inefficiency or on different costs of inputs.
Once quantified the monetary value, in-kind transfers should be imputed to the individuals/households of the sample (in our case EU-SILC). In literature, two approaches have been used, the actual consumption approach (AA) and the insurance value approach (IA).
The AA imputes the monetary value of in-kind transfers only to individuals who actually use the service. The advantage of this approach is that it considers the true usage of services and it takes into account individuals’ differences. Disadvantages are many. First, the attribution is not independent on the time interval considered, during which the use of services could be entirely random. Second, it does not consider different needs of families. For example, it can impute a large monetary value to old people who need many health services with a consequent strong re-ranking (old people become richer than people with more income who do not use services).
The IA imputes to every individual an average monetary value of in-kind transfers by demographic characteristics (usually age and gender), without taking into account the actual use of services. In health, for example, a sort of insurance premium against diseases is imputed to all individuals by demographic characteristics. According to the IA, the use of health services should not depend on random reasons (as in the AA), but on demographic differences. Also this approach, however, has some disadvantages. The possibility to have a re-ranking is still present (even if less likely than in the AA) and it does not take into account individuals’ differences.
In literature the AA is often applied for education. In health the debate is more open. In studies that compare both the approaches, it has been noticed a higher distributive impact of IA than AA (Baldini et al., 2007).
In evaluating the distributive impact of in-kind transfers further methodological issues must be addressed. Usually the long run effects of in kind-transfers (like education returns) are not considered in empirical studies. Further, there is no consensus about the correct counterfactual (the starting income) that should be used to evaluate the distributive effect of in-kind transfers and about the equivalence scale that should be used. Moreover, studies about in-kind transfers typically neglect externalities. In other words, by imputing the benefit only to students or to patients they under-estimate the positive externalities of education and health on the entire population.
In MicroReg the monetary value of in-kind transfers is quantified with the cost of production of the public sector. The monetary value is imputed to individuals through the AA approach, both for education and for health. The equivalence scale is not used for in-kind transfers, but a per-household member in-kind value is attributed to each individual. The modified OECD scale is used only for the monetary disposable income. In what follows methodological choices and data used for education and health are described in details. The simulation of in-kind transfers is performed only for the Region of Tuscany, both for education and health17.
3.2.1 From pre-school to secondary education
To quantify the cost of production of pre-school, primary school, middle school and high school data from the balance sheet of the national government are used. Indeed, the biggest part of public expenditure derives from the central level. So, the total expenditure for each level of education is taken from balance sheets. Then, the regional expenditure is estimated by applying the distribution of teachers by Region to the national expenditure. The per-student value of education is afterwards estimated by dividing the total regional expenditure by the number of students (taken from the Ministry of Education) for each level of education. Finally, the per-student value is imputed to students by exploiting the information about the school attended, collected in EU-SILC, and about the age of children.
3.2.2 Higher education
In order to find the monetary value of higher education, first the cost of production is calculated and second taxes paid by each student are simulated. To quantify the cost of production the balance sheets of the three Tuscan universities (Florence, Pisa and Siena)18 are used. The per-student value is obtained by dividing the total cost of production by the number of students (taken from the Ministry of Education). University taxes are composed of three parts: entry fee, fee for the right to study and contributions. The first two are a fixed amount; the third depends on a mean test instrument called ISEE (Equivalent Economic Situation Indicator). ISEE and taxes are simulated in the model for each student. The net benefit from tertiary education is given by the difference between the per-student cost of production and simulated taxes. The net per-student value is imputed to students by exploiting the information collected in EU-SILC.
3.2.3 Health services
For health in-kind transfers administrative data from the Region of Tuscany (year 2010) are exploited. Administrative data collects both the numbers of users and the costs of production for each health service that is hospital services (cards hospital discharges), outpatient services, pharmaceutical services and rehabilitation services19. To attribute health consumption to individuals we applied the Monte Carlo method. First, a probability to consume a certain service is estimated for intersections (cells) of socio-demographic characteristics (gender, citizenship, age classes and level of education). Second, the service is attributed to individuals by comparing the estimated probability with a random number from a uniform distribution in the interval 0–1. For the selected individuals the in-kind benefit of each service (evaluated by its cost of production) is imputed.
3.2.4 The distributive impact of in-kind transfers
The incidence of simulated in-kind transfers on income by quintiles of equivalent disposable income shows the important distributive role of public expenditure, both in education and health (Figures 3 and 4).
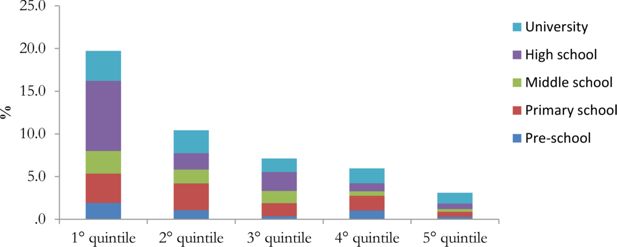
Incidence of education transfers on disposable income by equivalent household disposable income quintile – Tuscany.
Source: MicroReg.
In education, the incidence clearly decreases with income and it is particularly high in the first quintile for high and middle school. The incidence is lower for pre-school even if still decreasing with income (Figure 3). Also health expenditure seems to affect more low income quintiles. Among the different services considered hospital ones tend to have a stronger impact (Figure 4).
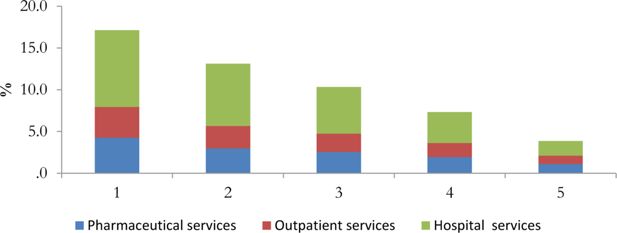
Incidence of health transfers on disposable income by equivalent household disposable income quintile – Tuscany.
Source: MicroReg.
These descriptive results are confirmed by the redistributive indexes (Table 10) calculated at the individual level. All in-kind transfers in education have a positive redistributive impact like in Baldini et al. (2007). Further, similarly to Baldini et al. (2007) the stronger redistribution derives from primary, middle and high school. The progressivity index is particularly elevated for middle and high school. The reduction in the post-transfer Gini index is lower for pre-school and university. Pre-school has a high progressivity, but a low incidence. University is the less progressive education in-kind transfer.
Redistributive indexes for in-kind transfers – Tuscany.
| Pre-transfer Gini | Post-transfer Gini | Avg. tax rate | Reynolds-Smolensky net redis. effect | Kakwani Progressivity index | Re-ranking | |
|---|---|---|---|---|---|---|
| Pre-school | 0.2838 | 0.2825 | 0.0050 | 0.0013 | 0.3186 | 0.0002 |
| Primary school | 0.2838 | 0.2808 | 0.0113 | 0.0030 | 0.3268 | 0.0006 |
| Middle school | 0.2838 | 0.2814 | 0.0068 | 0.0024 | 0.4062 | 0.0004 |
| High school | 0.2838 | 0.2776 | 0.0134 | 0.0062 | 0.5221 | 0.0007 |
| Total school | 0.2838 | 0.2712 | 0.0365 | 0.0126 | 0.4122 | 0.0019 |
| University | 0.2838 | 0.2824 | 0.0127 | 0.0014 | 0.2165 | 0.0014 |
| Pharmaceutical services | 0.2838 | 0.2802 | 0.0147 | 0.0036 | 0.2585 | 0.0001 |
| Outpatient services | 0.2838 | 0.2806 | 0.0129 | 0.0032 | 0.2544 | 0.0001 |
| Hospital services | 0.2838 | 0.2792 | 0.0305 | 0.0047 | 0.3250 | 0.0050 |
| Total health services | 0.2838 | 0.2731 | 0.0582 | 0.0107 | 0.2924 | 0.0054 |
-
Source: MicroReg.
According to our simulation, as in Baldini et al. (2007), but different with respect to Sonedda and Turati (2005)20, health services decrease inequality. Inequality diminishes especially thanks to hospital services that have the higher incidence and progressivity. Different with respect to pharmaceutical and outpatient services, hospital services are concentrated on old people and their cost of production can be very high. Consequently, as in Baldini et al. (2007), hospital services have a strong re-ranking effect.
4. An application of the extended model
The extended microsimulation model allows to evaluate the effect of fiscal policies both on the revenue and the expenditure side. In the last few years in Italy the central government implemented many fiscal policies. In this paper three polices are considered.
The first is the introduction of the “fiscal bonus” (law 190/2014 so called Stability Law for 2015). The Stability Law confirms the “fiscal bonus” for employees, introduced for the first time in 2014, with effects from 2015 onwards. The government expects from the “fiscal bonus” indirect positive effects on consumption. More precisely, the “fiscal bonus” is a fixed amount of 960 euro per year (80 euro per month) for employees with gross income under 24,000 euro and it is decreasing for employees with gross income between 24,000 and 26,000 euro, as explained in the following table (Table 11). The bonus is attributed to employees with a gross PIT higher than tax credit for employees.
Fiscal bonus scheme.
| Income (euro) | Fiscal bonus (euro) |
|---|---|
| Under 24,000 | 960 |
| Between 24,000 and 26,000 | 960* [1−(income−24,000)/(26,000–24,000)] |
| Over 26,000 | 0 |
-
Source: Stability Law for 2015.
The second policy is the safeguard clause about the increase of VAT (law 190/2014 so called Stability Law for 2015). In Italy three VAT rates are applied: the ordinary rate is now 22%, the decreased rate is 10% and concerns tourist services and some types of food, and the minimum rate is 4% for basic necessities. The law 190/2014 states that VAT rates will increase from 10% to 12% and from 22% to 24% in 2016 if other resources to meet budget constraints will not be found (safeguard clause). In the following years further increases are established (see Table 12).
VAT rates: safeguard clause.
| Year | Ordinary rate | Decreased rate |
|---|---|---|
| 2015 | 22% | 10% |
| 2016 | 24% | 12% |
| 2017 | 25% | 13% |
| 2018 | 25.5% | 13% |
-
Source: Stability Law for 2015.
The third policy is the variation in health and education expenditure between 2013 and 2016 as expected by the estimated budget of the State and by the Economic and Financial Document (DEF) 2015. In the last few years the central government decided for many cuts and spending review operations (Table 13). Between 2013 and 2016 there will be a decrease in education public spending and an increase in health (current prices). These variations (in percentage) are applied to the monetary value of in-kind transfer estimated in MicroReg to evaluate the redistributive effects.
Education and health expenditure (million euro) — Italy.
| Year | School | University | Health |
|---|---|---|---|
| 2013 | 41,899 | 6,997 | 110,044 |
| 2016 | 41,028 | 6,931 | 113,372 |
-
Source: DEF 2015 and budget of the State.
In order to evaluate the total distributive effects of the three policies we compare the disposable income in 2013 (without the fiscal bonus and the increase in VAT and with the 2013 value of in-kind transfers) and the disposable income in 2016 (with the fiscal bonus, the increase in VAT and with the 2016 value of in-kind transfers) (Figure 5).
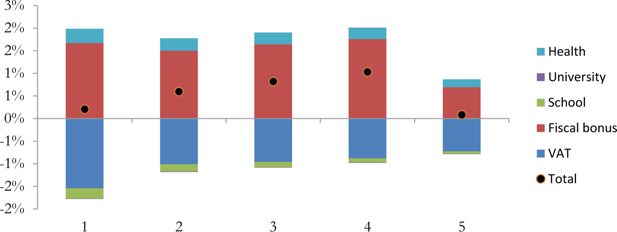
Variation of household disposable income and its components by equivalent disposable income quintiles – Tuscany.
Source: MicroReg.
The fiscal bonus has a strong effect and it is more favourable to central quintiles. It costs about 656 million of euro and it includes 788 thousands of beneficiaries in Tuscany (about 21% of the total population that lives in the 38% of the total number of households).
The increase in VAT rates has a clear regressive impact, since the disposable income is reduced more for the first quintile with respect to the others. Similar results are in Arachi et al. (2012). By simulating an increase to 23.5% and to 12.5% in the ordinary and the reduced tax rate they observe a regressive redistribution.
Cuts in school expenditure have a clear regressive impact since the decrease in disposable income is decreasing by quintile of income. The effect of reduction in university expenditure is negligible. The increase in disposable income due to the raise in health expenditure is higher for the first quintiles of income. By considering all the three policies together the effect is positive for central quintiles, with a variation in disposable income of about 0.8% (thanks especially to the fiscal bonus). For the first and the last quintile, the increase in disposable income is lower. Therefore, if the increase in VAT rates will not be avoided the positive effect of the fiscal bonus on consumption expected by the national government (most from the first quintile) could miss.
Redistributive indexes – Tuscany.
| Gini | Theil | |
|---|---|---|
| Original disposable income | 0.2836 | 0.1450 |
| Disposable income with VAT increase | 0.2851 | 0.1470 |
| Disposable income with fiscal bonus | 0.2815 | 0.1426 |
| Disposable income with variation in school expenditure | 0.2838 | 0.1451 |
| Disposable income with variation in university expenditure | 0.2836 | 0.1450 |
| Disposable income with variation in health expenditure | 0.2834 | 0.1447 |
| Final disposable income | 0.2829 | 0.1445 |
-
Source: MicroReg.
Inequality indexes, calculated at household level, confirm these results (Table 14). After the increase in VAT the Gini increases. On the contrary, it decreases with the introduction of fiscal bonus. In-kind transfers have positive effect in inequality. When their value decreases (school and university) the Gini increases, the opposite when their value increases (health).
Footnotes
1.
Due to data availability the model is extended to in-kind transfers only for the Region of Tuscany.
2.
However, also in SHIW households’ wealth is highly under-estimated.
3.
Second homes (when more than one) are considered together in the tax paid that remains after the dwelling house. This simplification should not be a problem since second homes are basically subjected to the same taxation, independently on their number.
4.
The small difference depends on the sequence of the phases of the model. Indeed, the imputation of cadastral value precedes the sample weights calibration.
5.
The data of Dipartimento delle Finanze and Agenzia del Territorio (2012) is a projection.
6.
Actually in 2012 the cadastral value of the dwelling house is not included in gross income so it does not be deducted.
7.
The imputation is made for each taxpayer, so in our model the number of taxpayers with positive gross income is equal to the number of taxpayers with positive taxable income.
8.
Consequently, each taxpayer has a positive tax credit.
9.
Results for each Italian Region can be found in appendix (Tables A.1 and A.2).
10.
The comparison on the average value of gross income by gross income classes can be found in appendix (Figure A.1).
11.
The problem is detected also in Di Nicola et al. (2015). They can recover the small amounts of income within PIT and real estate datasets.
12.
The average value of PIT by gross income classes can be found in appendix (Figure A.2).
13.
Gastaldi et al. (2014) evaluate some VAT reforms on the integrated database built in Pisani and Tedeschi (2014).
14.
Tax base and tax revenue for each Region is reported in appendix (Table A.3). In appendix it is also shown the distribution of tax revenue by income and expenditure deciles (Figure A.3).
15.
Table 10 “Imposte indirette prelevate dalle Amministrazioni pubbliche e dall'Unione europea per tipo di tributo. Anni 1995 - 2015 (milioni di euro correnti)”.
16.
See Bianchini et al.(2013) for a previous application.
17.
The education module can be easily extended to the rest of Italy. For health data are available only for Tuscany.
18.
Data are taken from Comitato Nazionale di Valutazione del Sistema Universitario (CNVSU).
19.
The services for which regional data are available do not cover the entire public health expenditure. Prevention, homecare, assistance against addiction, mental health assistance, primary and district care are excluded.
20.
Sonedda and Turati (2005) find a regressive but weak and not highly significant impact of health expenditure. They follows the insurance value approach.
Appendix
Validation of the model - income year 2012 (billion euro).
| Gross income | Deductions | Taxable income | Gross PIT | |||||
|---|---|---|---|---|---|---|---|---|
| Micro Reg | MEF | Micro Reg | MEF | Micro Reg | MEF | Micro Reg | MEF | |
| Piedmont | 67.5 | 66.8 | 2.0 | 2.1 | 65.5 | 64.4 | 17.5 | 17.3 |
| Aosta valley | 2.1 | 2.1 | 0.1 | 0.1 | 2.1 | 2.0 | 0.6 | 0.5 |
| Lombardy | 164.5 | 163.6 | 5.0 | 5.1 | 159.5 | 157.6 | 44.0 | 44.0 |
| Liguria | 23.8 | 25.1 | 0.7 | 0.8 | 23.1 | 24.2 | 6.3 | 6.5 |
| Trento | 8.4 | 8.3 | 0.3 | 0.3 | 8.2 | 8.0 | 2.2 | 2.1 |
| Bolzano | 8.5 | 8.8 | 0.3 | 0.3 | 8.2 | 8.5 | 2.2 | 2.3 |
| Veneto | 69.9 | 71.8 | 2.0 | 2.6 | 67.9 | 69.0 | 18.1 | 18.5 |
| Friuli Venezia Giulia | 18.2 | 19.0 | 0.5 | 0.6 | 17.7 | 18.4 | 4.6 | 4.9 |
| Emilia Romagna | 71.4 | 70.9 | 2.1 | 2.5 | 69.3 | 68.0 | 18.6 | 18.4 |
| Tuscany | 54.1 | 54.4 | 1.6 | 1.8 | 52.5 | 52.3 | 13.8 | 14.0 |
| Umbria | 11.6 | 11.8 | 0.3 | 0.4 | 11.3 | 11.4 | 2.9 | 3.0 |
| Marche | 19.7 | 20.6 | 0.6 | 0.8 | 19.1 | 19.8 | 5.0 | 5.2 |
| Lazio | 84.3 | 83.2 | 2.6 | 1.9 | 81.6 | 80.7 | 22.5 | 22.6 |
| Abruzzo | 14.2 | 15.3 | 0.4 | 0.4 | 13.8 | 14.9 | 3.5 | 3.9 |
| Molise | 3.1 | 3.3 | 0.1 | 0.1 | 3.0 | 3.2 | 0.8 | 0.8 |
| Campania | 49.3 | 50.5 | 1.5 | 1.1 | 47.8 | 49.3 | 12.6 | 12.9 |
| Apulia | 38.2 | 39.0 | 1.1 | 1.0 | 37.0 | 38.1 | 9.3 | 9.8 |
| Basilicata | 5.1 | 5.7 | 0.2 | 0.2 | 4.9 | 5.5 | 1.3 | 1.4 |
| Calabria | 18.4 | 17.0 | 0.6 | 0.4 | 17.8 | 16.7 | 4.6 | 4.2 |
| Sicily | 39.4 | 45.0 | 1.2 | 1.0 | 38.2 | 44.2 | 9.7 | 11.4 |
| Sardinia | 19.2 | 17.9 | 0.6 | 0.5 | 18.7 | 17.5 | 4.9 | 4.5 |
| Total | 790.9 | 800.4 | 23.7 | 24.0 | 767.2 | 773.6 | 205.1 | 208.2 |
-
Source: MicroReg and Ministry of Finance.
Validation of the model - income year 2012 (billion euro).
| Tax credits by income source | Family tax credits | Net PIT | Regional additional income tax | |||||
|---|---|---|---|---|---|---|---|---|
| MicroReg | MEF | MicroReg | MEF | MicroReg | MEF | MicroReg | MEF | |
| Piedmont | 3.2 | 3.2 | 0.8 | 0.7 | 13.3 | 12.9 | 1.0 | 1.0 |
| Aosta valley | 0.1 | 0.1 | 0.0 | 0.0 | 0.4 | 0.4 | 0.0 | 0.0 |
| Lombardy | 7.0 | 6.9 | 1.7 | 1.6 | 34.8 | 34.0 | 2.2 | 2.2 |
| Liguria | 1.2 | 1.2 | 0.2 | 0.2 | 4.8 | 4.9 | 0.3 | 0.3 |
| Trento | 0.4 | 0.4 | 0.1 | 0.1 | 1.7 | 1.5 | 0.1 | 0.1 |
| Bolzano | 0.3 | 0.4 | 0.1 | 0.1 | 1.8 | 1.8 | 0.0 | 0.1 |
| Veneto | 3.5 | 3.6 | 0.9 | 0.9 | 13.5 | 13.5 | 0.8 | 0.8 |
| Friuli Venezia Giulia | 0.9 | 1.0 | 0.2 | 0.2 | 3.5 | 3.6 | 0.2 | 0.2 |
| Emilia Romagna | 3.3 | 3.4 | 0.7 | 0.7 | 14.4 | 13.7 | 1.1 | 1.1 |
| Tuscany | 2.7 | 2.8 | 0.7 | 0.6 | 10.3 | 10.3 | 0.6 | 0.6 |
| Umbria | 0.7 | 0.7 | 0.1 | 0.2 | 2.0 | 2.1 | 0.1 | 0.1 |
| Marche | 1.2 | 1.2 | 0.3 | 0.3 | 3.5 | 3.6 | 0.2 | 0.3 |
| Lazio | 3.9 | 3.6 | 1.1 | 1.0 | 17.4 | 17.6 | 1.3 | 1.3 |
| Abruzzo | 1.0 | 1.0 | 0.3 | 0.3 | 2.3 | 2.6 | 0.2 | 0.2 |
| Molise | 0.2 | 0.2 | 0.1 | 0.1 | 0.5 | 0.5 | 0.1 | 0.1 |
| Campania | 3.3 | 3.2 | 1.9 | 1.4 | 8.2 | 8.6 | 0.9 | 0.9 |
| Apulia | 2.6 | 2.7 | 1.1 | 1.0 | 5.9 | 6.3 | 0.5 | 0.5 |
| Basilicata | 0.4 | 0.4 | 0.2 | 0.1 | 0.8 | 0.9 | 0.1 | 0.1 |
| Calabria | 1.4 | 1.4 | 0.4 | 0.4 | 2.9 | 2.7 | 0.3 | 0.3 |
| Sicily | 3.0 | 3.1 | 1.5 | 1.2 | 5.8 | 7.5 | 0.6 | 0.7 |
| Sardinia | 1.1 | 1.1 | 0.4 | 0.3 | 3.4 | 3.1 | 0.2 | 0.2 |
| Total | 41.5 | 41.6 | 12.8 | 11.5 | 151.3 | 152.3 | 11.0 | 11.0 |
-
Source: MicroReg and Ministry of Finance.
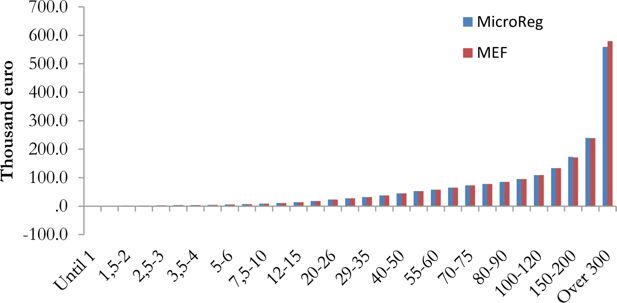
Average value of gross income by gross income classes - income year 2012.
Source: MicroReg and Ministry of Finance.
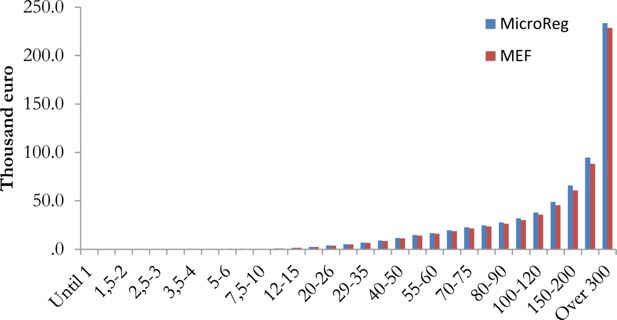
Average value of PIT by gross income classes - income year 2012.
Source: MicroReg and Ministry of Finance.
VAT tax base and revenue (billion euro).
| Tax base | Tax revenue | |||||||
|---|---|---|---|---|---|---|---|---|
| Region/VAT rate | 4% | 10% | 22% | Total | 4% | 10% | 22% | Total |
| Piedmont | 6.5 | 14.1 | 13.7 | 34.3 | 0.3 | 1.4 | 3.0 | 4.7 |
| Aosta valley | 0.2 | 0.4 | 0.4 | 1.0 | 0.0 | 0.0 | 0.1 | 0.1 |
| Lombardy | 14.5 | 32.2 | 33.7 | 80.4 | 0.6 | 3.2 | 7.4 | 11.2 |
| Bolzano | 0.7 | 1.5 | 1.8 | 4.0 | 0.0 | 0.1 | 0.4 | 0.6 |
| Trento | 0.7 | 1.6 | 1.7 | 4.0 | 0.0 | 0.2 | 0.4 | 0.6 |
| Veneto | 6.2 | 14.3 | 15.6 | 36.1 | 0.2 | 1.4 | 3.4 | 5.1 |
| Friuli Venezia Giulia | 1.7 | 3.8 | 4.2 | 9.6 | 0.1 | 0.4 | 0.9 | 1.4 |
| Liguria | 2.4 | 5.1 | 5.1 | 12.6 | 0.1 | 0.5 | 1.1 | 1.7 |
| Emilia Romagna | 5.8 | 13.9 | 15.1 | 34.8 | 0.2 | 1.4 | 3.3 | 4.9 |
| Tuscany | 5.2 | 10.9 | 11.8 | 27.9 | 0.2 | 1.1 | 2.6 | 3.9 |
| Umbria | 1.2 | 2.4 | 2.6 | 6.2 | 0.0 | 0.2 | 0.6 | 0.9 |
| Marche | 2.0 | 4.1 | 4.3 | 10.3 | 0.1 | 0.4 | 0.9 | 1.4 |
| Lazio | 8.0 | 17.1 | 19.1 | 44.2 | 0.3 | 1.7 | 4.2 | 6.2 |
| Abruzzo | 1.6 | 3.3 | 3.5 | 8.3 | 0.1 | 0.3 | 0.8 | 1.2 |
| Molise | 0.4 | 0.8 | 0.7 | 1.8 | 0.0 | 0.1 | 0.2 | 0.2 |
| Campania | 6.0 | 11.9 | 11.6 | 29.5 | 0.2 | 1.2 | 2.5 | 4.0 |
| Apulia | 4.5 | 9.0 | 8.8 | 22.2 | 0.2 | 0.9 | 1.9 | 3.0 |
| Basilicata | 0.6 | 1.3 | 1.3 | 3.2 | 0.0 | 0.1 | 0.3 | 0.4 |
| Calabria | 2.3 | 4.5 | 4.5 | 11.3 | 0.1 | 0.4 | 1.0 | 1.5 |
| Sicily | 5.6 | 10.6 | 10.4 | 26.6 | 0.2 | 1.1 | 2.3 | 3.6 |
| Sardinia | 2.1 | 4.1 | 4.3 | 10.5 | 0.1 | 0.4 | 0.9 | 1.4 |
| Total | 77.9 | 166.8 | 174.2 | 418.8 | 3.1 | 16.7 | 38.3 | 58.1 |
-
Source: MicroReg.
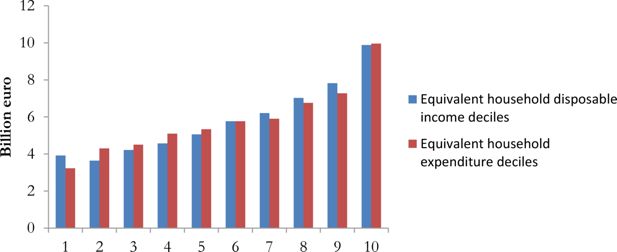
Distribution of VAT revenue by disposable income and expenditure deciles.
Source: MicroReg.
Test t for mean difference — EU-SILC vs HBS — Centre of Italy.
| EU-SILC | HBS | |||||||
|---|---|---|---|---|---|---|---|---|
| Variable | Mean | Standard Deviation | Min | Max | Mean | Standard Deviation | Min | Max |
| Number of rooms | 3.4 | 36.15 | 1 | 6 | 4.26 | 40.08 | 1 | 6 |
| Loan | 0.16 | 12.28 | 0 | 1 | 0.17 | 12.84 | 0 | 1 |
| Number of members | 2.28 | 39.82 | 1 | 5 | 2.25 | 40.29 | 1 | 6 |
| Pc | 0.61 | 16.36 | 0 | 1 | 0.64 | 16.3 | 0 | 1 |
| Internet | 0.57 | 16.62 | 0 | 1 | 0.59 | 16.73 | 0 | 1 |
| Car | 0.81 | 13.24 | 0 | 1 | 0.83 | 12.72 | 0 | 1 |
| Dishwasher | 0.51 | 16.77 | 0 | 1 | 0.61 | 16.59 | 0 | 1 |
| Expenditure | 23,850 | 363,619 | 7303 | 185,488 | 26,369 | 721,718 | 2,657 | 321,923 |
| Number of members <5 years old | 0.14 | 13.37 | 0 | 3 | 0.11 | 12.42 | 0 | 3 |
| Number of members 617 years old | 0.25 | 19.67 | 0 | 4 | 0.26 | 20.1 | 0 | 4 |
| Number of members 1824 years old | 0.15 | 14.31 | 0 | 3 | 0.14 | 13.57 | 0 | 3 |
| Number of members 3469 years old | 1.12 | 28.42 | 0 | 4 | 1.18 | 27.91 | 0 | 4 |
| Householder with low education | 0.52 | 16.77 | 0 | 1 | 0.51 | 16.99 | 0 | 1 |
| Number of managers | 0.02 | 4.9 | 0 | 2 | 0.03 | 6.57 | 0 | 3 |
| Number of self-employed | 0.05 | 7.87 | 0 | 3 | 0.08 | 10.53 | 0 | 3 |
| In property | 0.86 | 11.79 | 0 | 1 | 0.85 | 12.02 | 0 | 1 |
| Number of earners | 1.39 | 26.58 | 0 | 5 | 1.44 | 25.5 | 0 | 5 |
| P-value | 0.9439473 | |||||||
-
Source: our elaborations on HBS and EU-SILC.
Test X2 for equality of distribution - EU-SILC vs. HBS.
| EU-SILC | HBS | |||
|---|---|---|---|---|
| Geographical area | N° | % | N° | % |
| North West | 7,251,965 | 28.3 | 7,270,064 | 28.34 |
| North East | 5,068,067 | 19.78 | 5,055,184 | 19.71 |
| Centre | 5,280,629 | 20.61 | 5,241,862 | 20.44 |
| South | 8,023,134 | 31.31 | 8,083,272 | 31.51 |
| P-value | 1 | |||
| EU-SILC | HBS | |||
| Number of components | N° | % | N° | % |
| 1 | 8,281,042 | 32.32 | 8,391,562 | 32.715 |
| 2 | 6,762,685 | 26.39 | 6,801,077 | 26.515 |
| 3 | 5,045,371 | 19.69 | 4,841,819 | 18.876 |
| 4 | 4,226,780 | 16.5 | 4,331,686 | 16.887 |
| 5 | 1,028,286 | 4.01 | 1,023,989 | 3.992 |
| 6 | 202,530 | 0.79 | 199,543 | 0.778 |
| 7 | 52,711 | 0.21 | 45,463 | 0.177 |
| 8 | 15,078 | 0.06 | 13,698 | 0.053 |
| 9 | 6,810 | 0.03 | 1,249 | 0.005 |
| 10 | 2,410 | 0.01 | 296 | 0.001 |
| P-value | 1 | |||
| EU-SILC | HBS | |||
| Number of earners | N° | % | N° | % |
| 0 | 3,956,170 | 15.44 | 2,506,273 | 9.95 |
| 1 | 13,124,349 | 51.22 | 13,378,643 | 53.13 |
| 2 | 7,109,135 | 27.74 | 8,125,715 | 32.27 |
| 3 | 1,197,490 | 4.67 | 1,009,751 | 4.01 |
| 4 | 215,988 | 0.84 | 148,021 | 0.59 |
| 5 | 20,662 | 0.08 | 13,492 | 0.05 |
| P-value | 0.554 | |||
| EU-SILC | HBS | |||
| Number of females | N° | % | N° | % |
| 0 | 3,703,284 | 14.45 | 3,868,724 | 15.36 |
| 1 | 14,672,359 | 57.26 | 14,380,843 | 57.11 |
| 2 | 5,418,932 | 21.15 | 5,315,662 | 21.11 |
| 3 | 1,615,631 | 6.31 | 1,426,684 | 5.67 |
| 4 | 191,205 | 0.75 | 171,297 | 0.68 |
| 5 | 17,507 | 0.07 | 18,684 | 0.07 |
| 6 | 4,183 | 0.02 | n/a or 0 ? | n/a or 0 ? |
| 7 | 693 | 0 | n/a or 0 ? | n/a or 0 ? |
| P-value | 1 | |||
-
Source: Our elaborations on HBS and EU-SILC.
Regression of consumption on households’ characteristics.
| Number of observations | 19,988 | |||||
| R squared | 0.366 | |||||
| R- squared corr. | 0.365 | |||||
| Variable | DF | Parameter estimate | Standard Error | T statistic | Pr > |t| | Vif |
| Intercept | 1 | 9.08 | 0.02 | 483.94 | <.0001 | 0 |
| Number of rooms | 1 | 0.04 | 0 | 10.78 | <.0001 | 1.26 |
| In property | 1 | -0.26 | 0.01 | -22.41 | <.0001 | 1.17 |
| VHS | 1 | 0.08 | 0.01 | 9.54 | <.0001 | 1.14 |
| Loan | 1 | 0.11 | 0.01 | 8.43 | <.0001 | 1.14 |
| Box | 1 | 0.13 | 0.01 | 14.37 | <.0001 | 1.22 |
| Pc | 1 | 0.14 | 0.02 | 8.9 | <.0001 | 4.15 |
| Car | 1 | 0.27 | 0.01 | 23.11 | <.0001 | 1.51 |
| Internet | 1 | 0.09 | 0.02 | 5.7 | <.0001 | 3.81 |
| Dishwasher | 1 | 0.18 | 0.01 | 19.54 | <.0001 | 1.33 |
| Number of members <5 years old | 1 | 0.03 | 0.01 | 2.49 | 0.013 | 1.22 |
| Number of members 6–17 years old | 1 | 0.03 | 0.01 | 4.26 | <.0001 | 1.56 |
| Number of members 18–24 years old | 1 | 0.05 | 0.01 | 3.93 | <.0001 | 2.41 |
| Number of members 25–34 years old | 1 | -0.01 | 0.01 | -0.74 | 0.461 | 2.19 |
| Number of members 34–69 years old | 1 | 0.03 | 0.01 | 3.93 | <.0001 | 3.03 |
| Householder with low education | 1 | -0.08 | 0.01 | -5.66 | <.0001 | 3.1 |
| Number of males | 1 | 0.02 | 0.01 | 2.91 | 0.004 | 2.46 |
| Number of job seekers | 1 | -0.07 | 0.01 | -5.71 | <.0001 | 2.19 |
| Number of retired | 1 | 0.04 | 0.01 | 4.52 | <.0001 | 2.39 |
| Number of not employed | 1 | 0 | 0.01 | 0.23 | 0.82 | 3.18 |
| Number of managers | 1 | 0.12 | 0.02 | 5.4 | <.0001 | 1.06 |
| Number of self-employed | 1 | 0.08 | 0.01 | 5.22 | <.0001 | 1.1 |
| Number of members with high education | 1 | 0.11 | 0.01 | 10.78 | <.0001 | 2.22 |
| Number of members with medium education | 1 | 0.04 | 0.01 | 4.82 | <.0001 | 3.69 |
| Number of earners | 1 | 0.08 | 0.01 | 7.45 | <.0001 | 4.37 |
-
Source: Our elaborations on HBS.
References
-
1
Fiscal Reforms during Fiscal Consolidation: The Case of ItalyFinanzArchiv: Public Finance Analysis 68:445–465.
-
2
Gli effetti distributivi dei trasferimenti in-kind: il caso dei servizi educativi e sanitariIn: A Brandolini, C Saraceno, editors. Povertá e benessere. Una geografia delle disuguaglianze in Italia. Bologna: Il Mulino. pp. 411–422.
-
3
La SAM come strumento di integrazione e analisiRivista di statistica ufficiale 2-3:35–62.
-
4
A che cosa servono i modelli di microsimulazione? Tre applicazioni usando microRegScience Regionali 2:101–119.
-
5
Federalismo fiscale e redistribuzione: l’ejfetto distributīvo dei benefici in-kind a livello regionale.Un’applicazione a due Regioni italiane, IRPET.
- 6
-
7
Comparative Analysis of Different Techniques to Impute Expenditures into an Income Data SetComparative Analysis of Different Techniques to Impute Expenditures into an Income Data Set, Project no: 028412, AIM-AP Accurate Income Measurement for the Assessment of Public Policies.
-
8
The static microsimulation model of the Italian Department of Finance: Structure and first results regarding income and housing taxationEconomia pubblica.
-
9
Gli immobili in Italia 2012 - Ricchezza, reddito e fiscalitá immobiliareGli immobili in Italia 2012 - Ricchezza, reddito e fiscalitá immobiliare.
-
10
Asimmetrie territorial! nel gap IVA, Atti della Conferenza XXIV SIEP “Economia informale, evasione fiscale e corruzione”Universitá di Pavia, SIEP.
- 11
- 12
-
13
Public health transfers in kind: measuring the distributional effects in Italy, Universitá Commerciale Luigi Bocconi, Econpubblica Centre for Research on the Public Sector, Working Paper, (145)Public health transfers in kind: measuring the distributional effects in Italy, Universitá Commerciale Luigi Bocconi, Econpubblica Centre for Research on the Public Sector, Working Paper, (145).
-
14
Imputation of gross amounts from net incomes in household surveys: an application using EUROMOD. EUROMOD Working Paper EM1/01Imputation of gross amounts from net incomes in household surveys: an application using EUROMOD. EUROMOD Working Paper EM1/01.
-
15
Sintesi dei conti ed aggregati economici delle Amministrazioni pubblicheSintesi dei conti ed aggregati economici delle Amministrazioni pubbliche.
-
16
Il modelh di microsimulazione fiscale dell’IRPET MicroregIl modelh di microsimulazione fiscale dell’IRPET Microreg, IRPET 5/08-ebook.
-
17
Modelling the Redistributive Impact of Indirect Taxes in Europe: An Application of Eurmod. EUROMOD Working Paper no. EM7/01Modelling the Redistributive Impact of Indirect Taxes in Europe: An Application of Eurmod. EUROMOD Working Paper no. EM7/01.
-
18
Developing a static microsimulation model for the analysis of housing taxation in ItalyInternational Journal of Microsimulation 4:73–85.
-
19
Micro Data Fusion of Italian Expenditures and Incomes Surveys. WP n.164, Working Papers Series of the Department of Public Economics - Sapienza University of RomeMicro Data Fusion of Italian Expenditures and Incomes Surveys. WP n.164, Working Papers Series of the Department of Public Economics - Sapienza University of Rome.
-
20
Winners and losers in the Italian Welfare State: A microsimulation analysis of income redistribution considering in-kind transfersGiornale degli Economisti 64:423–464.
-
21
Final report EUROMOD: An Integrated European Benefit Tax Model. Working Paper, n. EM9Final report EUROMOD: An Integrated European Benefit Tax Model. Working Paper, n. EM9.
-
22
The tax shift from labor to consumption in Italy: afiscal microsimulation analysis using EUROMODUniversity of Genoa.
Article and author information
Author details
Publication history
- Version of Record published: April 30, 2017 (version 1)
Copyright
© 2017, Maitino
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

