Life time pension benefits relative to life time contributions
Abstract
By extending a dynamic micro simulation model we compare total expected discounted contributions to the Norwegian National Insurance System with expected discounted sum of benefits from pensions received for cohorts born between 1910 and 2070. The results show that the cohorts, who established the pay-as-you-go system in 1967, experienced a substantial gain by letting future generations pay. As a result of the pension reform from 2011 future pension benefits will be tightened. With a positive net rate of interest cohorts born between 1950 and 1980 are those who are most hurt by the reform, while cohorts born after 2000 gain.
1. Introduction
Insurance against drop in incomes and redistribution are two main objectives for a public pension system. Securing of incomes after retirement from working life and insurance against the consequences of getting disabled before retirement age are probably two of the most important elements. A public pension system financed pay-as-you-go normally will redistribute incomes within and between generations. Emphasis in this paper is put on distribution between generations caused by the public pension system in Norway. As pointed out by Feldstein and Liebman (2002) mapping of distributional effects is an important element in an overall discussion of the trade-off between protection and distortion when designing a pension system. Especially, it has been important in the discussion around the Norwegian pension reform from 2011.
Over the life course members of an insurance system normally will contribute by payments when in working age, and later receive pension benefits as disabled or old-age pensioners. To obtain an overall view of distributional effects of the pension system between different birth cohorts, it is relevant to compare expected discounted pension contributions from labour market earnings for each cohort over the life course with discounted sum of pension benefits each cohort is expected to receive. If the size of the different cohorts is roughly constant, pension expenditures in a matured system also stay rather constant. When pension expenditures are financed pay-as-you-go there also has to be a close correspondence between contributions paid and benefits received for each cohort. But the first cohorts covered with benefits from a pay-as-you go pension system normally will receive higher benefits than what follows from their contributions. Reforms of the pension system may also affect the ratio between discounted life time pension benefits and discounted life time contributions. With population growth, it may be possible to let the sum of benefits each generation receives be higher than their contribution.
A calculation of actual contributions to the insurance scheme over the working period for a generation with the aim to compare with actual sum of pension benefits, demands data that are hardly available in any country. And more important, actual calculations for each generation are not possible until the last member of this generation is dead. Projected values based on realistic assumptions have to be used. The comprehensive need for a lot of details from past and future data is a major reason why there are few examples of this kind of analyses in the economic literature. Generational Accounts based on methods developed by Auerbach, Gokhale, and Kotlikoff (1991) is one of the most common methods used to analyse distributional consequences between different generations from given levels of government revenues and expenditures. A recent analysis for the Netherlands is published by Bettendorf et al. (2011) incorporating generational accounts in a model with overlapping generations. Like in Miles and Iben (2000), stylized models with overlapping generations are also used in the literature to show which generations might be gainers, and which losers, from a transition from an unfunded to a funded state pension system.
While the purpose of Generational Accounts is to decide whether the design of a welfare system is in accordance with fiscal sustainability in the long run, the aim of our analysis is to illuminate effects from the Norwegian pension system on distribution of income between birth cohorts from 1910 to 2070. For this purpose we extend Statistics Norway’s dynamic micro simulation model MOSART, documented by Fredriksen (1998). The method used corresponds to an analysis of lifetime income redistribution for old-age state pensions in the Netherlands by Nelissen (1995) and an analysis of redistribution between generations caused by the design of the Swedish Welfare State published in Pettersson, Pettersson, and Westerberg (2006).
In line with recommendations from Orcutt, Merz, and Quinke (1986) we use a dynamic micro simulation model to capture the heterogeneity of the population in combination with rather complicated pension benefit rules. Wolfson (1979) was the first who looked at lifetime incidence of a social security scheme by using this kind of model. Creedy, Disney, and Whitehouse (1993) also use a micro simulation model to analyse the lifetime redistribution of the earnings-related state pension in the UK. By micro simulation it is possible to take into consideration that different parts of the population face different rules. Substantial problems of aggregation to calculate effects on government budgets and to analyse overall distributional effects are rather easily handled. The main strength of micro simulation is to represent a socioeconomic system by a sample of decision units and then model different events, which these units may be exposed to. Contrary to what is possible in a macroeconomic approach, detailed and complicated tax and benefit rules may be exactly reproduced. However, it is rather costly to establish a detailed microsimulation model, and access to administrative data for the events covered is necessary. Using a representative aging approach by i.e. birth cohort, gender and occupational characteristics as in Belloni and Maccheroni (2013), may therefore be a good approximation even though it is impossible to include as many details by this approach as possible with microsimulation.
Like in Wolfson (1979) the focus in the analyses by Creedy et al. (1993), Nelissen (1998), Cornado, Fullerton, and Glass (2000), Gustman and Steinmeier (2001) and Liebman (2002) is on distributional effects from the social security system on life cycle incomes for persons within specific cohorts. The focus in this paper is more congruent with Nelissen (1995) comparing effects from the social security system on redistribution of life cycle incomes between different cohorts. Although a main emphasis in Nelissen (1995) is on redistribution in lifetime incomes within cohorts, he also looks at changes in redistribution between cohorts born in 1930, 1940, 1950 and 1960, respectively. Pettersson et al. (2006) focus on intergenerational effects by using the Swedish dynamic micro simulation model SESIM in their analyses of distributional effects from major government incomes and expenditures for generations born between 1930 and 2009. The aim of our paper has mainly been to evaluate redistributive effects of net benefits over the life-cycle between different birth cohorts from the reform of the pension system in 2011. The reform changed the original Defined Benefit (DB) system towards Notional Defined Contributions (NDC) in a corresponding way as earlier reforms in Italy, Latvia, Poland and Sweden, cf. Dominczak, Franco, and Palmer (2012).
The MOSART model is especially designed to analyse budgetary and distributional effects from different designs of the Norwegian National Insurance System (NIS), and the model has been used during the past two decades to analyse budgetary and distributional effects from the implementation of the new pension system. However, main concern regarding distributional effects of the reform in the former analyses has been on horizontal effects for old-age pensioners in a future year, e.g. 2060 cf. Christensen, Fredriksen, Lien, and Stølen (2012). In 2060 a major part of the old-age pensioners receives their benefits based on the rules from the new system. In this paper the model and the calculations have been extended as discussed in Section 4 to compare effects over the life cycle for all cohorts born between 1910 and 2070.
2. The dynamic micro simulation model mosart
Based on detailed information for the population in a base year, the MOSART model simulates the further life course for each individual of the Norwegian population. The simulations are made by possible transitions from one state to another, given by transition probabilities depending on each person’s characteristics. Transition probabilities are estimated from observed transitions in a recent period. Events included in the simulation are migration, deaths, births, marriages, divorces, educational activities, retirements and labour force participation. Public pension benefits are calculated from labour market earnings and other characteristics.
The model is based on discrete time with calendar year as time unit. Normally simulations are based on detailed information for the population from a recent year. To compare total discounted contributions to the Norwegian NIS over the life course with expected discounted sum of benefits for as many birth cohorts as possible encompassed by the system from 1967, the backward limit is fixed by the possibility to construct a synthetic base year population. Based on detailed information from the Norwegian Population Census, available aggregated data from 1960 is the earliest possible starting point for the simulation. As further discussed in Section 4.1, this makes it possible, with some weaknesses for the first cohorts, to compare total discounted contributions over the life course with expected discounted sum of benefits for every cohort since 1910.
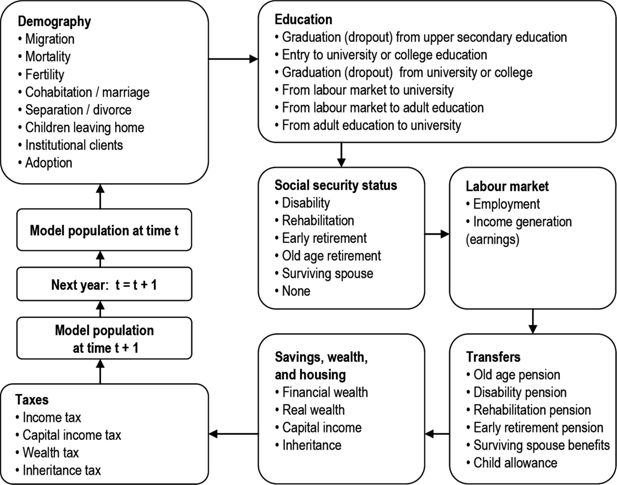
The main structure of the MOSART model is presented in Figure 1. The model simulates the whole population each year before entering the next (cross-sectional simulation), rather than handling the full life course of each person before dealing with the next person (longitudinal simulation). Cross-sectional simulation requires more computer resources in the form of internal memory, but increases the possibilities for interaction between individuals in the model population (e.g. marriage) and for adjusting the transition probabilities against external restrictions (e.g. changing fertility). The model also simulates each event for the whole population before simulating the next event.
The simulations in the model start with the demographic events. These events and the underlying demographic assumptions are to a large degree based on the official population projections from Statistics Norway, (see Statistics Norway, 2016). For the present analysis the assumptions are based on the medium alternative of Statistics Norway’s demographic projections from June 2012. A total fertility rate of 1.87 and net immigration shrinking from the existing level of more than 40,000 persons towards 10,000–15,000 persons per year in the long run imply a continual growth in the younger part of the population in the first decades. But especially the number of elderly will show a significant growth in the first decades as a result of the larger cohorts born after the Second World War and expected growth in remaining life expectancy at the age of 62 for about 4 years from 2011 to 2050.
The level of education is of significant importance for performance in the labour market both regarding labour market participation and labour incomes. It is also evident that persons with low education have a significant higher propensity for getting disabled and retire early compared to persons with high education. Persons with low education also have significant lower remaining life expectancy than persons with high education. Even though it may be discussed if there is causality between education and other events, the level of education is of significant importance for transitions in the labour market and the probabilities for entering into disability, early retirement and death in the MOSART model. In the development of the model, heavy weight is therefore put on modelling of educational activities and examinations for each person depending on gender, age and last year’s attainment, see Gjefsen (2013). In the model individuals’ paths through the educational system are determined by the following choices: whether to start an educational activity; choice of level and field of education; whether to continue or not; and finally whether to fulfil or not.
The labour market block simulates size and composition of labour force and man-years as well as labour market incomes. In general total labour force and man-years in MOSART are projected by assuming constant participation rates and working hours by gender, age, number of children, educational activity, level of education completed and retirement. There are no dynamics in participation rates and working hours, i.e. they are independent of former observations. However, the pension reform from 2011 is expected to have a significant effect on participation rates, especially for the elderly, and some effect on working hours for the entire labour force. These effects are discussed in more detail in Section 4.2.
Labour market incomes are simulated to be in accordance with the number of man-years. The composition of labour market incomes depends on the same characteristics as man-years mentioned above. Additionally, dynamics are included taking into account that unstable labour market participation from the past may cause unstable participation in the future, especially among men.
Retirement from labour market participation to status as a pensioner is one of the most important transitions included in the model. These transitions and the implications for government budgets are highly dependent on the design of the pension system described in Section 3. Effects from the pension reform on retirement and labour supply are discussed in Section 4.2, while effects on contribution rates are discussed in Section 4.3.
Because pension expenditures in Norway mainly are financed via government incomes in general and not via specific contributions, details in the tax system are of minor importance for the analyses of distributional consequences between different cohorts. As further discussed in Section 4.3, we for simplicity assume that increasing pension expenditures have been, and will be, met by a proportional increase in average taxes connected to labour market incomes. Because a major part of household savings in Norway is in houses and dwellings due to tax favouritism, it has also been difficult so far to detect important effects from the pension reform on savings behaviour.
3. Design of the norwegian pension system
3.1 Main pillars
Like in many other countries the pension system in Norway may be said to be built on three pillars:
The National Insurance System (NIS)
Occupational pensions including early retirement schemes
Private savings for future pensions
Contrary to many other countries, the NIS established in 1967 and covering the entire population, is the most important pillar. In 2014 cash benefits from the Central Government to households from the long-term arrangements in NIS (old-age pensions, disability pensions and survivors’ pensions) amounted to about 11 per cent of Gross Domestic product (GDP) for Mainland Norway.
The NIS in Norway is an integrated part of the Central Government budget and financed pay-as-you-go. Contrary to many other countries with more funded systems, NIS is not autonomous, and the yearly expenditures have not to be balanced by specific contributions. General tax revenues cover pension expenditures.
Occupational pensions in the Central and Local Government sector and a general old-age pension system existed before NIS was established in 1967. Since then, old-age, disability and survivors’ benefits from the Central and Local Government occupational pensions have been coordinated with the corresponding benefits from NIS, giving a total level slightly above what follows from the Government occupational pensions alone.
In the private sector there have been huge variations in the occupational pension schemes with respect to benefit levels, duration of benefits, indexation, and whether the schemes have been defined benefit or defined contribution. Before 2006 each company could choose whether or not to offer supplementary pensions to its employees, and many companies did not provide any occupational pension at all. In general benefits from occupational pensions in the private sector have been significantly less generous than the corresponding benefits in the Government sector. Occupational benefits in the private sector may be characterized as supplementary and are usually not coordinated with NIS. In 2006 a minimum level of supplementary pensions was made mandatory by law for all employees, and companies must at least pay 2 per cent of wages exceeding 1 basic pension unit (BPU) into a Defined Contribution (DC) pension scheme.
Between 1973 and 2010 the retirement age for old-age pension benefits in NIS was 67 years. To allow ‘tired’ workers to retire before the age of 67 without using the disability pension scheme, an early retirement scheme (AFP) was introduced in 1989 as a result from a tripartite agreement between the Norwegian Confederation of Trade Unions (LO), the Confederation of Norwegian Enterprises (NHO) and the Norwegian Government in 1988. By this agreement it became possible for wage earners in the private sector covered by the scheme to retire at the age of 66. The scheme was gradually spread to other collectively agreements including the Government sector, and the earliest possible retirement age was gradually reduced to the age of 62. All employees in the Government sector and about 60 per cent of the employees in the private sector are covered by the agreement. Before the reform of the system for old-age pensions in NIS in 2011, early retirement was possible with hardly any consequences for future benefits from NIS after the age of 67.
The early retirement scheme in the private sector was included and adapted to the new old-age pension scheme in NIS as a part of the pension reform in 2011. In the Government sector only a partial agreement was reached between the trade unions and the Government during negotiations in 2009 on how to adopt the former early retirement scheme to the new system. As a consequence means-testing of benefits from the early retirement scheme against labour incomes between the ages of 62 and 67 is maintained in the Public sector, and retirement before 67 is of minor consequence for old-age benefits after the age of 67.
Private savings in pension schemes has not been very usual in Norway. Due to tax-favouritism, savings in houses and dwellings has been the most popular way of private savings. In 2014, 67 per cent of households’ gross wealth was in houses and dwellings, and the capital is estimated to be more than twice GDP for Mainland-Norway. The value of bank deposits amounted to 13 per cent of households’ total gross wealth, while households’ holdings of shares and other securities amounted to above 10 per cent.
3.2 Public old age pensions
The system for old-age pensions in NIS is a non-autonomous part of Central Government budgets and financed pay-as-you-go. While the former system from 1967 was based on Defined Benefits, the system from 2011 is more actuarial and may be characterized as NDC, see Christensen et al. (2012) for more details. With the old system, retirement for old-age pensions was restricted to the age between 67 and 70. With the new system, old-age pensions may be drawn partly or completely between the age of 62 and 75. Contrary to the old system, work and pensions may also be freely combined without any earnings test.
While annual benefits with the old system were independent of the age of retirement, annual benefits with the new system are calculated by dividing accumulated entitlements by expected years as retired. The level of benefits with the new system before remaining life expectancy is taken into account is however calibrated to the level of benefits with the old system. This means that divisors for adjusting for retirement age and remaining life expectancy for each cohort are calibrated against the divisors for persons born in 1943 retiring at age 67 in 2010. Early retirement thus leads to lower annual benefits. Lower benefits caused by higher life expectancy may be counteracted by postponing retirement. Statistical observations for the first years after the reform and econometric analyses based on these observations by Hernæs, Markussen, Piggott, and Roed (2016) already show that the reform has led to postponed retirement (in the sense working longer).
The new system also means a closer connection between pension entitlements and former labour incomes. Between ages 13 and 75 entitlements for old age pensions in the new system are accumulated by 18.1 per cent of annual labour incomes up to a ceiling of 7.1 times the BPU. BPU is a measurement unit in the National Insurance Scheme corresponding to about 1/6 of the average annual wage level for a full time employee. The ceiling thus corresponds to approximately 120 per cent of the average wage level.
The main changes to obtain greater correspondence between pension entitlements and former labour incomes compared to the old system are:
Accumulation of entitlements from the first income earned against 1 BPU with the old system.
A maximum of 40 years of entitlements in the old system is abolished.
A rule for accumulation of entitlements based on the 20 years with highest incomes is also abolished.
Compared to the ceiling of 7.1 BPU for earning of entitlements with the new system, full accumulation of entitlements in the old system took place up to 6 BPU with a slanting roof of 1/3 between 6 and 12 BPU.
For persons with unpaid homecare, yearly entitlements were increased from 4 BPU in the old system to 4.5 BPU in the new system. These entitlements are means-tested 100 per cent against labour incomes.
Strong elements of redistribution in the Norwegian pension system compared to most other countries are maintained with the new system. A guarantee pension of 2 BPU for singles and 1.9 BPU per person for couples secures a minimum level of benefits for pensioners with low labour incomes. The guarantee pension is means-tested with 80 per cent against income entitlements, and even persons with small incomes will obtain a level of pension benefits somewhat higher than the minimum level as shown in Figure 2. In this figure the connection between annual pension benefits and former labour incomes is shown with the new and the old system for a single person with constant labour incomes during a period of 40 years. Annual benefits are shown before taking life expectancy adjustments into account, and thus represent the system for accumulation of entitlements. A ceiling on annual incomes for full accumulation of entitlements at 7.1 BPU in the new system compared to 6 BPU in the old system means that especially persons in this interval gain from the change in the accumulation model. However, for annual incomes between 7.1 and 12 BPU the former connection at the margin between labour incomes and accumulation of entitlements is eliminated. More comprehensive analyses documenting horizontal distributional effects as a result of the reform in Christensen et al. (2012) reflect the simplified illustration in Figure 2. Adequacy of the new pension system for different levels of income and retirement behaviour is also discussed. Persons with incomes above average gain from the reform, before taking indexing and life expectancy adjustments into account. Persons with low incomes are also positively affected.
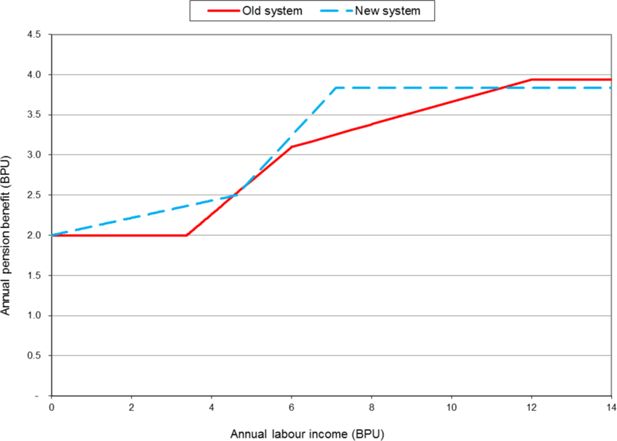
Connection between annual labour incomes and annual pension benefits with old and new pension system.
Notes: For a single person assuming constant labour incomes for 40 years.
The actuarial design with adjustments for changes in life expectancy in combination with flexible retirement over the interval 62–75 years was introduced in 2011. This means that old age pension benefits may be drawn partly or completely from the age of 62, and work and pensions may be freely combined without any earnings test. From accumulated entitlements at retirement age A, WA, annual pension benefits for a cohort K retiring at that age are calculated by dividing by divisors ΦK,A reflecting remaining life expectancy at that age. Calculation of divisors for a cohort is based on average mortality tables for men and women together, and is also independent from level of education.
Here:
Bk,A = Annual pension benefits for persons from cohort K, retiring at age A
WA = Accumulated entitlements at age A, and
ΦK,A = Divisors for persons from cohort K retiring at age A
The actuarial design reflected in Equation 1 says that accumulated entitlements are divided by expected years as retired. Early retirement leads to lower annual benefits because accumulated entitlements have to be divided by more years. This is also the case when life expectancy increases for a given retirement age. Lower benefits, when life expectancy increases, may be counteracted by postponing retirement.
In the new system pension entitlements during accumulation are indexed to wage growth. After retirement income pension in payment is indexed to wages, but subtracted a fixed component of 0.75 per cent per year. The level of the guaranteed pension will be adjusted by growth in wages, but reduced with higher life expectancy. In demographic projections from Statistics Norway, life expectancy at the age of 67 is assumed to increase by approximately 0.5 per cent a year in the long run. Then the indexation of minimum pensions usually will be higher than price indexation.
Persons born in 1953 or earlier will earn their pension entitlements only according to the old system. In the group born from 1954 to 1962 pension entitlements will partly be calculated from the old system and partly from the new with an increasing share. Pension entitlements for persons born in 1954 will be 90 per cent based on the old rules and 10 per cent on the new. Persons born in 1963 or later will earn their pension entitlements completely according to the new system.
3.3 Disability pensions and old age pensions for former disabled
Under the old system disability pension and old-age pension were interconnected, and disability pensioners usually kept their pensions unchanged when they were transferred to old-age pension at age 67. About 11 per cent of the population aged 18–67 is on disability pension, and at age 67 about 40 per cent of the new old-age pensioners are former disabled. As a part of the pension reform, the Government in 2011 proposed a new disability scheme and a new model for calculating old-age pensions for earlier disabled. The new disability scheme is implemented from 2015. With this scheme disability pension is calculated more as a short term benefit with a replacement rate of 66 per cent and taxed like earnings.
Like in the old system, disability pensioners will be transferred to old-age pensions at the age of 67. Because persons receiving disability benefits are not in a position to work after this age to counteract higher life expectancy, the Government decided that reduction in yearly benefits caused by growing life expectancy for a new disabled at age 67 only should be one half of the reduction implemented for former non-disabled retiring at this age. Over time this more lenient life expectancy adjustment for those who are former disabled will increase incentives for getting disabled before obtaining old age pension. By 2018 life expectancy adjustment of old-age pensions for earlier disabled is to be evaluated in light of whether non-disabled compensate for the life expectancy adjustment by working longer.
3.4 Survivors’ pensions
Survivors’ pensions are also still interconnected to the old system for old age pensions. Given some conditions about own incomes and common children, a surviving spouse may get extra pension benefits dependent on accumulated entitlements of the deceased spouse. If the surviving spouse receives old age benefits, she may also get a supplementary survivors’ pension means-tested against her own entitlements for supplementary or income dependent pension. A majority of surviving spouses are women, and normally their personal pension entitlements are significantly lower than the corresponding entitlements of their husbands.
4. Methodological challenges
4.1 Information for every cohort over the life course
Calculation of pension wealth for each individual over the life course for a range of cohorts meets several methodological challenges. Firstly, data for labour market incomes and pension benefits for each person included in the simulation are necessary. The need for future information for the present and future population is simply met by using the MOSART model to simulate further life course for each person, also including new persons by birth or immigration. The same approach is also used by Nelissen (1995) and (1998) and Pettersson et al. (2006). A main problem is caused by lack of data from the first years of working activity for present adults. This problem may be solved in several ways:
We may start the simulation with a synthetic population in an early year (e.g. 1960). This approach is used by Nelissen (1995, 1998). He derives a usable sample from the 1947 Census data, and he is thus able to start his analyses with the cohort from 1930 who mainly accumulates their pension entitlements after 1947. However, it is not documented how information on contributions to the accumulation of entitlements is collected for the first cohorts.
We may try to establish historical data for wages and pension payments for present adults’ early working life, but this data job may demand a lot of resources. This approach is used by Pettersson et al. (2006) by combining macro data for government revenues and expenditures back to 1930 from Statistics Sweden with more or less scattered information on the distribution among individuals with different characteristics.
By only focusing on accumulated gross pension wealth, the analyses could be constrained to those younger than 67 years of age, the formal retirement age with the former pension system.
The analyses could be constrained to focus on effects from the pension reform on gross pension wealth, and compare with expected income over the remaining life course.
To get a most comprehensive picture as possible of distributional effects from the pension system over the life course for different cohorts, we have chosen to follow the approach by Nelissen (1995, 1998) according to suggestion a) above. Based on data from the Norwegian Population Census in 1960, it has been possible to start the simulation based on this population of individuals with characteristics consistent with aggregate information. For the period 1961–2012 transition probabilities in the model are also adjusted in order to make the simulation correspond to observed time series at the aggregate level. All persons living in Norway in 1960, or born or immigrated afterwards, are included in the simulation. This method provides a full set of simulated income data for every person in the grown up population born in 1943 (and thereby 17 years of age in 1960) or later. Simulations from 2010 and onwards are partly based on a prolonging of the system that existed before the reform and partly on the approved pension system.
4.2 Labour supply effects
Labour supply with the new system is expected to be higher than with the former. At the intensive margin (before age of retirement) a closer connection between accumulation of pension entitlements and former labour incomes means an implicit reduction of the marginal tax rate for labour. In Stensnes (2007) this implicit tax reduction is estimated to stimulate labour supply on the intensive margin by 2.5 per cent. It is reasonable to think that both labour market participation rates and average working hours may be affected, and we have assumed that they will increase by 1¼ per cent each. The slight increase in labour supply at the intensive margin also leads to higher accumulation of entitlements and thereby higher pensions.
Like the results from the analyses by Heckman (1993) and Immervoll, Kleven, Kreiner, and Saez (2007) it is reasonable to think that labour supply as a result of the Norwegian pension reform in 2011 is more affected at the extensive margin relative to the intensive. Retirement may be postponed as an immediate effect because of the reform, and further postponed when life expectancy increases. The first comprehensive econometric analyses of immediate effects on retirement by Hernæs et al. (2016) confirm that the reform particularly has caused postponed retirement for employees in the private sector entitled to the early retirement scheme. Because the reform of the pension system for employees in the Public sector in the first round did not turn out to follow the model from the private sector, retirement behaviour for this group does not seem to be much affected. Based on more preliminary considerations Fredriksen and Stølen (2011) calculate the average immediate effect on retirement above 0.2 years while an average worker (included those working in the Public sector) may postpone the retirement age by 0.5 years for each year life expectancy increases. Remaining life expectancy at the age of retirement is expected to increase during the whole period of simulation, but with a slower degree towards the end of the period than in the beginning. As a consequence of the actuarial design of the new system, uncertainty regarding the impact on the sum of future pension benefits is smaller than the effect on retirement age. A small effect on retirement age means a strong reduction in yearly benefits and vice versa.
4.3 Contribution rate
Contrary to the Dutch General Old-Age pension system analysed by Nelissen (1995, 1998), the Norwegian NIS is financed pay-as-you-go. Thus, in the Norwegian system there is no direct connection between taxes and contributions paid and the amount of pension benefits received. Pension contributions and expenditures in NIS are integrated components of the Norwegian government budget. Although payroll taxes and pension premiums on labour incomes are features of the Norwegian tax system that originally were intended to cover total pension expenditures in NIS when the system was introduced in 1967, revenues from these taxes have been far from sufficient. Because the number of old-age pensioners is still low compared to the size of the labour force, the estimated contribution rate for old-age pensions is still much lower than the accrual rate of 18.1 per cent in the new system. Actual costs will probably not correspond to this number before around 2040.
Nevertheless, there are good reasons to say that NIS is financed by its members, and it is possible to produce estimates for how this fiscal burden is distributed. In a pay-as-you-go system in which public pension expenditures are financed by current tax revenues, the so-called average contribution rate defined by Disney (2004, p. 274), may be a simplified measure for each member’s contribution. Disney defined the contribution rate for a public pension scheme as “the average rate (on earnings) that would be required to finance current spending on public pensions without budgetary transfers or the accumulation or decumulation of public pension funds”. Under standard pay-as-you-go formula, the contribution rate (CR) may be calculated as the ratio of public pension payments (PP) to labour incomes (LI). Gross pensions are taxed in Norway, but more lenient than labour incomes, and therefore an appropriate contribution rate in accordance with the Disney definition may formally be calculated as:
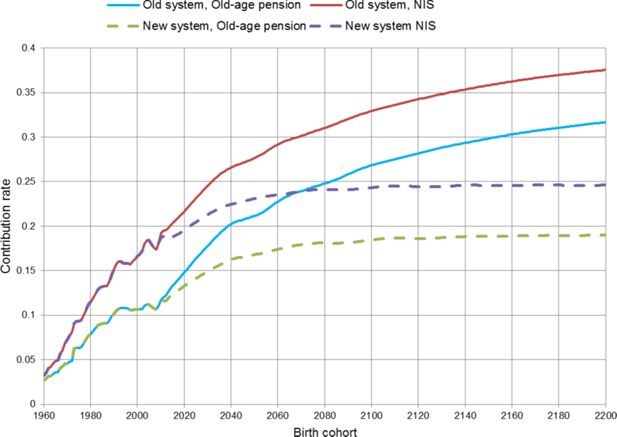
The right hand side numerator represents nominal public pension expenditures, whereas the denominator is the relevant tax base. The parameter γ represents the more lenient taxation of pension incomes compared to wage incomes, and is approximated to about 50 per cent under the current tax regime. The contribution rate can be interpreted as the tax rate sufficient to finance pension expenditures, assuming that the entire tax burden falls on labour and pension incomes. Average contribution rates dependent on pension system and are presented in Figure 3 for old-age benefits, and NIS also including disability benefits and survivors’ benefits.
At the start of the period of simulation in 1960 the average contribution rate for old age pensions in Norway was only 2.6 per cent and 3.2 per cent when also disability and survivors’ pensions were included. At that time retirement age for old-age pensions was 70 years, and because of rather short duration of life, many Norwegians didn’t reach that age. Due to decreasing mortality and larger birth cohorts reaching retirement age, the average contribution rate for old age pension grew steadily from 1960 to 1990, but because of small cohorts born between the two World Wars this contribution rate stayed almost constant about 11 per cent from 1990 to 2010.
Because of large cohorts born after the Second World War and further growth in life expectancy, continuing the old pension system would have meant an almost doubling of the old age pension contribution rate from 2010 to 2050. And the contribution rate would have continued to increase as long as life expectancy was increasing and retirement age was kept constant. Due to the pension reform, growth in average contribution rate for old-age pensions will be smaller. This contribution rate is estimated to reach about 17 per cent in 2050 and stabilize about 19 per cent towards the end of the period of simulation. Further growth in expenditures as a result of increasing life expectancy is counteracted by the new system. But increasing pension expenditures as a result of larger cohorts born after the Second World War compared to the decades before have to be covered by the tax-payers.
4.4 Net rate of interest
A comparison of the present value of contributions to the financing of old age pensions and NIS over the life course for each birth cohort with the present value of pension benefits received, is probably the most appropriate way to calculate each cohort’s net contribution. In calculating present values of contributions and benefits it is necessary to choose a relevant net rate of interest ϱ:
Here:
i = the nominal rate of interest
w = average wage growth
In NIS accumulated entitlements for old age pensions are indexed by wage growth synonymous with the net rate of interest fixed equal to zero. While this assumption is appropriate for indexation of accumulated entitlements in NIS, it is not suitable when comparing present value of contributions with present value of benefits, or in more general analyses of sustainability in public finance. By assuming that the net rate of interest is zero, what happens today is of no importance compared to what happens in the future with an infinite horizon. For example, a weakening of the government budget today may give an advantage to the tax-payers or the users of government services and pension benefits in the short run that is never counteracted in the long run because a deficit in public finances may be pushed to infinity. If the net rate of interest is zero, there will therefore be no budget constraint by this approach. It is not obvious what net rate of interest that should be chosen, and we will show that the results are highly sensitive for the choice. A common practice in Norway, also used by the Ministry of Finance to calculate present values of contributions and benefits in the so called Generational Accounts, has been to assume a net rate of interest of 1.96 per cent corresponding to a yearly growth in real wages of 2 per cent and a real rate of interest of 4 per cent.
In his analyses Nelissen (1995) also chooses a net discount rate of 2 per cent, arguing that this is roughly the real interest rate in the Netherlands during the last hundred years. In the paper from 1998, however, Nelissen uses a real discount rate of 4 per cent in the main alternative and shows the effect of alternative assumptions of 2 and 6 per cent respectively. Coronado et al. (2000) use a discount rate of 2 per cent in the main alternative, but they also show the effects from an interest rate of 4 per cent. On the other hand, Pettersson et al. (2006) do not take any discounting into account in their analyses. They adjust incomes and transfers with inflation and economic growth assuming that the value of contributions and receipts of pension benefits and transfers are independent on when they respectively are paid and received. They argue that individual time preferences and risk aversion should not be taken into account because the analyses intend to show the situation after everyone in a generation is dead. Even though they admit that an amount of money now has to be preferred compared to the same amount later, this argument is met by including capital incomes in the analyses.
4.5 Adjustments for household composition?
In horizontal analyses of distributional effects from different kinds of incomes and transfers over the population, it is common to take into account the composition of households to which the individuals belong. Total incomes received by all members of the household (eventually also taxes and other contributions members of the household pay) are divided between each member by using some equivalence scale. Also for analyses of distribution of life time incomes Coronado et al. (2000) and Gustman and Steinmeier (2000) find it relevant to take the incomes and benefits for the spouse into consideration.
However, it is not quite obvious that household composition should be taken into account in distributional analyses between different cohorts. Most old-age pension systems are based on accumulation of individual rights independent of the household a person belongs to. Only with a few exceptions old-age pension benefits are received independently of the household composition. So in this paper, concentrating on distributional effects between different generations we focus on individual contributions and benefits. Contrary, in their analyses of overall distribution of net effects of all governmental revenues (taxes) and expenditures (benefits), Pettersson et al. (2006) choose to take the household composition into account. They therefore choose to charge the home-living children with a part of all taxes paid by their parents, while the parents receive a part of the children allowances and subsidized kindergartens and education. In his analyses of horizontal distributional effects of the pension system over the life cycle for selected cohorts, Nelissen (1995, 1998) also adjusts the income components for household composition. The pension benefits for couples in the Netherlands seem to be much more integrated than in the Norwegian system.
5. Results
The point of departure for the simulations is every person resident in Norway in 1960, and persons born or immigrated afterwards. Persons born in Norway before 1960, who also have died before that year, are not included in the results presented below. All other persons are included irrespective of how old they were when they died. All amounts are measured in NOK in fixed wages from 2011and are discounted to age 62 for every cohort. As presented below the results are somewhat affected by a rather high net immigration to Norway. In some years after 2010 net immigration has increased to above 40,000 persons per year, corresponding to more than 0.8 per cent of the entire Norwegian population and 70 per cent of a birth cohort. The size of net immigration affects the results because many persons will only have spent a part of their lives as adults in Norway. Therefore several of the figures below are constrained to natives, i.e. persons resident in Norway since the age of 17. In some figures we have shown the difference between natives and immigrants. Due to former weaknesses in registration of education among immigrants, presented figures by level of education are constrained to natives only.
5.1 Gross pension wealth
The first stage in the empirical analysis is to take a look at gross pension wealth, i.e. expected present discounted value of all pension benefits received over the life cycle. This is shown by level of education for the new and old pension system and for old age pensions and the total of old age pensions, disability pensions and survivors’ pensions in Figure 4 and Figure 5 respectively. Although the simulation starts in 1960, it is possible to calculate gross pension wealth for persons born from about 1910. Persons from this generation, who survived until the age for old-age retirement, did not receive old-age pensions before 1977, and their total entitlements were then registered. This is also the case for most of their expected rights for disability pensions, although there may be some weaknesses in estimating these rights when this generation was relatively young.
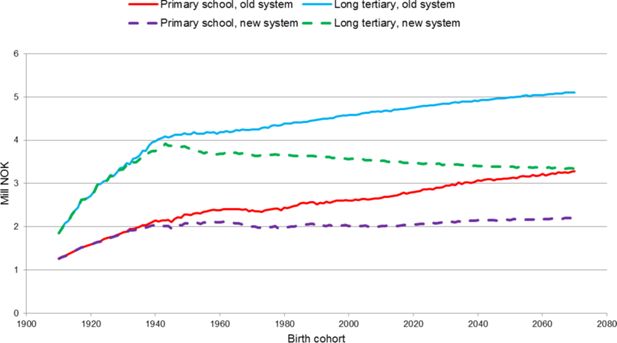
Average discounted gross pension wealth at age 62 by level of education and pension system, old age pensions, net discount rate of 2 per cent. Mill NOK in 2011 amounts.
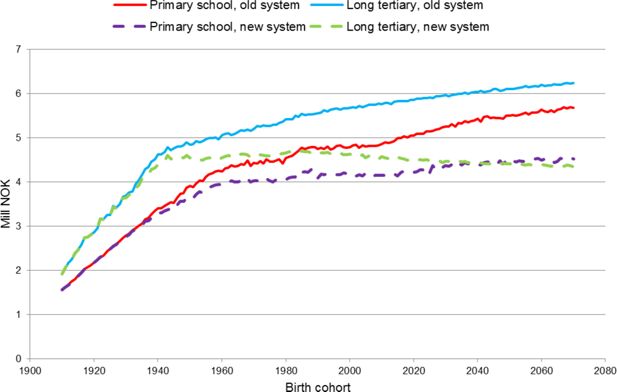
Gross discounted pension wealth at age 62 by level of education and pension system, NIS, net discount rate of 2 per cent. Mill NOK in 2011 amounts.
Growth in average gross pension wealth from the first cohorts included in the presentation is mainly caused by maturing of the former pension system introduced in 1967 as well as longer duration of life. As mentioned before, in the former system it was necessary with 40 years of accumulation to obtain full old age pension. Due to still low labour market participation rates for Norwegian women up to the 1970s, maturing of the system had a significant effect for average gross pension wealth for cohorts born up to the beginning of the 1960s. Increasing life expectancy also causes average gross pension wealth to increase for almost every cohort, but the effect is reduced by discounting and the fact that a greater part of the increasing life expectancy for later cohorts occurs at higher ages.
With the new pension system most of the effects from longer duration of life disappear because of the effects from the divisors on postponed retirement or on average pensions in the case if retirement age is unaffected. Therefore further growth in average pension wealth stagnates for the first cohorts affected by the new system, i.e. cohorts born in 1943 or later. Indexing of pension benefits in payment for already existing old-age pensioners from 2011 by wage growth minus 0.75 per cent even hurts gross pension wealth for cohorts born before 1943.
Persons with a high level of education have a higher average pension wealth because they have higher incomes caused by both higher earnings and higher participation rates, and because they live longer. Introduction of the former pension system in 1967 also had a more immediate effect for this group compared with the group with only primary school because a transition rule rewarded those cohorts born between 1920 and 1940 with high and stable participation in the labour market. The pension reform from 2011 causes a slightly falling level of average discounted gross pension wealth for younger cohorts with long tertiary education. Longer life expectancy, than for persons with low education, is the main reason why the graph has a more negative slope. Although persons with long tertiary education normally retire later than persons with primary school, longer life expectancy normally also means that they have more years as retired. Therefore their discounted pension wealth by the age of 62 is more hurt by indexing pension in payments less than wage growth than what is the case for persons with primary school. More years up to retirement for persons with long tertiary education compared to persons with primary school as their highest completed education also means a larger reduction of the present value of future pension benefits at age 62 for the latter group. Also note that a strong growth in the level of education from the cohorts born in the first part of the former century up to the cohorts born in the 1980s means that the graph for long tertiary education is far more representative for the whole population for the later cohorts compared to the older cohorts where the graph for primary school is the most representative.
If disability pensions and survivors’ pensions are added, as presented in Figure 5, the difference between different levels of education gets smaller. This is caused by a much higher share of disabled among those with only primary school compared to those with long tertiary education. Disability pensions also get a large weight because of the discounting since they normally occur about 20 years before old age pensions.
5.2 Net pension wealth
Net discounted value of pension wealth is obtained by subtracting estimated discounted value of contributions from the estimated discounted value of pension benefits, and this is shown for all inhabitants in different cohorts in Figure 6. There is a minor weakness in the calculations (and the figure) that it has not been possible to collect data for contributions to the old-age pension system up to 1960 for cohorts mainly born before 1940. Beyond that, the graph shows the expected course. The cohorts who established the pay-as-you-go system experienced a substantial gain by letting future generations pay.
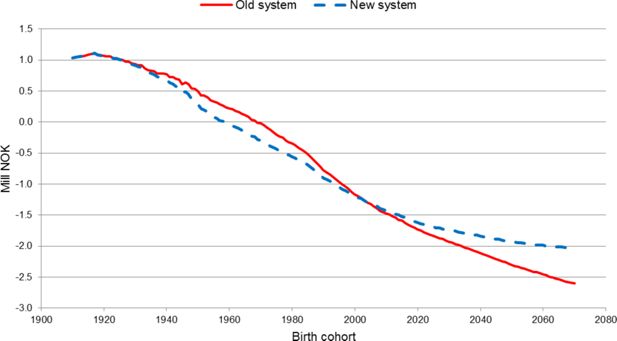
Net discounted value at age 62 for old age pension benefits and contributions, all inhabitants, net discount rate of 2 per cent. Mill NOK in 2011 amounts.
For later cohorts discounted value of benefits received is lower than discounted value of contributions mainly because each person contributes to the system first and receives old-age pensions afterwards. These results are to some degree congruent with the results for the Netherlands by Nelissen (1995), showing a smaller positive effect of the old-age pension system for the younger cohorts compared to the older. One reason for the difference compared to Norway is that the old-age pension system in the Netherlands was established in 1957, earlier than the Norwegian system.
In the overall analyses of distributional effects between generations from all governmental revenues and expenditures in Sweden by Pettersson et al. (2006), differences in net benefits between different cohorts naturally are much lower compared to what is the case when focus is limited to old age pension system. But also in Sweden persons born in the 1930s seem to have a more positive net gain from governmental revenues and expenditures than younger generations. Pettersson et al. also point at the fact that larger generations commonly are worse off than smaller regarding net benefits received from the government over the life cycle.
Measured by net discounted value, the cohorts who decided the Norwegian pension reform in 2011, i.e. cohorts born between 1930 and 2000 lose from the reform mainly because the reform reduces their future benefits. Younger cohorts gain from the reform mainly because discounted value of future contributions is reduced more than discounted value of future benefits.
Net discounted values for old-age pension benefits and contributions by gender are presented in Figure 7. Women get a higher return from the old-age part of NIS than men because they live longer and benefit more and are less hurt by the redistributive elements like minimum pensions, ceiling on accumulation of entitlements and accumulation of pension rights for unpaid care. This result is largely congruent with the results reported for Norway by Christensen et al. (2012) and with the findings for the Netherlands by Nelissen (1995). Because of smaller redistributive elements in the Dutch pension system, the difference between men and women regarding net benefits from the old-age-pension system is lower than in Norway. If we had included disability pension, redistribution from men to women in the Norwegian pension system would have shown up to be even stronger because a greater share of women than men receives this pension. However, men are somewhat better off than women as a result of the pension reform mainly because the ceiling for full accumulation of pension entitlements is somewhat increased. This is especially the case in the long run for the younger cohorts. But also the new system means a considerable redistribution of incomes from men to women over the life course.
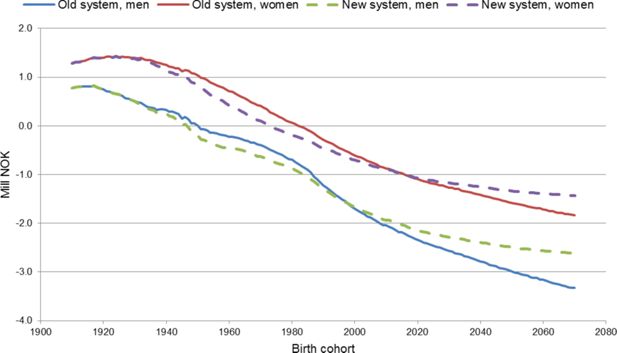
Net discounted value at age 62 for old age pension benefits and contributions by gender, net discount rate of 2 per cent. Mill NOK in 2011 amounts.
From Figure 8 it is evident that the old age pension system over the life cycle causes a significant redistribution from high educated to low educated, corresponding to a significant redistribution from persons with high incomes to persons with low incomes. By cohort this effect is strengthened during the maturing of the old system and is mainly caused by redistributive elements like minimum pension, ceiling on yearly incomes for accumulation of entitlements and entitlements for unpaid home care. Although Nelissen (1995) reports that the Dutch old age pension system over the life cycle redistributes incomes from high educated to low educated, the degree of redistribution seems to be much higher in Norway. Compared to most other countries, distributional elements in the Norwegian pension system are probably stronger. And because the old-age pension system is an integrated part of the government budgets there is no ceiling on financial contributions in the tax system, which is quite common in countries where the system is autonomous. Inclusion of disability pensions in the figure would have strengthened the picture of redistribution.
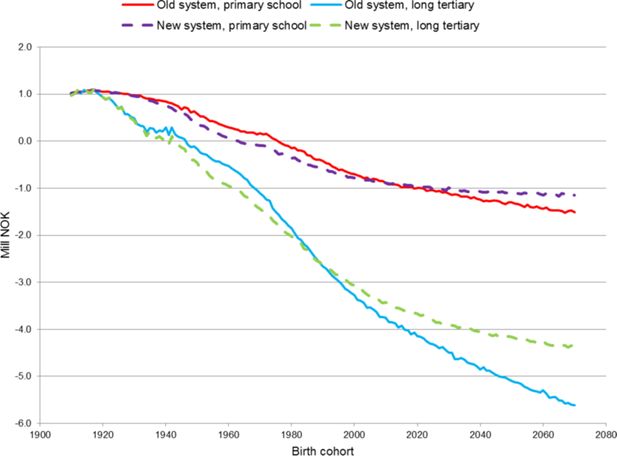
Net discounted value at age 62 for old age pension benefits and contributions by level of education, net discount rate of 2 per cent. Mill NOK in 2011 amounts.
A smaller distance between high and low educated (and thereby between high and low incomes) regarding net discounted value for old-age pension benefits and contributions when the new pension system has matured for the younger cohorts, indicates a somewhat smaller redistribution over the life cycle between high and low incomes in the reformed pension system compared to the old. Higher accumulation of entitlements for incomes somewhat above average with the new system as discussed in connection with Figure 1 is probably the main reason. But even with the new system there is still a significant redistribution over the life cycle between high and low educated.
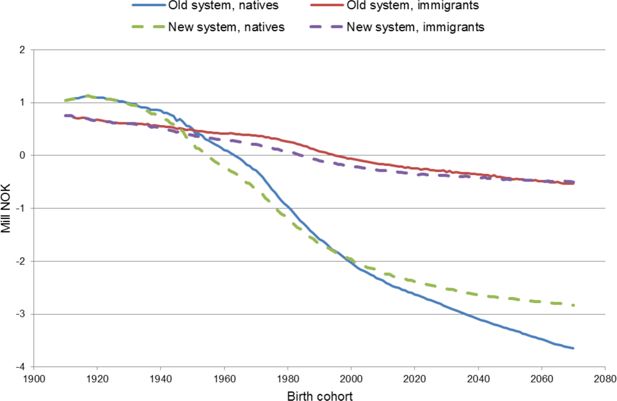
If the population is divided into natives and immigrants as shown in Figure 9, we see that net discounted value for old-age pension benefits is much more positive for immigrants than for natives. An average immigrant contributes less than an average native because of fewer years of work and lower labour incomes. As an old age pensioner many immigrants only will receive minimum pensions, eventually adjusted for a lower period of residence than necessary to achieve a full minimum pension. By same reasons several cohorts of average immigrants lose from the pension reform measured by net discounted value of old age pension because minimum pension also is assumed to be somewhat affected by life expectancy adjustments. However, for the cohorts born in the 1960s, who are the ones that lose most from the reform, the loss for an average native is significantly larger than the loss for an average immigrant. For younger cohorts born after 2000 natives benefit more from the reform than immigrants because of smaller contributions to the system.
5.3 Implicit net gain from the pension reform: sensitivity for main assumptions
The net discounted value of contributions to and benefits from old-age pensions for each cohort relative to the cohort’s total discounted labour incomes over the life course may be interpreted as an average net tax rate the cohort pay to finance the system. By comparing these cohort-specific net tax rates for old-age pensions with the old and the new system, we obtain information on the impact of the reform relative to each cohort’s discounted labour income. The effect on the net gain of the reform in per cent of labour incomes for an average native in each cohort is presented in Figure 10.
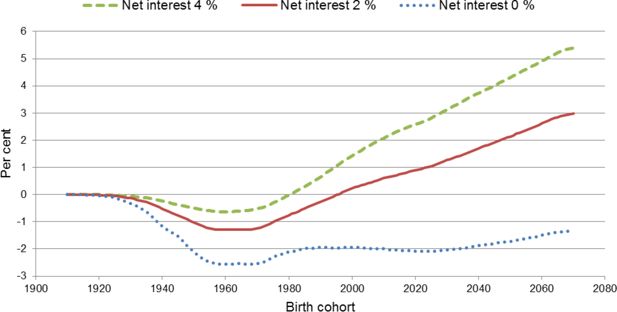
Change in net value for old age pensions for natives as a result of the pension reform. Change in per cent relative to labour incomes over the life course.
As discussed in Section, 4.4 results from calculations of discounted values are heavily dependent on the choice of net rate of interest, and effects from alternative assumptions are presented in Figure 10. With the standard assumption of a net rate of interest of 2 per cent that is quite common in the economic literature, cohorts born between 1950 and 1980 are those who are most hurt by the reform. But even for these cohorts the implicit net loss is not larger than 1.3 percentage points compared to the cohort’s discounted average labour income over the life course. The estimated loss is, however, based on the assumption that the old system could have been preserved without any problems. Estimated growth in contribution rates with the old system shown in Figure 3 indicates that this assumption is far from obvious. Figure 10 also shows that cohorts born after 2000 will gain from the reform with a net rate of interest of 2 per cent because the value of contributions as young is more worth than the corresponding value of benefits received as old.
With a net rate of interest of 4 per cent, discounted gain of lower contributions increases compared to discounted loss of lower old-age benefits. Fewer cohorts lose from the reform, and the loss is smaller compared to the calculations based on a net rate of interest of 2 per cent. Cohorts born after 1980 gain from the reform, and the gain is larger compared to calculations based on a smaller rate of interest. On the other hand, based on an assumption of a zero net rate of interest, no cohort gains from the reform during the period showed in the figure. Only natives are included in the presented series, and by prolonging the calculations we have checked that this group will experience a positive net gain from the reform in a longer perspective even with a zero net rate of interest. Also with a zero net rate of interest cohorts born between 1950 and 1980 are those who lose most. In the real world a situation with net rate of interest equal to zero is not sustainable in the long run. In this case there will be no budget constraint for the government. A large deficit now could be transferred into infinity.
Sensitivity for effects on old-age pension expenditures and labour supply from other aspects of relevance for the Norwegian pension reform is discussed by Fredriksen, Holmøy, Strøm, and Stølen (2015). Because the main aim of the reform is to counteract future growth in old-age pension expenditures caused by further growth in longevity, the tightening effect is highly dependent on this component. But although tightening for the cohorts born between 1950 and 1980 will be stronger if longevity grows more than assumed in the main alternative, the gain compared with maintaining the old system will also be stronger for the cohorts born after 2000. Although uncertainty regarding the effects on retirement age, and thereby the effect on labour supply, from the reform is rather large, the analyses by Fredriksen et al. (2015) show that the effect on old-age pension expenditures is relatively small. The actuarial system means that those who retire early are punished with low yearly benefits, while those who postpone retirement are rewarded with high.
References
-
1
Generational Accounts: A Meaningful Alternative to Deficit AccountingTax Policy and the Economy 5:55–110.
-
2
Actuarial Fairness When Longevity Increases: An Evaluation of the Italian Pension System. The Geneva Papers638–674, Actuarial Fairness When Longevity Increases: An Evaluation of the Italian Pension System. The Geneva Papers, 38.
- 3
-
4
Pension Reform in Norway: Combining NDC and Distributional GoalsIn: R Holzmann, E Palmer, D Robalino, editors. NonfinancialDefined Contribution Pension Schemes in a Changing Pension World: Progress, Lessons, and Implementation. Washington, DC: World Bank. pp. 129–154.
-
5
The progressivity of social security, NBER Working Paper 7250Cambridge Massachusetts: National Bureau of Economic Research.
- 6
-
7
Are Contributions to Public Pension Programmes a Tax on Employment?Economic Policy 19:267–311.
-
8
The First Wave of NDC Reforms: The Experiences of Italy, Latvia, Poland and SwedenIn: R Holzmann, E Palmer, D Robalino, editors. Nonfinancial Defined Contribution Pension Schemes in a Changing Pension World: Progress, Lessons, and Implementation. Washington, DC: World Bank. pp. 31–84.
-
9
Social SecurityIn: AJ Auerbach, M Feldstein, editors. Handbook of Public Economics, Vol. 4. Elsevier Science B.V. pp. 2245–2324.
-
10
Projections of Population, Education, Labour Supply and Public Pension Benefits, Analyses with the Dynamic Microsimulation ModelMOSARTProjections of Population, Education, Labour Supply and Public Pension Benefits, Analyses with the Dynamic Microsimulation ModelMOSART, Social and Economic Studies 101, Statistics Norway.
-
11
Uforming av ny alderspensjon i folketrygden (Design of the old-age pension in the National Insurance System for Norway). Reports 22/2011Statistics Norway.
-
12
Fiscal effects of the Norwegian pension reform — A micro-macro assessment. Discussion Papers No 821Statistics Norway.
-
13
Educational behaviour in the dynamic micro-simulation model MOSART. Reports 15/2013Statistics Norway.
-
14
How effective is redistribution under the social security benefit formula?Journal of Public Economics 82:1–28.
-
15
What has been learned about labour supply in the past twenty years?American Economic Review 83:116–121.
- 16
-
17
Welfare Reforms in European Countries: A Microsimulation AnalysisEconomic Journal 117:1–44.
-
18
The distributional aspects of social security and social security reformRedistribution in the current U.S. Social security system, The distributional aspects of social security and social security reform, University of Chicago Press.
-
19
The Reform of Pension Systems: Winners and Losers Across Generations in the United Kingdom and GermanyEconomica 67:203–228.
-
20
Lifetime income redistribution by the old-age state pension in The NetherlandsJournal of Public Economics 58:429–451.
-
21
Annual versus lifetime income redistribution by social securityJournal of Public Economics 68:223–249.
-
22
Micro analytic Simulation Models to Support Social and Financial PolicyNew York: North Holland.
-
23
Generationsanayser — Omfordelning mellan generationer i en växande välfärdsstat (Generational Analyses — Redistribution between Generations in an expanding Welfare State)Generationsanayser — Omfordelning mellan generationer i en växande välfärdsstat (Generational Analyses — Redistribution between Generations in an expanding Welfare State), Rapport til ESS, Expertgruppen för Studier i Samhällsekonomi, 2006:6, The Ministry of Finance, Sweden.
-
24
Population projections2016–2100, Population projections, https://www.ssb.no/en/befolkning/statistikker/folkfram.
-
25
Equity versus Efficiency in Public Pension Schemes - Microsimulating the Trade-off. Discussion Papers No 515Statistics Norway.
-
26
The lifetime impact of the retirement income system, a quantitative analysisThe Retirement System in Canada: Problems and Alternative Policies for Reform. Report of The Task Force on Retirement Income Policy to the Government of Canada, Appendix 5, 5.25.41.
Article and author information
Author details
Publication history
- Version of Record published: August 31, 2017 (version 1)
Copyright
© 2017, Fredriksen & Stølen
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.