A new heuristic in mutual sequential mate search
Abstract
In this paper, we propose a new heuristic to be used as a mate search strategy in the human mate choice model of Todd and Miller (1999). This heuristic, which we call Take the Weighted Average with the Next Desiring Date, is a plausible search rule in terms of informational assumptions. Our simulations show that this new heuristic is in terms of mating likelihood almost as good as, and in terms of mating speed always better than, the most successful —yet also unrealistic— heuristic of Todd and Miller (1999), namely the Mate Value-5 rule, which assumes that individuals in the mating population completely know their own mate values before interacting with any date. The success of our heuristic stems from its extreme power to lead an average individual in the mating population to always underestimate his/her own mate value during the adolescence (learning) phase of the mating process. While our new heuristic is also found to be successfully egalitarian in pairing up individuals, it does not perform well in terms of marital stability.
1. Introduction
A seminal work by Todd and Miller (1999) studies human mate choice with the help of a boundedly rational model where individuals follow a simple heuristic (feedback rule) as their mate search strategies. This model involves two phases, the first of which is called the adolescence phase. Individuals who have homogeneous preferences over the individuals of the opposite sex randomly interact with a number of dates sequentially in this phase and inform each of their dates regarding whether he/she was found desirable. Using these feedbacks, individuals adjust their aspiration levels after every interaction according to some rule used by the whole population. In the second phase, called the mating phase, individuals randomly interact with potential mates and decide to whom to make a proposal. At each stage of this phase, every pair of individuals are removed from the mating pool as a married couple if they have simultaneously proposed to each other. The mating phase ends after a stage at which either the mating pool contains no individuals or no pair of individuals inside the mating pool can form a married couple.
The adjustment rules used in the adolescence phase are five simple heuristics, called Take the Next Best, Mate Value-5, Adjust Up/Down, Adjust Relative, and Adjust Relative/2. According to Take the Next Best, each individual has an initial aspiration level of zero and after each instance of dating sets his/her aspiration to the mate value of his/her date provided that this date is desirable; that is, the mate value of this date exceeds his/her previous aspiration level. Under Mate Value-5, each individual always sets his/her aspiration level to a constant value that is lower than his/her own mate value by the value of 5. The other three adjustment rules set the initial aspiration level of each individual to the average mate value. Of these rules, Adjust Up/Down requires that each individual adjusts at each instance of dating his/her aspiration upwards (downwards) by a constant parameter if he/she is found by his/her date desirable (non-desirable). The Adjust Relative Rule is a modification of Adjust Up/Down with mutual desirability taking the place of desirability. Under this rule, an individual raises (reduces) his/her aspiration level by a constant parameter, if he/she and his/her date find each other desirable (non-desirable). In other possible cases, individuals make no adjustments. Finally, the rule of Adjust Relative/2 is similar to Adjust Relative with the difference that for each individual the adjustment parameter at any instance of dating is equal to the half of the difference between his/her previous aspiration level and the mate value of his/her present date.
Computer simulations of Todd and Miller (1999) for the mate search model described above show that the mating likelihood, as measured by the number of mated pairs in the population, always attains the highest values under the rule of Mate Value-5, extremely differing from the other rules. In addition, with respect to a notion of mating stability that is measured by the mean within-pair difference in mate value, mated pairs formed always become more stable under Mate Value-5 than under Adjust Up/Down, Adjust Relative, and Adjust Relative/2. In fact, Mate Value-5 also performs better than Take the Next Best when the adolescence length is short to medium. Overall, Mate Value-5 becomes the best search rule both in pairing up a great proportion of the population and in pairing up individuals with almost identical mate values. But, unfortunately, this rule has a very serious problem. It is based on the unrealistic assumption that each individual enters the adolescence phase of mate search by already knowing his/her own mate value, while one should be aware of the fact that:
“Knowing one’s own mate value is not necessarily an easy thing. We cannot be born with it, because it is both context sensitive (it depends on the others around us) and changes over time as we develop. We cannot simply observe ourselves to determine it, because we do not see ourselves in the same way that the others who judge us as potential mates see us. We do not even know the proper criteria on which to judge ourselves from the perspective of the opposite sex. Without this initial knowledge, then, we must somehow estimate our own mate value, if we are to use it to form our aspiration level.”
In line with the above view, all search rules of Todd and Miller (1999), apart from the self-centered and unrealistic rule of Mate Value-5, have the goal of correctly estimating one’s own mate value to use it as a proxy for one’s own aspiration level. Of these rules, Adjust Relative/2 becomes superior to the other realistic rules of Todd and Miller (1999) with respect to a success measure that appropriately balances the likelihood and stability of matings. However, if the individual performances of Adjust Relative/2 and Mate Value-5 are compared, one can see, irrespective of the adolescence length, around a two-fold difference between the mating likelihoods generated by these two search rules always in favor of Mate Value-5. Clearly, Adjust Relative/2, which is plausible as a rule, is not a successful alternative to the unrealistic rule of Mate Value-5. This brings us to the following question: Can we find a heuristic that is plausible and that is almost as successful as Mate Value-5 in terms of likelihood of mating? The answer we provide in this paper is ‘yes’. We introduce a realistic heuristic, which we call Take the Weighted Average with the Next Desiring Date, yielding almost as high likelihood of mating as Mate Value-5, especially when the adolescence length is long.
Here, we should note that neither the focus of Todd and Miller (1999) nor ours is to propose an optimal search strategy. In fact, the computational complexity of the sequential human mate choice problem has not allowed, so far, the related literature to come up with a theoretical result showing the existence of an optimal search strategy.1 Like in Todd and Miller (1999), our aim is only to find a ‘satisficing’ rule, a heuristic that is simple in terms of knowledge, fast, egalitarian/balanced and stable. In line with this aim, we investigate whether our simple heuristic —that unlike the Mate Value-5 Rule of Todd and Miller (1999) indirectly takes the self mate values of individuals into consideration and always produces a very high likelihood of mating— also fares well with respect to some additional success measures concerning the balancedness, the stability, and the speed of mating.
Our work, which closely follows Todd and Miller (1999), can be located within a strand of literature which models human mate search with the help of some dating phase where individuals can approximate their own mate values by using feedbacks from potential mates they date (see, for example, Dombrovsky & Perrin, 1994; Mazalov, Perrin, & Dombrovsky, 1996; Todd, 1997; and Collins, McNamara, & Ramsey, 2006). Two recent related works in this literature are Shiba (2013) and Saglam (2014). Shiba (2013) extends the symmetric two-sided sequential mate search model of Todd and Miller (1999) to an asymmetric case (of firm or job with worker matching), and evaluates how the mating outcome changes when the two sides of the mating population use different adjustment rules (with one of the sides, the firms, using Mate Value-5 and the other side, the workers, using Adjust Relative/2). Findings of this study involve that the likelihood and stability of mating are similar under the symmetric and asymmetric cases, while the average value of successful individuals (workers) are higher under the asymmetric case, pointing to the failure of individuals with relatively low values in finding mates (jobs). Saglam (2014) studies a similar robustness problem regarding whether any search rule of Todd and Miller (1999) can be used as a Nash (1950) equilibrium strategy by the whole population so that no individual would have an incentive to unilaterally deviate from that search rule to any other rule so as to increase the likelihood of his/her mating. Simulations of Saglam (2014) show that in terms of this game-theoretical stability concept, Adjust Relative on average performs better than the other four search rules of Todd and Miller (1999).
The rest of our paper is organized as follows: In Section 2 we present the model which we borrow from Todd and Miller (1999). We present five heuristics (search rules) introduced by Todd and Miller (1999) for this model in Section 3, where we also run computer simulations to explore why some of these heuristics are more successful than the others. In Section 4 we introduce our new heuristic and in Section 5 we evaluate its performance by computer simulations. Finally, we conclude in Section 6.
2. Model
We borrow our model from the mutual sequential mate search model of Todd and Miller (1999). This model considers a set of individuals, N = {1, 2, . . . , 2n}, involving n males and n females each of whom searches for some mate from the opposite sex. Each individual has a mate value which is always unknown to himself/herself while completely observable to any individual interacted with in any phase of mate search. The mate value of individual i, denoted by v(i), is randomly drawn from the uniformly distributed values over some interval of reals [0, V] that is common for all individuals.
Mate search involves two phases: the adolescence phase and the mating phase. Individual i enters the adolescence phase with an initial aspiration level, denoted by a(i, 0), and then randomly and sequentially meets a fixed number of dates of the opposite sex. This fixed number is common for all individuals and denoted by the integer S satisfying 1 ≤ S ≤ n, implying that the adolescence phase consists of S stages of dating. At each stage s = 1, . . . , S, individual i observes the mate value of his/her date d(i, s) and after comparing this value with his/her aspiration level of the previous stage a(i, s – 1), individual i decides whether his/her date in stage s is desirable as a potential mate. Next, individual i and his/her date d(i, s) in stage s exchange information as to whether they find each other desirable.
Finally, taking this information into account, individual i determines his/her aspiration level, a(i, s), for stage s using some adjustment (feedback) rule commonly used by the whole population. (We will describe the adjustment rules introduced by Todd and Miller (1999) in the next section.) After the adolescence phase is over, individuals enter the mating phase, where males and females are randomly paired with potential mates they did not interact with in the adolescence phase. Here, individual i observes the mate value of his/her partner and compares it with his/her finalized aspiration level a(i, S) to decide whether to make a proposal. If the individuals in a random pair propose to each other, then they are mated and removed from the mating pool. Otherwise, both individuals become available for the next stage. The mating phase ends when the mating pool becomes empty or each of its member has already been paired with all potential mates inside the mating pool.
3. Aspiration-Adjustment Heuristics of Todd and Miller (1999)
Below, we describe five aspiration-adjustment heuristics (or simply mate search strategies or rules) introduced by Todd and Miller (1999).
Take the Next Best (TNB) Rule
Individual i sets the aspiration in stage s to the mate value of his/her current date if individual i finds this date desirable, and makes no adjustment otherwise.
Mate Value-5 (MV-5) Rule
This rule sets the aspiration at the beginning of the adolescence phase to the constant v(i) – 5, and does not change it. Thus, in any stage s,
The above rule assumes that each individual knows his/her mate value. Also note that the constant of 5 in the definition of the rule is chosen by Todd and Miller (1999) when the maximal mate value V is equal to 100. So, this rule can be generalized as Mate Value–0.05V Rule.
Adjust Up/Down (AUD) Rule
In stage t, individual i adjusts up the stage s − 1 aspiration by the constant
Adjust Relative (AR) Rule
Here, there is the possibility of non-adjustment, as well. Individual i adjusts up the stage s – 1 aspiration by the constant
Adjust Relative/2 (AR/2) Rule
This is a modification of the Adjust Relative Rule in that the size of adjustment in stage s is equal to the half of the difference between the stage s – 1 aspiration level of individual i and the mate value of his/her date in stage s; i.e., β (i, s) = |v(d(i, s)) – a(i, s – 1)|/2.
The initial aspiration level of individual i is assumed to be a(i, 0) = 0 under Take the Next Best, a(i, 0) = v(i) – 5 under Mate Value-5, and a(i, 0) = V/2 under the other three rules.
To evaluate the performances of the mate search strategies described above, Todd and Miller (1999) conducted a set of computer simulations. For their simulations they set n to 100 to consider a population involving 100 males and 100 females. For this population, they randomly assigned all mate values from the discrete uniformly distributed values over the integers in [0, V] where V was set to 100. Under these settings, they conducted 100 Monte Carlo simulations for each integer adolescence length S between 1 and 90.
One of the success measures they used was the likelihood of mating, as represented by the number of mated pairs formed in 100 potential pairs. Their simulations according to this measure, which we have reproduced and illustrated in Figure 1, show that Mate Value-5 dominates the other four rules, yielding an incomparably high likelihood of mating especially for small to medium values of adolescence length.3 Under the other four search rules, the likelihood of mating is found to be around 50% for very low levels of adolescence length, while it quickly drops to almost zero under the rule of Take the Next Best as the adolescence length starts to increase. In fact, Take the Next Best is dominated by every other rule on average. Of the remaining rules, Adjust Relative/2 performs mildly better than both Adjust Relative and Adjust Up/Down for short to medium adolescence lengths, whereas the converse becomes true when the adolescence length is long.
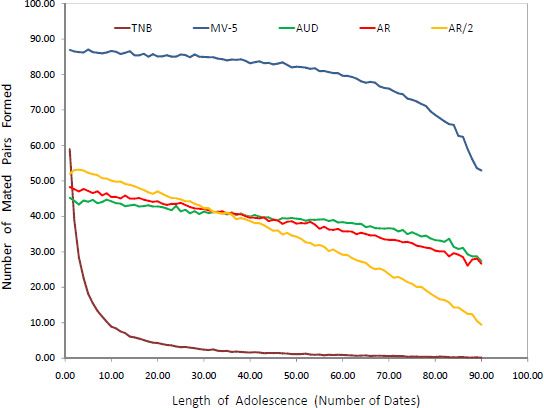
Number of mated pairs formed under the search rules of Todd and Miller (1999).
A second success measure, introduced by Todd and Miller (1999), for assessing mate search strategies is concerned with the mean mate value of all mated individuals. According to this measure, a search strategy is considered successful at a given adolescence length if the mean mate value of all mated individuals is sufficiently close to the middle mate value in the population, enabling a great portion of the population to find mates. Figure 2 shows that with respect to this second success measure the worst strategy is Take the Next Best, under which the mean mate value very quickly rises towards the maximal mate value in the population. This is because that under this rule aspirations become so high that individuals with low or medium mate values are not likely to end up in a mutually agreeable (desirable) mating. Evidently, the most ‘balanced’ search strategy is Mate Value-5, which generates a mean mate value around 50 for all adolescence lengths. This result is not surprising given the power of Mate Value-5 in pairing up individuals. Figure 2 also shows that individuals who find mates are essentially the top half of the population under Adjust Relative and the bottom half of the population under Adjust Up/Down. Whenever Mate Value-5 is left aside, the most successfully egalitarian (balanced) search strategy becomes Adjust Relative/2, especially when the adolescence length is medium to long.

Mean mate value of all mated individuals under the search rules of Todd and Miller (1999).
A third success measure introduced by Todd and Miller (1999) considers the stability of mating, as defined by the mean within-pair difference in mate value. Rules that have lower scores with respect to this measure are considered to perform better as they would lead to more stable matings. The performances of the mate search strategies of Todd and Miller (1999) with respect to this measure, according to our simulations, are illustrated in Figure 3. Once again, Mate Value-5 is found to be the best rule for short to medium adolescence lengths, yielding an extremely low mean within-pair difference in mate value. As a matter of fact, this rule yields more stable matings than the other rules with the exception of Take the Next Best. Although Take the Next Best is the worst rule with respect to the stability measure for very low adolescence lengths, it becomes at least as good as Mate Value-5 and always dominates the other three rules when the adolescence length is not very short. Over the same range of adolescence lengths, it is also found that Adjust Relative/2 is always superior to Adjust Up/Down, the latter of which on the other hand is always superior to Adjust Relative.

Mean within-pair difference in mate values under the search rules of Todd and Miller (1999).
An important success measure —which is not considered by Todd and Miller (1999) to evaluate two-sided mate search strategies— is the average time (measured by the number of interactions in the mating phase) to find a mutually agreeable/desirable mate. With respect to this measure a particular strategy is more successful if the number of potential mates checked by an individual during the mating phase is lower. We illustrate the performances of the search strategies of Todd and Miller (1999) according to this fourth success measure in Figure 4. One can observe that the time to find a mutually agreeable mate is increasing in the adolescence length for all five search strategies. As expected, the worst overall performance belongs to Take the Next Best, under which the aspirations of individuals become outstandingly high, resulting in very long periods of interactions in the mating phase before some successful pairs are formed. Interestingly, Adjust Relative/2, which fares quite well with respect to the other three success measures, has the second worst performance in terms of the time to mate. As a matter of fact, its performance is only slightly superior to that of Take the Next Best.
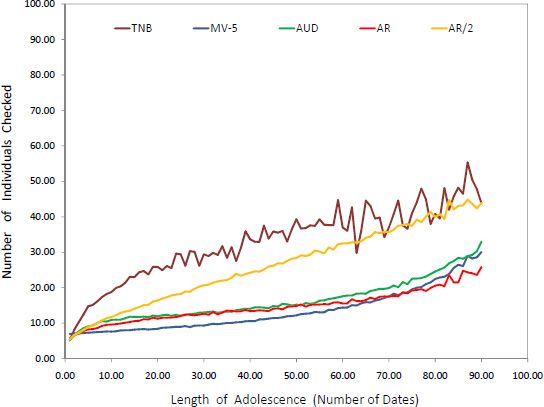
Number of individuals checked under the search rules of Todd and Miller (1999).
Figure 4 also shows that in general the highest speed of mating is obtained under Mate Value-5. Since the aspiration of an individual with the mate value x is always x−5 under this rule (when the maximal mate value is 100 points), each individual in the mating phase has a positive likelihood of finding a mutually agreeable mate within a group of potential mates with mate values ranging from max{0, x−5} to min{x+5, 100}. In other words, each individual —unless he/she is in the top or bottom 5 percent of the population— is mutually agreeable to exactly 10 percent of the potential mates, definitely a very large set.4 Because of this high rate of mutual eligibility for a great fraction of the mating population, individuals can find their mates under the Mate Value-5 Rule not only with a very high likelihood but also in a very short time.
We should note here that adding the fourth success measure, the speed of mating, into the picture changes the main conclusion of Todd and Miller (1999). By evaluating their mate search rules only with respect to the first three of the four success measures considered above, and resultingly by taking only Figures 1, 2, and 3 into account, Todd and Miller (1999) concluded that Adjust Relative/2 is (the second best rule or) the best rule if one leaves Mate Value-5 aside. However, Figure 4 reveals that Adjust Relative/2 is dramatically inferior to two other rules, namely Adjust Up/Down and Adjust Relative in terms of mating speed. When all four success measures are taken into consideration, none of the three rules, namely Adjust Up/Down, Adjust Relative, and Adjust Relative/2, can be argued to be significantly superior to any of the remaining two rules. As a matter of fact, considering Figures 1, 2, 3, and 4 together, we see that the comparisons of the mate search strategies, except for Mate Value-5, depend on the adolescence length. To obtain a brief account of these comparisons, we calculate in the below table the mean and standard deviation values for each of the four success measures (reported in Figures 1, 2, 3, and 4) over the set of adolescence lengths {1, 2, . . ., 90}.
The mean and standard deviation values for the success of search rules by Todd and Miller (1999).
Success Measure |
TNB |
MV-5 |
AUD |
AR |
AR/2 |
|---|---|---|---|---|---|
| Number of Mated Pairs Formed | 4.172 (8.456) |
79.683 (4.110) |
39.018 (5.835) |
38.523 (12.327) |
34.751 (12.327) |
| Mean Mate Value of All Mated Individuals | 95.773 (5.940) |
50.029 (0.303) |
29.469 (7.762) |
76.196 (3.080) |
56.664 (4.129) |
| Mean Within-Pair Difference in Mate Valu | 3.186 (3.626) |
2.706 (0.029) |
5.215 (1.257) |
8.904 (0.741) |
4.171 (2.345) |
| Number of Individuals Checked | 32.841 (10.141) |
13.490 (6.032) |
16.317 (5.810) |
14.674 (4.372) |
26.336 (10.787) |
Taking Figures 1, 2, 3, and 4 and Table 1 together, we observe that Take the Next Best has the worst overall performance, while Adjust Up/Down, Adjust Relative, and Adjust Relative/2 have comparable performances, with none of them clearly dominating any of the other two rules with respect to more than two success measures. However, it is very clear that Mate Value-5 is the best search rule in pairing up a great proportion of the population, in being balanced/egalitarian, in pairing up individuals with almost identical mate values, and in pairing up individuals in the shortest time. But, unfortunately, this rule is based on the unrealistic assumption that each individual enters the ado-lescence phase of mate search by already knowing his/her own mate value. As a matter of fact, this unrealistic rule is a member of a class of humble search rules called Mate Value-α where individuals constantly underestimate their own mate values by the value α ≥ 0. Given the class of search rules Mate Value-α, one may ask why we should restrict ourselves to the particular value of α = 5. Unfortunately, the answer to this question is not available in Todd and Miller (1999). To provide an answer, we have simulated the human mate choice model under the rule of Mate Value-α for two symmetric values around the constant 5 and obtained the results in the below table.
The mean and standard deviation values for the success of Mate Values for the success of Mate Value-α.
Success Measure |
α = 2 |
α = 5 |
α = 8 |
|---|---|---|---|
| Number of Mated Pairs Formed | 78.018 (0.418) |
79.683 (8.045) |
89.734 (0.483) |
| Mean Mate Value of All Mated Individuals | 49.966 (0.418) |
50.029 (0.303) |
50.023 (0.376) |
| Mean Within-Pair Difference in Mate Valu | 1.201 (0.013) |
2.706 (0.029) |
4.172 (0.029) |
| Number of Individuals Checked | 12.509 (0.159) |
13.490 (0.159) |
5.008 (0.058) |
Recall that Todd and Miller (1999) considered only the first three of the four success measures in Table 2. So, if one leaves the fourth success measure —namely the speed of mating— out of consideration like they did, the choice of α = 2 can be rationalized with respect to the third success measure (mating stability) and the choice of α = 8 can be rationalized with respect to the first success measure (mating likelihood), whereas the choice of α = 5 can be rationalized with respect to an aggregate success measure that appropriately balances the mating likelihood and the mating stability. On the other hand, when the fourth success measure is also taken into account, the choice of α = 8, which yields a superior performance with respect to both mating likelihood and mating speed, can be considered as a solid alternative to the choice of α = 5. So, in Section 5, where we will compare the performance of our new mate search strategy (to be described in Section 4) to that of Mate Value-5, we will also address how our strategy would fare in comparison to Mate Value-8.
We should also note that a limiting member of the class Mate Value-α, namely Mate Value-0, is the search rule under which no estimation errors are ever made. In the mutual sequential search model of Todd and Miller (1999), if the mate values of all males and females are drawn from the same discrete distribution and no individual, male or female, would desire to be paired up with another individual who has a lower mate value than his/her aspiration level, then a search rule, like Mate Value-0, under which all individuals always know/learn their own mate values must yield a likelihood of mating as high as 100 percent and a mean within-pair difference in mate value as low as zero.5 Given the findings in Figure 1, we can infer that under no realistic search rule of Todd and Miller (1999) can individuals estimate their mate values with a high precision. We can further claim that under some of search rules of Todd and Miller (1999), especially under Take the Next Best, the estimation errors of individuals must be extremely high if a positive link exists between the likelihood of mating and the precision of information individuals in the mating population obtain about their own mate values during the adolescence phase. Below, we will explore the existence of such a link.
Formally, we define the precision of information obtained by individuals in the mating population during the adolescence phase as the inverse of the root mean square error (RMSE) they make in estimating their own mate values at the end of S stages of dating, i.e.,
In Figure 5, we plot RMSE generated by each search rule of Todd and Miller (1999). Interestingly, there is a striking similarity between Figure 3 and Figure 5. If the rule of Take the Next Best is excluded, it is even possible to make —using these two figures— the generalization that a search rule is more stable than another search rule if it yields a lower RMSE. The exception with Take the Next Best is due to the fact that under this rule the aspiration of each individual quickly converges towards the highest mate value in the population. Hence, under this rule most individuals extremely overestimate themselves in the adolescence phase. This implies that in the mating phase only a tiny fraction of the population becomes able to find mates, while this tiny fraction involves only some elite members of the mating population who make almost no estimation errors. This is because these elite members have extremely high mate values and interacting with a desirable date is therefore very unlikely for them. Consequently, the mean within pair-difference in mate value becomes very low under the Take the Next Best Rule.

Root Mean Squared Error (RMSE) generated by the search rules of Todd and Miller (1999).
Another observation from Figure 5 is that RMSE becomes very low under Mate Value-5, attaining a constant value of 5 by the definition of the rule. One can argue that this finding is consistent with a claim stating that the lower the RMSE of individuals in estimating their own mate values, the more successful a search rule in terms of the mating likelihood. But, one should not rush to conclude this, as this claim can be easily rejected once one also considers the rule of Adjust Relative/2. Even though the RMSE values calculated for Adjust Relative/2 and Mate Value-5 are almost the same for medium to long adolescence lengths, there is a huge and puzzling difference between the mating likelihoods of these two rules over the same range of adolescence lengths, as one can recall from Figure 1.
To shed light on this puzzle, we report in Figure 6 our calculations for the mean aspiration level of all individuals at the end of the adolescence phase. Apparently, the mean aspiration levels under the search rules of Adjust Up/Down, Adjust Relative, and Adjust Relative/2 are always around the value of 50, which is also the mean level of mate values of all individuals. This should not be surprising though, since under each of these three rules, where the initial aspiration level is 50, not only are the upward and downward adjustments always of the same magnitude but also the conditions as to when to make these adjustments are symmetric.

Mean aspiration level of all individuals under the search rules of Todd and Miller (1999).
Comparing the performances of Mate Value-5 and Adjust Relative/2 in Figures 5 and 6 reveals that the precision of information acquired in the adolescence phase of mating process, or the magnitude of estimation errors made by individuals, is not a sufficient indicator of the success of a mate search rule. Evidently, the direction in which individuals make estimation errors also matters. As a matter of fact, individuals always underestimate their own mate values under the search rule of Mate Value-5, while the likelihoods of underestimating and overestimating can be inferred, from Figure 6, to be the same under Adjust Relative/2. So, it seems that the success of Mate Value-5 stems from the humbleness of individuals in setting their aspirations under this rule always sufficiently below their own mate values
Overall, we can say that of the five search rules proposed by Todd and Miller (1999) the most successful one, Mate Value-5, is not realistic while the other rules do not lead to a level of learning —in the adolescence phase— that can ensure a high likelihood of mating. This brings us to the following question: Can we find a simple search rule which is not self-centered (and unrealistic) like Mate Value-5 and under which the mating outcome is almost as likely as under Mate Value-5? We will explore this question in the rest of our paper.
4. A New Aspiration-Adjustment Heuristic
Given our observations in the previous section as to the reasons underlying the relative success of Mate Value-5, we will consider a search rule that can be predicted to yield humble aspirations. The initial aspiration level of each individual under this rule is set to zero, and if an individual finds out that her date is desiring him/her in any stage s of the adolescence phase, then he/she will set the stage-s aspiration level to the weighted average of his/her aspiration in stage s − 1 and the mate value of his/her date in stage s. Here, the relative weight of the stage s − 1 aspiration becomes equal to the number of incidents that the condition for updating was satisfied until the end of stage s − 1. Because of this, our weighted average rule actually sets the aspiration level of any individual at any particular stage of dating precisely to the arithmetic average of the mate values of all of his/her past dates satisfying the condition for updating. More formally, this search rule is described as follows:
Take the Weighted Average with the Next Desiring Date (TWAND) Rule: If individual i finds that his/her date in stage s is desiring him/her, then individual i sets the stage-s aspiration to the weighted average of his/her stage s − 1 aspiration and the mate value of his/her current date, using the respective weights of m/(m + 1) and 1/(m + 1) with m denoting the number of the previous stages (before stage s) in which individual i was found desirable by his/her date. Otherwise, individual i makes no adjustment.
The above rule brings two modifications over the Take the Next Best Rule of Todd and Miller (1999). One modification replaces the action of ‘taking the next satisfactory date’ with ‘taking the weighted average with the next satisfactory date’, while the other modification changes the condition as to when a date is found to be satisfactory. Whereas under Take the Next Best an individual finds a date satisactory if he/she desires this date, under TWAND an individual finds a date satisfactory if this date is desiring him/her.
Also note that under the rule of TWAND any individual with a positive mate value will certainly be found desirable by his/her first date since the aspirations of all individuals are initially zero. Then, after the first stage of dating the aspiration level of each individual will be positive with probability one. In fact, just because of this, starting with the second dating stage, each individual will face the likelihood of being found non-desirable by some of his/her dates. Since this likelihood is higher for individuals with lower mate values, these individuals will have lower levels of aspirations on average, due to the definition of the search rule. On the other hand, the lower the mate value of the date of an individual, the higher the likelihood that this individual will be found desirable. As a consequence, interacting with a date will reduce —after some dating stage— the aspiration of each individual on average. One can then predict for the whole population that starting from some dating stage, the mean level of aspirations will always be below the mean level of mate values and they will decrease as the number of dating interactions becomes higher. One can also predict that the anticipated decrease in aspirations under our new mate search rule, TWAND, will possibly lead to an increase in the mating likelihood and to a decrease in the average time (or the number of interactions) to find a mutually agreeable mate. We will be able to directly check these predictions in the next section.
At this point, one may ask why we should not consider a more humble (and much simpler) mate search strategy than TWAND if we believe that the success of Mate Value-5 stems from its humbleness in setting aspirations. In fact, a natural candidate for this is the strategy described below.
Zero Aspiration (ASP = 0) Rule: This rule sets the aspiration at the beginning of the adolescence phase to zero (i.e., the lowest possible mate value), and does not change it. Thus, in any stage s,
We should note here that the above rule is not informationally unrealistic like Mate Value-5. As a matter of fact, it simply requires no information about anything. But, on the other hand, it is extremely restrictive and ‘behaviorally unrealistic’ since under this rule individuals are assumed to be so humble that each of them always perceives himself/herself as the least desirable mate in the population. Because of this, each individual under this rule would be ready to propose to any individual that he/she will interact with in the mating phase as well as to accept any proposal that he/she may receive. This implies that every individual in the population would always be paired with a mutually agreeable mate and, moreover, this pairing would occur during the first interactions in the mating phase. Definitely, these nice outcomes may be sufficient for us to consider the ASP = 0 rule as a benchmark. However, one may also predict that since under this rule everybody would always find everybody mutually agreeable as a mate, the resulting matings would be potentially very unstable, pairing up individuals with very diverse mate values. We will be able to check this last prediction in the next section, where we will calculate and study the performances of our new rule TWAND and the benchmark rule ASP = 0, in comparison to the performances of the mate search rules of Todd and Miller (1999).
5. Simulations
We measure the performance of our new search rule using computer simulations. We conduct these simulations using the settings considered by Todd and Miller (1999). Therefore, we set n to 100 and randomly assign all mate values from the discrete uniformly distributed values over the integers in [0, V where V was set to 100. Given these settings, we conduct 100 Monte Carlo simulations for each integer adolescence length S between 1 and 90. We perform these simulations with the help of Gauss Version 3.2.34 (Aptech Systems, 1998). The source code of the simulation program and the resulting data are available from the author upon request.
In Figure 7, we plot the mean aspiration level of all individuals for all search rules we consider in this study. This level is always zero for the rule of ASP = 0, by definition. We also observe that the mean aspiration level is lower for TWAND than for any search rule of Todd and Miller (1999) irrespective of the adolescence length. This means that TWAND is always more humble than even the most humble search rule of Todd and Miller (1999), namely Mate Value-5.
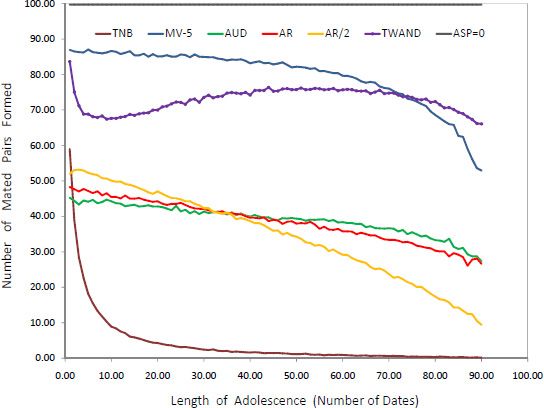
The next four figures will show the performances of TWAND, ASP = 0, and the five search rules of Todd and Miller (1999) with respect to four success measures considered in Section 3. Figure 8 illustrates the mating likelihoods generated by the studied search rules. As expected, every individual is always paired under ASP = 0. We also observe that TWAND is always outstandingly superior, in terms of mating likelihood, to all search rules of Todd and Miller (1999), except for Mate Value-5. Besides, when the adolescence length is sufficiently long, TWAND is superior to Mate Value-5, as well.
Now, we consider the performances of all search rules with respect to the mean mate value of the mated pairs. Figure 9 shows that ASP = 0 is perfectly egalitarian, as a result of the ability of this rule in pairing up all individuals in the mating population. We also observe that Mate Value-5 and ASP = 0 are always superior to TWAND, whereas Adjust Relative/2 is superior to TWAND provided that the adolescence length is not very small. On the other hand, TWAND is superior to Take the Next Best and Adjust Relative at all adolescence lengths, and also to Adjust Up/Down if the adolescence length is not very small.
Next, we consider the stability measure. The results of our simulations in Figure 10 shows that TWAND leads to more unstable pairs (or a higher mean within-pair difference in mate value) than any search rule of Todd and Miller (1999) irrespective of the adolescence length. We claim that the observed poor stability performance of our search rule is possibly caused by its humbleness in setting aspirations. In fact, this claim seems to be supported by the outstandingly poor stability performance of ASP = 0, the most humble search rule one can consider in the model of Todd and Miller (1999).
Finally, in Figure 11 we consider for all search rules the average time (or effort) to pair, as measured by the number of individuals seen in the mating phase. Under ASP = 0, each individual pairs up with the first individual interacted in the mating phase, as predicted. We also observe that TWAND, which requires —at almost all adolescence lengths— at most 10 individuals to be checked on average, is superior to all search rules of Todd and Miller (1999) in terms of time to pair. It seems that the humbleness of TWAND in setting aspirations is not only responsible for the poor performance of this rule with respect to the mating stability (Figure 10) but also its superior performance with respect to the mating speed (Figure 11).
In Table 3, which extends Table 1, we report the mean and standard deviation values for success corresponding to all search rules studied in this paper, including TWAND, ASP = 0, and the five search rules of Todd and Miller (1999). Taking Figures 8, 9, 10, 11 and Table 3 into consideration, we observe that both mating and divorcing are more likely under the rule TWAND than under any realistic search rule of Todd and Miller (1999), including Take the Next Best, Adjust Up/Down, Adjust Relative, and Adjust Relative/2. Besides, the mating outcome is more balanced/egalitarian under TWAND than under any realistic search rule of Todd and Miller (1999), except for Adjust Relative/2. Moreover, TWAND is faster in pairing up individuals in the mating phase than all of the search rules of Todd and Miller (1999), including the unrealistic rule of Mate Value-5 as well.
The mean and standard deviation values for success corresponding to all studied search rules.
| Success Measure | TNB | MV-5 | AUD | AR | AR/2 | TWAND | ASP = 0 |
|---|---|---|---|---|---|---|---|
| Number of Mated Pairs Formed | 4.172 (8.456) |
79.683 (8.045) |
39.018 (4.110) |
38.523 (5.835) |
34.751 (12.327) |
72.785 (3.205) |
100.000 (0.000) |
| Mean Mate Value of All Mated Individuals | 95.773 (5.940) |
50.029 (0.303) |
29.469 (7.762) |
76.196 (3.080) |
56.664 (4.129) |
60.040 (1.343) |
49.995 (0.207) |
| Mean Within-Pair Difference in Mate Value | 3.186 (3.626) |
2.706 (0.029) |
5.215 (0.029) |
8.904 (0.741) |
4.171 (2.345) |
14.222 (2.593) |
33.384 (0.245) |
| Number of Individuals Checked | 32.841 (10.141) |
13.490 (6.032) |
16.317 (5.810) |
14.674 (4.372) |
26.336 (10.787) |
7.931 (3.316) |
1.000 (0.000) |
Re-inspecting Table 2 in Section 3, which reports the overall performances of Mate Value-2 and Mate Value-8 in addition to that of Mate Value-5, we can see that TWAND, which is in general slightly inferior to Mate Value-5 and also inferior to Mate Value-8, is more comparable to Mate Value-2. This result is not surprising since given a rule of the form Mate Value-α, a decrease in the parameter α actually reduces the average humbleness of this rule, which in turn renders TWAND, the average humbleness of which is always constant, a relatively stronger alternative.
In Figure 12 we report for each studied search rule the RMSE of estimating mate value for all individuals. Apparently, the RMSE values are much higher for TWAND than for Mate Value-5, under the latter of which the errors of estimations are always 5 points, by definition. In fact, with respect to the RMSE values, TWAND is found to be superior to only two rules that generate extremely high or low aspirations: the rule of ASP = 0 under which aspirations are always zero and the rule of Take the Next Best under which aspirations quickly rise up towards the highest mate value in the population.
Considering Figures 8, 9, 10, 11, and Figure 12 together, it seems that the observed similarity in the performances of TWAND and Mate Value-5 with respect to mating likelihood, mating balancedness, and mating speed is unrelated to the respective powers of these two rules in estimating mate values of individuals. Indeed, as implied by Figure 7, the similarity in performances of these two rules seems to be the result of their humbleness in setting aspirations.
6. Conclusions
In this paper, we have attempted to first uncover why some of the simple heuristics or search strategies in the human mate choice model of Todd and Miller (1999) are more successful than the others, and benefiting from our answer to this question we have proposed a new heuristic that is in terms of mating likelihood as good as, and in terms of mating speed much better than, the most successful, yet also unrealistic, heuristic of Todd and Miller (1999), namely Mate Value-5. Regarding our first object, we have calculated, for each heuristic of Todd and Miller (1999), the Root Mean Square Error made by all individuals in the mating population in estimating their own mate values in the adolescence phase of the mating process. We have found that the estimation errors attain their lowest values under Mate Value-5, while they are in general lower under Adjust Relative/2 than under the other realistic rules, namely Take the Next Best, Adjust Up/Down, and Adjust Relative. In addition, the estimation errors under Adjust Relative/2 are as low as they are under the unrealistic rule of Mate Value-5 when the adolescence length is medium to long. This is quite puzzling given the huge difference between the mating likelihoods generated by these two heuristics always in favor of Mate Value-5. However, this puzzle vanishes away once we calculate the mean aspiration levels of all individuals. Whereas under Mate Value-5 the mean aspiration level is —by definition— lower than the mean mate value of the population by the value of 5, it is approximately equal to the mean mate value under Adjust Relative/2. This finding indicates that the success of a heuristic may not only be related to the precision or correctness of individuals in estimating their own mate values in the adolescence phase but also to their humbleness in making their estimations.
To realize our second object —the finding of a plausible heuristic that is comparable to Mate Value-5 and superior to any realistic search rule of Todd and Miller (1999) in terms of mating likelihood— we have proposed a search rule, called Take the Weighted Average with the Next Desiring Date TWAND. Our simulations using this search rule have revealed that in terms of the mating likelihood TWAND is outstandingly superior to all realistic search rules of Todd and Miller (1999), including Adjust Relative/2. Moreover, the overall performance of TWAND and the unrealistic rule of Mate Value-5 are very close. While Mate Value-5 dominates TWAND for short to medium adolescence lengths, TWAND becomes superior to Mate Value-5 when the adolescence length is long. Clearly, this is a downside of TWAND since in reality longer adolescence lengths imply higher costs —for individuals seeking mates— in terms of time, effort, and/or money.
Our simulations have also revealed that our new search heuristic TWAND is superior to all search rules of Todd and Miller (1999) in terms of time to pair. In addition, in terms of mating balancedness/egalitarianism it performs better than some search rules of Todd and Miller (1999), including Take the Next Best, Adjust Up/Down, and Adjust Relative. However, TWAND has an undesirable implication as well. With respect to a notion of stability, measured by the mean within-pair difference in mate value, TWAND always performs worse than any heuristic of Todd and Miller (1999). When individuals become extremely willing to pair up with individuals whose mate values are below their own mate values, they increase not only their likelihood and speed of mating but also the likelihood that they will divorce in the future.
To understand the secret behind the success of TWAND in terms of mating likelihood and mating speed, we have calculated the corresponding root mean square error made by all individuals in estimating their own mate values. We have found that RMSE for TWAND is higher than RMSE for any search rule of Todd and Miller (1999), except for Take the Next Best. This shows that the success of TWAND in terms of mating likelihood cannot be attributed to the precision of information individuals obtain about their own mate values. As we have suspected that this success is caused by the direction of estimation errors made by individuals, we have also calculated the mean aspiration levels of all individuals at the end of the adolescence phase for all search rules studied in this paper. Interestingly, we have found that the mean aspiration level of all individuals always attains its lowest value under TWAND, implying that this heuristic is even more humble than the most humble (but unrealistic) heuristic of Todd and Miller (1999), namely Mate Value-5. It is also worth noting that the humbleness of TWAND does not come up with a pre-determined constant like in the case of the Mate Value-5 rule. Instead, it comes with an endogenously determined aspiration threshold which indirectly takes the mate value (self image) of the individual into account, so that the less valuable an individual is, the less choosy he/she becomes during the mating phase. In fact, just because of this TWAND is more likely —and also needs less interactions— to pair up individuals than any realistic search rule of Todd and Miller (1999).
Finally, we should note that one shortcoming of our paper (and also the paper of Todd & Miller, 1999) is that all individuals in the mating population are assumed to use the same search strategy. This assumption can be problematic because a strategy a which may have a worse performance than some other strategy b —according to some success measure— when the whole mating population uses the same strategy might in fact have a better performance if it were used only by a sufficiently small part of the population while the rest of the population remained to use strategy b. In that case, a possibility where each individual in the mating population uses strategy b cannot be an equilibrium situation, since some group of individuals would have incentives to deviate from strategy b to strategy a. This particular problem of robustness was recently studied —as mentioned earlier in this paper— by Saglam (2014), who investigated whether the use of any strategy of Todd and Miller (1999) by the whole population can arise as a Nash equilibrium situation, where no individual has an incentive to unilaterally deviate from the strategy the rest of the population —he/she believes— will use. Future research may profitably use the analysis of Saglam (2014) to check whether the mate search strategy proposed in our paper, TWAND, is evolutionarily stable/robust against the mate search strategies of Todd and Miller (1999), and vice versa.
Footnotes
1.
On the other hand, for one-sided sequential mate search it is well known that there exists an optimal search rule requiring any individual to screen exactly 37% of the potential mates, to set his/her aspiration level to the highest observed mate value at this screening stage, and to choose the first potential mate with a mate value higher than this aspiration (Ferguson, 1989).
2.
Note that the choice of the adjustment constant
3.
The mating likelihood under Mate Value-5 is decreasing in the number of dating interactions even though the aspirations of individuals are constant during the mating process. This is due to the fact that in the mating phase individuals cannot interact with their dates in the adolescence phase. When the number of dating interactions becomes higher, for each individual the number of potential mates that can be checked in the mating phase becomes lower, consequently lowering for all individuals the chance of meeting a mutually acceptable mate.
4.
Also, one can show that both the top 5 percent and the bottom 5 percent of the population are —as a whole— mutually agreeable to 7.5 percent of the potential mates. Given the fact that each individual in the rest of the population (i.e., the other 90 percent) is mutually agreeable to 10 percent of the potential mates, one can easily calculate that an individual —on average— is mutually agreeable to 9.75 (=0.9 x 10 + 0.1 x 7.5) percent of the potential mates.
5.
On the other hand, if the mate values of all males and females were drawn from the same continuous distribution, Mate Value-0 would yield a likelihood of mating as low as 0 percent.
References
- 1
-
2
Learning rules for optimal selection in a varying environment: Mate choice revisitedBehavioral Ecology 17:799–809.
-
3
On adaptive search and optimal stopping in sequential mate choiceAmerican Naturalist 144:355–361.
- 4
-
5
Adaptive search and information updating in sequential mate choiceAmerican Naturalist 148:123–137.
-
6
Equilibrium points in n-person gamesProceedings of the National Academy of Sciences 36:48–49.
-
7
Simple heuristics as equilibrium strategies in mutual sequential mate searchJournal of Artifcial Societies and Social Simulation 17:12.
-
8
Analysis of asymmetric two-sided matching: Agent-based simulation with theoremproof approachJournal of Artifcial Societies and Social Simulation 16:11.
-
9
Simulating Social Phenomena419–436, Searching for the next best mate, Simulating Social Phenomena, Berlin, Springer-Verlag.
-
10
Simple Heuristics That Make Us Smart287–308, From pride and prejudice to persuasion: Satisficing in mate search, Simple Heuristics That Make Us Smart, (p., New York, Oxford University Press.
Article and author information
Author details
Acknowledgements
The author is grateful to two anonymous reviewers for very detailed and helpful comments and suggestions which have greatly improved this paper. The usual disclaimer applies.
Publication history
- Version of Record published: August 31, 2018 (version 1)
Copyright
© 2018, Saglam
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.