Combining Microsimulation and Numerical Maximization to Identify Optimal Tax-Transfer Rules

Cite this article as: U. Colombino, N. Islam; 2022; Combining Microsimulation and Numerical Maximization to Identify Optimal Tax-Transfer Rules; International Journal of Microsimulation; 15(2); 4-43. doi: 10.34196/ijm.00261

Article
Figures and data
Jump to

Abstract

In this paper we propose a computational approach to empirical optimal taxation. We develop and estimate a microeconometric model that is run to simulate household labour supply decisions and the implied economic, fiscal and welfare effects. The microsimulation is embedded into a numerical optimization routine that identifies the tax-transfer rule that maximizes a social welfare function. We consider the class of tax-transfer rules where net available income is computed as a 4th degree polynomial transformation of taxable income plus a transfer. We present the results for six European countries: Germany, France, Italy, Luxembourg, Spain and the United Kingdom. For most values of the inequality aversion parameter k that characterizes the social welfare function, the optimized rules provide a higher social welfare than the current rule, with the exception of Luxembourg. The optimized tax-transfer rules are close to a Flat Tax plus a Universal Basic Income (or equivalently a Negative Income Tax).

1. Introduction

One of the most popular uses of microsimulation is the evaluation of tax-transfer reforms. In this paper we propose it as a tool to attain a more general goal, namely the identification of an optimal Tax-Tranfer Rule (TTR).

In the basic framework of optimal taxation theory, the Government chooses the taxes to be applied to household personal incomes with the aim of maximizing some social welfare criterion that accounts for both total welfare and its distribution among the households. While doing so, the Government takes into account a public budget constraint - i.e. taxes net of transfers must collect a given amount (to be used in public expenditures) – and an incentive constraint, i.e. household taxable incomes (and therefore taxes computed according to the TTR) are determined by household (utility maximizing) choices subject to household budget constraints.

The relevance of the solution to the above problem for the policy implementation critically depends on the flexibility and generality of the assumptions.

The analytical optimal taxation, pioneered by Mirrlees (1971), is a fundamental contribution since it sets the basic problem to be solved. Its empirical applications (e.g. Mirrlees, 1971; Tuomala, 1990; Tuomala, 2009; Saez, 2001) can also indicate promising directions of policy reform. However, it suffers from various limitations. First, Mirrlees (1971) and Saez (2001) consider only intensive labour supply. Saez (2002) presents a model that accounts for extensive responses under very special restrictive assumptions. Second, the implications of household simultaneous decisions are typically ignored. Third, the individual skill is unidimensional. Fourth, it ignores non-standard, though important, features of household choice sets such as frictions and quantity constraints.

Saez (2001) introduced a reformulation of the analytical approach that apparently overcomes some of the above limitations and promises to compute optimal taxes based only on observables or non-parametric estimates (thus dispensing with strong structural assumptions) – an approach that Chetty (2009) generalized and labelled as the “Sufficient Statistics” approach. However, when it comes to computing optimal TTRs, in general this approach can only provide local approximations: if what we want is a global solution for optimal TTRs, in general we must still assume a specific labour supply model, i.e. some structural specification that produces labour supply decisions given households’ preferences and budget constraints (Saez, 2001; Brewer et al., 2008).

Under a different perspective, the analytical approach might be too general. No a-priori parametric class of rules is chosen. In practice, however, the results typically boil down to a rule that can be easily approximated by a polynomial. Giving up some of the generality on the side of the TTR, permits more generality and flexibility on the side of the representation of agents, preferences, constraints and behaviour.¹

With the approach adopted in this paper, besides considering a parametric class of TTRs, we analyse both single and couples, account for both extensive and intensive responses, multidimensional source of welfare and specify a flexible utility maximization framework with heterogeneous preferences and constraints.

Our main research purpose is a methodological one and consists of developing and illustrating a consistent computational approach to empirical optimal taxation that can usefully complement the traditional analytical approaches.

The background of the computational approach is exemplified by a series of papers: Islam and Colombino (2018) identify optimal TTRs within the class of Negative Income Tax rules cum Flat Tax (NIT+FT) in eight European countries. Aaberge and Colombino (2006) and Aaberge and Colombino (2013) identify optimal taxes for Norway within the class of 9-parameter piece-wise linear TTRs. Aaberge and Colombino (2012) perform a similar exercise for Italy. Blundell and Shephard (2012) design an optimal TTR for lone mother in the UK. Closely related contributions are Fortin et al. (1993), Sefton and Van De Ven (2009), Creedy and Herault (2011) and Colombino (2015).

We consider the class of TTRs defined by a 4^th degree polynomial, i.e. net income is computed as 4^th degree polynomial of taxable income plus a constant that depends on household’s size. Even though it is a parametric representation, it is flexible enough to be judged close to a non-parametric rule. A micro-econometric model simulates the utility maximizing household choices given any member of the polynomial class of TTRs. The microsimulation is embedded into a constrained optimization algorithm that solves the social planner’s problem, i.e. the maximization – with respect to the parameters of the polynomial TTR – of a social welfare function subject to the public budget constraint. This procedure solves the same problem addressed by the analytical approach, but it permits to adopt more general assumptions concerning preferences, opportunity sets and constraints.

Our second research purpose – a substantive one – consists of investigating the feasibility and the social welfare performance of a simple and universalistic TTR. Most of the quantitative analysis of tax-transfer reforms in the last three decades are dedicated to mean-tested, targeted and categorical policies, which are also the prevailing policies in the considered countries. The policy debate, however, considers also an alternative direction of reform that aims at over-coming (or complementing) means-testing and categorical policies, pointing towards universality, unconditionality and simplicity.² In this paper, by adopting the polynomial TTR as a universal rule, we follow this latter alternative view.

This paper contributes to the literature along three dimensions.

First, on the methodological side, with respect to the previous papers adopting a computational approach, the paper considers a much larger and flexible class of TTRs, develops an explicit procedure that consistently integrates numerical optimization and microsimulation, considers the whole (potentially) active population (including couples, singles, wage employed and self-employed) and produces results for six European countries. Islam and Colombino (2018) limit their exercise to the Negative Income Tax with Flat Tax. Aaberge and Colombino (2006), Aaberge and Colombino (2012) and Aaberge and Colombino (2013) work on one country and adopt a more restrictive class of TTRs. Blundell and Shephard (2012) consider one country and only a specific segment of the population.

Second, on the substantive side, the paper shows that for most degrees of social aversion to inequality, the optimized polynomial TTRs provide a higher social welfare than the current rule, with the exception of Luxembourg. The optimized TTRs are close to a (almost) Flat Tax (FT), with a Universal Basic Income (UBI) or – equivalently – a Negative Income Tax (NIT).

Third, we identify some significant effects of “primitives” (i.e., basic characteristic of the economy) on the features of the optimal polynomial TTRs. Despite the common features, the results show also large differences in the different countries. They depend indeed on various characteristics of the population and of the economic environment. An explanation of these differences requires to identify a general relationship between the basic (“primitive”) characteristics of the economy and the features of the optimal TTRs. Actually, this is the direct result of analytical optimal taxation. We can come close to a similar result by identifying a “mapping” from the set of country-specific “primitives” to the set of country-specific optimal TTRs.

Section 2 and 3 provide a summary presentation of the analytical approach and of the computational approach. Section 4 contains a detailed explanation of the procedure implemented in order to identify the optimal country-specific TTRs and the mapping from the “primitives” to the features of the optimal TTRs. Section 5 illustrates the results and Section 6 concludes. The Appendix reports the country-specific estimates of the microeconometric model for couples and singles.

2. The analytical approach

The analytical approach, pioneered by Mirrlees (1971), can be summarized as follows. It assumes a population of individuals (the “agents”) with identical preferences and different skill (or productivity) n with distribution function F(n) and probability density function f(n). A utility function U(C, e) represents the individual preferences, where C = income and e = “effort” (or labour supply). The Government (i.e. the “principal”) solves

\begin{matrix} max_{T (.)} \int_{0}^{\infty} S (U (n e_{n} - T (n), e_{n})) f (n) d n \\ s . t . \\ \int_{0}^{\infty} T (n) f (n) d n \geq R \\ e_{n} = \arg \max_{e} u (n e - T (n), e) \end{matrix}

S(.) is a social welfare function and T(.) is a TTR that must be determined optimally.The first constraint is the public budget constraint, where R is the average tax revenue to be collected. The second constraint – the so-called Incentive Compatibility Constraint – says that e_n is the effort level that maximizes the utility of the agent with productivity n.

Mirrlees (1971) solves problem (1) with optimal control techniques. As a simple example, by assuming a quasi-linear U(.) – i.e. no income effects – one can obtain:

\begin{matrix} \frac{T ` (n)}{1 - T ` (n)} = (1 + \frac{1}{η}) (\frac{1 - F (n)}{n f (n)}) (1 - G (n)) \\ T_{0} = \int_{0}^{\infty} T (n) d F (n) - R \end{matrix}

where T’(n) is the marginal tax rate (MTR) applied to agents with productivity n (who have income ne_n), G(n) is a social weight that depends on S() and U() and is assigned to individuals with productivity greater than or equal to n and η denotes the elasticity of e with respect to n. $T_{0}$ is a transfer paid to individuals with no income.

It is common to label U(.), S(.), F(.), f(.), η and R as the “primitives” (or the basic characteristics of the economy). For any given set of “primitives” there is a corresponding optimal TTR. The empirical applications consist of computing optimal policies using formulas such as expression 2 – or generalizations of it – with imputed or calibrated “primitives”.

In Mirrlees’ original formulation, n and e are not directly observed by the Government, who is constrained to tax income ne_n. When it comes to empirical applications, n might be equated to the wage rate or imputed with a calibration procedure (e.g. Brewer et al., 2008). By assuming an explicit utility function U(C, e) and using $e_{n}=argmax_{e}U\left (ne- T\left (n\right),e\right)$ one can compute the gross income ne_n and write expression in terms of gross income.

Saez (2001; 2002) presents a reformulation the Optimal Taxation problem (known as “sufficient statistics” approach after Chetty (2009)) where expressions similar to 2 can be obtained by a “perturbation” method, i.e. working out the total effect of a marginal change of taxes and setting it equal to zero at the optimum. The solution can be expressed solely in terms of directly observed variables and non-parametrically estimable parameters (the “sufficient statistics”). As an example, in Saez (2001), under appropriate conditions, the following expression is obtained:

\frac{T ` (z)}{1 - T ` (z)} = (\frac{1}{η_{z}}) (\frac{1 - H (z)}{z h (z)}) (1 - Π (z))

where z denotes taxable income, h(z) and H(z) are the density and distribution functions, $\Pi \left (z\right)$ is a social weight assigned to people with income greater than or equal to z and $\eta _{z}$ is the elasticity of z with respect to (1-T’(z)).

Expression 3 is obtained without explicit structural assumptions about preferences nor about the link between the TTR, T(.) and z. However, expression 3 is a “snapshot” of the optimal solution and – except for special cases – does not permit to compute directly the optimal taxes. The optimal z and its distribution (and possibly also $\eta _{z}$ ) depend on the optimal tax function $T\left (.\right)$ . Therefore, in order to be able to compute the optimal taxes we must specify how z, H(z) and h(z) depend on $T\left (.\right)$ . In other words, we must go back to Mirrlees (1971), as in Saez (2001) and Brewer et al. (2008), or introduce some ad hoc assumptions as in Saez (2002). A recent paper by Kleven (2021) clarifies the limitations of the “sufficient statistics” approach and confirms that extending it in order to overcome those limits essentially brings it back to a structural approach, i.e. an explicit specification of households’ preferences and constraints.

3. The computational approach

Modern micro-econometric models of labour supply can be specified according to very general and flexible assumptions. They can account for many realistic features such as heterogeneous preferences, jobs and opportunity sets, simultaneous decisions of couples, complicated budget constraints, quantity constraints, etc. It might not be feasible or practical to obtain analytical solutions for the optimal taxation problem in such economic environments. Yet those features are likely to be relevant and important for evaluating or designing reforms. The ability to adopt more general assumptions might lead to design more robust policy prescriptions.

The implementation of the computational approach consists of the following operations.

First, we develop and estimate a microeconometric model of household labour supply. The model accounts for both singles and couples, wage employed, self-employed and non-participants, extensive and intensive labour supply responses, heterogeneous preferences and quantity constraints (i.e. different availability of different types of jobs).

Second, given a member of the polynomial class of TTRs, we can simulate household choices based on the estimated household preferences and compute the attained value of household utility. The simulation is embedded into an iterative maximization algorithm in order to identify the TTR that maximizes a Social Welfare function. The Social Welfare function takes as arguments (an appropriate transformation of) the previously computed household utility level.³

At this point we have identified a specific optimal polynomial TTR for each country. Given the country-specific optimal TTRs and a set of country-specific “primitives” (i.e. basic characteristics of the economy) we can then identify the mapping from the “primitives” to the optimal TTRs, i.e. a general rule analogous to the one identified by the analytical approach.⁴ As a matter of fact, the path of the computational approach is opposite to path of the analytical approach. The latter solves for a general rule and then can obtain country-specific rules by assigning country-specific values to the “primitives”. The former identifies country-specific rules from which a general rule can be inferred. The general rule can be used for many purposes, e.g. providing indications for tax reforms in countries where reliable or sufficiently detailed micro data are not available; making out-of-sample predictions in order to test the whole optimal taxation procedure; forecasting the need for fiscal reforms based on predictions about trends or future changes of the “primitives”.

4. Implementing the computational approach

This section provides details upon the various steps of the computational approach.

4.1. The microeconometric model

The household opportunity set contains jobs or activities characterized by hours of work h, sector of market job s (wage employment or self-employment) and other characteristics (observed by the household but not by us). We define h as a vector with one element for the singles and two elements for the couples, $\mathbf{h}=\left (\begin{array}{c}h_{M}\\h_{F}\end{array}\right)$ , where the subscripts F and M refer to the female and the male partner respectively. Analogously, in the case of couples, $\mathbf{s}=\left (\begin{array}{c}s_{M}\\s_{F}\end{array}\right)$ . The household-specific wage vector is $\mathbf{w}_{\mathbf{i}}=\left (\begin{array}{c}w_{iM}\\w_{iF}\end{array}\right)$ . Each household member can work only in one sector.

The opportunity set for singles contains 7 alternatives,

\begin{matrix} (0, 0), \\ (s = 1, 0 §lt; h \leq 26), \\ (s = 2, 0 §lt; h \leq 26), \\ (s = 1, 26 §lt; h \leq 52), \\ (s = 2, 26 §lt; h \leq 52), \\ (s = 1, 52 §lt; h \leq 80), \\ (s = 2, 52 §lt; h \leq 80) . \end{matrix}

where (0,0) denotes a non-market “job” or activity (non-participation, job search etc.). For each household, the values of h are drawn from the observed distribution of hours in each hour interval 1-26 (part time), 27-52 (full time), 52-80 (extra time) and the sector indicator s is equal to 0 (non-market activity) or 1 (wage employment) or 2 (self-employment). For couples, the household opportunity set is the Cartesian product of two single opportunity sets and contains 49 alternatives.

The systematic utility function is specified as follows (for couples), where j indexes the 49 job types:

\begin{array}{ll} V_{i} (j; w_{i}, τ) & = γ_{1} C_{j} + γ_{2} (C_{j})^{2} + γ_{3} C_{j} \times N_{i} \\ + λ_{1} L_{j M} + λ_{2} (L_{j M})^{2} + λ_{3} L_{j F} + λ_{4} (L_{j F})^{2} \\ + λ_{5} L_{j M} \times C_{j} + λ_{6} L_{j F} \times C_{j} \\ + λ_{7} L_{j M} \times A_{i M} + λ_{9} L_{j F} \times A_{i F} \\ + λ_{8} L_{i M} \times (A_{i M})^{2} + λ_{10} L_{i F} \times (A_{i F})^{2} \\ + λ_{9} L_{j M} \times K_{i 0} + λ_{11} L_{j F} \times K_{i 0} \\ + λ_{12} L_{j M} \times K_{i 6} + λ_{13} L_{j F} \times K_{i 6} + λ_{14} L_{j M} \times K_{i 10} + λ_{15} L_{j F} \times K_{i 10} \end{array}

where C_ji = net disposable income at job j given wage w_i and unearned income I_i under TTR τ. It results from applying the TTR to the total household taxable income $y_{ji}=\mathbf{w}_{ji}^{`}\mathbf{h}_{ji}+I_{i}- \text{SSC}_{ji}$ , where $\text{SSC}_{ji}$ denotes social security contributions;

L_jM = leisure time at job j of the head-of-household;
L_jF = leisure time at job j of the partner;
N_i = number of household components;
A_iM = age of the head-of-household;
A_iF = age of the partner;
K_i0 = 1 if no children belong to the household (= 0 otherwise)
K_i6 = number of children in age <= 6;
K_i10 = number of children in age > 6 and <= 10.

For single households, only the terms for a single person are present.

When computing the earnings of any job (s, h) we face the problem that the wage rates of sector s are observed only for those who work in sector s. Moreover, for individuals who are not working we do not observe any wage rate. To deal with this issue, we follow a two-stage procedure presented in Dagsvik and Strøm (2006) and adopted also by Coda Moscarola et al. (2020). The procedure is analogous to the well-known Heckman correction for selectivity but is specifically appropriate for the distribution assumed for $\varepsilon$ .

The dummy variables D that are used to represent the availability of the various job-types are specified as follows.

Single households:

\begin{matrix} D_{1, 0} = 1 [s = 1, h §gt; 0], \\ D_{2, 0} = 1 [s = 2, h §gt; 0], \\ D_{1, 1} = 1 [s = 1, 0 §lt; h \leq 26], \\ D_{2, 1} = 1 [s = 2, 0 §lt; h \leq 26], \\ D_{1, 2} = 1 [s = 1, 26 §lt; h \leq 52], \\ D_{2, 2} = 1 [s = 2, 26 §lt; h \leq 52] . \end{matrix}

Couple households:

\begin{matrix} D_{M, 1, 0} = 1 [s_{M} = 1, h_{M} §gt; 0], \\ D_{M,}_{1, 1} = 1 [s_{M} = 1, 0 §lt; h_{M} \leq 26], \\ D_{M, 1, 2} = 1 [s_{M} = 1, 26 §lt; h_{M} \leq 52], \\ D_{M, 2, 0} = 1 [s_{M} = 2, h_{M} §gt; 0], \\ D_{M, 2, 1} = 1 [s_{M} = 2, 0 §lt; h_{M} \leq 26], \\ D_{M, 2, 2} = 1 [s_{M} = 2, 26 §lt; h_{M} \leq 52] \\ D_{F, 1, 0} = 1 [s_{F} = 1, h_{F} §gt; 0], \\ D_{F,}_{1, 1} = 1 [s_{F} = 1, 0 §lt; h_{F} \leq 26], \\ D_{F, 1, 2} = 1 [s_{F} = 1, 26 §lt; h_{F} \leq 52], \\ D_{F, 2, 0} = 1 [s_{F} = 2, h_{F} §gt; 0], \\ D_{F, 2, 1} = 1 [s_{F} = 2, 0 §lt; h_{F} \leq 26], \\ D_{F, 2, 2} = 1 [s_{F} = 2, 26 §lt; h_{F} \leq 52] . \end{matrix}

where 1[.] is the indicator function.

We estimate the labour supply models of couples and singles separately. For singles, the probability of willing to hold a job of type (s, h) is:

P_{i} ((s, h); w_{i}, τ) = {\begin{cases} \frac{e x p {V_{i} ((s, h); w_{i}, τ) + \sum_{t = 1}^{2} \sum_{u = 0}^{u} δ_{t, u} D_{t, u}}{\sum_{s}^{} \sum_{h}^{} e x p {V_{i} ((s, h); w_{i}, τ) + \sum_{t = 1}^{2} \sum_{u = 0}^{2} δ_{t, u} D_{t, u}}} \end{cases}

For couples, the probability of willing to hold a job of type $\left (s,h\right)=\left (s_{M},s_{F},h_{M},h_{F}\right)$ is:

P_{i} ((s, h); w_{i}, τ) = {\frac{\exp {V_{i} ((s, h); w_{i}, τ) + \sum_{g = M}^{F} \sum_{t = 1}^{2} \sum_{u = 0}^{2} δ_{g, t, u} D_{g, t, u}}}{\sum_{s}^{} \sum_{h}^{} \exp {V_{i} ((s, h); w_{i}, τ) + \sum_{g = M}^{F} \sum_{t = 1}^{2} \sum_{u = 0}^{2} δ_{g,t,u} D_{g,t,u}}}

The model is a simplified version of the so-called RURO model.⁵ The main simplification concerns the wage rates. In the most general versions of the RURO model the wage rates densities are estimated simultaneously with the preference parameters and the hours’ opportunity density. In this paper we use instead pre-estimated wage densities.

Expressions 8 and 9 are the contribution to the likelihood function to be maximized in order to estimate the parameters γ, λ and δ.

The datasets used in the analysis are the EUROMOD input data based on the European Union Statistics on Income and Living Conditions (EU-SILC 2015) for France,⁶ Italy, Germany, Luxembourg, Spain and on the Family Resources Survey (FRS 2015) for the United Kingdom. The input data provide all the required information on demographic characteristics and human capital, employment and wages of household members, as well as information about various sources of non-labour income. We apply common sample selection criteria for all the countries under study by selecting individuals in the age range 18-55 who are not retired or disabled. EUROMOD⁷ is used for two different operations. First, for every household in the sample, it computes the net available income under the current TTR at each one of the 49 (7) alternatives available to the couples (singles). The net available incomes are used in the estimation of the labour supply model. Second, for each household, it computes the gross income at each alternative. Gross incomes are used in the simulation and optimization steps, where EUROMOD is not used anymore and new values of net available incomes are generated by applying the new TTRs to the gross incomes.

The estimates of the model are reported in tables A1–A12.

4.2. The class of polynomial TTRs

We look for optimal TTRs within the class of rules defined as a polynomial functions of total household taxable income $y_{i}=\mathbf{w}_{i}^{`}\mathbf{h}_{i}+I_{i}- \text{SSC}_{i}\text{.}$ Net available income C_i is specified as follows:

C_{i} = τ_{0} \sqrt{N_{i}} + τ_{1} y_{i} + τ_{2} y_{i}^{2} + τ_{3} y_{i}^{3} + τ_{4} y_{i}^{4}

where $y_{i}$ (= total taxable household income) and $N_{i}$ = household size. The choice of this simple specification is due to three main motivations. First, since we compare six different countries, our results are made more easily interpretable by abstracting from details and keeping the optimal TTRs as simple as possible. Second, even though the 4^th degree polynomial specification is parametric, it is flexible enough to be judged close to a non-parametric rule. Third, we are interested in investigating whether a very simple and universalistic TTR can be social-welfare-superior to the (typically means-tested, categorical and complex) current TTRs.

The corresponding TTR is:

T (y_{i}; τ) = y_{i}^{} - τ_{0} \sqrt{N} - τ_{1} y_{i} - τ_{2} y_{i}^{2} - τ_{3} y_{i}^{3} - τ_{4} y_{i}^{4}

The marginal tax rate and the average tax rate are respectively:

\begin{matrix} M T (y; τ) = \frac{\partial T (y; τ)}{\partial y} = 1 - τ_{1} - 2 τ_{2} y^{} - 3 τ_{3} y^{2} - 4 τ_{4} y^{3} \\ A T (y; τ) = \frac{T (y; τ)}{y} = 1 - \frac{τ_{0} \sqrt{N}}{y} - τ_{1} - τ_{2} y^{} - τ_{3} y^{2} - τ_{4} y^{3} \end{matrix}

The rule is sufficiently flexible to represent many alternative versions of TTRs. Provided $\tau _{0}§gt;0$ , the rule can be interpreted as a negative income tax or a UBI matched with a generic tax rule.⁸ In the former case $\tau _{0}\sqrt{N_{i}}$ is the universal guaranteed minimum income when $y_{i}=0$ , in the latter case it is a universal basic income. The case $C_{i}=\tau _{0}\sqrt{N_{i}}+\tau _{1}y_{i}$ , therefore, corresponds to a unconditional basic income with flat tax (UBI+FT) or, equivalently, to a negative income tax with flat tax (NIT+FT). The term $\sqrt{N_{i}}$ rescales the guaranteed minimum income or the basic income according to the household size (square root rule). A pure flat tax rule is the special case $C_{i}=\tau _{1}y_{i}.$ Also rules with negative marginal taxes (such as In-work Benefits or Tax Credits) are accounted for, depending on the values of the parameters τ.

When identifying the optimal TTR, the rule of expression completely replaces the current TTR.

Although being able to generate many different shapes of the tax profile, our class of candidate TTRs is admittedly very simple with respect to three dimensions. First, it is universal, i.e. - with the exception of the equivalence scale applied to the parameter τ₀ - it does not discriminate on the basis of personal characteristics. Second, the rule of expression 10 applies to the sum of all household personal taxable incomes, whatever the source; the current TTRs might instead use different rules depending on the source and might apply differently to individual or household incomes. Third, the current income support mechanisms are typically a combination of (mostly) means-tested and categorical/targeted transfers. The rule of expression 10, instead, envisages a universal mechanism that can be interpreted as a guaranteed minimum income or as a basic income, provided τ₀> 0. The heterogeneity accounted for in the data and in the microeconometric model in principle might allow us to consider TTRs based on some categorical/targeted articulation of tax rates and subsidies, which might be welfare-superior to our optimal polynomial TTRs. However, categorical/targeted and complex means-tested designs of the TTR bear administrative and political costs that are instead smaller or even non-existent in simple and universalistic designs. In view of policy reforms, it is interesting to test the performance of a very simple, transparent and universalistic TTR against the current (typically categorical/targeted and means-tested) TTR.

A correct interpretation of the comparison of the optimal TTR to the current one must take into account the important differences mentioned above. In the evaluation of the relative performance of the optimal polynomial TTRs as compared to the current TTRs, we can only conclude that a certain TTR is better or worse (according to a given criterion) than another one. We cannot identify the specific contribution of, say, income support mechanisms, or the treatment of different income sources, to the relative performance of optimal TTRs as compared to current TTRs. However, as an aid to comparing the current TTR to the optimized TTRs, we also compute a polynomial approximation to the current TTR, which in some sense provides a view of the current TTR through the “lens” of the polynomial class. The approximation is the 4^th degree polynomial that satisfies the public budget constraint and minimizes the sum of squared differences between the household observed disposable income and the household disposable income computed according to expression. The approximation is not used to produce the welfare and economic effects of the current TTR, which are instead the real ones produced by the real current TTR.

4.3. Welfare evaluation

We define the Comparable Money-metric Utility (CMU). This concept is based on the approach proposed by King (1983), where different preferences are due to different characteristics within a common parametric utility function. The characteristics account for a different productivity in obtaining utility from the opportunities available in the budget set. The utility levels attained by households with different preferences are made comparable by using a common “reference” household. The CMU of a given household i is the level of income that the “reference” household would need to attain the same utility level attained by household i. The procedure is analogous to using a reference price vector in order to compare utility levels attained under different price vectors. Empirical examples of this approach are provided by King (1983), Aaberge et al. (2004) and Islam and Colombino (2018). Our CMU transforms the household utility level into an inter-household comparable monetary measure that will enter as argument of the Social Welfare function. First, we calculate the expected maximum utility attained by household i under tax-transfer regime $\tau$ (McFadden, 1978): $ln\left (\underset{j}{\sum }exp\left \{V_{i}\left (j;w_{i},\tau \right)\right \}\right)$ . Analogously, we define $ln\left (\underset{j}{\sum }exp\left \{V_{R}\left (j;w_{R},\tau _{R}\right)\right \}\right)$ as the expected maximum utility attained by the “reference” household R under the “reference” tax-transfer regime $\mathbf{\tau }_{R}$ . The reference household is the couple household at the median value of the distribution of the expected maximum utility. The reference TTR $\mathbf{\tau }_{R}$ is a pure flat tax that satisfies the public budget constraint. The CMU of household under tax regime $\mathbf{\tau }$ , $\mu _{i}\left (\mathbf{\tau }\right)$ , is defined as the gross income that a reference household under a reference tax-transfer regime $\mathbf{\tau }_{R}$ would need in order to attain the same expected maximum utility obtained by household i under TTR $\mathbf{\tau }$ (Colombino, 2021). Although the choice of the reference household is essentially arbitrary, some choices make more sense than others. Our choice of the median household as the reference household can be justified in terms of representativeness or centrality of its preferences.

i

In order to aggregate the household-specific welfare levels, we choose the Social Welfare index proposed by Kolm (1976), which can be defined as:

W = \bar{μ} - \frac{1}{k} ln [\sum_{i} \frac{exp {- k (μ_{i} - \bar{μ})}}{N}]

W has limit $\bar{\mu }$ as $k\rightarrow 0$ and $min\left \{\mu _{1},...,\mu _{N}\right \}$ as $k\rightarrow \infty$ .

$\bar{\mu }=\frac{1}{N}\underset{i}{\sum }\mu _{i}\text{\ }$ is an index of efficiency

\frac{1}{k} \ln [\sum_{i} \frac{\exp {- k (μ_{i} - \bar{μ})}}{N}] = Kolm’s Inequality Index

$k=$ inequality aversion parameter⁹

μ_i = comparable money-metric utility of household i .

Therefore, Social Welfare = Efficiency – Inequality. Social Welfare and its components are monetary measures. The Inequality Index can be interpreted as the cost of inequality.¹⁰

4.4. Identification of optimal TTRs

The problem to be solved can be written as follows:

\begin{matrix} max_{τ} W (μ_{1} (τ), ..., μ_{H} (τ)) \\ s .t . \\ \sum_{i}^{} \sum_{j} P_{i j} (τ) T_{i j} (τ) \geq R \end{matrix}

where $P_{ij}\left (\mathbf{\tau }\right)$ is the probability that household i chooses alternative j under TTR $\mathbf{\tau }$ (according to expressions -) and $T_{ij}\left (\mathbf{\tau }\right)$ is the net tax paid by household i when choosing alternative j under TTR $\mathbf{\tau }$ . The constraint requires that the total expected net tax revenue be greater than (or equal to) a given amount R. Note that problem assumes that the households are maximizing their utility functions, since the arguments of W are the (comparable money-metric) maximized utilities. The problem is solved with a numerical procedure. Given a vector of parameters $\mathbf{\tau }$ , the microeconometric model simulates $\mu _{i}\left (\mathbf{\tau }\right)$ , $P_{ij}\left (\mathbf{\tau }\right)$ and $T_{ij}\left (\mathbf{\tau }\right)$ for i = 1,…,H (number of households) and j = 1,…,M (number of alternatives in the opportunity set). An optimization algorithm iterates the above simulation updating the value of the parameter vector $\mathbf{\tau }$ until W cannot be further improved.¹¹

4.5. From the “primitives” to the optimal polynomial TTRs

The analytical optimal taxation identifies general TTR as a function of generic exogenous parameters π called “primitives”, i.e. fundamental exogenous characteristics of the economy: $TTR=f\left (\mathbf{\pi }\right).$ In order to specify the optimal TTR for a specific country c , the analytical approach imputes to the primitives the country-specific values $\pi _{c}$ in order to get $TTR_{c}=f\left (\mathbf{\pi }_{c}\right).$ With the computational approach, we can follow the inverse path. First, we identify $τ_{c}$ , c = 1, 2, …, T, for T countries. Then we can retrieve a mapping $(π_{1}, π_{2}, \dots, π_{T}) \to (τ_{1}, τ_{2}, \dots, τ_{T})$ . Our small sample six countries allows us to present only an illustrative example that uses regression analysis. We consider the following “primitives”.

Kolm’s k. The inequality aversion parameter k, multiplied by 100. As a matter of fact, we have six different values of k for each one of the six countries, which makes 36 observations.
Productivity. The current average monthly taxable household income, as a measure of productivity.
Extensive Elasticity. The average participation elasticity with respect to the wage rate.
Intensive Elasticity. The average hours elasticity with respect to the wage rate.
Budget. The current monthly net tax revenue to be attained in order to satisfy the public budget constraint.¹²

We characterize the optimal TTRs with:

τ₀. This is the UBI or the guaranteed minimum income in a NIT rule.
100(1-τ₁). This is the percentage Leading Tax Rate. The definition is motivated by the fact that the other tax parameters τ₂, τ₃ and τ₄ - as we will show in Section 5 – are very small and have a sensible effect only at very high levels of taxable income.

Notice that the higher τ₀ and the lower 1-τ₁, the larger is the range of taxable income with negative net taxes, therefore the ratio τ₀ /(1-τ₁) can be interpreted as an index of global progressivity. We estimate the regressions of the two characteristics of the optimal TTRs against the five “primitives”.¹³ The results are shown in Table 1 and commented Section 5.

Table 1

“Current” and optimal TTRs

		Current*	k = .00	k = .05	k= .075	k = .10	k =.125	k = .15
France	τ₀	603.27	61.43	181.72	265.57	367.97	453.77	592.02
	τ₁	0.52	0.93	0.88	0.84	0.80	0.76	0.70
	τ₂	3.01×10^-6	-0.0000×10^-6	0.0106×10^-6	0.013×10^-6	0.011×10^-6	0.0098×10^-6	0.0097×10^-6
	τ₃	-1.51×10^-11	0.0004×10^-11	0.0062×10^-11	0.015×10^-11	0.005×10^-11	0.0064×10^-11	0.0053×10^-11
	τ₄	0.20×10^-16	0.0009×10^-16	0.008×10^-16	0.014×10^-16	0.017×10^-16	0.0098×10^-16	0.0051×10^-16
Germany	τ₀	427.9	427.9	454.23	554.48	600.91	600.9075	701.7375
	τ₁	0.71	0.71	0.69	0.66	0.64	0.64	0.61
	τ₂	0.0016×10^-6	0.003×10^-6	0.001×10^-6	0.0001×10^-6	0.001×10^-6	0.002×10^-6	0.002×10^-6
	τ₃	0.0009×10^-11	0.005×10^-11	-0.002×10^-11	0.001×10^-11	0.001×10^-11	0.001×10^-11	0.001×10^-11
	τ₄	0.0022×10^-16	0.010×10^-16	0.004×10^-16	0.001×10^-16	0.001×10^-16	0.004×10^-16	0.002×10^-16
Italy	τ₀	217.24	98.99	177.28	236.69	270.67	350.15	417.72
	τ₁	0.745	0.752	0.698	0.66	0.63	0.58	0.53
	τ₂	-1.98×10^-6	-0.02×10^-6	-0.01×10^-6	0.002×10^-6	0.005×10^-6	0.0002×10^-6	0.0008×10^-6
	τ₃	0.69×10^-11	0.04×10^-11	0.01×10^-11	0.004×10^-11	0.004×10^-11	0.0000×10^-11	-0.0004×10^-11
	τ₄	-0.07×10^-16	-0.02×10^-16	-0.01×10^-16	-0.0000×10^-16	0.003×10^-16	0.0005×10^-16	0.0025×10^-16
Luxembourg	τ₀	1469.68	615.73	680.78	746.64	809.23	858.74	926.17
	τ₁	0.316	0.761	0.75	0.717	0.706	0.692	0.676
	τ₂	4.12×10^-6	0.228×10^-6	0.24×10^-6	0.23×10^-6	0.245×10^-6	0.227×10^-6	0.223×10^-6
	τ₃	-1.869×10^-11	0.019×10^-11	0.022×10^-11	0.014×10^-11	0.051×10^-11	0.041×10^-11	0.013×10^-11
	τ₄	0.25×10^-16	0.07×10^-16	0.017×10^-16	0.075×10^-16	0.008×10^-16	0.009×10^-16	-0.004×10^-16
Spain	τ₀	196.42	227.43	225.51	436.88	481.18	493.54	498.23
	τ₁	0.97	0.81	0.81	0.65	0.61	0.60	0.60
	τ₂	-4.24×10^-6	0.001×10^-6	0.0005×10^-6	-0.0012×10^-6	0.001×10^-6	0.0005×10^-6	-0.0001×10^-6
	τ₃	2.05×10^-11	0.001×10^-11	.0008×10^-11	-.0008×10^-11	0.0003×10^-11	-.0001×10^-11	0.0000×10^-11
	τ₄	-0.36×10^-16	0.001×10^-16	0.0008×10^-16	-0.003×10^-16	0.001×10^-16	0.0002×10^-16	0.0000×10^-16
United Kingdom	τ₀	455.51	289.08	564.61	564.82	628.61	749.57	864.62
	τ₁	0.66	0.80	0.61	0.61	0.57	0.48	0.40
	τ₂	1.717×10^-6	-0.0002×10^-6	0.0003×10^-6	0.0003×10^-6	0.001×10^-6	-0.005×10^-6	-0.001×10^-6
	τ₃	-2.008×10^-11	0.0002×10^-11	0.0001×10^-11	0.001×10^-11	-0.0006×10^-11	0.002×10^-11	-0.002×10^-11
	τ₄	0.505×10^-16	0.0001×10^-16	0.0001×10^-16	0.0004×10^-16	-0.0004×10^-16	-0.003×10^-16	-0.001×10^-16

*

In the “Current” column, the parameter τ are those of the polynomial approximation to the current TTR.

4.6. Computational vs analytical approach: a summary

After the detailed description of our computational approach in Section 4.1 – 4.5, it is useful to summarize the differences between the analytical approach and the computational approach that we propose in this paper.

Type of solution

The analytical approach provides an intensional solution to the optimal taxation problem,¹⁴ i.e. a rule according to which a specific optimal TTR can be computed for a specific economy (i.e. an extensional solution), by imputing economy-specific values to the parameters that defines the rule (the so-called “primitives”). For example, if the rule contains the (typically only one) wage elasticity of labour supply, the empirical application requires to impute a value to the elasticity. In the earliest empirical exercises (e.g. Mirrlees, 1971; Tuomala, 1990) the values imputed to the primitives, were reasonable assumptions or educated guesses or estimates derived from previous studies. More recent empirical exercises, mostly adopting the “sufficient statistics” version of the analytical approach, use estimates previously obtained with econometric models and/or calibration procedures (e.g. Saez, 2002; Immervoll et al. (2007); Brewer et al., 2008). The problem with imputing values produced by previous contribution is that those values might have been produced under assumptions that are very different from those that sustain the optimal taxation rule, thus introducing potential inconsistencies. The computational approach illustrated in this paper provides an extensional solution to the optimal taxation problem, i.e. it identifies a specific solution for a specific economy, whose “primitives” are embedded in the microeconometric model that simulates the households’ choices. This way, the solution that we get for a specific economy is by construction consistent with the assumptions which the microeconometric model rests upon. As explained in section 4.5, a general (i.e. intensional) solution can then be approximated by identifying the mapping from the “primitives” of a sample of economies to the specific (extensional) solutions obtained for the various economies.

Assumptions on households’ behaviour and economic environment

The first generation of analytical optimal taxation (e.g. Mirrlees, 1971) assumes individual with identical preferences and different productivity, who choose an interior solution given an opportunity set only defined by exogenous wage rate, exogenous income and tax rule. Most of the empirical exercises assume quasi-linear preferences and constant elasticity. The more recent “sufficient statistics” approach (e.g. Saez, 2001; Saez, 2002) in principle is able to allow more easily for different types of households, corner solutions and heterogeneity of preferences. However, as observed in Section 2, it only provides implicit solutions that in general are not sufficient to identify a global optimal TTR. For this purpose the implicit solutions must be complemented by ad-hoc assumptions or explicit structural hypothesis. In the computational approach, the assumptions are those of the microeconometric model. They can be very flexible as regards to the household preferences and the structure of the economic environment, for example they can account for quantity constraint and complicated opportunity sets.

Definition of the optimal TTR

The analytical approach provides a non-parametric TTR: a formula that allows to compute the optimal marginal tax rate corresponding to any given level of productivity or of taxable income. In principle, this might be possible also with a computational approach. However, the approach adopted in this paper identifies the optimal TTR within a parametric class (the Ramsey approach). Clearly the latter approach is less general than the non-parametric one. Yet the greater generality of the non-parametric TTR implies more restrictive assumptions on households’ preferences and opportunity sets. Moreover, it’s worthwhile noting that the optimal non-parametric TTRs appear to be easily approximated by parametric expressions.

5. Results

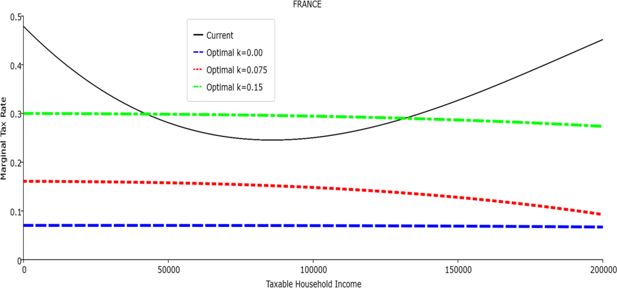
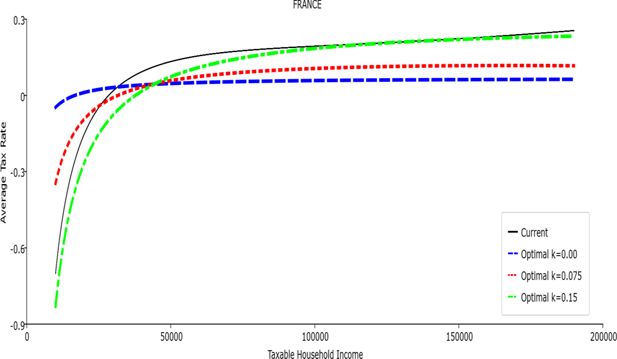
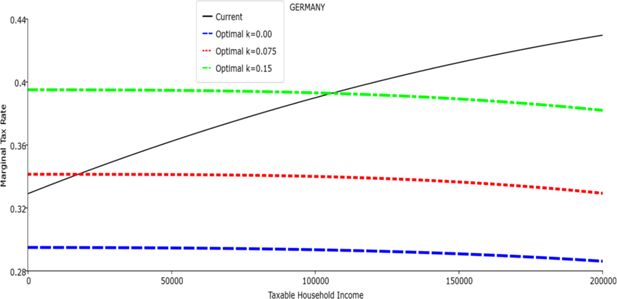
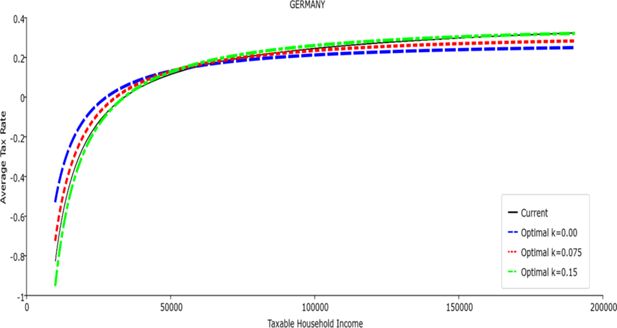
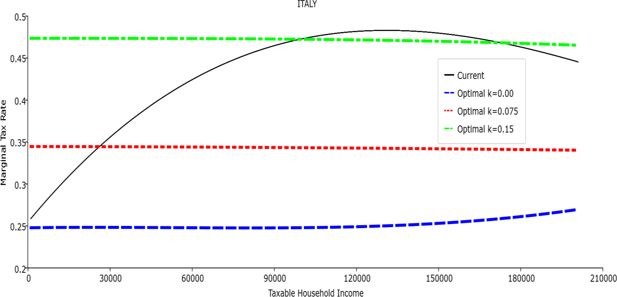
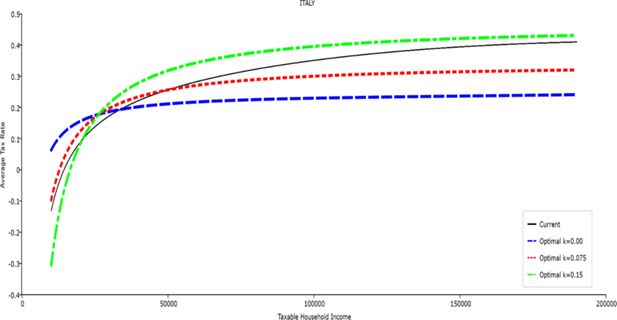
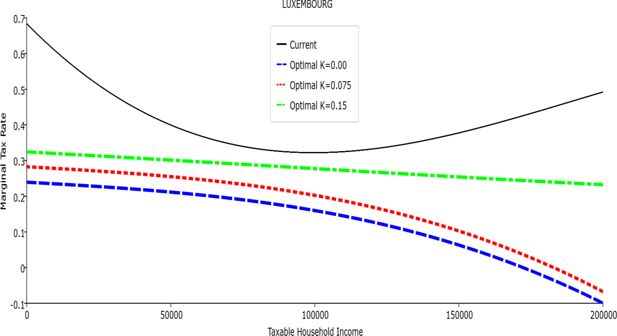
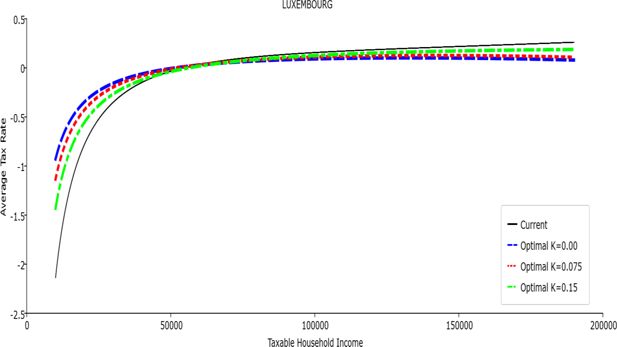
Table 1 reports the parameters of the polynomial optimal TTRs and the polynomial approximation to the current TTRs. The polynomial approximations to the current TTR are just shown to provide a simple comparison between the optimal rules and the current ones: all the other results (welfare and economic effects) relative to the current TTRs are actually obtained with the real current TTRs, not the approximated ones. The welfare gains of the optimal TTRs and the “winners” with respect to the current TTR are reported in Table 2. Figures 1–12 show the marginal tax rates (MRTs) and the average tax rates (ATRs) of the optimal polynomial TTRs and of the approximated current TTRs. Figures 13–20 illustrate other aspects of the welfare and economic effects of the optimal rules.

Figure 1

Download asset Open asset

Marginal Tax Rate vs. Taxable Income. France

Figure 2

Download asset Open asset

Average Tax Rate vs. Taxable Income. France

Figure 3

Download asset Open asset

Marginal Tax Rate vs. Taxable Income. Germany

Figure 4

Download asset Open asset

Average Tax Rate vs. Taxable Income. Germany

Figure 5

Download asset Open asset

Marginal Tax Rate vs. Taxable Income. Italy

Figure 6

Download asset Open asset

Average Tax Rate vs. Taxable Income. Italy

Figure 7

Download asset Open asset

Marginal Tax Rate vs. Taxable Income. Luxembourg

Figure 8

Download asset Open asset

Average Tax Rate vs. Taxable Income. Luxembourg

Figure 9

Download asset Open asset

Marginal Tax Rate vs. Taxable Income. Spain

Figure 10

Download asset Open asset

Average Tax Rate vs. Taxable Income. Spain

Figure 11

Download asset Open asset

Marginal Tax Rate vs. Taxable Income. United Kingdom

Figure 12

Download asset Open asset

Average Tax Rate vs. Taxable Income. United Kingdom

Figure 13

Download asset Open asset

France: %change of CMU by demographic group and decile, k = 0.075.

Figure 14

Download asset Open asset

Figure 15

Download asset Open asset

Italy: %change of CMU by demographic group and decile, k = 0.075.

Figure 16

Download asset Open asset

Luxembourg: %change of CMU by demographic group and decile, k = 0.075.

Figure 17

Download asset Open asset

Spain: %change of CMU b.y demographic group and decile, k =0.075

Figure 18

Download asset Open asset

The UK: %change of CMU by demographic group and decile, k = 0.075.

Figure 19

Download asset Open asset

%change of disposable income w.r.t. current values by country and Kolm’s k.

Figure 20

Download asset Open asset

Povery Gap Index by country and Optimal TTR (indexed by Kolm’s k).

Table 2

Welfare Gains and Welfare Winners

		k = .00	k = .05	k= .075	k = .10	k =.125	k = .15
France	Social Welfare Gain	159.23	89.63	53.17	16.37	-8.6	-45.47
	Equality Gain	0	-20.31	-20.64	-12.4	-1.86	20.3
	Efficiency Gain	159.23	109.94	73.81	28.77	-6.64	-65.77
	%Winners: All	67	67	66	65	64	61
	%Winners: Couples	66	66	65	64	62	57
	%Winners: Single Males	84	80	76	71	66	62
	%Winners: Single Females	51	55	57	61	66	72
Germany	Social Welfare Gain	-7.48	-5.00	41.05	71.39	87.65	155.27
	Equality Gain	0	-2.02	8.51	23.68	39.94	78.61
	Efficiency Gain	-7.48	-2.98	32.54	47.71	47.71	76.66
	%Winners: All	46	44	46	46	46	49
	%Winners: Couples	41	41	41	41	41	41
	%Winners: Single M	37	38	38	40	40	41
	%Winners: Single F	55	56	62	63	63	71
Italy	Social Welfare Gain	72.9	45.93	28.4	18.64	-1.35	-18.54
	Equality Gain	0	-3	-3.06	-2.97	0.13	3.16
	Efficiency Gain	72.9	48.93	31.46	21.61	-1.48	-21.70
	%Winners	56	58	58	57	53	52
	%Winners: Couples	51	49	44	42	38	36
	%Winners: Single M	59	66	69	70	63	61
	%Winners: Single F	58	63	65	65	64	63
Luxembourg	Social Welfare Gain	2.06	-35.63	-68.35	-62.63	-67.54	-66.94
	Equality Gain	0	-41.82	-43.04	-46.45	-40.26	-27.94
	Efficiency Gain	2.06	6.19	-25.31	-16.18	-27.28	-39.00
	%Winners	45	48	46	48	49	51
	%Winners: Couples	54	59	54	58	59	61
	%Winners: Single M	31	32	31	30	30	30
	%Winners: Single F	44	47	48	50	52	56
Spain	Social Welfare Gain	-16.99	-13.87	10.65	13.83	21.35	27.17
	Equality Gain	0	2.17	13.88	20.25	25.47	30.29
	Efficiency Gain	-16.99	-16.04	-3.23	-6.42	-4.12	-3.12
	%Winners	73	73	67	63	63	63
	%Winners: Couples	75	75	63	56	56	55
	%Winners: Single M	70	70	72	70	70	70
	%Winners: Single F	70	70	73	73	74	74
United Kingdom	Social Welfare Gain	-18.37	37.42	37.81	48.34	65.19	77.19
	Equality Gain	0	0.81	1.14	1.24	0.64	-0.17
	Efficiency Gain	-18.37	36.61	36.67	47.10	64.55	77.36
	%Winners: All	42	76	77	79	81	82
	%Winners: Couples	23	79	82	84	88	90
	%Winners: Single M	57	64	64	65	66	68
	%Winners: Single F	64	82	83	83	83	82

The optimal TTRs

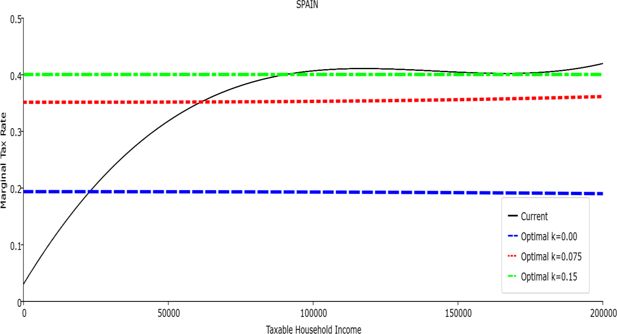
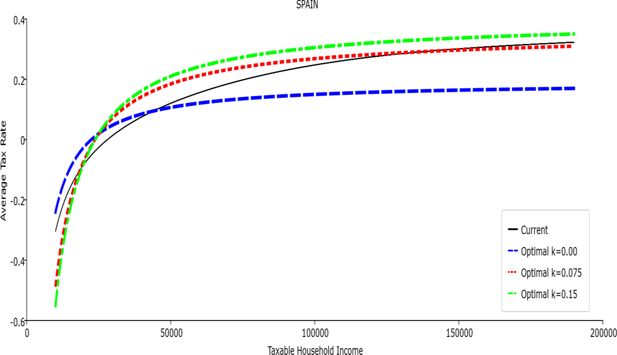
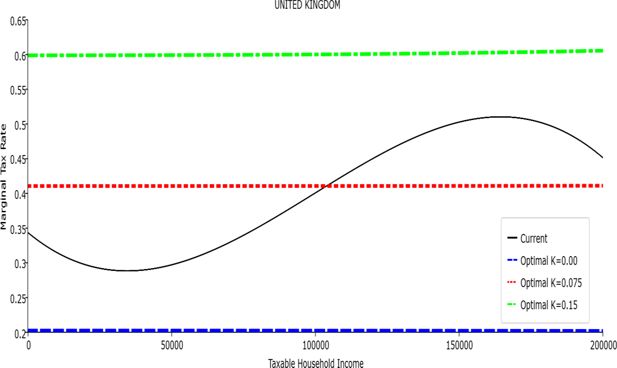
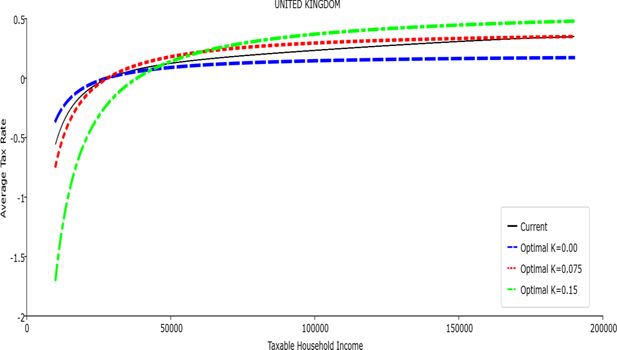
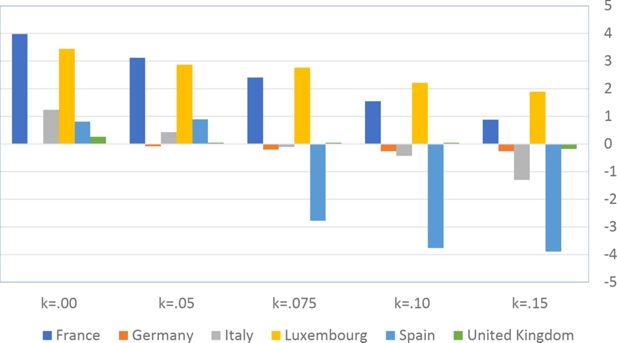
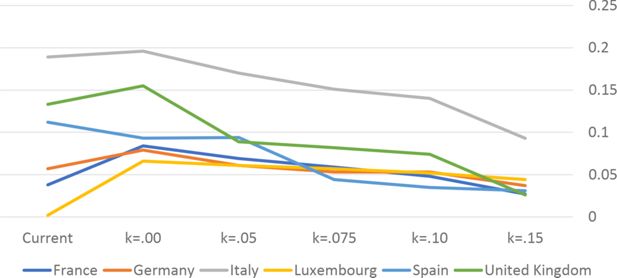
In all the countries, $\tau _{0}$ is always positive and the shape of the optimal TTRs is dominated by τ₁, while the other parameters are very small and might exert some influence only at large taxable incomes (e.g. above 150000 euro a year). As a consequence, the optimal TTRs are very close to a FT equal to 1-τ₁ plus a UBI (or equivalently a NIT). In contrast, in all the countries, the polynomial approximation to the current TTR features important non-linearities. Parameter $\tau _{0}$ is the monthly universal basic income (or guaranteed minimum income according to the NIT interpretation) for a one-person household. For a N-person household it must be multiplied by N^1/2. Notice that the value $\tau _{0}$ of the approximated current TTR is not strictly comparable to the optimized value of $\tau _{0}$ , since the latter is a universal and unconditional transfer to be received with certainty, while the former is an expected value across the population of various - mostly means-tested, contingent and categorical - transfers. It makes sense, however, to interpret $\overset{\hat }{\tau }_{0}$ as a measure of the expected current expenditure in income support policies from the view-point of the public budget constraint. In this perspective – without implying direct policy prescriptions – the current policies appear to be more or less cost-effective than those indicated by the optimized rules. In France and Luxembourg, the current income support policies appear to be “too costly”: a less expensive UBI would attain a higher Social Welfare (for k < 0.125 in France and for k < 0.05 in Luxembourg). The opposite holds in Germany and Italy (for k > 0.05), Spain (for all considered value of k) and the United Kingdom (for k $\geq$ 0.05). The main features of the optimal polynomial TTRs are also illustrated in the Figures 1–12. The effects of the other parameters $\tau _{1},...,\tau _{4}$ on the shape of the TTRs are illustrated by the Figures 1–12, which respectively represent MTR and ATR as functions the household total taxable income.¹⁵ The graphs are built under the assumption that the optimal TTRs are implemented by paying the UBI and then applying the tax rates to the taxable income. Note the almost flat MTR hold whatever the value of the inequality aversion parameter k. The implication is that, within the TTR class considered, a certain degree of progressivity is more efficiently attained by a UBI or a NIT with non-distortive MTRs rather than by increasing and distortive MTRs. We also represent the MTR of the polynomial approximation to the current TTR. Note that it does not correspond to official values of the current MTRs. It measures the change – averaged across the households – in total household taxes when total household taxable income increases by one euro. It shows striking differences both between the countries and with respect to the optimal polynomial TTRs. The current systems in France and Luxembourg appear to envisage relatively generous income support policies at low or zero income followed by very high implicit marginal benefit reduction rates. The optimal rules suggest less expensive (although universal and unconditional) income support and a longer and smoother phase-out. Germany envisages an expensive current income support policies and yet a slowly increasing MTR on low incomes. In Italy and Spain, the current MTRs are first steeply increasing up to taxable incomes around 100,000 and then decreasing.

Given that the optimal MTRs are very close to a constant, the ATRs (Figures 1–12) are useful to show the level and type of progressivity implied by the various TTRs in the different countries.¹⁶ If the Social Welfare criterion ignores inequality effects (i.e. k = 0.00), in all the countries the optimal TTR – as compared to the current TTR – is more progressive on low levels of taxable income and less progressive on middle or high taxable incomes. The opposite happens with k=0.15. This holds in general, although in Luxembourg and Germany the ATRs are very close for different values of k, i.e. the ATR behaves approximately in the same way whatever the value of k. For k = 0.075, the optimal ATR is closer to the current one, but less progressive on middle and high incomes in France and Italy.

Welfare effects

The Social Welfare Gains, the Equality Gains and the Efficiency Gains due to the optimal polynomial TTRs (with respect to the current TTFs) by country and Kolm’s k are reported in Table 2. For most countries and most values of k, the optimal polynomial TTR is social welfare superior to the current TTR. This result holds in France and Italy for k < 0.15, in Luxembourg for k < 0.05, in Germany and Spain for k $\geq$ 0.075 and in the United Kingdom for k $\geq$ 0.05. What happens is that the polynomial optimal TTRs are mainly disequalizing in France, Italy and Luxembourg but equalizing (for a majority of k values) in Spain and in the United Kingdom. As consequence, higher values of k – i.e. higher costs of inequality – tend to overcome the efficiency effect in the former group of countries and strengthen it in the latter one. These results are also due to the efficiency gain, which decreases with k in the first group of countries while it increases in the second one.

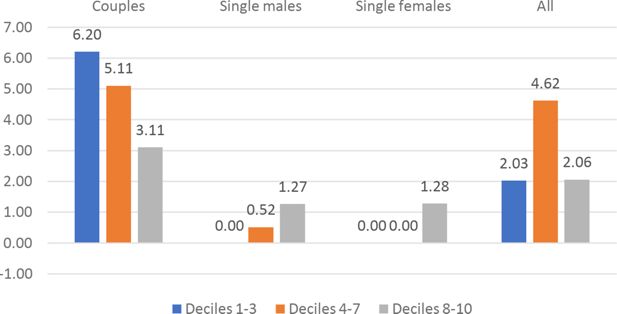
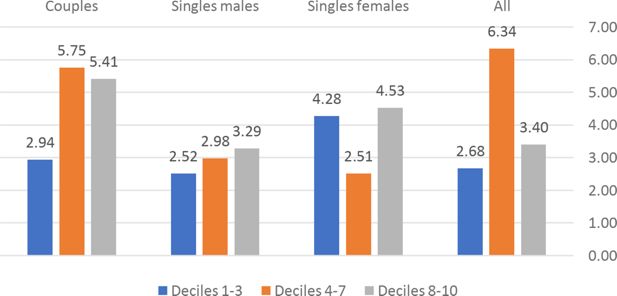
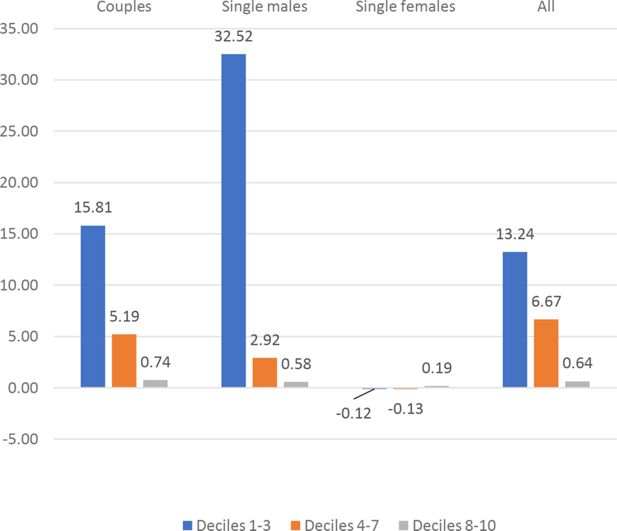
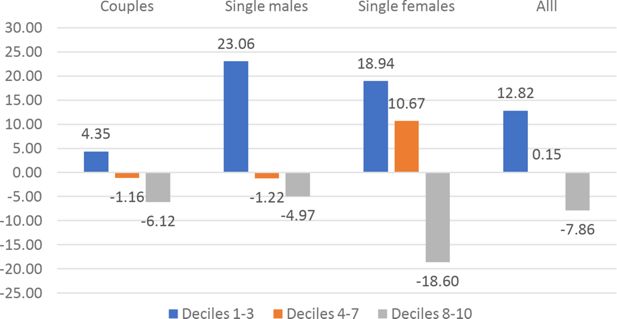
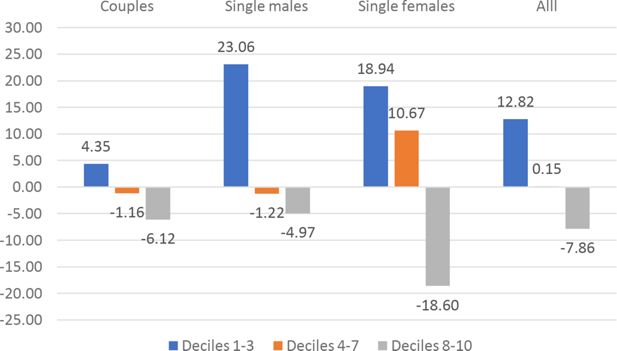
Besides the overall Social Welfare effects, we can identify specific welfare effects for different demographic groups. We have computed the CMU (Section 4.3) of couples, single males and single females under the current TTR and under the optimal TTRs for k = .075.¹⁷ show the average CMU gains for the different demographic groups, by decile (1-3, 4-7, 8-10) of current CMU distribution. The graphs show an extreme heterogeneity across countries, demographic groups and deciles. Depending on the country, some groups and/or some deciles are penalized by the optimal polynomial TTRs. System like UBI+FT or NIT+FT are typically expected to penalize middle income deciles. In our results this seems to be the case except for France and Germany.¹⁸

Table 2 shows also the percentages of households who “win” under the optimal polynomial TTRs by country, type of household (couple, single male, single female) and Kolm’s k. A household is classified as a winner if its CMU under the optimal polynomial TTR is larger than its CMU under the current TTR. The information conveyed is ordinal and therefore is different from the cardinal information conveyed by. The percentage of winners can be interpreted as an estimate of the support that a given TTR would receive in a referendum. Also the results on winners confirm the heterogeneity of the effects of the optimal TTRs, which receive more support by single females in Germany, by single female and single males in Italy and by couples in Luxembourg. By contrast, in France, Spain and the U.K., the optimal TTRs receive a rather uniform support by the different type of households.

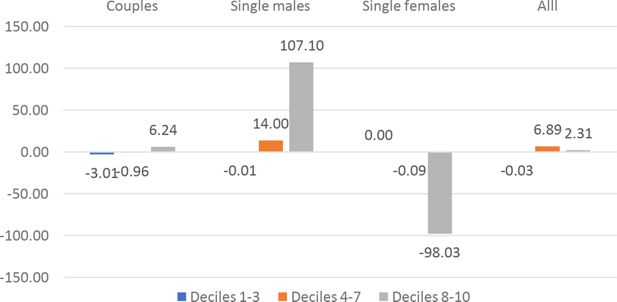
Economic effects

Figure 19 and Figure 20 represent the percentage change in disposable income and the Poverty Gap Index respectively, by country and Kolm’s k. The two graphs illustrate a dimension of the efficiency-equality trade-off. Disposable income increases as long as $k\leq 0.05$ , with the exception of Germany. With k > 0.05 it keeps increasing in France and Luxembourg, while it decreases in Germany, Italy and the United Kingdom. The aggregate effects on labour supply (not reported) are small and consistent with the dynamics of disposable income. The Poverty Gap Index increases when the economy adopt the polynomial optimal TTR with k = 0, then it decreases with increasing inequality aversion k.

The “primitives” and the optimal TTRs

Table 3 shows illustrative results obtained by inferring a general rule that links the “primitives” to the optimal TTRs, i.e. it presents the results of the analysis explained in Section 4.5. We have well-defined results on UBI (τ₀): all the coefficients are significant at standard levels . Kolm’s k, Productivity and Elasticity (both extensive and intensive) elasticities favour a higher UBI. A stricter Budget require a lower UBI. Among the above results, the surprising one is the effect of elasticities. A possible explanation is that UBI, as compared to means-tested policies does not suffer from poverty-traps, therefore its relative advantage is greater the more elastic is household behaviour. Kolm’s k and Extensive elasticity respectively favour a lower and a higher Leading Tax rate: the former result, taken together with k’s effect on UBI, seems to mean that more egalitarian social preferences favour a higher UBI rather than higher taxes; the latter result might mean that less distortions are better achieved with UBI than with lower taxes. Let us imagine we want to propose a common TTR to all the countries, based on the averages of the “primitives”. Let us also suppose that social preferences are such that k = 0.075. Then the UBI (or equivalently the guaranteed minimum income in a NIT rule) and the leading tax rate of the common polynomial optimal TTR would be 456 monthly euros (for one-person household) and 29.8% respectively. It is close to the optimal TTR in Germany for k = 0.05.

Table 3

“Primitives” of the economy and characteristics of the optimal polynomial TTRs

	UBI	Leading Tax Rate
Constant	357.28 2.14	-5.04 -0.3
Kolm’s k	25.44 14.01	1.40 9.95
Productivity	0.22 11.29	0.002 1.48
Extensive Elasticity	117.35 3.05	9.90 3.31
Intensive Elasticity	253.55 8.44	1.46 0.62
Budget	-0.25 -8.08	0.002 -0.85
R²	0.83	0.88
Standard error of the estimate	53.69	0.04

t-values in italics below the estimates.
Bold estimates are significant at standard levels.

Concluding remarks

Two main approaches to empirical optimal income taxation have been used so far in the literature: the analytical and the computational approach.

In this paper we develop a version of the computational approach that combines microeconometric modelling, microsimulation, numerical optimization and social welfare evaluation in a consistent way.

We consider the class of 4th degree polynomial TTRs, i.e. a generic rule that represents total household disposable income as a 4th degree polynomial function plus a constant. We adopt the Kolm’s social welfare function. A specific TTR is defined by the parameter vector containing the four coefficients of the polynomial and the constant. We identify optimal TTRs for different degrees of social inequality aversion and compare them to the current rules in six European countries.

For most countries and most values of the inequality aversion parameter, the optimal polynomial rules provide a higher social welfare than the current ones. The class of TTRs considered as candidates for welfare optimality, although flexible, is extremely simple. It is applied to the total taxable household income, irrespective of the source of income. It does not depend on household’s socio-economic characteristics, with the exception that the number of household members that affects the basic income transfer. It is of course quite possible that we might do better by taking households’ heterogeneity into account when designing the optimal TTR. However, finely categorized, targeted and means-tested TTRs bear administration and political costs (complex forms to file out, monitoring, political manipulation, lack of transparency, conflict resolution etc.) that are certainly less important or even not existent in simple and universalistic TTRs.

The results suggest some common features in all the countries. The optimal polynomial TTRs are very close to a (almost) FT plus UBI or equivalently plus NIT. The profiles of the MTRs are pretty similar in different countries and definitely flatter than under the current TTRs. This results hold for all the countries and all the values of the inequality aversion k, despite the fact that the polynomial TTR class is flexible and the heterogeneous responses allowed by the microeconometric model might induce very different shapes of the optimal TTRs. These results confirm those of Islam and Colombino (2018). This is remarkable, since Islam and Colombino (2018) only compare the NIT+FT rule to the current TTR, while the polynomial class considered in this paper is very flexible and compatible with many different shapes of the TTR. The social welfare gains due to the optimal polynomial TTRs are admittedly small. However, the results show that extremely simple universalistic TTRs (five parameters) can at least match the performance of the very complex current TTRs (dozens or even hundreds of parameters).

The TTRs that come out as optimal in our exercise are far from the current ones. However, they are not outside the choice set considered by the policy debate. The FT has been implemented in many Eastern European countries and it has been proposed by many economists.¹⁹ UBI is receiving an increasing interest.²⁰ The “package” UBI+FT has been studied with a micro-macro model by Magnani and Piccoli (2020). A recent theoretical and empirical (stochastic dynamic macroeconomic model) analysis by Ferriere et al. (2021) gives support to the conclusion that a TTR close to UBI+FT might be optimal.

Despite the above common features, we can see large differences between the levels of UBI and the values of the MTRs under the optimal polynomial TTRs in the different countries. They depend indeed on various characteristics of the population and the economic environment.

The differences of optimal TTRs in different countries, therefore, call for a further step. An explanation of these differences among countries requires to identify a general relationship between the basic (“primitive”) characteristics of the economy and the features of the optimal TTRs. Actually, this is the direct result of the analytical solution of optimal taxation. We can come close to a similar result by replacing the analytical solution with microsimulation and numerical optimization. Even with a limited number of countries, we exemplify the procedure that can be used to identify the effects of “primitives” (Kolm’s k, Productivity, Extensive and Intensive Elasticities, Public budget constraint) upon two characteristics of the optimal TTRs (UBI and Leading tax rate). A notable and surprising results is that elasticity favours a preference for UBI while it has a little effect on taxes. Also, more egalitarian social preferences favour a higher UBI rather than higher taxes. Overall, it seems that that less distortions and more equality are better achieved through UBI rather than through taxes.

As a final comment, it must be noted that the level of abstraction of the computational exercise illustrated in this paper is close to the one that characterizes the analytical approach. A similar level of abstraction holds by construction for any exercise in empirical optimal taxation, but in the case of our exercise is also due to an explicit choice (i.e. choosing a simple – though flexible – and universalistic class of TTRs). Moreover, we claim that the computational approach might have better opportunities to reflect realistic features of the economy (due to the use of a flexible microeconometric model). Although the results of optimal taxation exercises cannot be taken as immediate recipes for reform, yet they indicate reform directions that might deserve further detailed investigations, which can then account – to a certain extent – for some of the features and constraints that presumably led the current real TTR. The challenge being to identify policy flaws that can be fixed by reforms.²¹

Footnotes

1.

It is interesting to see that the modern dynamic general equilibrium literature (e.g. Ferriere et al., 2021; Heathcote and Tsujiyama, 2021) appears to prefer the “Ramsey approach” (parametric tax rule) rather than the “Mirlees approach” (non-parametric tax rule).

2.

See for example: Atkinson (1996), Colombino (2015), Colombino and Islam (2018), Colombino and Narazani (2013), Gentilini et al. (2020), Ghatak and Jaravel (2020), Ghatak and Maniquet (2019), Grimalda et al. (2020), Islam and Colombino (2018), Magnani and Piccoli (2020), Moene and Ray (2016), Standing (2011; 2015), Van Parijs and Vanderborght (2017).

3.

Of course one might adopt different evaluation criteria, such as the effects on employment, poverty etc. We adopt a social welfare criterion but we will also report and discuss results on other indices that might be policy-relevant.

4.

Given the limited number of countries, we are only able to present an illustrative example of the identification of the “mapping” from “primitives” to optimal TTrs.

5.

The acronym RURO (= Random Utility-Random Opportunity) is proposed by Aaberge and Colombino (2014).

6.

The dataset for France is the Statistics on Resources and Living Conditions (SRCV) survey, the France part of the EU-SILC survey produced by Public Statistics Data Archives (ADISP).

7.

EUROMOD is a large-scale pan-European tax-benefit static micro-simulation engine (e.g. Sutherland and Figari, 2012). It covers the tax-benefit schemes of the majority of European countries and allows computation of predicted household disposable income, on the basis of gross earnings, employment and other household characteristics.

8.

In all the optimal TTRs we obtain τ₀ > 0. The equivalence of a universal basic income and a universal negative income tax with guaranteed minimum income can be easily seen in the flat tax case, although it carries over to non-flat taxes. See for example Hoynes and Rothstein (2019).

9.

In this paper we identify optimal TTRs for six value of k: 0.0, 0.05, 0.075, 0.10, 0.125, and 0.15. It can be shown (Islam and Colombino, 2018) that the corresponding values of the popular Atkinson’s parameter of inequality aversion are approximately 0.000, 0.114, 0.180, 0.252, 0.333 and 0.424.

10.

Kolm’s Inequality Index is an absolute index, meaning that it is invariant with respect to translations (i.e. adding a constant to every μ_i). Absolute indices are less popular than relative indices (e.g. Gini’s or Atkinson’s), although there is no strict logical or economic motivation for preferring one to the other. Atkinson and Brandolini (2010) provide a discussion of relative indices, absolute indices and intermediate cases. Depending on the specific applcation, there might be a motivation of computational convenience for choosing one or another type of index. Blundell and Shephard (2012) adopt a social welfare index which turns out to be very close to Kolm’s index. Their main motivation for their index seems to be computational, since it handles negative numbers (random utility levels). Our motivation is analogous.

11.

In order to locate a global maximum, we partition the parameter space and try different starting values.

12.

It might be argued that “primitives” 2 – 5, are not really primitives, since they are also determined by the current TTRs. This is true, but it is not really relevant. We interpret our analysis as conditional upon the current economy.

13.

With a suitable – larger – sample of countries, one could adopt a better method. For example, the identification of the optimal TTR in a country could be modelled as a conditional logit, where the decision maker is the “social planner”, the objects of choice are alternative TTRs belonging to the polynomial class and the “primitives” interact with the attributes of the alternative TTRs. Then one could estimate the effects of the “primitives” upon the attributes of the chosen TTR.

14.

The term intensional (as the term extensional at point b) is used in the logical sense. For example, the intensional definition of an object is a specification of the characteristics that permit to identify the object. The extensional definition of an object consists of directly pointing at (or showing) the object.

15.

In Graphs 1 – 12 the current MTRs and ATRs are computed with the polynomial approximation to the true current TTR (see the end of Section 4.2).

16.

A simple index of progressivity is MTR/ATR.

17.

The shape of results is similar for different values of k.

18.

These problems might probably be moderated by a country-specific design of the equivalence scale applied to the basic income.

19.

e.g. Hayek (1956), Friedman (1962), Hall and Rabushka (1995), Heath (2006).

20.

Among many others: Colombino (2019), Hoynes and Rothstein (2019), Ghatak and Maniquet (2019), Benzell and Ye (2021).

21.

The Mirrlees Review represents a notable example where abstract optimal taxation results – in that case obtained by the Mirrlees-Saez methods – are taken as a basis for formulating specific reform proposal (Mirrlees et al., 2011).

Appendix 1

Table A1

Maximum likelihood estimates – couples (France)

Model component	Variable	Coef.	Std. Err.
Opportunity density		δ
	Employee_Man	0.4761696	0.3665576
	Self-employed_Man	0.2130577	0.3805561
	Employee_Woman	-0.3649212	0.2853927
	Self-employed_Woman	-1.426779	0.3241603
	Part-time_Employee_Man	-0.3805255	0.2414433
	Full-time_Employee_Man	2.83453	0.1249029
	Part-time_Self-employed_Man	-1.841048	0.324269
	Full-time_Self-employed_Man	0.2870089	0.1540075
	Part-time_Employee_Woman	0.6361778	0.2170085
	Full-time_Employee_Woman	2.698627	0.1676399
	Part-time_Self-employed_Woman	-1.014395	0.3149686
	Full-time_Self-employed_Woman	0.6781008	0.2277644
Income		γ
	Household_Disposable_income	0.0003342	0.0001334
	Hosuhold_Disposable_income squared	1.61E-08	6.75E-09
	Household_size X Household_disposable_income	-0.0000513	0.0000175
Leisure		λ
	Leisure_Male	0.1256514	0.0281893
	Leisure_Man squared	0.0000173	0.0001373
	Leisure_Woman	0.163189	0.0255661
	Leisure_Woman squared	-0.000107	0.0001529
	Leisure_Man X Household_disp_income	-7.88E-06	1.02E-06
	Leisure_Woman X Household_disp_income	-1.54E-07	8.04E-07
	Leisure_Man X Age_Man	-0.0059183	0.0011829
	Leisure_Woman X Age_Woman	-0.0085386	0.0009848
	Leisure_Man X Age_Man squared	0.0000742	0.0000138
	Leisure_Woman X Age_Woman squared	0.0001108	0.000012
	Leisure_Man X No. Children	-0.0026133	0.0017907
	Leisure_Woman X No. Children	0.0084813	0.0015617
	Leisure_Man X No. Children0-6	0.0027957	0.0025747
	Leisure_Man X No. Children7-10	0.006507	0.0027523
	Leisure_Woman X No. Children0-6	0.006981	0.0021144
	Leisure_Woman X No. Children7-10	0.0007436	0.002288
	Leisure_Woman X Leisure_Man	0.0001134	0.0000948

	N.observations (N. couples*49 alternatives)	195804
	N.couples	3996
	LR chi2(32)	15140.15
	Prob > chi2	0
	Pseudo R2	0.4868
	Log likelihood	-7981.6412

Table A2

Maximum likelihood estimates – singles (France)

		Male		Female
Model component	Variable	Coef.	Std. Err.	Coef.	Std. Err.
Opportunity density		δ		δ
	Employee	0.199478	0.533068	-1.19744	0.470041
	Self_employed	-0.21333	0.593638	-1.68397	0.553979
	Part-time_Employee	-0.69588	0.393698	1.256628	0.352174
	Full-time_Employee	2.213382	0.253926	2.994315	0.267448
	Part-time_Self-employed	-2.70132	0.585303	-1.80785	0.627849
	Full-time_Self-employed	-0.28412	0.336337	0.368914	0.377033
Income		λ		λ
	Disposable income	-0.00012	0.00024	7.55E-05	0.000379
	Disposable income squared	4.53E-08	2.07E-08	6.64E-08	4.13E-08
	Household size X Disp_income	-5.6E-05	4.62E-05	-6.7E-05	6.84E-05
Leisure		λ		λ
	Leisure	0.129227	0.029882	0.15447	0.034747
	Leisure2	-8.1E-05	0.000239	-9.2E-05	0.000254
	Leisure X Disposable income	1.01E-06	2.34E-06	6.43E-07	3.40E-06
	Leisure X Age	-0.00516	0.000963	-0.0075	0.001086
	Leisure X Age squared	6.36E-05	1.21E-05	0.000092	1.34E-05
	Leisure X No. Children	-0.01374	0.005121	0.006768	0.003433
	Leisure X No. Children 0-6	-0.00814	0.019875	0.015925	0.00544
	Leisure X No. Children 7-10	0.011728	0.010413	0.008727	0.004892
Other
	N.observations (N. single*7 alternatives)	9331		10465
	N.single	1333		1495
	LR chi2(17)	2318.15		2657.35
	Prob > chi2	0		0
	Pseudo R2	0.4468		0.4567
	Log likelihood	-1434.83		-1580.46

Table A3

Maximum likelihood estimates – couples (Germany)

Model component	Variable	Coef.	Std. Err.
Opportunity density		δ
	Employee_Man	-0.5269339	0.435726
	Self-employed_Man	-1.611115	0.4373339
	Employee_Woman	-1.560942	0.2543809
	Self-employed_Woman	-3.580387	0.3637122
	Part-time_Employee_Man	-0.9591195	0.2591677
	Full-time_Employee_Man	2.516702	0.1205793
	Part-time_Self-employed_Man	-1.797576	0.3673868
	Full-time_Self-employed_Man	0.940684	0.1597094
	Part-time_Employee_Woman	1.829915	0.2318468
	Full-time_Employee_Woman	2.531309	0.1913391
	Part-time_Self-employed_Woman	0.8422771	0.341443
	Full-time_Self-employed_Woman	1.067966	0.2761494
Income		γ
	Household_Disposable_income	0.001699	0.0001136
	Hosuhold_Disposable_income squared	-5.60E-08	5.58E-09
	Household_size X Household_disposable_income	0.0000479	0.0000222
Leisure		λ
	Leisure_Male	0.184064	0.0264439
	Leisure_Man squared	-0.0004684	0.0002088
	Leisure_Woman	0.2376265	0.0251642
	Leisure_Woman squared	-0.0011735	0.00014
	Leisure_Man X Household_disp_income	-1.38E-05	7.25E-07
	Leisure_Woman X Household_disp_income	-9.65E-06	5.79E-07
	Leisure_Man X Age_Man	-0.0030924	0.0009326
	Leisure_Woman X Age_Woman	-0.0046903	0.0009542
	Leisure_Man X Age_Man squared	0.0000357	0.0000106
	Leisure_Woman X Age_Woman squared	0.0000713	0.0000112
	Leisure_Man X No. Children	-0.0017621	0.0019208
	Leisure_Woman X No. Children	0.0231159	0.0016417
	Leisure_Man X No. Children0-6	0.0184762	0.0025177
	Leisure_Man X No. Children7-10	-0.0007047	0.0032015
	Leisure_Woman X No. Children0-6	0.01427	0.0025455
	Leisure_Woman X No. Children7-10	0.0037864	0.0026824
	Leisure_Woman X Leisure_Man	-0.0003689	0.0000744
Other
	N.observations (N. couples*49 alternatives)	201,243
	N.couples	4107
	LR chi2(32)	14394.76
	Prob > chi2	0
	Pseudo R2	0.4503
	Log likelihood	-8786.3249

Table A4

Maximum likelihood estimates – singles (Germany)

		Male		Female
Model component	Variable	Coef.	Std. Err.	Coef.	Std. Err.
Opportunity density		δ		δ
	Employee	-0.80193	0.57248	-1.43637	0.446197
	Self_employed	0.179376	0.597029	-8.15099	0.661612
	Part-time_Employee	-0.32109	0.406771	0.579569	0.34354
	Full-time_Employee	2.865958	0.240845	2.703306	0.249755
	Part-time_Self-employed	-2.54205	0.498362	4.688473	0.595456
	Full-time_Self-employed	0.184833	0.295293	4.011293	0.42799
Income		γ		γ
	Disposable income	0.003328	0.000448	0.003246	0.000196
	Disposable income squared	-7.89E-07	7.78E-08	-1.49E-07	1.28E-08
	Household size X Disp_income	6.42E-04	1.93E-04	8.93E-05	3.80E-05
Leisure		λ		λ
	Leisure	0.241596	0.03538	0.281701	0.033209
	Leisure2	-0.00076	0.000296	-0.00141	0.000258
	Leisure X Disposable income	-4.42E-05	2.40E-06	-3.86E-05	2.08E-06
	Leisure X Age	-0.00382	0.001035	-0.00337	0.001006
	Leisure X Age squared	5.09E-05	1.24E-05	4.29E-05	1.20E-05
	Leisure X No. Children	-0.02709	0.012505	0.014031	0.003459
	Leisure X No. Children 0-6	0.038387	0.020631	0.0287	0.007638
	Leisure X No. Children 7-10	0.016741	0.021338	0.017555	0.006452
Other
	N.observations (N. single*7 alternatives)	10,283		12,551
	N.single	1469		1793
	LR chi2(17)	2983.13		3608.3
	Prob > chi2	0		0
	Pseudo R2	0.5218		0.5171
	Log likelihood	-1366.98		-1684.87

Table A5

Maximum likelihood estimates – couples (Italy)

Model component	Variable	Coef.	Std. Err.
Opportunity density		δ
	Employee_Man	-2.227042	0.3359151
	Self-employed_Man	-1.793772	0.3327547
	Employee_Woman	-4.205803	0.3711781
	Self-employed_Woman	-3.159583	0.3091701
	Part-time_Employee_Man	1.810835	0.2235256
	Full-time_Employee_Man	3.457804	0.1466732
	Part-time_Self-employed_Man	-1.142189	0.2861769
	Full-time_Self-employed_Man	1.827801	0.1352579
	Part-time_Employee_Woman	3.522802	0.3488772
	Full-time_Employee_Woman	4.233018	0.3257372
	Part-time_Self-employed_Woman	0.2200945	0.3028192
	Full-time_Self-employed_Woman	1.989132	0.2580389
Income		γ
	Household_Disposable_income	0.0005129	0.0001534
	Hosuhold_Disposable_income squared	1.36E-08	7.25E-09
	Household_size X Household_disposable_income	-0.0001608	0.0000251
Leisure		λ
	Leisure_Male	0.0030689	0.05153
	Leisure_Man squared	-0.0000926	0.0001607
	Leisure_Woman	0.2598116	0.0365898
	Leisure_Woman squared	-0.000653	0.0001763
	Leisure_Man X Household_disp_income	4.38E-06	1.43E-06
	Leisure_Woman X Household_disp_income	-5.81E-07	1.01E-06
	Leisure_Man X Age_Man	-0.0015349	0.0025113
	Leisure_Woman X Age_Woman	-0.0097254	0.0016741
	Leisure_Man X Age_Man squared	0.0000135	0.0000318
	Leisure_Woman X Age_Woman squared	0.0001141	0.0000223
	Leisure_Man X No. Children	-0.0081218	0.0022336
	Leisure_Woman X No. Children	0.0078869	0.0017578
	Leisure_Man X No. Children0-6	0.0076125	0.0026554
	Leisure_Man X No. Children7-10	0.0002707	0.0028172
	Leisure_Woman X No. Children0-6	-0.0054445	0.0020634
	Leisure_Woman X No. Children7-10	-0.0009139	0.0020886
	Leisure_Woman X Leisure_Man	0.0003854	0.0000964
Other
	N.observations (N. couples*49 alternatives)	188405
	N.couples	3845
	LR chi2(32)	10209.91
	Prob > chi2	0
	Pseudo R2	0.3411
	Log likelihood	-9859.09

Table A6

Maximum likelihood estimates – singles (Italy)

		Male		Female
Model component	Variable	Coef.	Std. Err.	Coef.	Std. Err.
Opportunity density		δ		δ
	Employee	-1.22117	0.331639	-3.43019	0.3787
	Self_employed	-0.47643	0.315555	-2.81075	0.350903
	Part-time_Employee	1.263827	0.268794	3.554593	0.34008
	Full-time_Employee	3.310487	0.207522	4.654217	0.303264
	Part-time_Self-employed	-2.2652	0.32631	0.618142	0.341357
	Full-time_Self-employed	1.473456	0.180946	2.786139	0.266647
Income		γ		γ
	Disposable income	0.000114	0.000145	0.0003	0.000255
	Disposable income squared	5.12E-09	1.08E-08	6.55E-09	3.11E-08
	Household size X Disp_income	-5.5E-05	4.01E-05	-0.00011	4.77E-05
Leisure		λ		λ
	Leisure	0.280595	0.024332	0.312801	0.030346
	Leisure2	0.000164	0.000173	0.000428	0.000198
	Leisure X Disposable income	1.36E-06	1.55E-06	-1.91E-07	2.59E-06
	Leisure X Age	-0.01438	0.001037	-0.01841	0.001297
	Leisure X Age squared	0.000176	1.51E-05	0.000225	1.84E-05
	Leisure X No. Children	-0.0191	0.01175	0.005966	0.003381
	Leisure X No. Children 0-6	0.007813	0.020605	0.00305	0.005703
	Leisure X No. Children 7-10	0.011513	0.022161	-0.00433	0.005772
Other
	N.observations (N. single*7 alternatives)	22190		18270
	N.single	3170		2610
	LR chi2(17)	4055.02		3501.41
	Prob > chi2	0		0
	Pseudo R2	0.3287		0.3447
	Log likelihood	-4141.03		-3328.12

Table A7

Maximum likelihood estimates – couples (Luxembourg)

Model component	Variable	Coef.	Std. Err.
Opportunity density		δ
	Employee_Man	2.798179	1.230943
	Self-employed_Man	1.196799	1.218041
	Employee_Woman	-1.670879	0.4877308
	Self-employed_Woman	-3.273727	0.5811094
	Part-time_Employee_Man	-0.9321119	0.5778732
	Full-time_Employee_Man	2.740097	0.2477136
	Part-time_Self-employed_Man	-3.276221	1.176261
	Full-time_Self-employed_Man	0.3923308	0.4062014
	Part-time_Employee_Woman	2.251194	0.381928
	Full-time_Employee_Woman	3.024338	0.2864887
	Part-time_Self-employed_Woman	-0.0916981	0.6417357
	Full-time_Self-employed_Woman	0.9017009	0.4806236
Income		γ
	Household_Disposable_income	0.0001153	0.0001343
	Hosuhold_Disposable_income squared	-2.43E-09	2.07E-09
	Household_sizeÃ—Household_disposable_income	-1.63E-06	0.000023
Leisure		λ
	Leisure_Male	-0.0472945	0.0551945
	Leisure_Man squared	0.0014071	0.0004473
	Leisure_Woman	0.0416601	0.0425495
	Leisure_Woman squared	0.0003121	0.0002634
	Leisure_Man X Household_disp_income	1.64E-06	8.45E-07
	Leisure_Woman X Household_disp_income	1.18E-07	8.47E-07
	Leisure_Man X Age_Man	-0.0038039	0.0021464
	Leisure_Woman X Age_Woman	-0.0059885	0.0016256
	Leisure_Man X Age_Man squared	0.0000479	0.0000254
	Leisure_Woman X Age_Woman squared	0.0000904	0.0000201
	Leisure_Man X No. Children	-0.0067684	0.0038964
	Leisure_Woman X No. Children	0.0069002	0.0027455
	Leisure_Man X No. Children0-6	0.0085339	0.0051382
	Leisure_Man X No. Children7-10	0.002834	0.0060786
	Leisure_Woman X No. Children0-6	0.0088988	0.0034797
	Leisure_Woman X No. Children7-10	0.0022974	0.0039516
	Leisure_Woman X Leisure_Man	0.0002931	0.0001535
Other
	N.observations (N. couples*49 alternatives)	64435
	N.couples	1315
	LR chi2(32)	5058.95
	Prob > chi2	0
	Pseudo R2	0.4943
	Log likelihood	-2588.2705

Table A8

Maximum likelihood estimates – singles (Luxembourg)

		Male		Female
Model component	Variable	Coef.	Std. Err.	Coef.	Std. Err.
Opportunity density		δ		δ
	Employee	3.840025	1.467676	-3.83547	0.916069
	Self_employed	3.076828	1.44261	-6.09075	1.124339
	Part-time_Employee	-1.25405	0.727917	3.214104	0.688409
	Full-time_Employee	2.760224	0.389481	3.833989	0.508304
	Part-time_Self-employed	-17.2776	699.2763	2.533271	1.111393
	Full-time_Self-employed	0.139062	0.585945	2.068577	0.878229
Income		γ		γ
	Disposable income	3.53E-05	0.000416	0.00036	0.000262
	Disposable income squared	-8.96E-09	2.75E-08	-8.71E-09	9.30E-09
	Household size X Disp_income	0.000177	0.000082	-4.1E-05	5.76E-05
Leisure		λ		λ
	Leisure	0.083226	0.061447	0.222152	0.066109
	Leisure2	0.00187	0.000632	-0.00012	0.000504
	Leisure X Disposable income	2.07E-07	3.91E-06	3.42E-06	2.72E-06
	Leisure X Age	-0.0096	0.001664	-0.01311	0.00192
	Leisure X Age squared	0.000118	0.000021	0.00016	2.33E-05
	Leisure X No. Children	0.010493	0.008464	0.002518	0.005455
	Leisure X No. Children 0-6	0.006816	0.029223	0.00331	0.010569
	Leisure X No. Children 7-10	0.024772	0.029139	-0.0027	0.009811
Other

	N.observations (N. single*7 alternatives)	4123		3640
	N.single	589		520
	LR chi2(17)	1157.65		951.82
	Prob > chi2	0		0
	Pseudo R2	0.505		4703
	Log likelihood	-567.317		5335.965

Table A9

Maximum likelihood estimates – couples (Spain)

Model component	Variable	Coef.	Std. Err.
Opportunity density		δ
	Employee_Man	-0.2868366	0.2843099
	Self-employed_Man	-0.7698504	0.2931603
	Employee_Woman	-2.403139	0.252017
	Self-employed_Woman	-2.585398	0.2813223
	Part-time_Employee_Man	-0.1938884	0.1981381
	Full-time_Employee_Man	2.390778	0.1070763
	Part-time_Self-employed_Man	-1.089852	0.2490981
	Full-time_Self-employed_Man	0.9119172	0.1280802
	Part-time_Employee_Woman	1.511822	0.2167088
	Full-time_Employee_Woman	2.692898	0.1672168
	Part-time_Self-employed_Woman	-0.3884766	0.2749832
	Full-time_Self-employed_Woman	0.8462308	0.2033327
Income		γ
	Household_Disposable_income	-0.0001841	0.0001271
	Hosuhold_Disposable_income squared	2.51E-08	8.12E-09
	Household_sizeÃ—Household_disposable_income	-0.0000236	0.0000156
Leisure		λ
	Leisure_Male	-0.0294838	0.0239608
	Leisure_Man squared	0.0005993	0.0001227
	Leisure_Woman	0.0991669	0.0229826
	Leisure_Woman squared	-0.0003914	0.0001435
	Leisure_Man X Household_disp_income	5.62E-06	9.76E-07
	Leisure_Woman X Household_disp_income	1.22E-06	7.46E-07
	Leisure_Man X Age_Man	-0.0022498	0.0009384
	Leisure_Woman X Age_Woman	-0.0043625	0.0007961
	Leisure_Man X Age_Man squared	0.0000224	0.0000103
	Leisure_Woman X Age_Woman squared	0.0000589	9.11E-06
	Leisure_Man X No. Children	-0.0015521	0.0013717
	Leisure_Woman X No. Children	0.0036569	0.0011625
	Leisure_Man X No. Children0-6	0.0034279	0.0019022
	Leisure_Man X No. Children7-10	-0.0022426	0.0020741
	Leisure_Woman X No. Children0-6	0.0013244	0.0016922
	Leisure_Woman X No. Children7-10	0.0020022	0.0017517
	Leisure_Woman X Leisure_Man	0.00032	0.0000585
Other
	N.observations (N. couples*49 alternatives)	244755
	N.couples	4995
	LR chi2(32)	13049.94
	Prob > chi2	0
	Pseudo R2	0.3357
	Log likelihood	-12914.672

Table A10

Maximum likelihood estimates – singles (Spain)

		Male		Female
Model component	Variable	Coef.	Std. Err.	Coef.	Std. Err.
Opportunity density		δ		δ
	Employee	-1.30198	0.428921	-1.7268	0.428239
	Self_employed	-1.41084	0.456916	-1.59374	0.505891
	Part-time_Employee	0.607968	0.329195	1.895538	0.346785
	Full-time_Employee	2.496161	0.217392	3.236458	0.246681
	Part-time_Self-employed	-1.10093	0.419394	-0.78624	0.512791
	Full-time_Self-employed	0.757978	0.25528	1.336878	0.331166
Income		γ		γ
	Disposable income	0.000391	0.000202	0.000249	0.000234
	Disposable income squared	-2.86E-08	2.19E-08	-4.02E-09	2.89E-08
	Household size X Disp_income	3.35E-05	4.41E-05	0.000166	5.63E-05
Leisure		λ		λ
	Leisure	0.091073	0.027093	0.060002	0.028202
	Leisure2	7.25E-05	0.000216	0.000661	0.000213
	Leisure X Disposable income	2.92E-08	2.03E-06	2.06E-06	2.36E-06
	Leisure X Age	-0.00465	0.000802	-0.00588	0.000853
	Leisure X Age squared	5.79E-05	9.77E-06	6.94E-05	1.02E-05
	Leisure X No. Children	0.002815	0.0077	0.005045	0.002922
	Leisure X No. Children 0-6	-0.00077	0.015847	0.004662	0.006085
	Leisure X No. Children 7-10	-0.01601	0.021244	0.00168	0.005529
Other
	N.observations (N. single*7 alternatives)	12530		12194
	N.single	1790		1742
	LR chi2(17)	2335.29		2421.22
	Prob > chi2	0		0
	Pseudo R2	0.3352		0.3571
	Log likelihood	-2315.53		-2179.16

Table A11

Maximum likelihood estimates – couples (UK)

Model component	Variable	Coef.	Std. Err.
Opportunity density		δ
	Employee_Man	0.1010326	0.3378421
	Self-employed_Man	-0.6931103	0.3433464
	Employee_Woman	-2.125809	0.2756313
	Self-employed_Woman	-2.693189	0.3039796
	Part-time_Employee_Man	-1.045434	0.2048579
	Full-time_Employee_Man	2.390656	0.1114932
	Part-time_Self-employed_Man	-1.088571	0.24735
	Full-time_Self-employed_Man	1.330872	0.1382285
	Part-time_Employee_Woman	1.85452	0.2366666
	Full-time_Employee_Woman	2.886648	0.2010856
	Part-time_Self-employed_Woman	0.3428018	0.2863139
	Full-time_Self-employed_Woman	0.6378565	0.2530663
Income		γ
	Household_Disposable_income	0.0001122	0.0002534
	Hosuhold_Disposable_income squared	-3.40E-08	1.75E-08
	Household_size X Household_disposable_income	0.0000397	0.000025
Leisure		λ
	Leisure_Male	0.0426497	0.0280003
	Leisure_Man squared	0.0004884	0.0001547
	Leisure_Woman	0.1642487	0.0289328
	Leisure_Woman squared	-0.0006741	0.0001594
	Leisure_Man X Household_disp_income	9.12E-07	1.76E-06
	Leisure_Woman X Household_disp_income	-7.02E-07	1.45E-06
	Leisure_Man X Age_Man	-0.006004	0.0012687
	Leisure_Woman X Age_Woman	-0.0071774	0.0013197
	Leisure_Man X Age_Man squared	0.0000731	0.0000171
	Leisure_Woman X Age_Woman squared	0.0000904	0.0000183
	Leisure_Man X No. Children	0.0023683	0.0016979
	Leisure_Woman X No. Children	0.0169523	0.0016992
	Leisure_Man X No. Children0-6	-0.0029332	0.0017903
	Leisure_Man X No. Children7-10	0.0008209	0.001984
	Leisure_Woman X No. Children0-6	0.0142435	0.0019016
	Leisure_Woman X No. Children7-10	0.0034794	0.0020909
	Leisure_Woman X Leisure_Man	0.0006758	0.0000828
Other
	N.observations (N. couples*49 alternatives)	220843
	N.couples	4507
	LR chi2(32)	12926.1
	Prob > chi2	0
	Pseudo R2	0.3685
	Log likelihood	-11077.385

Table A12

Maximum likelihood estimates – singles (UK)

		Male		Female
Model component	Variable	Coef.	Std. Err.	Coef.	Std. Err.
Opportunity density		δ		δ
	Employee	-0.23213	0.467104	-2.73527	0.381373
	Self_employed	-0.73375	0.479139	-3.96636	0.455567
	Part-time_Employee	-0.48835	0.315075	2.234354	0.311484
	Full-time_Employee	2.423602	0.215381	3.217563	0.257497
	Part-time_Self-employed	-1.83573	0.404768	1.149457	0.429612
	Full-time_Self-employed	0.850365	0.26129	1.745809	0.371801
Income		γ		γ
	Disposable income	-8.1E-05	0.000262	0.001196	0.000448
	Disposable income squared	1.29E-08	3.04E-08	-1.33E-07	6.24E-08
	Household size X Disp_income	1.13E-05	5.03E-05	-1.9E-05	6.18E-05
Leisure		λ		λ
	Leisure	0.122021	0.027423	0.248225	0.030925
	Leisure2	0.00039	0.000239	-0.00026	0.00022
	Leisure X Disposable income	1.27E-06	2.44E-06	-9.32E-06	4.05E-06
	Leisure X Age	-0.0075	0.001001	-0.01234	0.00121
	Leisure X Age squared	0.000102	1.47E-05	0.000166	1.74E-05
	Leisure X No. Children	-0.00517	0.005611	0.015035	0.002616
	Leisure X No. Children 0-6	0.020995	0.012061	0.026352	0.003583
	Leisure X No. Children 7-10	0.013849	0.010819	0.004335	0.003571
Other
	N.observations (N. single*7 alternatives)	13937		17549
	N.single	1991		2507
	LR chi2(17)	2736.7		3775.11
	Prob > chi2	0		0
	Pseudo R2	0.3532		0.3869
	Log likelihood	-2505.96		-2990.84

References

1
Designing Optimal Taxes with a Microeconometric Model of Household Labour Supply
1. R Aaberge
2. U Colombino
(2006)
IZA Discussion Papers 2468 pp. 1–44.
https://doi.org/10.2139/ssrn.949195
- Google Scholar
2
Accounting for family background when designing optimal income taxes: a microeconometric simulation analysis
1. R Aaberge
2. U Colombino
(2012)
Journal of Population Economics 25:741–761.
https://doi.org/10.1007/s00148-010-0331-y
- Google Scholar
3
Using a Microeconometric Model of Household Labour Supply to Design Optimal Income Taxes*
1. R Aaberge
2. U Colombino
(2013)
The Scandinavian Journal of Economics 115:449–475.
https://doi.org/10.1111/sjoe.12015
- Google Scholar
4
Handbook of Microsimulation Modelling, Contributions to Economic Analysis
1. R Aaberge
2. U Colombino
(2014)
Labour Supply Models, Handbook of Microsimulation Modelling, Contributions to Economic Analysis, Vol, 293, Emerald.
- Google Scholar
5
Do more equal slices shrink the cake? An empirical investigation of tax-transfer reform proposals in Italy
(2004)
Population Economics 17:767–785.
https://doi.org/10.1007/s00148-004-0193-2
- Google Scholar
6
Public Economics in Action
1. AB Atkinson
(1996)
Oxford: Clarendon Press.
https://doi.org/10.1093/0198292163.001.0001
- Google Scholar
7
On Analyzing the World Distribution of Income
1. AB Atkinson
2. A Brandolini
(2010)
The World Bank Economic Review 24:1–37.
https://doi.org/10.1093/wber/lhp020
- Google Scholar
8
Simulating the future of global automation, its consequences, and evaluating policy options, Vox-Eu
1. G Benzell
2. V Ye
(2021)
9
Employment, Hours of Work and the Optimal Taxation of Low-Income Families
1. R Blundell
2. A Shephard
(2012)
The Review of Economic Studies 79:481–510.
https://doi.org/10.1093/restud/rdr034
- Google Scholar
10
Means-Testing and Tax Rates on Earnings (Mirrlees Commission Report
(2008)
London: Institute for Fiscal Studies.
- Google Scholar
11
Sufficient Statistics for Welfare Analysis: A Bridge Between Structural and Reduced-Form Methods
1. R Chetty
(2009)
Annual Review of Economics, Annual Reviews 1:451–488.
- Google Scholar
12
Shifting taxes from labour to property. A simulation under labour market equilibrium
(2020)
Journal of Policy Modelling 42:367–384.
https://doi.org/10.1016/j.jpolmod.2019.07.002
- Google Scholar
13
Five Crossroads on the Way to Basic Income. An Italian Tour
1. U Colombino
(2015)
Italian Economic Journal 1:353–389.
https://doi.org/10.1007/s40797-015-0018-3
- Google Scholar
14
Is unconditional basic income a viable alternative to other social welfare measures?
1. U Colombino
(2019)
15
Handbook of Research Methods and Applications in Empirical Microeconomics
1. U Colombino
(2021)
Microeconomic models for designing and evaluating tax-transfer systems, Handbook of Research Methods and Applications in Empirical Microeconomics, Edward Elgar Publishing.
- Google Scholar
16
Basic Income and Flat Tax: The Italian scenario
1. U Colombino
2. N Islam
(2018)
CESifo Forum 19:20–29.
- Google Scholar
17
Designing a Universal Income Support Mechanism for Italy: An Exploratory Tour
1. U Colombino
2. E Narazani
(2013)
Basic Income Studies 8:1–17.
https://doi.org/10.1515/bis-2012-0010
- Google Scholar
18
Welfare-improving income tax reforms: a microsimulation analysis
1. J Creedy
2. N Herault
(2011)
Oxford Economic Papers 64:128–150.
https://doi.org/10.1093/oep/gpr029
- Google Scholar
19
Sectoral labour supply, choice restrictions and functional form
1. JK Dagsvik
2. S Strøm
(2006)
Journal of Applied Econometrics 21:803–826.
https://doi.org/10.1002/jae.866
- Google Scholar
20
Larger Transfers Financed with More Progressive Taxes? On the Optimal Design of Taxes and Transfers
(2021)
21
On reforming the welfare system: Workfare meets the negative income tax
(1993)
Journal of Public Economics 51:119–151.
- Google Scholar
22
Capitalism and Freedom
1. M Friedman
(1962)
University of Chicago Press.
- Google Scholar
23
Exploring Universal Basic Income: A Guide to Navigating Concepts, Evidence, and Practices
(2020)
Exploring Universal Basic Income: A Guide to Navigating Concepts, Evidence, and Practices, 10.1596/978-1-4648-1458-7.
- Google Scholar
24
Is Funding A Large Universal Basic Income Feasible? A Quantitative Analysis of UBI with Endogenous Labour Supply
1. M Ghatak
2. X Jaravel
(2020)
LSE Public Policy Review 1:1–11.
https://doi.org/10.31389/lseppr.9
- Google Scholar
25
Universal Basic Income: Some Theoretical Aspects
1. M Ghatak
2. F Maniquet
(2019)
Annual Review of Economics 11:895–928.
https://doi.org/10.1146/annurev-economics-080218-030220
- Google Scholar
26
Egalitarian redistribution in the era of hyper-globalization
(2020)
Review of Social Economy 78:151–184.
https://doi.org/10.1080/00346764.2020.1714072
- Google Scholar
27
The Flat Tax
1. R Hall
2. AE Rabushka
(1995)
Stanford: Hoover Institution Press.
- Google Scholar
28
Progressive Taxation Reconsidered
1. FA Hayek
(1956)
265–284, Progressive Taxation Reconsidered, Princeton, NJ, Van Nostrand, p.
- Google Scholar
29
Th Flat Tax. Toward a British Model
1. A Heath
(2006)
TaxPayers: Alliance.
- Google Scholar
30
Optimal Income Taxation: Mirrlees Meets Ramsey
1. J Heathcote
2. H Tsujiyama
(2021)
Journal of Political Economy 129:3141–3184.
https://doi.org/10.1086/715851
- Google Scholar
31
Universal Basic Income in the United States and Advanced Countries
1. H Hoynes
2. J Rothstein
(2019)
Annual Review of Economics 11:929–958.
https://doi.org/10.1146/annurev-economics-080218-030237
- Google Scholar
32
Welfare Reform in European Countries: A Microsimulation Analysis
(2007)
The Economic Journal 117:1–44.
https://doi.org/10.1111/j.1468-0297.2007.02000.x
- Google Scholar
33
The case for NIT+FT in Europe
1. N Islam
2. U Colombino
(2018)
An Empirical Optimal Taxation Exercise, Economic Modelling 75:38–69.
https://doi.org/10.1016/j.econmod.2018.06.004
- Google Scholar
34
Welfare analysis of tax reforms using household data
1. MA King
(1983)
Journal of Public Economics 21:183–214.
https://doi.org/10.1016/0047-2727(83)90049-X
- Google Scholar
35
Sufficient Statistics Revisited
1. HJ Kleven
(2021)
Annual Review of Economics 13:515–538.
https://doi.org/10.1146/annurev-economics-060220-023547
- Google Scholar
36
Inequal Inequalities I
1. S. C Kolm
(1976)
Journal of Economic Theory 12:416–442.
- Google Scholar
37
Universal basic income with flat tax reform in France
1. R Magnani
2. L Piccoli
(2020)
Journal of Policy Modeling 42:235–249.
https://doi.org/10.1016/j.jpolmod.2019.07.005
- Google Scholar
38
Spatial Interaction Theory and Planning Models,North Holland
1. D McFadden
(1978)
75–96, Modelling the Choice of Residential Location, Spatial Interaction Theory and Planning Models,North Holland, Frontiers in Econometrics, Academic Press, p.
- Google Scholar
39
An exploration in the theory of optimum income taxation
1. J. A Mirrlees
(1971)
Review of Economic Studies 38:175–208.
- Google Scholar
40
Tax by Design: The Mirrlees Review
1. J Mirrlees
2. S Adam
3. T Besley
4. R Blundell
5. S Bond
6. R Chote
7. M Gammie
8. P Johnson
9. G Myles
10. J. Poterba
(editors) (2011)
Oxford: Oxford University Press for Institute for Fiscal Studies.
- Google Scholar
41
The Universal Basic Share and Social Incentives
1. K Moene
2. D Ray
(2016)
42
Using Elasticities to Derive Optimal Income Tax Rates
1. E Saez
(2001)
The Review of Economic Studies 68:205–229.
https://doi.org/10.1111/1467-937X.00166
- Google Scholar
43
Optimal Income Transfer Programs: Intensive versus Extensive Labor Supply Responses
1. E Saez
(2002)
The Quarterly Journal of Economics 117:1039–1073.
https://doi.org/10.1162/003355302760193959
- Google Scholar
44
Optimal Design of Means Tested Retirement Benefits
1. J Sefton
2. J Van De Ven
(2009)
The Economic Journal 119:F461–F481.
https://doi.org/10.1111/j.1468-0297.2009.02316.x
- Google Scholar
45
Responding to the crisis: economic stabilisation grants
1. G Standing
(2011)
Policy & Politics 39:9–25.
https://doi.org/10.1332/030557311X546389
- Google Scholar
46
The Precariat: The New Dangerous Class
1. G Standing
(2015)
Bloomsbury Revelations.
- Google Scholar
47
EUROMOD: the European Union tax-benefit microsimulation model
1. H Sutherland
2. F Figari
(2012)
International Journal of Microsimulation 6:4–26.
https://doi.org/10.34196/ijm.00075
- Google Scholar
48
Optimal Income Tax and Redistribution
1. M Tuomala
(1990)
Oxford: Clarendon Press.
- Google Scholar
49
On optimal non-linear income taxation: numerical results revisited
1. M Tuomala
(2009)
International Tax and Public Finance 17:259–270.
https://doi.org/10.1007/s10797-009-9119-y
- Google Scholar
50
Basic Income, Cambridge (Mass)
1. P Van Parijs
2. Y Vanderborght
(2017)
Harvard University Press.
https://doi.org/10.4159/9780674978072
- Google Scholar

Article and author information

Author details

U Colombino

Department of Economics and Statistics "Cognetti De Martiis", Turin, Italy

For correspondence
ugo.colombino@unito.it

"This ORCID iD identifies the author of this article:" 0000-0002-0194-2943
N Islam

Living Conditions, Esch-sur-Alzette, Luxembourg

"This ORCID iD identifies the author of this article:" 0000-0002-1152-8623

Funding

No specific funding for this article is reported.

Acknowledgements

We thank two anonymous referees and the participants to the Workshop on Labour Income Taxation and the Labour Supply (LISER, January 20, 2020) for helpful comments and suggestions. Ugo Colombino thanks LISER for financial and organizational support.

Publication history

Version of Record published: August 31, 2022 (version 1)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Download citations (links to download the citations from this article in formats compatible with various reference manager tools)

BibTeX
RIS

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

“Current” and optimal TTRs

Marginal Tax Rate vs. Taxable Income. France

Average Tax Rate vs. Taxable Income. France

Marginal Tax Rate vs. Taxable Income. Germany

Average Tax Rate vs. Taxable Income. Germany

Marginal Tax Rate vs. Taxable Income. Italy

Average Tax Rate vs. Taxable Income. Italy

Marginal Tax Rate vs. Taxable Income. Luxembourg

Average Tax Rate vs. Taxable Income. Luxembourg

Marginal Tax Rate vs. Taxable Income. Spain

Average Tax Rate vs. Taxable Income. Spain

Marginal Tax Rate vs. Taxable Income. United Kingdom

Average Tax Rate vs. Taxable Income. United Kingdom

France: %change of CMU by demographic group and decile, k = 0.075.

France: %change of CMU by demographic group and decile, k = 0.075.

Italy: %change of CMU by demographic group and decile, k = 0.075.

Luxembourg: %change of CMU by demographic group and decile, k = 0.075.

Spain: %change of CMU b.y demographic group and decile, k =0.075

The UK: %change of CMU by demographic group and decile, k = 0.075.

%change of disposable income w.r.t. current values by country and Kolm’s k.

Povery Gap Index by country and Optimal TTR (indexed by Kolm’s k).

Welfare Gains and Welfare Winners

“Primitives” of the economy and characteristics of the optimal polynomial TTRs

Maximum likelihood estimates – couples (France)

Maximum likelihood estimates – singles (France)

Maximum likelihood estimates – couples (Germany)

Maximum likelihood estimates – singles (Germany)

Maximum likelihood estimates – couples (Italy)

Maximum likelihood estimates – singles (Italy)

Maximum likelihood estimates – couples (Luxembourg)

Maximum likelihood estimates – singles (Luxembourg)

Maximum likelihood estimates – couples (Spain)

Maximum likelihood estimates – singles (Spain)

Maximum likelihood estimates – couples (UK)

Maximum likelihood estimates – singles (UK)

Author details

U Colombino

For correspondence

N Islam

Downloads (link to download the article as PDF)

Download citations (links to download the citations from this article in formats compatible with various reference manager tools)

Open citations (links to open the citations from this article in various online reference manager services)

Categories and tags