A Micro-Macro Interactive Simulation Model of the Swedish Economy
- Article
- Figures and data
-
Jump to
- Abstract
- 1. A microsimulation model of a national economy
- 2. Firm expectations and targets
- 3. Investment-financing - the long-range planning decision (sophisticated version, not yet in model code)
- 4. Production planning and labour demand
- 5. Labour market search
- 6. Exports, inventories, and intermediate goods (firm level)
- 7. Household consumption
- 8. Product market price determination, import competition and inventory adjustment
- Footnotes
- Appendix A
- Appendix B
- Appendix C
- Appendix D
- Appendix E
- References
- Article and author information
Abstract
Work on this micro based macro model of the Swedish Economy began in late 1974 as a joint project between the Federation of Swedish Industries, IBM Sweden and the University of Uppsala. This is an edited version of several instruction manuals I wrote for the coding and later programming of that model. It was published in December 1976 as "A micro - macro Interactive Simulation Model of the Swedish Economy" by the Federation and IBM in two parallel editions. A technical pseudo code to facilitate the final coding of the model in APL, authored jointly by myself, Mats Heiman and Gösta Olavi, was appended to that publication. This republication of the 1976 document, has been slightly trimmed, and lack the Foreword by the President of the Federation, Author’s Remarks, and the Pseudocode. The Pseudocode is however available from the Journal online as (Eliasson et al., 1976). It details the specifications and highlights the modular design of the model and should be helpful for anybody who might want to reproduce a version of the model.
Originally this model, called MOSES, for Model Of the Swedish Economic System, was designed to facilitate understanding and quantifying the role of markets and production firms in economy wide economic development. Of particular interest were the consequences of markets being disturbed by inflation. The modelling approach was bottom up, drawing extensively on empirical research in business economics, not least on my own study on business economic planning practices (Eliasson, 1976a). The model has a general design in that it integrates a standard Keynesian demand driven macro model with a Leontief type input output sector structure. The manufacturing subindustries, furthermore, are populated with boundedly rational (“ignorant”) firms (Simon, 1955; Simon 1959). These firms make up the core market governed supply machinery of the model, and integrate product, labor, and financial market considerations within their business plans. Firms compete in the markets of the model. Their plans and decisions are guided by Stockholm School ex ante price expectations and learning from feed backs of ex post outcome experiences. Schumpeterian entrepreneurs enter markets unexpectedly and compel incumbents to perform. Market competition thus self-coordinates the entire model economy under an upper technology constraint embodied in new investments of firms. The government may intervene in markets, but there are no artificial external equilibrium constraints imposed. I had no ambition to build a micro foundation of existing macro theory, neither has the model been designed to provide forecasts to support policy. The ambition has been to understand what government can do to the economy as one of many monopoly actors with boundedly rational insights.
The ambition was empirical, to begin with to reproduce and understand the long term and cyclical market dynamics of a Sweden like industrial economy. To that end a separate annual Planning Survey to Swedish manufacturing firms, tailored to the needs of the model, was started at the Federation. That survey will eventually provide statistics also to test the model’s capacity to generate distributional characteristics of the Swedish economy.
1. A microsimulation model of a national economy
This model is of the microsimulation kind in the sense of Bennett and Bergmann (1975); Bennett and Bergmann (1976); Bergmann (1973); Bergmann (1974); Orcutt (1960); Orcutt (1961); Orcutt et al. (1976) and Orcutt (1961). There is a difference, however, in that focus is on the dynamics of agents interacting both across markets and sequentially over time (dynamics), and that the micro units are heterogeneous production firms, rather than individuals and households that dominate the micro simulation literature. My main ambition is to explore the role of markets in macro-economic development. Hence, firms’ behavior is governed by their expectations about prices. In formulating the model, I have drawn significantly on the Stockholm School ex ante anticipations and ex post plan outcome feed backs that I experimented with in my doctorate thesis (Eliasson, 1967; Eliasson, 1969). In modelling firm planning I have drawn directly on my interview study (Eliasson, 1976a) of planning practices in European, Japanese and US manufacturing firms, that concludes (in chapter XI) with a proposed model of the firm. My ambition has been to parameterize the firm model as close as possible to the planning and decision parameters that firms’ top management recognizes, irrespective of how that design tallies with received microeconomic theory. The philosophy behind the model is that we need to understand how micro agents (firms, households etc.) interact in markets to understand economy wide behavior. I have no ambition to clarify the micro foundations of existing macro theory.
For many types of analysis, the conventional macro model does not allow the detail of representation we need, and especially not for representing agent and market behavior. Therefore, it becomes tempting to disaggregate into subsectors, and sub-sectors of sub-sectors. Quite soon we have a one thousand equation model that we have difficulties making intellectual sense of. Micro behavioral characteristics have been aggregated away, so has also been the competitive market machinery that governs the dynamic allocation of resources in the economy across decision units and over time. Neither do we know what the parameters stand for because of estimation problems like collinearity, feed backs within periods etc., and our subsectors quite arbitrarily cut right through the decision units.
In principle, however, there is no difference between macro modelling and micro to macro modelling. All entities in economics are macro in some sense. In practice there is a difference, however, since the ambition of this project is to take the analysis down to the level of a firm defined by its financial accounts that makes decisions in markets, and to study (1) the micro basis for inflation and (2) the interaction of firms so defined across markets and over time and how these market interactions affect inflation, profitability, the allocation of resources and economic growth. To model the role of markets in economy wide behavior mathematical simulation, or micro simulation is the only theoretical and empirical method available. While it allows realistic specification, parameter estimation becomes increasingly difficult. Since firms’ behavior, their interactions in markets, and how markets aggregate it all up to macro is beyond macro modelling, these estimation problems simply must be dealt with. Conventional statistical estimation methods will probably have to be abandoned and some other kind of calibration and inference method resorted to. I will address these problems as they come. Above all, empirically relevant specification comes first and should not be compromised to facilitate parameter estimation.
Dynamics is the difficult and most important problem. To deal explicitly with period-to-period market interactions over time a dynamic micro-based economy wide approach is necessary to capture the market allocation of resources across micro units and over time. This means that we will be addressing the perennial theme of how the business cycle interacts and affects long term economic growth, and Stockholm School ex ante plan ex post realization feed backs (this time at the micro firm level) will be the appropriate design for that.
To build a model of endogenous economic growth short term behavior in markets will not only be governing and affect the long term, but the entire model economy will be dynamically self-coordinated by the actors in the markets, a problem that equilibrium price taking, market clearing models have not been capable of addressing (Lindbeck, 1963). If we have built a model that can handle the interaction between the short and the long terms to our satisfaction it will be capable of handling several other dynamic problems as well, and as model work has progressed, we have begun to talk about understanding the evolution of a capitalistic market economy.
In order not to be overwhelmed by technical problems we have struck some convenient compromises of specification that do not - I believe - reduce the explanatory potential of the model, or limit further expansion of the model, or subject us to extreme estimation difficulties. The model has a modular structure based on my experience from the design of business planning systems (Eliasson, 1976a) that will facilitate future developments of the model. For the time being we have constructed a conventional, and in no way complex economy wide model within which a micro (firm) specified manufacturing industry operates. This approach allows us to keep our special features: namely a micro specification of the behavior of three integrated markets: The labor market, several product markets and a financial system, a bank. And these three markets, as we will see, will be integrated from period to period within the business plans of individual firms.
We must also keep in mind that the prime ambition with this modelling project is to have a richly specified model structure capable of responding to a spectrum of interesting what if questions. The purpose is analysis and understanding, not forecasting.
This first section will contain a non-formal overview of the model . There will be an account of the estimation or calibrating principles involved and a few words on the empirical philosophy or the method: Does it differ from conventional econometric method?
This first section is self-contained for those who are only interested in what the model is all about, without understanding how it functions. The following sections were originally designed as instructions for coding the model, with associated comments for possible external users .
The model has a modular structure in the sense that module interfaces are well defined and often in the form of market interfaces. Some modules can be closed, and others added without necessarily recalibrating the entire model. The firm model is a typical module, each with a well-defined market interface.
1.1. Model overview
Table 1 shows the main modules of the model and their connection with the external world. There are in practice only four sets of exogenous variables:
Foreign (export) prices,
The foreign market interest rate,
The labor force, and
The rate of change in productivity of new investments globally available,1
Model modules
| Business system (manufacturing firm model) |
|---|
| Operations planning (short term) |
| Production system |
| Inventory system |
| Expectations |
| Profit targeting |
| (Cash management) |
| Investment-Financing (long term) |
| Investment plan |
| Long term borrowing |
| Household consumption (macro) |
| Buying/consuming |
| Saving |
| Service sector (macro) |
| Government sector (macro) |
| Employment |
| Taxes/transfers |
| Economic policy |
| Note: So far only Government employment has been entered into model, and government production is assumed to be proportional to government employment . |
| Other production sectors (six sectors from input/output table) |
| Foreign connections |
| Prices - exogenous |
| Exchange rate exogenous |
| Interest rate - exogenous |
| Export volume- endogenous for each firm |
| Import volume- endogenous (macro) |
| Trade assets and debts (endogenous by firm) |
| Markets |
| Labor market |
| Product market |
| Financial market (a bank) |
| Exogenous variables |
| Foreign prices: one for each of the four sub markets of manufacturing |
| Foreign Interest rate: |
| Technology: The rate of change in labor productivity of new investment vintages. |
| The labor force. |
One can therefore say that this model economy (of Sweden) has been placed in a global (market) price system (product prices, rate of interest) and (as we will see) a global pool of new technology that firms access through their endogenous investments. The model economy is therefore populated by heterogeneous firms forming expectations about market prices that all operate sequentially under an upper exogenous technology constraint, all market prices, except the foreign ones, being endogenously conditioned by feedback experience from the realization from period (quarter) to period of uncountable confrontations of inconsistent plans in the markets of the model.
The four micro defined markets of the model operate by quarter and generate a set of future quarterly values on the exogenous variables. They are Raw materials and basic goods (RAW), Intermediary products (IMED), Durable (Investment) goods (DUR) and non-durable consumption goods (NDUR). To scale the model up to Swedish National Accounts (NA) level the remaining seven production sectors, including government production, agriculture, mining, construction, transportation, electricity generation and other services are represented in macro by their input output sectors.
To begin with, and for technical computer capacity reasons, the standard time horizon we have in mind is around five years, or one business cycle. The model runs sequentially by quarter, or a normal production planning period in manufacturing (Eliasson, 1976a). I will come back to the horizon problem below. However, even if our attention is restricted to a 5-year time span, much of the calibration work requires that we check model behavior over a much longer period (see section 3).
The best way to proceed from here is to go through the central modules of the model one by one.
1.1.1. Business sector – short run production planning
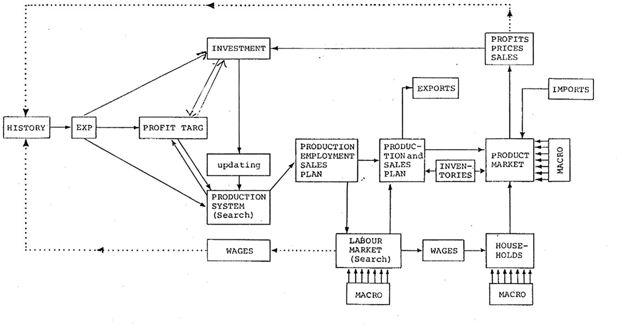
Figure 1 is a flow-chart overview of the short-term decision system of one firm. Figure 2 gives details of the production system.
The Micro Macro model has been designed on the interview experience documented in Eliasson (1976a) and reflects management planning and plan revision practices in sufficient detail to make decision parameters recognizable to top level management. Plans and decisions are based on statistical information collected from firms’ own statistical accounts in a special annual survey (The Planning Survey) conducted from 1974 by the Federation of Swedish Industries (see Virin, 1976). In Figure 1 an experimental run begins from an initial state of data collected among other places from that Planning Survey. At the left-hand side the model firm begins planning from a vector of firm {P, W, M, S} historic (5 year annual) product price, wage, profit margin, sales and capacity utilization etc data.2 The questions in the Planning survey have been formulated on the format of the model, and are compatible with the internal statistical systems of firms (Eliasson, 1976a). The historic initial state vector is converted into firm expectations in the EXP module. Here quadratic adaptive smoothing formulae are used, complemented with an error correction component and a risk aversion factor (see Section 2.3). In model simulations a complete set of new initial state data is endogenously computed from quarter to quarter. A calibrated model can therefore be run on given (known) exogenous data up to the present time and then be reloaded with new planning survey data and thus set up for new “empirical experiments”.3
The profit margin variable is translated into a profit margin target in the TARG block (Section 2.1). Profit margin targeting is modelled on the Maintain and Improve Profits (MIP) principle found in Eliasson (1976a) to be standard practice in business planning. It can be demonstrated to approximate an ex-ante wealth (net worth) maximizing principle that is revised every quarter (see reference and below). Here we also use a conventional smoothing formula. The length of historic time considered is longer than in the EXP sector.
Growth expectations feed into the investment module to generate long-term plans as explained below. Long-term expectations are also modified to apply to the next year and are fed into the production system.
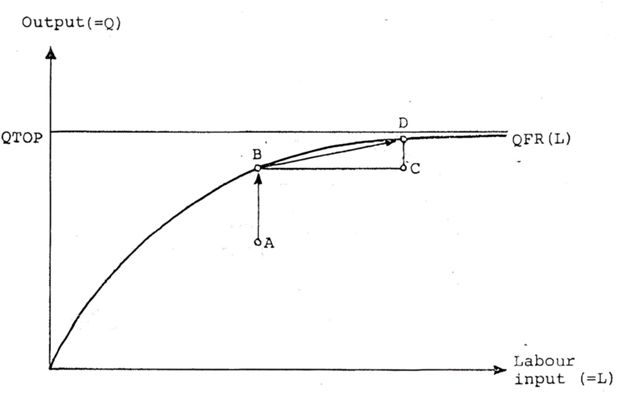
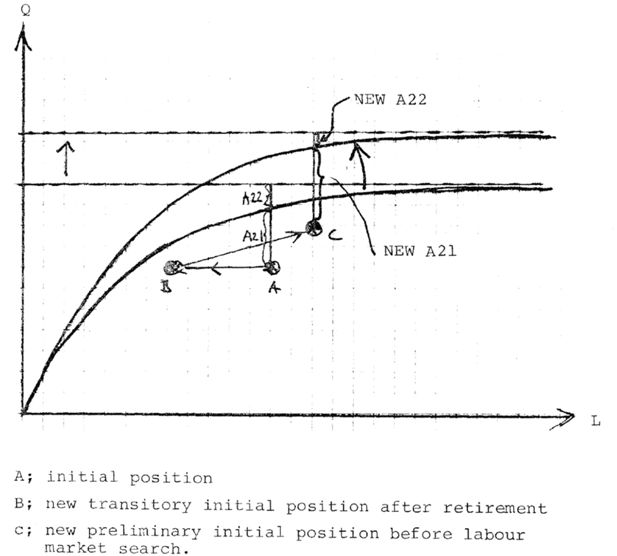
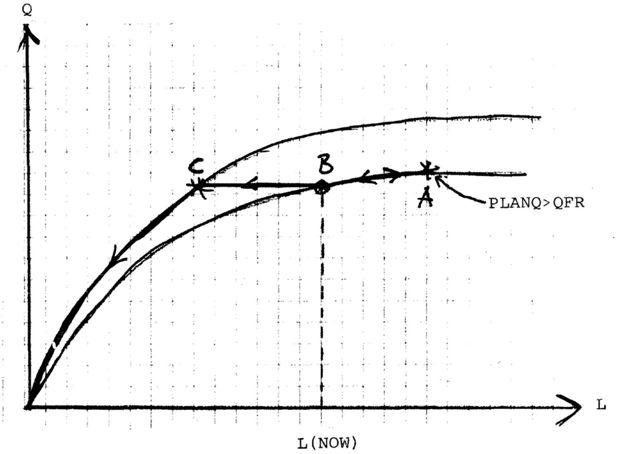
Each period (quarter) each firm is identified by a production possibility frontier (QFR(L)) defined as a function of labor input as in Figure 2 and a location below that curve.4 The distance between A and B measures the increase in output Q that the firm can achieve during the current period with no extra labor input as indicated by the L coordinate in A. In practice a vertical move between A and B cannot be costless. For the time being we abstract from that.
Suffice it to note that in those experimental runs where we have investigated this aspect there seems to be a general tendency among firms to be operating in the A, B range, which is constantly shifted outwards by investment.
The distance CD measures (for the same period) the extra increase that the firm is capable of, with the application of extra labor, but staying within a commercially viable operating range. Approximate data on A, B, C and D are collected in the annual Planning Survey for 1976 by the Federation of Swedish Industries (Virin, 1976).
The production function QFR(L) in Figure 2 is of the putty-clay type and can be directly estimated on the data collected in the Planning Survey. New investment, characterized by a higher labor productivity than investment from the period before is completely “embodied” with the average technical performance rates of earlier investments through a change in the coefficients of QFR(L).
The first sales growth expectation of a model firm from the EXP module starts a trial move from A in the direction indicated by EXP (S). After each step price and wage expectations are entered and checks against profit margin targets made. As soon as the firm M-target is satisfied, search stops and the necessary change in the labor force is calculated. If it means a decrease, workers are laid off. If an increase, the model firm enters the labor market to search for new workers (see section 4). After this search has been terminated the firm can calculate its output for the period. The wage level has been determined and is fed back to update the historic vector (dotted lines in Figure 1). The firm now checks its ex ante data against finished goods stocks to determine how much to supply in the market. A certain fraction, determined by the last period’s relative domestic and foreign prices is delivered to export markets. The final distribution between sales and inventories for each market and the price level are determined in a confrontation with inputs and household demand (middle right end of Figure 1 and lower end of Figure 3) to be described section 8.3. Final price, profit and sales data have now been determined and are fed back into the historic vector of each firm (dotted lines).
1.1.2. Labor market
The labor market process is represented in micro in considerable detail. At this level, however, requirements on relevant specification are still higher. Hence, the version now to be described should be considered provisional and experiments conducted so far have taught us that model behavior is too sensitive to variations in the random search sequences that (in combination with a small number of firms) determine how, and in which order among the firms one firm recruits.
Labor is homogeneous in the present version of the model. The productivity of one worker is determined by the machine capital of the firm that employs him, a specification that is appropriate for large parts of manufacturing, which means that labor productivity both varies a lot across the firm population and is updated for each firm each quarter (see below).
The first step each period is an adjustment of “natural” decreases in the labor force of each industry and firm unit through retirement. This adjustment is applied proportionally throughout. Then the unemployment pool is filled with new entrants to the labor market. After that the service and Government sectors enter the labor market in that order. They offer last period’s average wage increase in the manufacturing industry and get whatever is available from the pool of unemployed. This sounds a bit arbitrary, and it is. We have had to enter this specification provisionally to allow for the fact that wage and salary levels differ significantly between subindustries even though labor is homogeneous. The assumption that the export oriented manufacturing is the wage leading industry is conventional in macro modelling. It is of course not quite true at the micro level. With no explicit separation of wage levels (because of skills etc.) and little knowledge as to how the government, service and industry sectors interact in the labor market, this macro simplification will have to do for the time being.
After the service and government sectors have done their recruiting, firms enter one by one in the order by which they need to increase their labor force. They scan other firms, including the pool of unemployed. The probability of hitting a particular location of labor supply is proportional to its size (labor force and the number of unemployed compared to total labor force).
The firm offers a fraction of the expected wage increase. From the pool of unemployed people are forthcoming at the wage offered if it exceeds the unemployment benefit. If a firm is raided (for workers) by a firm with a wage offer that is sufficiently above its own, the raider gets the people it wants up to a maximum proportion of the raided firm’s labor force. The raided firm then adjusts its wage level upwards with the difference observed and revises its production, employment, and investment plans for the new data.
If a firm raids another firm with a higher wage level, it does not get any new workers but has to upgrade its offering wage level and revise its production plan for the next trial. After search is over, firms with relatively low wages, that have learned about the market wage levels around them, have had to upgrade their own wage level by a fraction of the differences observed.
Firms can be allowed any predetermined number of trials each quarter. Obviously, the size of wage adjustment coefficients and the number of trials (intensity of search) each period determines the degree of wage differentiation that can be maintained in the labor market under the homogeneity assumption. We will experiment with various impediments to this adjustment process. We can note already now that overall macro behavior of the model is very sensitive to the time reaction parameters of the labor market.
1.1.3. Business sector: Long-term investment financing (One firm)
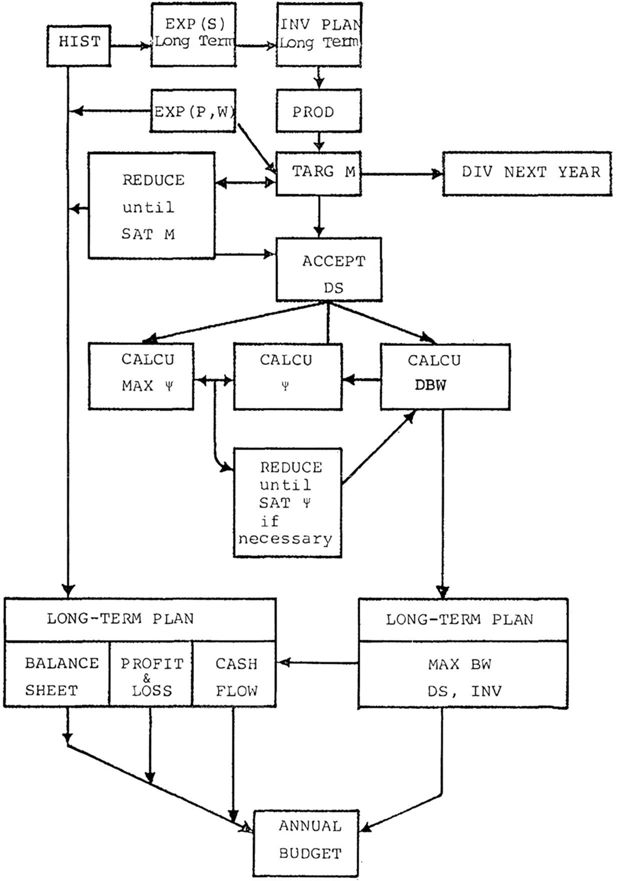
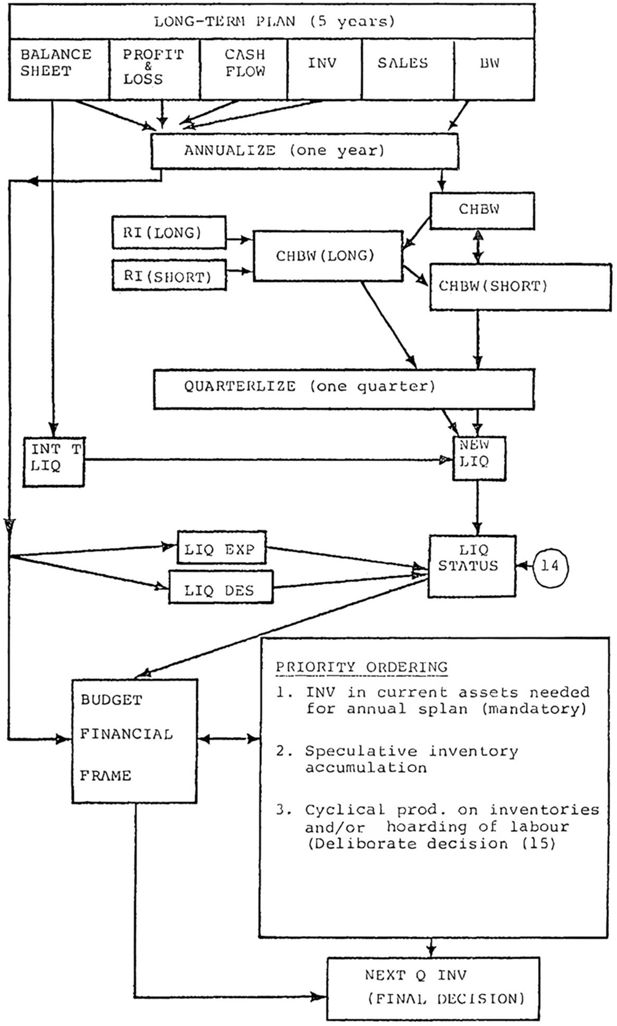
Operations planning described in the previous section and long-term investment financing decisions now to be presented are organizationally separated. The two planning decision sequences are integrated in the current (quarterly) financial plan, where the firm interacts with the short-term money market (“the bank”). This organization of decision making corresponds nicely with actual practice in large firms (Eliasson, 1976b). Throughout modelling work great care has been taken to make sure that no “leakage” occurs, and that all stock and flow accounts at micro (firm) and macro levels are consistently maintained from period to period. For the time being we use a simple investment decision routine (that is now in the program). The sophisticated, real-life imitation in the main text has not yet been codified in the program. It is exhibited in Figures 4 and 5 .
As in short-term planning a vector of historic Price, Wage, Profit margin and Sales (P, W, M, S) data generates a future long run EXP(P,W,S) vector and a long-run TARG(M) vector. The idea is that long-run expectations catch some long-run trend, that will guide investment decisions. Short-term expectations are formulated as a deviation from that trend.
Long-term EXP(S) initiates a calculation scheme that gives a preliminary investment plan. This preliminary investment plan is fed through the production system, described earlier, and combined with EXP(P) and EXP(W). There is a check whether the sales, investment plan combinations meet profit margin targets. If not, sales and investments are reduced until SAT(M) (see Figure 3). The convexity of the production system assures that corrections are downward. The long-run plan, furthermore, is based on long-run normal operating (capacity utilization) rates. Once this provisional plan has been reached, the firm has expectational control of future (5 year) profit performance. Then dividends (DIV) are decided for the next year. Dividends are fed into household disposable income.
The next step is to check the financing consequences of the provisional growth plan. A maximum gearing (leverage) ratio or the ratio between debt and net worth (ɸ = BW/NW) is currently calculated as described in Appendix C. The idea is that the ratio between the expected excess cash inflow and firm net worth determines the risk associated with new borrowing and will determine how the firm’s interest rate deviates from the local Swedish interest rate. Excess cash inflow is calculated within a typical budget framework. The maximum gearing ratio (MAX ɸ) is then assumed to be a function of the expected nominal return to total assets less the rate of risk taking and the nominal rate of interest. The expected gearing ratio (EXP ɸ) and rate of borrowing associated with each growth (S, INV) plan can then be calculated.
The provisional (S, INV) plan arrived at earlier is now checked against MAX ɸ, and modified downwards until below MAX ɸ. The convexity of the production system again means that a lower growth plan means higher M ex ante. We now have all the data needed to build a long-term plan around the conventional budget framework; a set of future balance sheets, a 5-year profit and loss statement and a 5-year cash-flow chart.
To be noted is that no decisions have been taken so far, except those related to fixing numbers in the plan.
We have now arrived at the investment plan for the annual budget. This is shown in Figure 4. The first year of the long-term plan is separated out and modified to fit next year, e.g., with respect to the expected business cycle. The format is the same as for the long term plan, but more details enter.
It is now time for planners to assess the credit market situation. The long-term and the short-term interest rates are compared with total borrowing requirements from the long-term plan. This decides long-term borrowing for the year. Note that this is the first decision to act that has been taken so far in long-term planning. It has been based on expected market prices, and therefore represents an instance of price setting autonomy, and a departure from the price taking assumption. This means that short-term borrowing is either planned to be reduced or increased at the going short-term interest rate to make up for the estimated difference in the annual budget.
Next, the annual budget is broken down into quarters.
The initial liquidity position is compared with the new liquidity position based on the first quarter of the annual budget. These data are in turn compared with expected liquidity over the budget and long-term plan and compared with desired liquidity. From this the financial frame of the budget per quarter is derived.
Mandatory requirements on finance from working capital etc. are subtracted. After this, what is left is allocated to investment spending. The decision is now final for each quarter. This corresponds to what is called the appropriations procedure in budgeting practice (Eliasson, 1976a).
New investment brings with it global best practice technology, which defines an upper boundary on productive capacity of the firm. The way investment affects the production system is described in section 4.
Also note that budget assumptions may go wrong ex post. The buffer that takes up the needed adjustment is liquidity and/or short-term borrowing.
1.1.4. Household consumption
For the time being the household sector is specified in macro. We need however gather up all incomes generated in production and feed them back through the tax and transfer system and through households and the public sector as demand in a stock flow consistent manner. The household module has been prepared for an easy transformation into micro in the sense that macro behavior will be assumed to be formally identical for each micro unit (household), the only difference being the numbers we place on various behavioral parameters. The prime reason for staying at the macro level is empirical. There is practically no micro data for Sweden available on which to build a sector with heterogenous households. This is in marked contrast with the situation in the U.S., where practically all work in microsimulation has been conducted on the household sector by Orcutt and others. Besides, the author himself does not have the same kind of background experience on studying households as he has on manufacturing firms.
The consumption function is a Stone (1954) type linear expenditure system with some non-linear features added. Basically, the household is seen as a combined consumer, saver and investor governed by a Friedman (1957) type permanent income consumption propensity under a Modigliani – Modigliani and Brumberg (1955) life cycle plan. One technical novelty is that saving is treated as a future consumption (spending) category in that households aim to keep a desired financial wealth that is proportional to disposable income. Even though that doesn’t come out explicitly in macro, and may sound odd for a household, households will then have to aim for having a positive wealth balance at the expected “end of its life” for precautionary reasons. There is also a direct short-term interaction (swapping) between saving and spending on household durables, entered as a function of the rate of interest, inflation, and unemployment changes (see Section 7).
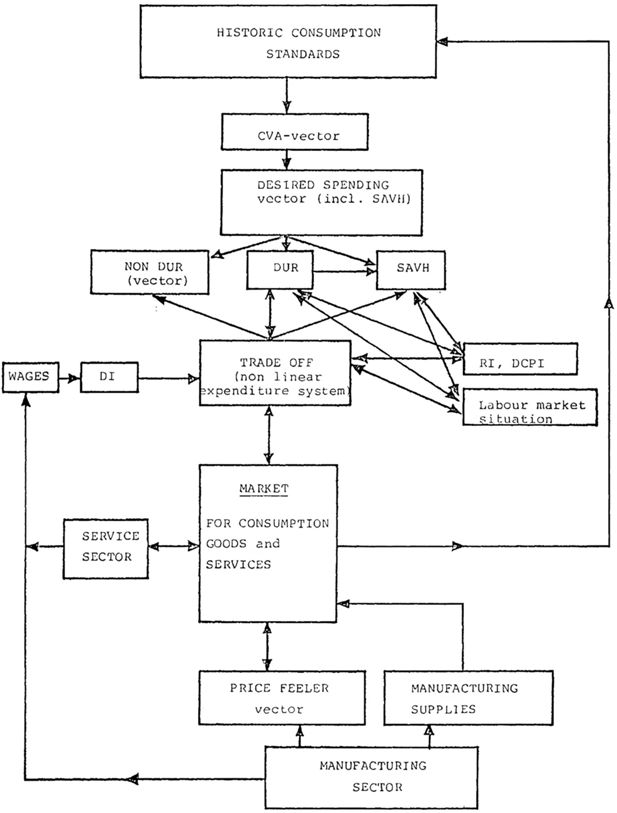
The household spending decision is described in Figure 3. Each period a vector of historic consumption data is transformed into a vector of addicted spending levels which in turn are translated into desired spending by nonlinear transformations. Desired spending is decomposed into several kinds of nondurable consumption (including services), durables and “saving”.
In another end of the model the manufacturing, service and Government sectors generate income that after being taxed feeds back into households as disposable income.
There finally remains a residual (positive or negative) between desired spending and disposable income. This residual is allocated on different spending categories by way of marginal elasticities that differ from those that divided up total desired spending.
This is the way product market dynamics takes place. Firms send out price signals and announce their supplies at those prices. Households signal back what they will buy at these prices and there follows a predetermined number of artificial market confrontations before any trading takes place. The last price signal vector then becomes the ex post price for the period (quarter), and firms split their available output between domestic sales, exports and inventories on the basis of this price. When firms decide on preliminary supply volumes to offer in the market, they each check back at their finished goods inventory positions. The guiding principle is to maintain the price level that has entered the production planning-supply decision and to try to move inventories towards “optimum” levels within a predetermined min-max range (see Section 8).
1.2. Supply and demand market non clearing dynamics
Interesting economy wide dynamics arises when ex ante incompatible supplies of heterogeneous firms and demands are confronted in the three markets of the model, during periods and between periods (quarters), and firms constantly must revise their plans because of mistaken expectations. This dynamic relates to the ex ante ex post dichotomy of Stockholm School economists that I used to “explain” revisions of investment plans by firms in my doctorate thesis (Eliasson, 1967; Eliasson, 1969). The non clearing market dynamics that arises at the micro level is no transparent analytical story, and it should not be made up as such. We have learned about its economy wide importance through simulation practice when trying to calibrate the model. Only in the very short run, we have understood, is it acceptable to abstract from market price quantity inconsistencies that keep markets from clearing. They are everywhere present but tend not to go away and often cumulate into major economy wide change. As you experiment with the micro to macro model you learn how to identify the origin of consequent economy wide changes, that as a rule have been found to have empirically reasonable explanations, thus our emphasis on empirically relevant specification, high quality data and proper parameter calibration. Familiarity with some details of the model is however needed to understand the nature of this complex market interaction dynamics, so I will come back to it in Section 8 when the whole model has been presented in sufficient detail. One example could however be mentioned already here, since it can be analytically predicted, and may be important, but was discovered when preparing for some experiments aimed at establishing the market relationships between technological change on the one hand, a micro level phenomenon, and macroeconomic growth and employment on the other. Since firms are constantly operating way under their potential (section 1.1.1. and Figure 2), and with equipment that is far below the best practice productivity standard that comes with new investment, as our statistical data show, the question constantly popped up; Why not force firms to raise output, or shed redundant workers to raise profits. As the model has been designed it all depends on how markets that relate technology and employment to economic output function. So, the natural way to enforce that outcome in a model with explicit markets and empirically well documented firm behavioral characteristics, is not to change firm behavior, but to raise market competition. What happens, for instance, if some managers in the most profitable firms try to capture the potential profit opportunities of available new technology by raising investments and their rate of recruitment of additional workers. This not only increases their growth, but raises competition with other firms for limited resources, and forces other firms to react in order not to be forced out of the market. If all firms try to outcompete each other through investing and recruiting workers from each other, prices on inputs, and notably wages, will be bid up and stop the process long before all workers have been hired by the most productive firms, and the most productive firm has substituted the globally best technology (through investment) for its existing production equipment. So that “neoclassical optimum” is unreachable in the short run because of steeply increasing costs trying to reach it. But since remaining incumbents have now upgraded their technology (productivity) performance, and even more productive new technology will become available through new investment, the next period will offer even higher levels of technology for everybody to learn from and access through new investment. The “optimum neoclassical “state of the economy will therefore still be as unreachable as before, not only because of the steeply (endogenous) cost increases experienced in trying to reach it “immediately” , but also because (endogenous) structural change has altered its location . In neoclassical terms, trying to exploit the technological opportunities too fast, model firms run up against steeply diminishing returns, but the explanation is not neoclassical and a property of the production function, but depends on steeply rising market transactions costs in trying to get there too fast. Over the longer-term investments and the introduction of new technology in all firms caused by increased competition will however represent a collective body of new technology for firms to learn from that gradually lifts the short term constraint. In models without markets, such as traditional neoclassical macro sector models, for instance the Johansen (1960) sector model “of economic growth”, that lacks markets, that explanation is lost. It makes sense in future simulation experiments to keep our eyes open for these effects, since our micro based macro model will not only generate new economic phenomena, perhaps not thought of before, but also allow new and economically more relevant explanations.
1.3. Estimation method
Even though based on a micro foundation this model addresses typical macro-economic systems problems, related to inflation, the allocation of resources and the determinants of economic growth.
The advantages of the micro to macro approach are many. We can move specification down to typical decision units (the firms) instead of having to deal with relationships between statistical artifacts at aggregate levels when it comes to observation and measurement. We can draw upon the wealth of high quality statistical micro information that exists in firms. We don’t have to make obviously false ceteris paribus assumptions associated with partial models. We introduce measurable concepts that are well known and easily understood, several of them being decision parameters that firm managers recognize and know how to use. Above all, we have designed a consistent “measuring grid”, a taxonomy, by which micro statistics are organized consistently within the framework of the national accounts. This reorganization of a consistent micro to macro database featuring both stocks and flows has already been found worth the modelling effort, by making the model useful for statistical organizing purposes.
With the higher ambition to eventually use the model for empirical studies on the Swedish economy, this approach presents us with one large obstacle. Realism in specification in combination with explicit modelling of dynamic market selection means selection based economic growth and an initial state dependent and highly nonlinear model. This necessitates that we at least for the time being give up on well known, standard econometric estimation techniques, as far as several sections of the model go. In a way, however this is a common experience with practically all large-scale macro models, only that initial state dependent nonlinear models based on selection make the problems much more difficult. There is however one decisive advantage with microsimulation modelling. All models are based on a priori specifications that condition estimated parameters, as well as the interpretation of empirical results. A well-researched prior specification of the model, as in our case, therefore, enters as exogenous and reliable information and should, in that respect, make estimated parameters more reliable, even though more difficult to obtain. When the estimated parameters cannot be stochastically interpreted, we talk about calibration, and we must decide for ourselves on the relative importance of relevant specification and reliable parameter estimates when interpreting the simulation results.
Our model is primarily designed to address problems related to the behavior of the macro economy. This means that its use should in principle be up to the same requirements as those of conventional macro models. This might, however, erroneously be taken to mean that requirements on relevance in micro specification are less demanding in macro modelling than in our micro to macro model. Quite the opposite. The main ambition of our entire modelling project is to understand how an economy can be self-coordinated by agents competing in markets, all taking place under an upper technology constraint (see below). Hence, firm behavior in markets will have to be explicitly represented and modelled, and in future hopefully also households and individuals. Macro models have nothing to say about this. Only if those micro specified market selection phenomena can be demonstrated to have a negligible influence on the behavior of the economy at large could one be satisfied with simple macro relationships. But before you hasten prematurely to such an assumption you must study the relevance of that simplification, at least theoretically. And that can be done by studying the mathematical properties of our model through simulation analysis. Early trial simulation experiments also suggest that it is not acceptable to neglect the role of markets and selection in macroeconomic behavior. Micro and markets seem to matter significantly for macro. Our modelling ambition therefore appears to make sense, and macroeconomics perhaps be in for a future problem of irrelevance.
All economic models are partial in some ways, and the art of economic analysis is to choose a partial model where all relevant aspects of the problem to be solved have been incorporated a priori. The modular specification of our micro to macro model, and the sequential relationships between modules mean that perhaps in future we might be able to device methods to estimate modules, or clusters of modules separately, and then assemble them into a whole, and that we don`t have to get the full possible micro specification right in the first implemented version of the model. The design of the model can be continuously improved as we learn more from its general theoretical properties and get more test data. Such is at least the modelling strategy. As we confront the model with new empirical data it becomes important that we find a method to discard incorrect alternatives only, without running the risk of throwing out correct alternatives. This also means that the modelling effort has been defined as a never-ending experimental process that is continually improved - or abandoned - as it is confronted with new test information. By this reformulation we have made a virtue out of the estimation difficulties.
The estimation problem has, however, to be faced squarely when it comes to quantification. A forecast had better be quantitatively right, and even though Friedman (1953) argued that the model was OK if its forecasts were correct, this cannot be taken seriously if you want to understand what you are doing. And a model that has generated correct forecasts for some time might be entirely wrong the next time, and if that matters for your decision, you had better understand that ahead of time. Beliefs are also a private problem. Beliefs certainly enter all decisions. When it comes to convincing outsiders, they must believe in what you advise. Empirical credibility becomes an issue, as for instance in economy wide cost benefit analyses of politically sensitive decisions to be taken, for which the model we are now putting together should be a superb tool (Winkler, 1967). What happens to the economy if you do this? Following a generally agreed on estimation or calibration protocol will therefore be a credibility issue in the longer term, however well specified the model.
Right now, the empirical issue however is how to calibrate the parameters of the model to be able to meaningfully study the theoretical properties of a complex model that resembles a Sweden like advanced industrial economy. And that is difficult enough. Several combinations of parameters should be expected to generate model output that resembles the numbers generated by the Swedish economy. Statistical testing of well-defined parameter combinations against historic data from the Swedish economy should be the method to discriminate between them. Fortunately, perhaps, our experience has not been of that kind. We have rather found it difficult to find one good alternative. Hence, we must turn our problem formulation around again. For those specifications that we are, so to speak, satisfied with in terms of their ability to trace economic development well, we must devise techniques to check that we have not happened to come upon a specification that is incorrect. And if we happen to find several specification alternatives among which we are unable to discriminate, we simply need more empirical data to choose. Thus, for instance, inflation is currently a great policy concern. We have also found that inflation tends to feed through model firms' expectations, and not only affect their production, recruitment and investments, and their willingness to raise wages, but also tend to get stuck in, and even overrshoot in future periods' expectations. To understand this economy wide market dynamics better and to help calibrate the model an econmetric study has been carried out at my Federation department Genberg (1975). Implications are that the macroeconomic risks of inflation do not only run through wages, as suggested by partial macro models, but also, and perhaps more importantly for the longer term, distort investment decisions and the allocation of resources. Search techniques to fit simulation models automatically to test data have been developed for simple cases (see Powell, 1964; Powell, 1965). To begin with we are working with a similar hands on manual calibration procedure (see 1.3.3 below), but hoping to come up with a more sphisticated computer based method in the future. In science, as in decision making, it is often far more important to see clearly what one doesn't know, than to be able to account for one’s knowledge. Hence the importance of getting the specification of the model right. This is also the way we go about estimating the parameters of the model.
Since the short and the long terms cannot be kept apart, as is commonly assumed to be possible in comparative static analysis, a different and more difficult comparative dynamics problem must be addressed. We have found through experimentation, however, that some sets of parameters have a unique influence on long-run trends, others on cyclical behavior around these trends and others again operate both in the long and the short run. We have used this experience to devise a two-stage parameter calibration procedure.
The first step is to calibrate the model so that it traces a chosen set of long-term trends of the Swedish economy, disregarding altogether the cyclical aspect. Figure 6 gives the reference trends and tracing performance of some recent experimental runs.
The second stage involves tracing the cyclical behavior of the same variables satisfactorily.
The two-stage procedure, calibrating short term and long-term parameters separately that we have found workable, also tallies well with how to causally interprete the endogenous growth cycle generated (Wold, 1969), and thus with our two original problems. The diffusion through the economy of inflation is of a cyclical nature, while the relationship between inflation, profits and growth are a long-term concern. Since inflation causes disorder in market pricing and affect price predictability negatively the short- and longer-term concerns are however compounded over time in intricate ways. Since studying the economy wide consequences of this complex market dynamics was the reason for starting this modelling project to begin with, the consequent empirical problems simply have to be dealt with. It is also well recognized that such complicated relationships cannot be represented in macro models. Lags between cause and effect are long, involving intricate short-term feedbacks between actors in markets and over time integrating experience, expectations, plans and realizations. This means that macro aggregates are a blend of firms in different stages of development that conceal the dynamics we are interested in.
Again, the first calibration stage, mentioned above, (satisfactory trend tracing) is all we need to handle our second problem.
1.3.1. A priori assumptions
mpirical information enters the model in seven ways:
The causal ordering of decision and activity sequences (see e.g., Figure 1) has been modeled on what we know from the interviews of Eliasson (1976a).
Structural parameters, for instance defining the relation between maximum possible inventories and sales, or trade credit extensions associated with a given value of sales.
Time reaction parameters that regulate the market dynamics of the model economy, for instance those regulating how historic experiences are transformed into expectations and plans and how fast decision makers (firms) respond to expectations that do not come true. The role of expectational mistakes in shaping future decisions becomes an issue.
Initial state data, such as firms’ capacity utilization and capital stock data collected in the annual Planning Survey of the Federation of Swedish Industries (see Virin, 1976), and corresponding stock and flow macro data from public NA statistics. All initial state data are endogenously updated from period (quarter) to period during simulations. This means that the simulation can be stopped any period, and a new initial state is available for the simulation to continue.
Start-up historic input vector, for instance, for instance a profit margin history to generate next period profit target. Also available each year from Planning Survey.
Macro parameters (for instance in consumption expenditure system, from Klevmarken and Dahlman, 1971).
Exogenous data inputs: export prices, foreign interest rate, productivities of global best practice investments, and labor force.
We consider the specification under §1 to be of critical importance as it represents a measurement taxonomy that maps one- to - one into firms own market oriented statistical measurement (information) systems. The ambition here has been to bring statistical categories as close as possible to what business decision makers look at (as studied in Eliasson, 1976a), rather than what policy makers look at. This has caused some problems of consistency when (under §4) the initial state data are aggregated up to the Swedish National Accounts level where the statistical taxonomy is production rather than market oriented (See below). The causal ordering of decision sequences under §1, furthermore, has allowed us to replace several time reaction parameters (in macro models) with directly observed decision and selection sequences in firms. Thus, for instance, firms exit at the latest when they have legally run out of equity, or earlier when their returns to equity have been running below the interest rate for many years, if, in the latter case, the firm has a management parameter that instructs it to do so. Remaining asset values are then sold in the investment goods market, or (for inventories) in product markets, loans repaid and remaining positive equity values added to household disposable income.
For the time being we focus on calibrating the time response parameters under (3) that regulate how markets affect economy wide behavior and on which we have practically no external knowledge to draw on except trying out various sets of combinations to see to what extent the model reproduces historical trends and cycles of the Swedish economy.
1.3.2. Data base needed
Two sets of data are needed for that; one set to operate the model and another to assess performance; (1) macro statistics from the Swedish national accounts (NA) that will uncritically be said to represent the Swedish economy, and (2) the panel of firm data that will become available with time from the annual Planning Survey.
The second set is specific to our model. We need a micro firm data base of at least 5 years (historic annual panel data) and a set of positional data for the initial year to get the model started. And we need a forecast or an assumption (or historic data if we trace history) for the exogeneous data for the simulation period. We would also like to be able to start simulations at a date of our choice, which means that the micro data base should, preferably, stretch far back in time. In practice this means that except for the last few years, we will not have all the data we need.
Model building, model calibration and data collection must take place simultaneously. Thus, much of the data we need for testing the model will not be available until most of the calibration work has been done. This is how we “solve” this dilemma.
Until now we have experimented with the model on historic, five-year input vectors for the years 1970-74 for each firm. Fortunately, 1974 is the peak of an inflationary profit boom in the business sector. A simulation run then begins under conditions that are like those prevailing during the year when our historic national accounts test data begin, namely 1950 (the Korean boom).
In the beginning calibration was mainly concerned with setting the model up to become operational, and we were satisfied with creating a synthetic micro database. For the time being macro subindustry data for 1970-74 (four subindustries) have simply been chopped up into 50 firms applying a random technique that preserves the averages of each subindustry. Based on this start-up information, we have performed a series of preliminary calibration experiments according to a procedure to be described below. Occasionally we have included one or several real firms in a simulation run to see what happens to them.
The next step, not yet embarked upon, will be to prolong the micro database back in time, using essentially the same synthetizing technique but also enlarging the number of firms. There are two reasons for this. We must check the stability properties of the model economy when we vary start-up data by moving back and forth over historic time. In addition, we need better and more precise historic test data to evaluate model macro performance. The changeover to this database will take place at a time when a new, extended version of the model is planned to be ready. We expect that several parameters of the system will have to be recalibrated after this changeover before the model has found its way back to a good trend tracking performance of the quality already achieved under much more primitive conditions.
The final stage is to feed the model with a set of real firms and to apply the same synthetizing technique on the residual that remains between the subindustry total and the aggregate of the real firms in each market. We are thinking in terms of eventually having the 200 largest Swedish firms in the model. When and whether we will reach that ambition, or higher, depends not only on the amount of work associated with arranging a proper database, but also on the exact nature of internal memory limitations on computer capacity. For various reasons this stage will be reached late in the project. We are currently experimenting with a sample of 50 firms.
1.3.3. Calibration
Calibration must be defined in at least two dimensions. We need a set of criteria for a good “statistical fit”.
In econometric terms this corresponds to choosing the level of significance and to some extent the estimation method. Second, we need a procedure of selection that guides us towards a specification alternative that satisfies our criteria and (NB) that is not a spurious one. These two steps are summarized in Tables 2 and 3.
Step wise master criteria for statistical fit.
| A. | Certain macro industry trends approximately right (Within 1/2 percent) over a 20 year period (see trend chart Figure 6). |
| B. | Same trends for the four sub industries. |
| Same criteria for 5-year period. | |
| C. | Micro. Compatible with “stylized facts”. No obvious “misbehavior”. |
| D. | Identify (time reaction) parameters that work uniquely (or roughly so) on cyclical behavior around trends. |
Calibration procedure (trend fitting)
| 1. Find first reference case. Assess its performance in terms of A in Table 3. |
| 2a). Perform sensitivity analysis with a view to finding new specifications that improve performance in terms of A. |
| 2b). Ditto with a view to investigating the numerical properties of the model within a normal operating range (analysis). Check and correct if properties can be regarded as unrealistic. |
| 2c). For each new reference case, repeat the whole analysis of 2 b) systematically. The purpose is to ensure, each time, that the new reference case is a better specification and not a statistical coincidence and that the properties of the system revealed by the sensitivity analysis above, and judged to be desirable, are presented in the new reference case. |
| 2d). Subject model to strong shocks. Check for “misbehavior”. (For instance, fast explosive or strong contractive economy wide behavior that have been generated by external shocks that may be considered extreme. If so, ponder the possibility that the model may generate empirically reasonable surprises that have not yet been observed. |
| 3. Define new and better references case. Repeat from 2. |
-
*
Find first reference case. Assess its performance in terms of A in Table 2.
The annual Planning Survey of the Federation of Swedish Industries has been designed to provide the panel data needed on individual firms to make calibration of micro distributional characteristics possible. We have, however, no ambitions to predict individual firm outcomes.
In general, we are not interested in using the model for routine forecasting of the business cycle forecasting type. On the other hand, we consider it possible in the future to ask questions to the model of what happens to the macro model economy if a major micro intervention in markets is enacted. This is of course also a forecast, and such model-based cost benefit studies should be contemplated when a satisfactory parameter estimation technique has been developed. Also, very interesting and meaningful in the future should be to study how specially designed individual firm models behave under different environmental circumstances that the model will be capable of generating.
We may say that the model we have designed is a combined medium-term growth and cyclical model that only requires that it tracks Swedish macro trends well over the medium-term, say five years, and exhibits a typical business cycle, but not necessarily a historic Swedish business cycle. With these “empirical” criteria we may not have moved far beyond a theoretical inquiry into understanding the interaction of inflation and growth. Since this interaction occurs (in the model) through the intermediation from period (quarter) to period of explicitly modeled markets we don’t have to be overly unassuming about having addressed an important and neglected empirical problem.
Towards the end of the project we also hope to be close to the following model performance; a specification that traces five year macro trends in Sweden according to A (in Table 2) well, irrespective of where in the period 1955–1970 we begin the simulations (provided we have the necessary start-up data), and that also reproduces a typical business cycle in all the variables in A, given exogenous variables, including policy parameters and start-up data.
This introduction has outlined the ideas of the modeling project. Next follows a formal documentation of the model specifications, to be converted into pseudo computer code, and finally into a computer language, APL.5 For an empirical understanding a more detailed account of the calibration method is needed, as well as a full description of the experimental runs. The material for that is not yet ready.
2. Firm expectations and targets
I specify the system of routine management of existing operations of a manufacturing firm. The primary source of information is my own interview study of business economic planning (Eliasson, 1976a) that concludes in Chapter XI with a sketch of a firm model. I begin here with specifying the algorithms that determine how expectations and targets are formed based on experience, external information, and on how profit targets are determined. It is basically a "looking in the mirror" adaptive approach to the future of a boundedly rational firm in the sense of Simon (1955) and Simon (1959), complemented with the possibility to use external information, for instance learning from other firms, or from external forecasts. It should also be possible to use this external slot to investigate the systemic consequences of noise input into the economy of the kind done before by Frisch (1933). The difference between our model and the other two is that disturbances in our case are transmitted into the economy by way of price changes in product, labour and financial markets, that are integrated from quarter to quarter in the formation of expectations and business plans of individual firms, not as an external knock on a mechanical system of difference equations.
As far as I know, no one has yet modeled endogenous change in existing economic structures caused by market competition and price change, or the introduction of new activities in the form of Schumpeterian entrepreneurs. The reason of course is the almost complete lack of generalized empirical knowledge about these matters, but also the limitations of expression imposed by the standard math commonly used in economic analysis. Hence the use of mathematical simulation or micro simulation in this modelling project is a methodological innovation that has expanded the range of theoretical expression, very much in the spirit of Koopmans (1957), who concluded that the modern computer might “well restore the numerical example to a position of honor among tools of analysis in regard to problems too difficult for more general solution”. We will see how much methodological controversy must be overcome to bring that understanding into economic theory (. Interdisciplinary travel seems to have given rise more to personal problems than to praise of those who have tried. Third, economy wide models I have seen have no interface to accommodate an empirically meaningful entrepreneur. We will however try, and it can be done with the market-based model specification of this model.
We distinguish between long-term expectations, on the one hand that feed into long-term plans, notably investment-growth plans, and affect the long-term financing decisions as described in the next section. On the other hand, we have short-term operating expectations that affect production and sales decisions.
Expectations focus on market prices, wages, sales and to some extent interest rates.
Firms’ targets focus on profits only, more specifically on profit margin targets determined in each firm to correspond to a rate of return target. I found the targeting procedure, that I call Maintain or Improve Profits (MIP) targeting, to be widely practiced in the US, European and Japanese firms interviewed in Eliasson (1976a). Long- and short-term targets are in principle the same, except for the time horizon, only that short-term targets may be temporarily violated under a longer-term target constraint.6
Time has three dimensions:
The long term focuses on a trend and implies a continuation beyond the long-term horizon (H).
The short term, which for us is synonymous with the (annual) budget horizon, and allows for business cycle considerations.
Updating of targets and expectations each period is based on the current feedback of targeting and expectational experience.
Targets are set once a year in the annual planning sequence.
2.1. Profit targeting (TARG-module)
In this section we introduce a set of decision criteria for the firm. They are based on a dominant objective function that condenses the preference structure of Corporate Headquarters (CHQ) of a (large) firm. We begin by identifying this function in operational terms, and proceed to particularize a set of decision rules (restrictions).
2.1.1. Objective profit function
Profits are the dominant goal variable of CHQ that guides downstream decisions in a large firm as reflected in their internal economic planning procedures (Eliasson, 1976a), implying that all other variables are subordinated the profit objective.
Such plans recognize how the certainty of information fades with future time, and hence must be complemented with routines to flexibly cope with errors. This flexibility is achieved with period-to-period revisions of anticipations and plans. There are quarterly revisions of operational budget decisions (for instance recruiting), and annual revisions of long-run, sometimes irreversible commitments (investments).
Since this is the first place where symbolic language enters, a few points on notation should be mentioned.
The APL language that we use for programming only takes ordinary letters. Systematic use of only such letters makes reading very slow. To keep good correspondence with the pseudo code and this explanatory text and to make these chapters readable at reasonable speed we often use Greek letters here, but spell them out in the pseudo code. (Hence α becomes ALFA in the pseudo code). Also note that we often use the Algol notation: = that stands for “make equal to”.
Indexes etc. are always kept on level with other symbols. Only when necessary to avoid confusion, brackets are inserted to separate symbols.
CH in front of a variable always represents the time difference or differential. Hence CHP(DUR) means ∆P(DUR)≈ (dP(DUR)/dt).
A D in front of a symbol, or a set of symbols means relative change. Hence, DNW or D(NW) means CHNW/NW.
Functions are also, and conventionally, indicated by brackets as QFR(L) that defines the production (of Q) possibility frontier (QFR) as a function of L. It will always be obvious from the text or the context when we are indicating a function.
Finally note the fact that Q both stands for quarter and output. QQ means quarterly production volume. Fortunately, in most of this explanatory text it won't be necessary to distinguish between periods of various lengths.
A consistent accounting system allows us to derive the following additive objective function):
A =M∙α - The profit contribution from manufacturing operations
B = -RHO∙β - Accounting charges
C = +DP(DUR)∙β - Capital gains from asset management
D = +(RRN- RI)∙Ѱ - Profit contributions from finance and cash management
The target variable for top Corporate Head Quarter (CHQ) management:
or the real, annual creation of asset wealth.
GOAL hence stands for the rate of increase in firm net worth (NW) plus the rate of dividend payout of that net worth (=Ɵ) both deflated to real terms by a price index, in this case the rate of change in the consumer price index (DCPI). Inflation is no minor factor to consider when designing rational profit targets for a firm (see below) and in interpreting market price signals (see below under expectations).
Each component in (1) thus adds linearly to GOAL fulfilment. A stands for the contribution from operations management to overall growth in firm value, B from “accounting”, C from asset management and D from financing (the leverage factor). We have a problem with how to define asset values under C. They can be expressed in both market and accounting (replacement cost) terms, and at book values, and firms’ target criteria are not always consistent. The strict linearity of the targeting principle in (1) is often violated in one important aspect. Capital gains that appear under C and the financial leverage factor D may be mutually dependent in that firms may find it profitable to invest in non-production (“financial”) assets to enjoy financial gains under C by borrowing under D to benefit from an interest rate that is lower than the rate of return of the firm ((RRN - RI) 0). This interdependence between the C and D components in the profitability target (1) is an important organizational concern. The fact that large firms engage significantly in non-production activities also affects the data that is collected in the Planning Survey.
A proof of (1) follows in Appendix A.7 The variables are defined verbally and in operational terms as follows:
NW = Net worth defined residually as shown in Figure 7 in the next section.
Ɵ = The rate of dividend (DIV) payout of NW = DIV/NW
α = S/A
S = Sales expressed in current prices
AS = Total assets, valued at replacement costs
β = K1/A
K1 = Replacement cost of production equipment as defined in the balance sheet. It is updated as shown in Section 3.4 below.
W = Wage index
P = Product price index
CPI = Consumer price index
RHO = Rate of depreciation of production equipment (K1).8
K2=AS-Kl= Other assets (inventories, extended trade credits, cash etc.9)
Ѱ= BW/NW = the debt (BW) net worth or gearing ratio
NW = AS - BW
RI = Rate of interest
M = Gross profit margin in terms of sales (S)
RRN= [M∙S-RHO∙K1 + K1∙DP]/AS= nominal rate of return on total capital(=AS)
RRNW = [M∙S-RHO∙K1 + K1∙DP - RI∙BW]/ NW = nominal rate of return on net worth or equity.
We assume here that all stock entities are valued at current replacement costs. This means that firms’ net worth (NW) has been obtained by a consistent (residual) valuation method as shown in Figure 7C in the next Section. Since prices for investment goods and products in inventories are endogenously determined, the current replacement value of NW can be computed from period to period. Ideally, however, a firm’s NW, or equity should be valued at market prices, but this is not possible without a stock market in the model, which today is beyond our ambitions.
Equation (2) however allows us to interpret the objective of the firm to be to achieve maximum possible long term ex ante or maximum long term ex ante real value creation for share owners, even though that ex ante target has no operational meaning beyond the short run (read quarter). The real firm as well as the model firm deals with expectational uncertainty by revising its ex ante calculation from period (quarter) to quarter as unpredictable circumstances change, for instance by revising (each quarter) its P, W and RI expectations and sales, production, recruiting and investment plans. The interesting question of economy wide dynamics is to what extent ex ante short term adaptive expectations (see 2.3 below) over the longer term gear up such that firms’ performance in terms of the short run target satisfaction (Equation 2), becomes rational in the longer term.
In coding the model, great care will be taken to distinguish (Equation 1) between ex ante variables and ex post outcomes, and (Equation 2) – depending on model version- between market values and the corresponding entities taken from the books (accounting values). Since prices change endogenously in model markets, this will be found to be of no minor concern. For wages, se Section 5, and product prices Section 8.
GOAL (see Equations 1–3) can be decomposed into operationally defined components far down into the business organization to which local targets can be attached in internal planning and budgeting that are all consistent with the overall objective function (see further Eliasson, 1976a). Over the longer-term, as mentioned, maximizing ex ante GOAL can be shown to be synonymous to maximizing ex ante firm wealth each period. Since ex ante (expectations, see 2.3. Periodic updating below) rarely come out as expected ex post in the market environment of this model, this should be taken as a theoretically observation in passing.
2.1.2. An additive delegation scheme
Equations (1) and (2) offer a convenient organization /targeting scheme. Equation (1) states that the relative change in firm net worth (DNW) plus the period’s dividend payout (Ɵ) expressed in percent of the same net worth (NW) is the sum of four components.
The profit margin (M) times the ratio between sales and total assets(α), or the short term contribution from production departments (operations management).
Calculated economic depreciation (subtracted) dealt with in the accounting office.
Inflationary and capital gains from asset management. More generally, however, C can be seen as the contribution to firm value creation from managing its portfolio of assets.10 This will be a convenient accounting/control scheme if the model is later extended to allow firms to invest in financial assets in a stock market.
he leverage contribution to the firm’s wealth creation from its finance department defined as the difference between the nominal return to total assets and the (average) interest rate on debt (BW) times the debt net worth ratio (BW/NW).
For the consumer-shareowner the deflator should be the consumer price index (CPI). This is however not an appropriate deflator for the professional stock investor. He is unlikely to regard his wealth as a stored-up consumption potential, at least not with the weighting system normally used to compute CPI. Since the deflator choice has only been introduced to allow an outside assessment of business performance, we need not discuss this matter further. The decision criteria that we will introduce are all invariant vis-a-vis this choice.
Even in small businesses top management is never in full operational control of the internal firm economy. Lack of competence in how things are done, and limited information explains that. Decisions on how to run production must be delegated, and control is exercised through negotiated agreements of statistically defined targets to be achieved. This is clearly reflected in firms’ internal control routines, the budgeting process being the most well-known (Eliasson, 1976a). A theory of firm behavior, or an empirical model of a firm should of course also be explicit about how limited control of its internal affairs affects its behavior. The additive objective profit targeting function (Equation 1) is a perfect empirical algorithm on which to build such a firm delegation scheme, a device that also reflects business practice (Eliasson, 1976a).
Equation (1) tells us that four factors contribute additively to performance in terms of the objective function (1) or (2). Two of these factors are however matched by separate organizational units within firms namely:
Investment-financing (long term) = D
and
operations decision making (short term) = A
(B), or the depreciation factor, is dealt with in the accounting office. Capital gains and losses affect the financial performance of a business and distort the accounts managers use to monitor production operations. In large firms operations management and financial portfolio management are normally organizationally separated (Eliasson, 1976a). Recent experience has however made firm management aware of how inflation distorts their statistical accounts. Maybe the introduction of new inflationary accounting systems in the future will make it possible to organize a separate office for inflationary accounting to manage the contribution of capital gains under C to the overall financial performance of the firm.11
The outcomes of long-term investment financing and operational decision are mutually dependent in a way that will be modelled in detail in the next chapter. The typical feature of firm management, however, is that decisions under A and D are not simultaneous but managed separately. This is one rationale for keeping the long and the short terms separate.
The objective function (1) also gives a rational reason for the concern with profit margins in manufacturing firms (Eliasson, 1976a). If sales-asset ratios are stable over time, M is a monotonous indicator of profitability in terms of those factors that are manageable in the short term. Hence an increase in the profit margin in the short term means an increase in the return to assets. The short term is thus defined to mean the production planning period within which production plans cannot be changed. Profit margins are easy to monitor statistically compared to the unclear concept of a return to capital. For good reasons firms do not use the ambiguous concept of capital in operations planning (see further Section 4 on production planning, and Eliasson, 1976a).
If shareholders value their assets in terms of their purchasing power and their purchasing power is defined in terms of a basket of consumer goods, then their goal variable reads either:
and the real rate of return on net worth{=RRNW-DCP}, or (from 2):
The real (or CPI-deflated) growth rate in net worth, inclusive of what is currently made directly available in the form of dividends.
By breaking M down further as in (3) the separable, additive targeting function (1) can be identified with the internal organizational fabric of the business. In the economy we are for the time being (no purchase of intermediate products and no divisional separation of the firm unit assumed) considering M as composed of three factors:
Labor productivity = Q/L
Wage level = W
Product prices = P.
Prices are typically associated with sales departments while productivity is managed and determined within production departments.
While labor costs can be managed properly at the location where it is applied this is not normally so with prices or profit margins. Since prices and profit margins can be measured reliably only for the end (final) product we have found that firms use a whole range of performance indexes based on W∙L/Q , or unit labor costs, to remotely monitor profit performance at detailed levels of manufacturing production (Eliasson, 1976a).
2.1.3. Feedback MIP targeting
In Equation (1) a CHQ goal (objective) function has been broken down into lower-level operational targets needed for our modelling purposes. Since top managers do not have the knowledge to work out a HOW-plan on their own the budget process is organized as an iterative downward-upward bargaining and exchange of knowledge and solutions to get the numbers right. The final ”solution”, the budget, becomes an agreement on performance to be used as a reference against which to monitor performance and exercise responsibility.12 Such negotiations do not aim for an “analytical solution”, but to force information at operations levels to surface to ensure a realistic performance reference. MIP targeting is part of this management process (see Section 4 on production planning. The MIP targeting process has been documented in detail in Eliasson (1976a). A rational top management constantly strives for long term maximum wealth creation under constantly changing circumstances. This expectations driven planning and decision process controlled by the additive objective and targeting function (1) captures that.
The algebraically based negotiations between top management and operational departments are synonymous with a downward delegation of decisions that is managed from a CHQ that lacks knowledge or understanding of HOW. Hence, top management is concerned with formulating the goals of the organization and breaking them down into operational terms that are understood at lower levels by setting targets on, and enforcing them. Top level targets are used to enforce improvements in lower-level performance without knowing how to attain those targets. The plan or budget finally arrived at becomes an agreement with which ex post performance can be compared and responsibility meted out (Eliasson, 1976a). My ambition is to represent this feedback targeting, negotiation and control process in the firm model.
To solve our problem and still formulate ourselves in empirically relevant terms we introduce the concepts of feedback targeting, whereby the MIP principle is used to apply the right pressure on lower-level management to be up to targets. If this pressure is too tough it is not taken seriously. If it is too soft, lower level management may “cheat” and make top management agree to less demanding and inefficient solutions. Since feasible target performance cannot be calculated without the full cooperation of those who are supposed to do the job, the substitute method is to look at past performance and gently step-up performance requirements without asking for impossible things. The M-criteria in (1) and (3) are therefore based on past experience and set at what can reasonably be achieved in terms of a requirement to Maintain or Improve Profit (MIP) performance. A feedback historical reference target often used in the firms I interviewed is defined in Eliasson (1976a):
On this we apply MIP:
ε ≥ 0, but small
Targets may be enforced more or less. The toughness with which targets are enforced determines how far search for better and better solutions is forced on to the firm organization, especially within the production system (see Section 4). Targets are however normally modified with reference to external (market) information, for instance profit margins achieved by competing firms in the same market niche.13 If a competitor constantly achieves larger profit margins the “inferior” firm knows it can be done and can confidently upgrade its own margin targets accordingly (see equation 6 below, and Eliasson, 1976a).
2.2. Expectations functions (EXP-sector)
Expectations are fix points based on which the firm manipulates its parameters to find a solution that satisfies its profit targets ex ante. Most important for the plans and decisions of model firms are price expectations. Two types of influences on the forming of anticipations are recognized. First, some are generated from internal experience. Such generating algorithms are labelled EXPI. We will apply throughout modified versions of the feedback learning function formulated in Eliasson (1974b). Second, exogenous influences are allowed to enter the forming of expectations of individual firms in various ways. All such exogenous influences are denoted EXPX.
2.2.1. The general expectations generator
I introduce a generalized additive expectations function:
R is the factor that determines the relative importance of internal and outside influences in the forming of expectations.
Example: Suppose Ɵ represents the relative change in the firm’s product price. EXPI then transforms past internal price experience into a future predictor. EXPX in turn transforms externally available price information into a price forecast for the firm. Such external information may be gathered from other variables, official forecasts, the general mood of the market and sentiment in the economy etc.
Long-term expectations are fed into the investment-financing and growth decisions. The long term internal expectations generator is assumed to be adaptive and of a quadratic, feedback learning type:
This formula applies to all expectations variables that we are considering; for the time being prices (P), wages (W), sales (S) and interest rates (RI). Variables are normally defined in relative growth terms. (7) then generates an estimate on the average, annual rate of change for the future period defined as “long-term”. Expected change in Ɵ is a time weighted (declining weights) average of past changes in Ɵ. To this factor is added (1) a fraction of a time-weighted average of past differences between actual and expected changes and (2) a fraction of the same time-weighted differences squared.
λ defines the weighting system. An λ close to zero means a heavy dominance of today in the forming of expectations. The closer λ is to 1, the more important the past.14
α(Ɵ-EXPI(Ɵ)) is a correction factor for systematic mistakes in the past, also weighted in by λ.
β (Ɵ -EXPI(Ɵ))² defines the effect of variations in expectational hits, irrespective of which way mistakes go. A firm may operate in a completely erratic (random) environment to the extent that (Ɵ-EXPI(Ɵ)) averages to ≈ 0 over time, even though some observations may have very large absolute values. If so, the uncertainty involved should suggest caution, since a single, very large negative (Ɵ-EXPI(Ɵ)) could spell disaster for the firm. Hence β should be negative while α should be positive.
Summarizing (Eliasson, 1974b), the expectations algorithm for Ɵ looks as follows:
where
Expectations on Ɵ, called EXP(Ɵ), are adaptive and generated from firms’ own experience as determined by conventional smoothing formulae combined with a quadratic learning function.15 To this can be added the possibility to impose an exogenous adjustment of expectations in individual firms. The profit-targeting function used in the model is similar in form to HIST(Ɵ) above. The possibility of adjusting targets exogenously has also been added here as well as a device used sometimes in formalized profit-targeting systems in U.S. firms, namely, always to raise targets slightly above what has been arrived at in the budgeting process (the maintain or improve principle, MIP, Eliasson, 1976a).
In most experiments the weighting system will be assumed to be identical in all firms. Hence differences in expectations between firms depend solely on a different “variable-experience” and on the coefficients α and β in (7) and R in (6), that may be said to signify the firm’s learning response(=α), the firm’s attitude to uncertainty (=β) and its degree of relying on external information (=R), respectively. In some experiments we will however use the option to characterize firms (real and synthetic) by individualizing the (α, β, R) parameters.
Empirical evidence suggests that firms use quite crude transformations of experience of the above kind in their formal planning routines, and therefore, except in very special market environmemnts, must be prone to constantly making mistakes, in that ex ante plans differ signficantly and systematically from ex post outcomes. As Day et al. (1974) propose, myopic firms, using rules of thumb will be fumbling their their way into the future, a theme that comes back in Winter's (1975) Darwinian theorizing about firm behavior. In practice, therefore, a model can be made quite realistic in this respect. For experimental purposes it will always be of interest to ask how the economy at large behaves under different behavioral specifications among firms. And the model will allow quite sophisticated expectations, moods, and sentiments to be experimented with. Since we believe expectations to be an important factor in the economy, we will allow for the possibility of entering quite complex devices already at this stage.
2.2.2. A cyclical modifier
We know, furthermore, that executive decision makers are frequently subjected to information generated as in (1) and (2) or apply the same kind of calculation themselves, intuitively. Hence modifications related to the short run should most appropriately be entered as a separate short-term or cyclical modifier of long-term expectations (see Eliasson, 1974a). This is done by applying a cyclical modifier to the internal expectations function EXP(Ɵ) in (7).
CYCLE is a transformation function that spreads EXPI unevenly over a future period. It can be a simple sinus function or a more complex cyclical function that is continuously updated during a simulation. Equation (9)) is not yet in the model program.
2.2.3. Sales expectations (EXP S)
Sales expectations, or sales forecasts, deserve special mention since we have modelled business practice to be to project expected market growth, assess the firm position in terms of its market share, project a preliminary sales plan and then try it out step by step. The sales forecast therefore defines the fist step (initiation) of the production planning sequence of Section 4, for which expected profits are calculated and compared with calculated profit targets.
Firms are assumed to begin their sales forecasting by a market price expectation based on EXPP. The total market is called MARK and each firm applies (7) to obtain a preliminary appreciation of market growth EXPIDMARK, assumed to be consistent with EXPP. This “harmonic” assumption presumes no strategic market maneuvers by the firm and no expected strategic maneuvers on the part of competing firms. In other words, if the firm enters the market with its offering price EXPP it also expects to maintain its previous market share ES and:
Later, we will try to build more fun into the model by introducing a tradeoff between offering prices EXPP and market shares ES. In doing so we must establish a link over time between long-term planning and short-term operational planning.
2.3. Periodic updating
Expectations tie in with the annual budget procedure. Operations planning in the model is on a shorter time basis, for the time being by quarter. Experience during the year, hence, is allowed to affect e.g., production planning through updated expectations. This is in line with business practice.
Updating implies a gradual relaxing of annual expectations if disproved by experience. The firm enters the first quarter expecting one quarter of the expected annual change to be realized (no season assumed). For the three consecutive quarters this simple expectation is modified by:
Thus, the realized quarterly deviation from expectations corrects next quarter initial expectation with a factor Ѱ. Obviously the within-year quarterly, adaptive expectations formula (Equation 10) is analogous to the between-year expectations formula (Equation 7).
3. Investment-financing - the long-range planning decision (sophisticated version, not yet in model code)
A useful way to delimit the concept of a firm is to view it as a financial system defined by its balance sheet and its profit and loss statement and governed top down by Corporate Headquarter (CHQ), that within its business plan integrates product, labor and financial market price expectations to satisfy long term profit objectives Eliasson (1976a). The entity so delimited tends to coincide with something that is usually larger than the judicially defined firm. In modelling such a firm we must understand the decisions that regulate its in- and outflows of funds. Such complex decisions are normally organized by delegation under the constraint of a master plan. One property of most decision systems, hence, is that sub-decisions as a rule are inconsistent when pieced together and based on different assumptions and information. The additive profit targeting formula of the previous section defines one such master business plan.
One typical management delegation line runs between the long run and the short run and separates operational production management, concerned with M in (1) in the previous section, from decisions on investment and financing. In firms this demarcation line is very clear both in terms of organizational separation and methods of handling problems. In fact, the investment financing problem represents the typical CHQ function while production decisions are delegated to operational departments and not integrated sideways and upwards. The business plan in the firm model will have this typical feature built into it.
We have already decomposed the master CHQ objective function (1) in the previous chapter to match various organizational subdepartments. One such department oversees the long-term financing function vested with CHQ and is responsible for securing a sufficient and stable flow of long-term finance. This concerns the allocation of resources over time. CHQ is also concerned with the horizontal allocation of resources to its different production lines or to financial investments. Since we are for the time being only concerned with a one product line firm, allocation is mainly over time.16 The investment financing module includes both asset management under C and the short-term commercial banking function, or D in (1) in the previous section, concerned with short-term borrowing and investment activities (cash management).
Hence the investment financing block is built around the following four functional modules:
I. Long term - 5 years:
Long-term profit target and growth plan generates 5-year external financing requirements (balance sheet and profitability criteria).
II. One year, long-term borrowing decision:
Long-term financing requirements from I, plus liquidity assessment and credit market appraisal as manifest in next year long-term financing decision (final).
III. Investment decision and cash management:
(Quarter to quarter)
IV. Realization phase:
The firm enters each period (quarter) with a financial budget for investment. This budget frame is compared with the proposed investment plan, and a compromise solution follows. Excess liquidity is then invested at the short-term deposit rate and needed short-term borrowing is assumed to be available at the going interest rate.
II defines the actual liquidity position of the firm, and it may appear surprising that the only leverage that the long term has on ex post behavior (in the model) operates through this liquidity constraint. In fact, this specification corresponds well with the typical practice of leaving all investment decisions pending or subject to revision until the so-called appropriations procedure, which is normally a quarterly or even more frequent affair. This specification corresponds well with typical firm practice of keeping as many hands free as possible (cf. investment plan realization functions in Eliasson, 1976a).
This entire investment financing module has been set up within an accounting framework model imitating CHQ planning practices as observed in Eliasson (1976a). We have not yet modelled how long term foresight affects R&D spending or the choice of investment projects. CHQ screens proposed projects or project groups from operating divisions within a corporate budgeting financial frame. It does not initiate projects or make technical choices. Neither have we modelled the irreversible financial commitments associated with large investment projects that cannot be stopped once started. This is a misspecification. However, for normal analysis at the macro level this will be of marginal importance since revisions in plans will seldom will be larger than allowed by such bindings. In fact, when dramatic events take place even large ventures in progress are terminated.
3.1. Long term plans
An initial sales projection is entered from the expectations block. After application of simple sales-asset relationships a first preliminary investment plan is obtained. This plan is fed through the production system. Assuming normal, operating (capacity utilization) rates, profit margins can be calculated and checked against targets. This procedure is somewhat backward compared to actual practice since investment plans, or rather requests, are normally prepared by operating departments based on sales plans. (It is quite possible to generate investment requirements directly out of the production system the way it is done, but considering the complexity of the production and investment financing system it would be technically awkward and hardly rewarding. We choose not to do so for the time being, and the two approaches quite conceivably should give approximately the same results).
If M-targets are not satisfied, sales plans are reduced until satisfaction is reached. Dividends to be paid out next year are now decided on. Next follows a balance sheet check.
Maximum debt leverage on the balance sheet is currently calculated along the lines of a Donaldson (1961) type earnings coverage criterion. Financial risks are assumed to be proportional to expected, excess cash outflows divided by net worth, properly valued in current prices (Called NW).17 Maximum leverage is then assumed to be a (linear) function of the nominal rate of return minus interest cost and calculated risk. We thus arrive at the MAX factor (A8) derived in Appendix C. Borrowing associated with the long-term growth plan derived earlier is now checked against the consequences for financial risks, or the gearing ratio Ѱ = BW/NW using the MAX Ѱ criterion (See 4.3 in Appendix B). Borrowing and sales growth are reduced (if necessary) until a state of satisfaction is attained. We now have a long-term plan, and total external finance needed to clear the long-term growth plan (see 17 in Appendix B).
3.2. The one-year, long-term borrowing decision
How much of the external funds for the next long-term period (from now to H) to be borrowed next year depends on the current difference between the long-term and the short-term borrowing rate. (Note that the profit side of the long-term growth plan has already been checked and cleared in the previous step.) If this formula gives less long-term borrowing next year than the needed total for the year, the difference is made up for by short-term borrowing up to planned requirements.
External funds now acquired (11.1 in Appendix B) are added to liquidity (=LIQ. For the time being we simply spread the new cash evenly over the year.
There is one exception to this straightforward procedure that has not yet been modelled. It involves an interface with targeting (annual targeting, quarterly targeting, or even quarterly target enforcement. See 15 in Appendix B). Since this block already has got two full search processes there is no need at this stage to add this third complication. In fact, there will be a device that allows us to shut off one, two or all three complications in experiments when they are not considered important.
The added device (15) in Appendix B is a target modifier that allows firm management some flexibility. First, a deliberate internal, cyclical stabilizing of production is allowed for, through production for inventories, the hoarding of labor and a contracyclical timing of investments. This means absorbing more of the cyclical variation internally by accepting larger cyclical swings in profits. A higher average (long-term) profit level should be an expected consequence and the liquidity position plays a crucial role in the financial capacity to take on larger short-term risks. Second, unforeseen events or strong cyclical swings in profits do not mean that average “feedback” profit targets should be rigidly maintained each quarter. Here again the size of the liquidity buffer can be substituted for a deliberate cyclical timing of targets).
3.3. The investment decision
The first step in the investment decision is to determine the investment budget constraint which is contingent on expected cash inflows less outflows and the allowed change in LIQ. At this level corporate income taxes become important since they influence both internal cash flows and the profitability of investment, as well as the relative profitability of investing in physical capital and financial assets.18
Second, current capital spending categories are regarded as mandatory investment both in the plan and in the actual realization of plans. To sell, firms must follow market practice in trade credit extensions. Hence CHK2(OTHER) in Figure 7C depends directly on CHS. Liquidity (LIQ) is a prime concern in financial risk management and provision for a LIQ buffer takes priority over investment. The same holds for purchasing and intermediate stock building needed to keep production and sales going. A problem arises if we want to introduce speculative stock accumulation and decumulation of raw material and intermediate goods inventories (Section 8).19 We consider it realistic to assume that expected capital gains may at times be sufficiently large to make it profitable to allow such stock building to take priority over INV. Hence the calculated investment budget constraint (INVF in 17.1 in Suppl) must be reduced by the cash requirements from such extra stock accumulation.
Third (17.2), next period (quarter) planned or desired investment spending from the long-range plan is entered. The smallest of planned investment and the revised budget frame constitutes the final investment decision for the period.20 This is a final decision and QINV so determined enters capital goods markets next period (quarter) as final demand.
With the specifications now entered in the investment financing block we have made the size of the firm entity dependent upon its internal generation of cash flows (read profitability) and its willingness to take on new external funds. This willingness in turn depends on expected long-term profitability over and above the cost for external finance (the rate of interest) after consideration of taxes and financial risks. Long term expected profitability in turn, again, depends on the expected productivity properties of new investment and how more productive machines combine with existing production capital installations (Next Section).
Short-term disturbances (mistaken and revised expectations) affect the rate at which the growth plan is realized.
There is always the possibility that returns to pure financial investments may be so high as to make it more profitable for the firm to invest its internal cash flow in financial assets, or as the model is currently formulated at the interest rate offered by the bank. This alternative is only allowed in the model - as it is now specified - as a reduction in its propensity to borrow long-term (which may become negative), and indirectly in so far as a bad profit performance may mean a deteriorating cash position and a need to keep more liquidity invested short-term in the bank.
We have not yet tried to model the typical feature of large business firms to transform themselves gradually into investment companies and commercial banks as well as being master planners of several production and distribution units (Eliasson, 1976a). Modelling the firm as a CHQ portfolio manager of several divisions, and even integrated supporting businesses, is therefore a further possibility.
One would perhaps like to see the choice between internal plowbacks of profits and investing them in the credit market at higher returns explicit in the model. I suggest, however, that we leave that alternative for the time being. To make sense such an extension will have to await a more detailed modelling of the (Swedish) corporate income system. A reduction in internal profitability requirements (compared with direct financial investments) is, for instance, associated with large tax wedges, in some industrial economies due to the tax leakage that occurs when funds are distributed as dividends. Furthermore, fiscal depreciation allowances that are faster than economically motivated exercise the same cash containing influence on firm management as well as stock owners, who prefer to get their money back as capital gains (from successful investments) in share prices that are taxed at a lower total rate than dividends. This will however easily become an illusion if the accumulated interest free tax credit makes firm management less disciplined in assessing the profitability of their investments.
3.4. Updating of balance sheet
Note that α and β may vary over time. Since all Figures 7 are updated each quarter, past period α and β can always be recalculated and used for next period projections. This seems to be a practice often followed in firm internal planning although at a much more detailed level (Eliasson, 1976a).
STO = volume of inventories(See Sections 6:2 and 3)
STOV = value of inventories (=STO ∙ price index)
F = finished goods
z = all intermediate goods {purchases)
Cf. Section 8, and note the variation in nomenclature.
(Cash flow identity. Same as 9.)
The firm model, as well as all planning systems I have studied in Eliasson (1976a) have no explicit production capital stock variable. Neoclassical capital stock variables are considered without operational content, and thus avoided. Since firms construct balance sheets an implicit capital stock measure “is of course there”, and can be indirectly derived. When the balance sheet is updated
INVEFF is the ratio of sales (S) to measured production capital in the balance sheet (K1). When corrected for inflation INVEFF becomes a “capital productivity” measure associated with new investments that affects the production possibilities frontier QFR(L) in Figure 8. See further on the updating of QFR(L) in section 4.2 in the model and on how it is done in real firm planning practices.
Shifting of production possibilities curve because of depreciation and new investments in best practice technologies.
4. Production planning and labour demand
This model block describes the firm production system and the choice sequences that finally lead to a preliminary production plan and a labor recruitment plan. The production system of the firm can be fully described by four sets of data:
A function determining maximum possible output each period for each level of employment, the “production possibility frontier”.
A function that determines how this frontier shifts in response to investment.
A set of positional measures of the distance between actual production and maximum possible production (position).
A description of HOW the firm approaches or retreats from the production possibility frontier from below each period (Search).
The production possibility frontier QFR(L) is described by (1) above as a function of labor input.
Analytically the production frontier is very similar to a conventional production function, except that we do not allow aggregate capital stock volume or a corresponding capital services measure to enter explicitly. Rather, a vector of performance coefficients has been substituted for capital. Together with the level of output, called Q, this vector determines productivity for each period. The distance between actual production and what is technically feasible under various conditions, is determined endogenously in the model. We call this “search for profit target satisfaction” within the production system. This search makes firm productivity endogenous. It is technically rather involved and is specified formally in the Pseudo Code (Eliasson et al., 1976), and graphically and verbally below.
The production possibility frontier is gradually shifted outwards from period to period due to investment spending (see Figure 9). Investment plans of firms are made up each year and determined in the long-term investment financing Section 2 above. The rate of realization of investment plans is determined from quarter to quarter and dependent on current financial market conditions as is also explained in the previous Section. New investment is characterized by higher potential productivity performance rates (called MTEC) than average potential productivity (TEC). New investment affects (potential) productivity in proportion to new potential capacity added, net of depreciation.
MTEC, or “best practice technology”, is exogenous and is acquired from a global technology pool by firms through their endogenous investments. The shifting of the production possibility frontier each quarter is graphically illustrated in Figure 8.
It is partly a semantic, partly a real question whether technological change in the model is “disembodied” or “embodied”. The breaking in of a production system (read a factory) is usually a long winding affair. Productivity growth is thus postponed by the creation of slack that is later activated (see below). We also know that strategic investments or reorganizations (not necessarily involving the spending of large amounts of money) often boost overall productivity and appear in econometric studies as exogenous shifts in production functions. The model - as it stands - is not capable of telling how this takes place. New technologies are mixed with old and stirred well. The outcome is a shift in the average (Q, L) curve called QFR(L) as shown in the diagrams. We plan later to introduce a distinction between capacity augmenting and productivity augmenting investments.
Two resource utilization rates are introduced; one that measures the potential increase in production due to an increase in the utilization of unused but “employed” labor (step 1 to 2 in Figure 9) and one that measures the extent of unused equipment capacity on top of unused labor by a conventional definition (step 2' to 3'). The two utilization rates added (the distance 1' to 3') correspond to a conventional rate of (equipment) capacity utilization measure, expressed, however, in terms of added output. To operate the model, positional start up data on these utilization rates are needed. Such data for the 250 largest Swedish firms were collected for the first time in the 1975 Planning Survey of the Federation of Swedish Industries. During simulations the utilization rates are endogenously determined and updated from quarter to quarter by changing production plans (search) and investment as described in Figures 10 and 11.
An extra feature has been added to the production system, namely the possibility to activate “structural” or “reserve slack” (read productivity) called RES in diagrams, when management pressure is exercised. This occurs when firms have difficulties in satisfying their profit targets. A necessary complement to this feature is to explain how such reserve slack accumulates within the firm. This accumulation is part of the investment process in so far as that we assume that part of the productivity potential of a new investment is not made full use of. “Wasted” productivity is potentially there in the form of a reserve, but up to a limit, above which it becomes true waste. Model firms that have been successful for a long time and never have been forced to resort to slack activation, hence, tend to accumulate slack in the production system and waste potential productivity. On the other hand, competitive pressure and frequent target non-satisfaction tend to keep this waste at a minimum and RES below the maximum allowed. This, however, does not necessarily have to be a healthy thing in the long run, since investment spending may be affected negatively. Thus, as the model economy progresses through time a continuous balancing takes place of the benefits from competition in terms of “static productivity increases”, and the benefits of profitability of investments in long term growth. A rational explanation for the presence of various forms of slack within (firm) organizations assumed in some theorizing during the last two decades (Cyert and Marc, 1963;Leibenstein, 1966, and others). has therefore been built into the MOSES firm model as an endogenous and explainable phenomenon. This codifies the principle that when organizations are having an easy time the efficiency in utilization of resources gradually decreases, and vice versa when the firm is experiencing difficulties.
Both resource utilization rates are what we call slack variables that are activated according to a predetermined sequence as firms increase levels of production each period. Unused labor capacity is first activated. Further increases require the hiring of additional labor to man unused equipment capacity. Additional increases in output in the short run (each quarter) mean crowding of production facilities and/or putting relatively low performance equipment into production and, hence, lower returns in terms of output. How such search for profit target satisfaction occurs in individual firm modules is illustrated in (Figures 8–12), and in full detail in the pseudo code.
4.1. Production possibility frontier
Somewhat simplified the production function or production frontier (QFR) has the following specification (see Figure 2 in Section 1):
This is the static (each period) (Q, L) relationship. No capital stock measure is needed. Investment affects the output potential through updating of QTOP and (see below). QTOP represents maximum possible output at the application of infinite labor, and the activation of the entire slack potential called RES.
As observed in Section 1 the model features no explicit production capital. Such measures, because of their imprecise characterization, do not figure in firms’ operations planning (Eliasson, 1976a, and hence has no place in a model of firm behavior that has been designed to represent firms’ actual decision making.21 Since we have “operational” data on firms' capacity utilization (from the Planning Survey at the Federation of Swedish Industries) the production frontier can be estimated for the initial period simulations are started, and then how that same frontier shifts outwards as firms invest, as I will now show. Firms are found to be constantly located well below that production frontier.
The functional form of QFR (shown in Figure 9) has the standard mathematical property of declining marginal output when expanding labor input along the curve. Furthermore:
and:
we have:
and (1-RES) ∙TEC measures labor productivity of the last piece of equipment to go out of business as the firm reduces operations along QFR.
Expansion of output along QFR, on the other hand, yields a declining marginal contribution for each additional input of labor and, hence, a declining average productivity QFR/L. This gives the desirable convexity to the production system. Performance (productivity, profit margins) improve as workers are laid off and better and better equipment (on the average) is used.
Equipment is updated by investment (see Section 4.2) from the origin. The specification of QFR(L), hence, embodies both technology (productivity) vintages and the order by which these vintages are activated in and combined with L or taken out of production. Consequently, the decreasing marginal output of adding more workers (L) to existing production equipment (we call it “crowding”) is automatically taken care of. Since we feel no need to study or explain how this combination takes place, we can use this very convenient formulation.
Each period, each firm is described by its QFR(L) and its current operating status somewhere inside QFR(L), say, point 1 in Figure 9). The vertical distance 1 to 2 measures redundant labor in terms of the potential increase in output the firm is capable of without adding to its labor force. The vertical distance 2 to 3 (to QTOP∙(l-RES)) measures the maximum extra increase in output that the firm is capable of by hiring additional workers but (NB!) without activating any slack. QTOP (l-RES) is of course out of reach, being the asymptote towards which QFR converges when more L is applied. Distance 1 to 3 along the vertical scale can be said to define unused equipment capacity.
Estimates on 1 to 2 and 2 to 3' are collected from 1975 on individual firms within the annual Planning Surveys of the Federation of Swedish Industries. In fact, this research project has had the opportunity to formulate the questions asked and the response rate has been surprisingly high considering the complexity of the questions.22 The reason for the high response rate most probably is that questions have been phrased on a format that corresponds to the statistical taxonomies and planning routines within firms as studied in Eliasson (1976a).
The question relating to the distance 1 to 2 is quite straight forward and need not be commented on, except perhaps that the questioning technique is new and the assessment of the quality of data will have to await further experience. To measure the distance from 2 to 3' is more complicated since QTOP (l-RES) is outside the potential economical operating range of the firm. Instead, firms have been asked to estimate maximum economic output under favorable business cycle conditions, say point 3'. Let us assume that they tell us the point where the expected marginal value product equals the expected wage. We will not know and there is no need to. That however is where:
Note that if we believe in our EXP’s as representative for firm EXP’s this equation should hold if marginal conditions hold. The derivative is immediately available since we have QFR specified. Hence, the operating rate estimates we obtain for positioning of firms are 1' to 2' (= 1 to 2) and 2' to 3' along the vertical scale. We will call them A21 and A22 respectively.
Besides the positioning of firms below their QFR, these data (NB!) also provide what is needed to approximate the numerical form of QFR(L).
Since point 3' on the vertical axis is assumed to approximate (1-RES) QTOP in (1),23 and since (QFR(L), L) in 2 is known from the survey, (1) can be solved numerically for . Knowledge of L in 3' can then be used to check whether firms have delivered consistent data.24 I see no way of obtaining an estimate on RES (and hence QTOP) except by a priori assumption.25
The idea behind the reserve slack concept RES is that firms do not know themselves about its exact magnitude. CHQ applies top-down pressure when targets are not satisfied. CHQ knows that the reserve is there. Lower-level management who knows HOW are forced to activate it. From this position, which is empirically sound (see Eliasson, 1976a), we should not attempt any further direct measurement by questioning firms on RES for the very reason that they cannot provide better information.
4.2. Updating QFR(L)
Updating of potential output change by a firm can be separated into two sets of instructions: updating of (1) QFR(L) and (2) the positional characterization (initial state) of the firm below QFR(L). Both take place each period (quarter).
Since capital stock is not explicit, the parameters regulating production are updated instead by investment (INV). Firms do not use measures on physical capital stocks in their internal accounting and planning routines,26 and for good reasons. Such measures have no operational content. INV is endogenously determined as described in the Investment-Financing section in Section 3. As new investment originates there each quarter it affects TEC, QTOP and RES. At the same time (or rather before) old equipment is depreciated by writing off potential output in a fashion that preserves the vintage and ordering combination described earlier.
First, the old output capacity is written off at the rate RHO which (ceteris paribus and no new INV) bends the QFR(L) curve in Figure 9 downwards. Second, new INV enters with a new and superior productivity specification MTEC that is exogenously determined. Through their endogenous investments firms tap into an exogenous (“international”) pool of “best practice” technologies, assumed to be more productive than the best investment vintages already installed. The current investment value INV is transformed into current output value by the ratio between value added and replacement valued production capital (K1). This ratio is updated in INV-FIN section (in Section 3). This is the current procedure in firm planning routines. It allows us to avoid the difficult concept of a capital stock in the “production function”. The transformation ratio is called INVEFF (see 11 in previous Section). The replacement value of production equipment can therefore be calculated, however, not the volume of capital stock, which is the concept we want to avoid.
The estimation of INVEFF is, however, problematic. For the time being we simply estimate the average ratio from balance sheet data and update the ratio from period to period. The nice thing, however, is that time will provide us with a more satisfactory set of data that links investment spending directly to the “production function”. From the annual planning Surveys of the Federation of Swedish Industries we will get a time series of the utilization rates A21 and A22 and investment spending INV for individual firms. This should allow us to estimate the relationships between INV and QTOP and shifts in QFR(L) directly.
(A fraction (called LOSS) of the new output potential added by investment is immediately transferred to the reserve slack (RES) potential that accumulates up to a maximum value (RESMAX). Beyond RESMAX the LOSS fraction becomes “waste”. This determines how the shift in QTOP and MTEC boosts TEC in proportion to a new QTOP).27
As for the change in position of the firm when passing the period line, two things must be accounted for. There is an automatic retirement rate which means a reduction in L i.e., less redundant labor and/or a movement along QFR towards origin. As described in the next chapter the new delay lay-off rules in Sweden (called the Aman laws) are explicit in the model, and prevent firms from immediately laying off redundant workers.
Period change means a reshuffling in the Aman vector of not yet laid off workers in the sense that redundant workers are either employed back into production or moved closer to being fired (See Section 5.5). Note, however, that outright firing of workers only takes place when profit-targeting requirements are not satisfied (also see Eliasson, 1976b).
Literature offers a menu of devices to specify a production function where aggregate production capital enters explicitly. For two reasons we prefer to avoid the neoclassical aggregate capital in our production function. First, corporate headquarters of firms never control the numerical structure of their production system, but manages it from a distance based on approximate knowledge and management pressure (see Eliasson, 1976a). Since firms do not themselves use aggregate capital in their production planning, they cannot provide us with meaningful data. Second, K in a neoclassical production function is an aggregate that depends on the relative prices of products manufactured. When output composition changes such physical capital aggregates becomes unstable. Since market induced structural change is our main concern, neoclassical production capital becomes a useless concept. There is a reason for capital being a controversial concept in economic theory.
4.3. Search for satisfactory production plan
The firm can now decide on its production plan for the period. All expected product market prices, wages and the interest rate will be integrated in a profit- target satisfactory production plan. First firms transform their sales expectations from the EXP section into a preliminary production plan by adding or subtracting a desired change in inventories:
This provisional production plan equals the expected sales volume plus a fraction (TMSTO) of the difference between optimum and actual inventory volumes. TMSTO = 1 means that firms plan to close this gap each period.28
A complicated search now begins within the production system that is repeated each period (quarter) for each firm. The production system has a specification which means that the firm will follow a particular search sequence that is determined by (1) expectations (2) initial position below QFR(L) and (3) the numerical specification of QFR(L) and TARGM. Search takes place along “segments” that are either curved or linear.
Two devices will be used; one economic called SAT that terminates search and one technical SOLVE that determines the new position of the firm at a (Q, L) point, where the profit target is satisfied. At a target satisfaction (SAT)point the following should hold:
and the L-point is obtained by inverting (22):
Search will normally be terminated within one “segment” or “path”, and not in a corner. Therefore, we need SOLVE.29
SAT is a criterion that determines when profit targets (TARG M, see Section 2) have been satisfied. This search procedure is run for each firm each period (quarter).
4.3.1. Expansion through activating redundant workers
The initial sales estimate for the next period may not require the hiring of additional workers. A steady “natural” retirement means an automatic decrease in employment. Cost calculations based on expected wages and prices may, however, show that profit targets are not satisfied. The firm knows by experience that production and sales can always be increased somewhat to improve profits. This is the rational first step if there are excess product inventories available. Hence the firm increases production no more than:
Expansion stops as soon as target satisfaction is reached (if it is) along the path A to B in Figure 10 (A is the initial position). If SAT is not attained, then a lower employment level is checked until SAT within the limits prescribed by the AMAN Laws, and path B to C in Figure 10. (See further next section 5.) If target satisfaction is not attained the firm begins to lower both production and labor along path CD on the production possibility frontier. When target SAT is reached the corresponding production plan can be solved for.30
If target SAT has not been attained when SEARCH is down at D below the initial production level at A middle management begins to sense the first signs of crisis. Normal operating practice does not help to solve the profit problem. Plans to reorganize production, shut down some activities, get rid of redundant staff etc. are activated from top down and the fraction of the slack reserve (RES), that can be activated at short notice is used, meaning that productivity can be improved by getting rid of people without lowering the level of production (path D to E).31 Slack activation stops as soon as targets are satisfied.
If, after the immediate productivity reserve has been used, SAT is still not attained firm management recognizes a crisis and begins to discontinue production lines and contract operations along [(1 + RESDOWN)/(1- RES)]∙QFR) from E towards the origin. The convexity of the production possibility curve should normally guarantee a solution with target satisfaction before zero, and with some production lines active.
Again, note here that labor market laws represented by the AMAN vector (as long as they are called in) are always obeyed until just before the origin, or bankruptcy. Furthermore, the strength by which search is pushed all the way through ABCDE and finally to the origin depends on (1) the toughness of profit targets and (2) on top management’s willingness to relax targets temporarily. For the time being we do not have the possibility to relax targets in the program, although the principles for temporary target relaxation have been discussed in the investment financing chapter. We expect this willingness to depend on the current financial situation, although we know that attitudes on this point differ substantially between firms.32 Preliminary experimentation with the model has demonstrated that the firmness with which this target device is exercised is imperative for the behavior of the entire economic system. This is a desired property, since the use of targets of the kind specified in the firm model is quite well documented (Eliasson, 1976a).
4.3.2. Expansion beyond present pool of workers
If initial sales expectations are expansive to the extent that additional workers must be recruited, we are at a point A on QFR somewhere beyond B in Figure 11. The first step is to check whether this is an overoptimistic expectation in terms of profits. If OK this is the plan. If not, convexity of QFR and the margin requirement requires a move left towards B.33 If profit satisfaction is reached before B this is the plan. If not, the whole thing was a mistake, and we begin discarding redundant cost items. Since we are already on QFR and have tried the data there the next step is activation of slack from B to C and then - if this does not help - contraction begins from C down along the production frontier towards the origin in Figure 11.
The difference between search activated from two different expectational positions illustrates the importance of the hierarchical ordering of decisions. Here numerical specification of the entire production system is identical in the two cases. However, differences in initial position and attitudes start different search sequences that follow different paths and yield different results. In this case expansionary initial plans mean that the firm may pass over less beneficial stopping points below QFR. The question posed is both operational and testable, and it is probably - lacking the empirical information for the time being - quite sound.
Expansionary expectations can be expected in rapidly expanding firms. This property is already embedded in our expectations functions. Also, targets are based on past performance. If satisfaction is not reached on path AB in Figure 11 there is no reason for firm management to search for an even less satisfactory solution below QFR. Hence, strong expansion in the past breeds expansionary expectations and contributes to better productivity performance by making firm management more aware of the potential, than would otherwise have been the case. It should be noted, though, that setbacks in profit performance through competition or the business cycle may break this attitude. In the model this happens through a gradual (feedback) lowering of expectations and targets.
4.3.3. The preliminary operating plan
Once a SAT point has been found this is also the preliminary operating plan. The steps taken are illustrated in Figure 12. First, normal retirement shifts the initial position of the firm left to a new initial position. Second, when passing the period limit, investment shifts QFR(L) outward. Third, when search has been completed a new production plan PLANQ has been determined. Preliminary labor demand is obtained by solving the inverse of () for L and subtracting the existing labor force:
The firm is now positioned to adjust its labor force to correspond to its production plan. If this adjustment can take place, then
PLAN(CHL) may be negative, and workers are “filed” for layoffs in the AMAN vectors defined in Swedish legislation.34 Otherwise, two things can happen that disturb the preliminary plan. The firm may be raided by other firms and lose workers, or it may look for workers (including raiding other firms). This is described in the next section.
5. Labour market search
Firms search for workers and lay off workers in the labor market. Employed workers are recruited if wage offers are sufficiently above their current wage, and from the pool of unemployed if offered a wage on par with unemployment benefits or above. Employed workers learn stochastically about wage offers from other firms. Labor is homogenous, and the productivity of employed individual workers is determined by the productivity of the production equipment of the firm they work for. The spread of wages depends on the intensity of competition for workers, the diversity of firms’ productivities and the state of information about wage offers. The labor market search in principle engages the entire labor force and involves several interactions between employers and workers during each period (quarter). Employment “contracts” are settled whenever a firm and a worker have agreed, that is during quarters. Search each quarter is terminated after a preset number of wage offer rounds. In practice individuals are actively involved in the complicated search process to be described.
The labor market is central in the model. Firms that desire to increase employment are here competing with one another, with the service sector and the Government for a given (exogenous) pool of workers. The labor market is already the most complex part of the model. There are four reasons; first the labor market is an important economy wide resource allocator. Second, the origin of inflation - one theme of the modelling project – may be located there. Third, the labor market offers more modelling opportunities than other markets and behavioral blocks, partly because of the availability of statistical information. Hence, this block has been modelled in a way that gives a broad menu of choices as to further elaborations. Fourth, search processes are real economic phenomena. They require not only involved and intricate chains of program instructions, but also use up a lot of computer time. As computing capacity increases, they can therefore be both theoretically and empirically represented in ways not possible before. This defines a positive future for the microsimulation method and mathematical simulation in social sciences.
Still, the specification now to be presented is what I would like to call an unsophisticated version of what we hope will later be possible. The most important clash with realism is the restriction to homogenous labor and the absence of overtime work. Furthermore, we will not allow any direct interaction between the business sector on the one hand, and the service and Government sectors on the other. The service and Government sectors will be treated as aggregates only. This contrasts with the manufacturing industry, which is detailed down to within the firm unit.
5.1. Labor market search
At the beginning of each quarter all new entries to the labor market are allocated to the pool of unemployed (LU) or rather the pool of jobseekers. New entries are determined exogenously. Demand from the service sector and the Government enters first each quarter and in that order. Finally firms signal their intention to recruit workers at an individual offering wage determined in the business plan in the previous chapter. Before a firm enters the labor market to recruit or lay off workers, normal retirement is subtracted. The same rate of retirement applies to each firm.
While the service sector and the Government are restricted to the pool of unemployed in their choice of workers, manufacturing firms can also raid other firms for workers. Because of the recent fill-in with new entrants to the labor market the unemployment pool is quite large at the beginning of each quarter.
The average wage (and salary) levels as measured in the planning survey differ a lot between firms, partly because of differences in pay for the same job but mainly because of different mixes between skilled and unskilled labor. Hence, if we maintain the homogeneity assumption and work with actual, real-life data, the service sector, for instance, would be unable to recruit people in direct competition with industrial firms, where the average wage is about 20 per cent higher. Similarly, if we allow firms to raid the service and Government sector, those sectors might lose a major share of their labor force during a business upswing. So for the time being the interesting labor market dynamics occurs in the manufacturing industry, and the productivity of manufacturing workers depends on the productivity of the firms’ production system, a specification that has been empirically reasonable for a long time, but increasingly less so in recent years. This specification will therefore have to be attended to in future to allow for different competence and skill levels of workers.
5.2. The service industry
The service industry enters the labor market as an aggregate. A profit target is defined for the sector which is assumed to operate without capital and with an exogenously determined rate of productivity change. This target is aimed at each quarter and the sector discards or hires people each quarter to the extent that the profit target is satisfied based on past quarter wages and prices.
Since output volume is assumed to be proportional to labor input this device also determines the next period service output, if the necessary, desired increase in employment can be obtained from the pool of unemployed.
The wage offers of the service sector each quarter is the change in average manufacturing wages the quarter before.
Preliminary offering prices are raised as much as wage offers less the exogenous labor productivity change. The service sector can only get people from the pool of unemployed and not yet employed workers are assumed to be forthcoming out of this pool to the extent wages offered exceed unemployment benefits. If the pool is not large enough, planned output is curtailed correspondingly. This is a rough and ready specification borrowed from the IUI macro sector model. With data on service firms available, this sector could however “easily” be introduced in micro together with the four manufacturing subindustries. Output, so determined, is offered in the service market. The price level in the service sector, however, is not determined until after the confrontations with consumer demand (see Section 7).
Profits in the service sector are 100 per cent treated as household income in Section 7. The very large profit margin in the service sector is mainly because most businesses in the sector are not incorporated. Hence, the owner’s income appears as profits in official statistics. There is also a sizable capital invested, mainly in the form of inventories of trading companies, that we neglect for the time being.
(To introduce inventories here we will have to split the service sector into one part of intermediary traders between industry and households,35 another part devoted to pure service production directly for households, and a third part devoted to outsourced, ofthen highly knowledge intensive services to manufacturing firms. We consider the above specification appropriate until further extensions of the model in this direction have been completed.)
Our approach to the labor market may be interpreted as a codification of manufacturing industry as the wage leading export industry that sets the limits of wage increases elsewhere, a common view among economists of how wage bargaining is conducted in Sweden,36 and compatible with our specification of allowing the service sector to enter the labor market first, offering the previous quarter’s wage increase in the manufacturing industry.
The production-profit targeting system of the service sector is specified as follows:37
RET = retirement rate m (exogenous)
The offering price is calculated as:
This price makes M equal to TARGM if
planned output A1∙L can be sold at that price and
if CHL can be hired at the wage W∙(1+X), where X is the relative wage change in the manufacturing industry in the period before.
5.3. Government Sector
Government is treated almost identically to the service sector. The principal difference is that output this time is exogenously determined as proportional to the number of government employees, assuming zero productivity change, as is standard NA practice. We may even call government employment a policy parameter. Government output is distributed free of charge. For simplicity, in this early, government is financed by a flat rate tax deducted from all incomes generated in the model.
Government influences the price level indirectly through its demand for workers. We can therefore study the impact on the price level of government service production, or - alternatively - of fiscal policy, by varying government recruiting. Like the service sector the government can only recruit people from the pool of unemployed. It offers the same wage increase as the service sector but comes in second and runs a larger risk of not getting enough people. If it cannot, which is an unlikely situation, government output decided on is simply not realized. Specification of the production system is identical to that in the service industry. Productivity change is exogenously set to be zero, and there are no profits.
5.4. Manufacturing Industry
More sophistication is entered with recruitment by manufacturing firms. Preliminary recruitment plans of each firm were determined in Section 4.3. Firms are now ranked in decreasing order by PLANDL, or by how many workers a firm plans to recruit. Firms start searching the labor market in that order.
Each firm is given a probability of being raided by other firms equal to its employment as a fraction of the total labor force, excluding those now employed by service and Government sectors. The probability of search leading to the unemployment pool is calculated analogously. Each firm has its own expectations as to the next period’s wage, EXPW. Its offering wage is a fraction λ of its expected wage change:
When the period starts each firm adjusts its own wage level to its own offering wage. When the firm searches the unemployment pool, labor is forthcoming at that wage offer up to THETA per cent of the pool each time, provided the wage offers exceed the unemployment benefits.
When the firm raids another firm a matching of wages takes place. If the offered wage is higher than the wage level of the searched firm plus a fraction (GAMMA), then the firm acquires up to THETA percent of the raided firm’s labor force. Thus:
Note that I identifies the active, attacking firm and II the raided party.
The raided firm responds by adjusting its wage level upwards by a fraction of the experienced wage difference to reduce the risk of another, similar experience.
If, instead, the searching firm meets a firm with a higher wage level it obtains no new workers. However, it responds by adjusting its own wage level and offering wage upwards:
This search is repeated NITER times each period. The adjusted L and W numbers reached after NITER attempts are entered as final for the period.
If a firm has lost so much labor that there is no redundant labor, and some more, its preliminary production plan has to be revised downward correspondingly. Ditto for a firm that has not been able to recruit labor according to its plan.
The wage and output change for the period can now be calculated and both figures feed back into the expectations block to update expectations for the next period.
The firm parameter vector {λ, THETA, GAMMA,KSI} should be looked at as important characteristics of the speed or efficiency of labor market intermediation. For the time being these parameters are the same for all firms, but as we gather more individual firm panel data in the planning surveys it will be possible to customize these parameters by firm.
5.5. The AMAN vector
For firms that carry redundant labor (= most firms, most of the time), and that are under target pressure to the extent that they decided in their PRODPLAN (in previous chapter) to lay off people, a separate device applies. To account for the new Swedish labor market legislation (the Aman laws), that lay-offs are allowed only after a 6-month delay, a so called AMAN vector has been entered between the decision to lay-off labor and actual lay-off . Redundant labor is filed there in two quarterly cohorts. People in the second cohort at the end of a period can be fired the next period. The cohorts are filled, emptied, or moved one step forward each period for each firm. Actual firing always awaits the end of labor market search. Then the last cohort is emptied into the pool of unemployed. Note here, that when checking for target SAT in the production system, labor in the AMAN vector is subtracted from total L.38 The economy wide consequences of the introduction of the AMAN law have been studied on this model in Eliasson (1976b).
It should be noted finally that the unemployment pool is identical to the conventional concept of unemployment only at the end of each quarter. This definition in turn is consistent with the specification that the model generates quarterly ex post data.
At the beginning of each quarter the unemployment pool is a variable of considerable magnitude since it has been amplified by new entrants and those being laid off (according to plans) by the service sector.
6. Exports, inventories, and intermediate goods (firm level)
All sevctions, except the previous one, have dealt with the specification of the model of a firm. Before we proceed (in the next two chapters) to allow all firms to be confronted with demand a few additional features of the firm model must be introduced. These are:
an explanation of how much of firm output that is sold abroad (exports)
inventory management, and
the input of raw materials and semi manufactured goods (intermediate products) in production
The last-mentioned mechanism is not yet in the program and must be treated rather crudely for practical (data availability) reasons. All three complementary features might alternatively have been entered in the expectations-production planning chapters.
6.1. Exports
Most of the large manufacturing firms that dominate the group of real firms in the model will export well over 50 per cent of their output. For firms in the raw material subsector the export ratio for most firms is 70 per cent and above.
Exports are said to be the prime mover of the Swedish business cycle. The business plans of the firms of the micro macro model are governed by price signals. Since export prices are exogenous, one of the first questions addressed to the model was under what conditions export price changes will generate a domestic growth cycle of the kind observed during the post-war period; how fast (1) do export price changes generate domestic economic cycles via endogenous changes in firms’ exports, and (2) is the rate of transmission of (exogenous) export prices to endogenous domestic prices.
Exports are part of total (sales) planning of model firms. Firm management considers the economics of total expansion irrespective of where its output finally winds up. Firms allocate deliveries to foreign and domestic markets depending on their relative contribution to the firm’s profits. The export ratio of total sales is therefore explained by relative foreign and domestic price development:
else
This export ”leakage function” makes change in the firms’ export shares dependent upon the relative development of foreign (PFOR) and domestic prices (PDOM) with a delay. Domestic prices are endogenously dependent on firms’ relative supplies of goods in domestic and foreign markets.
assumes labor productivity and wages to be the same in production for export and domestic markets. Hence from (3) in Section 2 the only variable factor in relative returns on export and domestic business is the relative price fetched in each market.39 Relative returns to capital or relative profit margins will then be the guiding variable and we might as well write:
else
(42) can be demonstrated to be approximately equal to (41).40 XR should vary very much in phase in both versions because of the common price signal. (41) is however much simpler to use if the price-variables are readily available. If the difference persists over time both (41) and (42) will tend to move XR either towards 1 or zero. The empirical problem that remains is to assess the rate at which change takes place by determining γ.41
The "export leakage" functions (41) and (42) make the export share of a firm dependent on its relative development of export and domestic prices with a delay. Foreign prices are exogenous, but can also be endogenized if the exchange rate is endogenized. The rationale for the two export rate functions of course is the implicit assumption that labour productivity and wages in production for domestic and foreign markets are the same, implying in turn that production for export is more than a marginal busines for the firm. Even though quite traditional, especially when formulating macro export functions, we therefore have a problem modelling Swedish firms’ export functions, especially when it comes to the large international corporations, the five largest of which deliver one third of their output in domestic markets, one third in foreign markets through their foreign subsidiaries and one third in the form of direct export deliveries from Swedish production units according to a recent study (Eliasson, 1971) from my department at the Federation of Swedish Industries. The Planning Survey, on which the micro to macro model is based, is dominated by the large Swedish multinationals, but only covers their domestic production by division, and hence aggregates direct exports and deliveries to their foreign subsidiaries. While Swedish foreign subsidiaries are largely marketing organizations or engaged in late-stage modification of products for local markets, the international specialization of the production of the large firms is increasing. This fact will therefore soon have to be accounted for in the firm module. Currently data is lacking for such an extension, which is best done when the firm module is extended to integrate the divisions of the Planning Survey into complete corporate entities. Then the effects of organizational change on productivity can be made part of business innovation (see footnote 17). Soon data on the international operations of Swedish firms will also become available from a unique study under way at the IUI (Swedenborg, 1973).
A realistic determination of Swedish exports therefore is more complicated than changing functional form of the export function. Our formulation is OK for a firm that is mainly supported by domestic markets (e.g. a normal U.S. firm), and regards exports as a marginal operation. This is not so for the largest Swedish firms that have invested in developing a local presence in foreign markets. For many Swedish firms Sweden is in fact the marginal market, even though production is still mainly domestic, even though also that is rapidly changing towards international specialization (Eliasson, 1971; Eliasson, 1972a). For some of them equation (42) would perhaps be acceptable since bad margin performance in Sweden compared to elsewhere would tend to increase the export share. For most Swedish firms with export shares ranging between 30 and 70 per cent the problem is different. For them the export market is needed to support overall scale economics and efficiency. It is often rational for such a firm to operate with substantially reduced margins in the smaller markets, or during a long introduction phase, since the additional products corresponding to one market can be produced at very reduced unit costs. For them a large reduction in the export share might mean either a large increase in the domestic market share, or a serious problem. Unfortunately, we cannot model such relevant complexities at the present stage. One empirical requirement that we place on the model is, however, that individual firms generate reasonable export shares over time in simulations. Despite these considerations the simple formulation in equation (42) pinpoints the variables at work on a firm’s export share, and it should be mentioned that we are making it difficult for us by avoiding common short-cuts such as basing export functions directly to an exogenously given foreign market growth rate.
6.2. The inventory system
Many economists believe that the origin of business cycles should be looked for in the inventory cycle, inventories being on the one hand the buffer that picks up the consequences of mistaken expectations and on the other hand a sizable demand component with a series of feedback multiplier effects (Holt et al., 1960; Mass, 1976). One empirical question that we are asking is whether mistaken expectations alone may generate the typical business cycle of an industrialized country without an oscillatory mode being built into the sequence of intermediate inventory systems throughout the economy (raw materials, intermediate production through several stages all the way up to the wholesale and retail sectors and households). Do economic agents react on the red and green lights (“Red light theory”), or on the car immediately ahead (Tailgating theory). We do not know and must try both versions.
For each inventory system (products stored) we will introduce three ratios:
Equation (43) defines the optimum inventory (volume) level in terms of the current sales volume. Firms are assumed to gear production (and purchase) plans so that inventories change in the direction of calculated optimum levels. This mechanism has already been explained for finished goods inventories in Section 4.3. The determination of BETA is important for the cyclical properties of the model economy.
For each inventory type we also introduce a MIN and a MAX level expressed in terms of the optimum level. The three ratios (BETA, SMALL, BIG) are operational concepts. They are normally numerically explicit in firm planning routines. They usually vary somewhat over time although there are firms that use a fixed set of coefficients over long periods in their planning and budgeting routines (Eliasson, 1976a). Determination of these coefficients, however, requires access to internal information within the firm.
MIN is the level below which management (under normal conditions) will not allow inventories to go. Similarly, MAX defines the upper limit. For convenience we will regard MAX as maximum storage capacity disregarding the fact that our definition then requires BIG to vary, since sales volume normally varies more over time than warehouse capacity.
To specify the inventory system numerically (and eventually we will deal with at least two inventory components; finished and intermediate goods) two methods are possible. We can measure actual inventory-sales ratios for all firms in a market and/or for individual firms and assign the ratios by some ad hoc method. This will probably do quite well for the kind of macro analyses we have in mind.
The second and more appealing method would be to directly question firms (in the Planning Survey) on their (BETA, SMALL, BIG) ratios and their current STO-sales volume ratio (to measure the degree of startup disequilibrium) and then to assume fixed coefficients in simulations.
6.3. Intermediate products and stocks (not yet in program code)
Each firm is associated with a market for finished products. Each firm also has a purchase pattern related to all other markets. And purchasing is an important and often centralized activity in large manufacturing firms (Eliasson, 1976a). Still, it has not been possible to obtain statistics on this purchase pattern for each firm in the Planning Survey. Internal accounting routines in firms are devised such that separate, very extensive statistical inquiries are needed for CHQ itself to obtain this information. Data on total purchases are however collected. Our solution is to “aggregate up” the Swedish Input Output matrix as close as possible to obtain data on the market segmentation that we use for the model, and then apply the average input delivery pattern of each cell (= market) to each firm classified on that market. With a large number of firms in each market individual errors originating in this deliberate misspecification should tend to cancel.
In principle, each physical output unit (Q) requires an input (volume) of raw materials and intermediate goods. We assume these individual firm input output coefficients to be constant over time. The volume-to-volume input-output coefficients will be estimated by relating purchases to value added, both expressed in current prices.
A point estimate for one year is normally distorted by inventory movements, so hopefully some average over several years can be obtained. From then on, we will allow the input-output coefficients, expressed in current prices, to vary in response to variations in relative input-output prices even though the “physical” coefficient is assumed to be fixed.
We know that the production plan for the year PLANQ consumes:
IMQ(I) stands for physical units of output from market I.
This will cost the firm an expected:
for the same period.
Each firm has stocks of such intermediate input goods. For each type of goods, we define a MAX, an OPT, and a MIN relationship to the level of sales as in the previous section. Stability of production requires that stocks be kept above MIN levels. MAX levels are determined as before as maximum physical storage capacity.42
The firm purchase decision involves (for each purchase category) an estimate on the current use (consumption) of such goods for the period and a decision as to where between MIN and MAX to adjust stocks. This last decision relates directly to the expected price gain on advance buying and vice versa.
Each firm applies a price expectations function of the conventional smoothing type for each purchase market. We expect the experience of the immediate past to dominate in the formation of expectations for the immediate future (one year or one quarter).
The purchasing decision is reconsidered each quarter based on what firm management expects price change to be over the next, say, year. Hence, we define EXPDP(I) to represent the expected price change over the next 4 quarters and EXPP(I) the price at the end of these 4 quarters. P(I), the price of the current quarter (0) and EXPDP(I) are sufficient to determine EXPP(I) end of quarter 4.
The purchasing decision is taken early in the sequence of planning steps described in earlier blocks, and before the preliminary production plan has been arrived at.
Additional storage capacity and planned use over a future 4 quarter period define the scope for inventory buildup in response to expected price increases. Planned use is calculated based on planned sales volume for the long-term plan (first year). This estimate of planned use for a 4-quarter period is then rolled on each quarter. The only component that changes is the difference between MAXSTO and actual STO.
(If EXPDP =0 we now assume:
QIMQ(I): =SPEC∙((planned use) + MAXSTO(I)- STO(I))
planned use: =
where IO is the appropriate market input output
(the upper limit must be enforced)
PLANS is first year in long-term sales expectations from EXP block.
Note that the decision to purchase IMQ(I) refers to the next quarter 1.
If EXPDP < 0 we assume instead:
QIMQ(I):= SPEC2∙((planned use) - STO(I) + MINST(I))
SPEC2 = SPEC22∙EXPDP(I)
Lower limit:
Upper limit:
Maximum financing allocated from investment financing block (if lower than lower limit, some other financing requirement has to yield).43
If within lower and upper bounds we assume that the firm budgets:
for next quarter purchases of Q(I), and immediately proceed to realize the decision.
Firms in market (I) have already made up their production plans. Their supplies in the market are given. I propose the following two alternative market processes. They should both be experimented with:
(I). Domestic supplies and inputs of I are given in physical terms elsewhere in model. Total supply in physical terms and total demand in money terms are added and the clearing price determined. The clearing price is fed back to producers who decide how much they want to keep in inventories. A new volume supply is then obtained, and the clearing prices are recalculated based on an unchanged money demand. That gives the price for the quarter,44 and input goods I are distributed to firms in proportion to their original money budgets (now all spent).
(II). Alternative II is more sophisticated. The first step is as before. When confronted with the new clearing price offer, buyers still want to buy originally planned volumes whatever the new price levels. If foreign prices are lower than this domestic price offer, imports fill in the remainder at this price, preventing the domestic price from going up further this quarter. If foreign prices are relatively higher and/or if the supply volume larger than demanded, alternative I decides.)
As soon as the purchase has been realized inventories are updated:
As soon as the production plan has been finally settled actual use of intermediate goods for the quarter can be calculated by applying IO as above and stocks can be updated again.
The above treatment of purchases refers to two sectors in the model, raw materials and intermediate (including non-durable goods. Demand for investment goods is determined through firms’ investment functions.
7. Household consumption
This demand module interacts with manufacturing firms in a way to be described in the next Section. For reasons of textbook familiarity, I keep the presentation of supply and demand sides of the model separate even though the two sides interact sequentially in product markets both within each period and between periods and in unfamiliar ways.
7.1. Introduction
Household spending and savings as specified in this section relate to one household. For the time being we will however assume that all households are identical (“representative”) and atomic. Hence, we are in practice presenting a macro household module. As things currently stand, we have prepared for a transfer into micro specification of heterogenous households of different sizes and wealth endowments, but lack of empirical data rather than formal and technical problems explains why this has not been done yet.
Consumption of one household follows a priority ordering by a set of spending categories along the lines modelled by Stone (1954), and Klevmarken and Dahlman (1971) and others in so called linear expenditure systems. Novel features introduced here are: (1) personal saving as a separate “future consumption” category.(This means that the “budget constraint” is defined as disposable income (DI) rather than total consumption): (2) a swap between saving and purchases of consumer durables. The idea of the latter is that purchases of durables include an element of saving. Total household wealth is the sum of financial assets and stocks of durables. A shift in the direction of more financial assets means consolidating the liquidity position of the household. It is a timing device. It occurs (a) when the real return to financial assets increases and (b) when the job market goes recessive. Then finally the expenditure system is no longer linear, although the linear version used by Klevmarken and Dahlman (1971) appears as a special case when the two novel features are turned off.
For the time being our ambitions for the household module are low. We need a link between income generated in the production modules of the economy and the domestic markets for goods and services, however. The expenditure system filters total income generated by production units, after tax, through the expenditure system and back as demand in these markets.
Income available for spending period 1 is income generated the period before. For the time being we identify the period with a quarter. If desired, the model layout is such that a monthly specification can be used. To simplify the symbolic representation all Q prefixes, indicating quarterly specification, have been deleted.
For each spending category (i), a desired, or essential, level of consumption is defined (for each household):
CVA represents the addicted level of consumption and ALFA 1, and ALFA 2 measure the strength with which the household wants to maintain this addicted level. Hence CVE may be labelled the desired level of consumption. ALFA2 larger than 1 means an urge to increase consumption over time and vice versa for ALFA 2 smaller than 1.45
For non-durable goods CVA is represented by consumption volume during one or several past periods. For durables CVA is the consumption level desired by the household, which is in turn assumed to be proportional to accumulated household stocks of durables. For saving CVA is replaced by the gap between a desired level of household wealth and actual wealth (see below).
We will distinguish between the following household spending (market) categories:
Non-industrial goods (homes etc.). Prices and volumes determined exogenously outside model.
Domestic industrial goods markets (non-durables, mainly food). Prices are determined in the model.
Non-durable industrial goods, prices determined partly in model and partly exogenously in international markets.
Service consumption. Prices determined in model.
Durable industrial goods. Prices determined partly in international markets. No distinction will be made between durable household goods and investment goods markets. Durables are traded in the same market.
Saving for future consumption. Household’s financial investments.
Currently the credit market is represented by a bank that offers the exogenous international interest rate . Markets 3 and 5 will be supplied by imports as well as domestic producers. Domestic producers for these markets will also sell part of their output abroad. In the model presented here manufacturing firms will sell their entire output in only one of the three markets (2, 3 or 5) for industrial goods.
The following symbols will be used:
C(i) = consumption value, market (i)
P(i) = corresponding domestic price index in market i
CPI = consumer price index
SP(DUR)= spending on durable goods. Includes both household consumption of such goods and investment goods manufactured by firms.
SP(NDUR) = spending on non-durable goods = household consumption of non-durable goods.
SP(SAV) = SAVH =household saving (deposited in the bank).
We start by computing “desired” consumption levels, beginning with nondurable consumption. Then we introduce a desired wealth function and a function explaining durable consumption.
Desired durable consumption is then transformed into desired spending on durable goods. A function explaining desired saving is introduced. All spending categories are then entered into a price, disposable income trade-off formula that runs off a market specified spending plan for each vector of offering prices presented from the suppliers (firms).
After a predetermined number of interactions with the suppliers the then prevailing vector of offering prices is fixed. Households determine the volumes they want to purchase at these prices and markets are “cleared” by adjustment of inventories. No trade takes place until these interactions between producers (firms) and households have taken place. Using actual addicted levels of consumption as weights a consumer price index (CPI) is calculated.
7.2. Nondurable consumption (NDUR)
For nondurable consumption, spending and consumption are identical each decision period (= quarter). No stock building occurs, even though this assumption is violated occasionally in reality (e.g., for clothing and food stored in a freezer). We define the addicted level of consumption by introducing feedback “smoothing” algorithms of the type:
CVA(i) is updated each period. We need a startup value on CVA that is based on past consumption (volume) levels in a way that is consistent with (47). This is obtained by weighing together the historic C/P series with a series of exponentially declining weights.
7.3. Saving (Future consumption)
Saving by households (SAVH) is governed by a tendency to maintain a “desired" ratio (WHRA) between household financial wealth(WH) and disposable income (DI):46
RI = nominal rate of interest
RU = rate of unemployment
WHRA = desired wealth disposable income ratio
WH* = WHRA∙DI = desired wealth in terms of (48)
ULF varies from household to household. It is entered exogenously. The WH/DI ratio is also assumed to depend linearly on the real rate of return to saving (RI-DCPI) and a measure of job-market security (the rate of unemployment RU).
Desired saving in terms of () is now defined as:
which can be reformulated as:
For later updating purposes we introduce the following definition of saving:
Note that desired saving is not the same as actual saving (SAVH).47 The change in household financial wealth is defined as the sum of interest income on actual wealth and new (actual) saving.
Hence:
Updating by this formula takes place end of each period. SAVH is entered at the end of each period when household expenditures have been finally determined.
A household may want to swap part of desired saving for a purchase of durables or wait, and then borrow temporarily or save more than planned. This swap is determined by (A) the return to saving when waiting to buy a piece of durable goods and (B) by an element of cyclical caution. SWAP is derived from (), and
SWAP affects the decision to spend on durable goods directly. A technical note is in place here. In principle we expect SWAP to average out to zero over time, and not affect desired holding of wealth. Under our current assumption that each household is the average or representative household ULF can be obtained directly from aggregate NA data. If so the desired wealth disposable income ratio (48) can be approximated by:
This approximation will however be at variance with (48) in that it will affect desired saving if real interest rates and unemployment rates keep changing for very long periods and do not average out. I will come back to that in the next section on product market arbitrage.
What is finally saved is deposited in the bank. In future consumption spending may be broadened to include also household investments in assets such as homes and financial assets. This, however, requires that both a more sophisticated financial market, and a construction (home building) industry be introduced in the model.
7.4. Durables
The accumulated value of durables is:
where
DP(DUR) = Rate of change in durable goods prices.
SPE(DUR)= Household spending on durables (purchases)
STODUR may remain positive from period to period and deliver a service value to the household that in turn constitutes consumption of that good, or
From (57) follows that if RHODUR is constant, the value of durable consumption can only be varied through variations in the stock of durable equipment. This stock in turn changes because of changes in the price of durables, the service (consumption) outtake of the stock, and purchases of new durables. Purchasing is the action parameter of the household.
Desired purchases of durables are assumed to be geared to a long run desired level of consumption (CVE(DUR}) determined from past consumption levels as in (46) and (47) and a short-term swap factor between saving and spending on durables.
SWAP is brought in from (53). See below for proof.
Finally, the desired level of consumption of durables CVEDUR is obtained by feeding (47) or (48) with past C(DUR)/P(DUR) data.
The novel property of this durable spending function is that in times of job market insecurity or rapid inflation the household may switch between accumulating financial wealth through saving and wealth in the form of durable equipment. SWAP is the switch factor. Since consumption of durables is proportional to the stock of durables, accumulation means more consumption and vice versa. If you don't buy a new car you cannot compensate for this loss of quality of consumption (maintain your previous consumption) by running (down) your car faster. Obviously, the SWAP function can naturally be extended to include the buying of a home, and maybe even investments in financial securities, but we leave that for future upgrades of the model.
7.4.1. Proof of (58)
From equations (55) and (56) we get the actual consumption value of durables as:
Replacing C(DUR) with CVE(DUR) times P(DUR),or desired consumption, gives desired spending (SPE instead of SP) as:
Under certain circumstances, defined by equation (53), households plan to reduce desired durable purchasing via SWAP to increase saving. Hence the last term in (equation (58).
Note here that if SWAP> 0 it follows that CVE∙P>C. Households then allow their consumption of durables to fall below the desired level in terms of (Equation 46). This possibility is intended and motivates that we keep the distinction between CVE and CVA. CVA then is the minimum or addicted level. Extreme circumstances are required for C/P to go below CVA.
7.5. Adjustment to income constraint
With these definitions total (actual) spending adds up to disposable income. By calling in SPE(DUR) (Equation 58) and SPE(SAVH) in (Equation 50) we obtain:48
where SP is actual spending. When confronted with market supplies households will be presented with several “feeler vectors” of offering prices. For each of these vectors the household balances off various spending categories against each another and decides on a preliminary spending plan. To obtain this balancing we introduce the STONE-type expenditure, distribution system mentioned earlier:49
The first additive component in equation (60) tells how total available income is distributed on various spending (consumption, saving) categories in the first allocation round. The second component in (Equation 60) tells how residual income (what is left) is allocated. Note that this residual income may be negative. The conventional approach by Stone (1954) and his followers have been to use only BETA2 (a linear formulation). BETA2 divided by the share of total income allocated can then be interpreted as the income elasticity. As long as we stick to this formulation (i.e. SUM(BETA3)=0) we can draw directly on the empirical results of Klevmarken and Dahlman (1971) with the qualification that they have excluded household saving in their linear income allocation model and assumed total disposable income to be income after tax less saving. By introducing BETA3 we have added a non-linear factor. The idea is that BETA3 is negative for spending categories that increase their share in the long run. As real income (DI/CPI) grows the second factor within brackets grows and the whole elasticity component within brackets [] increases. The problem with this variable elasticity approach is how to split Klevmarken and Dahlman (1971) somewhat biased estimates on the time average of {BETA2(I)+ BETA3(I)∙CPI/DI} into BETA 2 and BETA3 coefficients. For the time being we assume that BETA3=0, which allows a more direct access to Klevmarken and Dahlman's results.
After N confrontations with suppliers in each market the Nth offering price vector is fixed as actual prices. Consumers calculate what they will buy of goods and services at those prices from Equation 60 . Volumes not bought add to suppliers’ inventories. Desired saving in Equation 50 has influenced each market trial. SWAP has been shifting depending on DCPI. However, no trade has taken place until now. After the Nth confrontation SAVH is finally determined residually as:
7.6. Computing the consumer price index (CPI)
The consumer price index is determined ex post in the Nth market trial on the basis of the P(I) vector by a conventional weighing formula. It is of interest to experiment with different weights. I suggest at least two systems of weights. The conventional:
and the less conventional with “addicted” consumption levels as weights:
from equation (47) or (48).
In (Equation 62) C and P refer to one period back in time.
8. Product market price determination, import competition and inventory adjustment
Production plans have been set by firms in Section 4.3, and firms’ planned supplies in product markets preliminarily, after having tested households’ willingness to buy at offered prices, in Section 6. Household purchase plans have been determined in Section 7. There have been trial interactions between suppliers and households, but no trades so far. We have now reached the stage when ex ante supplies and demands meet, market transactions are conducted, and price and quantities determined. This is again accomplished through search in product markets.
Products are in principle not homogeneous, but the trial market interactions in Sections 6 and 7 are assumed to have perfectly evaluated the quality differences between products in each of the four markets such that technically there are no quality components in the product price for that market. Product value, deflated by the endogenously determined product price in that market is therefore a measure of product volume, and prices are identical per unit of output. Firms in the model therefore cannot, in the present set up, explicitly compete by differentiating their products. In fact, firms are competing with their profit margins by controlling wages, the recruiting of workers, investing and organizing production efficiently. Differences in profit margins therefore derive from labor market imperfections (differences in wages) and/or from differences in production efficiency.
Four market functions are recognized. First, we model how imports compete with domestic producers. Second, we specify the relationship between producers and market intermediaries (wholesale and retail sectors). Third, we model the final interactive market search between suppliers and households, and fourth, conclude with the final inventory adjustment that clears the market.
8.1. Imports
Imports enter Sweden much in the same way as exports leave Sweden. Changes in price differentials between Swedish domestic and foreign markets push goods flows in the direction where better trading margins can be fetched, that is where prices are highest. Thus,
for
the market import ratio:
else
If domestic inflation is faster than foreign inflation IMPR gradually edges upwards and vice versa. α determines then rate at which IMPR reacts to that relative price change. Note that a change in the exchange rate will appear as an exogenous change in α.50
As with exports, importers or foreign exporters react with a lag (one quarter). Because of transport distances we assume no trade-off between domestic and foreign markets within the period. Once IMPR has been decided based on past quarter data, delivery volumes are fixed and assumed to be delivered in full at whatever price the market determines. Thus, in each interaction between suppliers and households within one period, the same fixed import supply volume is entered.
8.2. Market intermediaries (not yet in program)
It is unusual for households to buy their goods directly from producers. Wholesalers and retailers enter in between as distributors. Such intermediaries mean a lot for competition in consumer goods markets. Since this model does not operate in terms of differentiated products and direct product competition in each market, wholesale and retail intermediaries won't figure in their most important capacity, namely as intermediate market agents. They only appear in their third function of moving the goods from the factory gates to the retail shops. With this in mind it becomes reasonable to lump them all together into one body for each market that charges a markup for its transport service, much in the same way as the service sector is treated in Section 3.
There is one important distinction. Firms hold inventories and carry the risk of unpredictable consumer behavior. Hence, the following happens between producers and households in each goods market. Intermediaries are assumed to be myopic in their expectations since they can always correct their mistakes in full the next period. Based on last quarter’s volume sales, they assess their inventory position and plan initially to order new goods from producers, to move stocks to optimum levels, and to realize a sales volume increase of the same magnitude as the previous quarter. Hence, intermediaries enter the market each quarter with the following opening bid:51
ORDV stands for order value and XSV for expected sales value of the same product. Producers tell what they will supply at their offering price. Intermediaries respond by offering to buy:
SPEC is a time reaction coefficient (SPEC for speculation) that determines the rate at which dealers fill up their warehouses. This rate depends on how much they expect prices to change over the next four quarters compared to the price they are offered. These market iterations continue for an arbitrary number of rounds. When stocks have been updated intermediaries stand ready to supply households with:
at EXPP and in competition with an import volume supply already fixed. Market prices are then determined as described in the next section.
Profit margins, labor demand and productivity are treated as in the service industry specified by equations (32–36) in Section 5. Profits from this sector feed into households since they consist of either wages to employed labor or owners’ income.
8.3. Final product price determination
Market price expectations govern firms’ supply decisions. Based on installed production capacity, capacity utilization, and product inventories each firm, each quarter readies a production plan based on product, labor and financial market price expectations that satisfies preset profit margin MIP targets. Each firm then adjusts its employment through recruitment and layoffs to support that plan. That may not be possible without changing wages and/or employment compared to original wage expectations, which may require another revision of the production plan to be compatible with MIP targets as described in Section 4.3. This is repeated several times before the quarterly production plan is finally determined. After production has been diverted for exports, as described above, supplies from individual firms in the domestic markets are aggregated and offered to households and firms at expected prices PRELPDOM. Demand for investment goods in durable goods markets is determined by firms' individual investment decisions
Household demand derives from the expenditure system introduced in Section 7. This system tells how households will divide up their disposable income determined in the previous quarter between saving, on the one hand, and various consumption categories, including household demand for durable goods, on the other, and in response to the ex ante aggregate price vector PRELPDOM offered by firms, at which firms are willing to supply:52
With foreign supply (=SUFOR) added, total initial domestic market supply is:
Initial firm supply is entered from the production system after labor market search, and when the production plans have been finally fixed based on known employments.
Households now tell firms what volumes they are willing to buy by feeding the PRELPDOM price vector into their consumption function. Based on this information firms respond by stepping up the offering price slightly if total demand (volume) in each market turns out to be larger than expected and vice versa.
Households again respond to this revised price vector by telling a new demand volume and this is repeated a preset number of times each quarter within the limits set by total supply volumes in Equation 69 and total household income. Thereafter prices and household purchases for the quarter are finally determined.
Household saving can now be calculated residually.
Firms now know how much exports and households together have taken out of their production and what has happened to their product inventories.
Since we have not yet individualized final firm quarterly supplies in the market a substitute distribution algorithm for inventory change has to be entered. Total change in finished goods inventories is thus determined after the Nth product market iteration and is distributed proportionally to size over firms. For individual firms this may mean that stocks will exceed upper storage limits or fall below minimum storage requirements. This is solved by setting STO equal to MAX or MIN STO respectively for these individual firms. The adjusted total change in STO is then distributed proportionally over the remaining firms.
This product market arbitrage is what is currently in the model code. It is a stylized version of the quarterly planning practice observed in large firms in Eliasson (1976a). This stylized version is, however, compatible with an immense number of detailed variations that we abstract from until we have decided when to introduce a micro version of the household sector. It is true, for instance, that large firms regularly begin budgeting and planning by predicting total market change, and then, given their competitive situation and price strategy, predict how large a share they will capture. This procedure is represented by the sales forecast in Section 2.3.1 from which production planning begins. A possible alternative production supply sequence of theoretical interest would be to begin with a strategic price expectation of what firm management think the market will absorb and then first compute a production plan with normal capacity utilization and supply the market with as much as is compatible with optimal inventories at the end of the quarter. The firm then checks for MIP profit target satisfaction, and when the necessary internal adjustments (including changing wages, recruiting, or laying off workers etc.) for profit target satisfaction have been concluded, it fixes the quarterly production plan and enters the market test as already in the model code. If we think this is empirically interesting, we could also make each firm engage each quarter in an internal short term profit maximizing exercise where strategic price expectations are matched with different production plans given existing short-term capacities to produce. It would also be technically straightforward, but demanding on computer capacity, to have firms overhaul their entire production plan after each new price vector has been fed back from t0he household interaction. The evidence from Eliasson (1976a), however, is that production plans tend to remain fixed during quarters.
8.4. Model pseudo code
Written jointly by Gunnar Eliasson, Mats Heiman and Gösta Olavi
The MOSES computer simulation program is written in the APL language. In this publication we do not include a listing of the program; instead, we give the following “pseudo-code” specifications, which in a more English-like syntax presents the APL program.
The computer simulation runs sequentially through time in a straight-forward way. Unless otherwise indicated by separate instructions, the equations are executed one by one. (For one year, the quarterly blocks 3-9 are repeated 4 times).
Note that, this being a micro-based model, the execution of one equation often means several assignments, for firms, markets, household groups, etc. We do not use an indexing system in the pseudo-code; in general, it will be clear from the context if equations (and variables and parameters) refer to global entities or to firms, markets, etc. This information can also be found in the variable listing which concludes this section.
The pseudo code was originally appended to this publication as an Appendix. It is not republished here, but is available on line. See further underEliasson et al. (1976).
Footnotes
1.
There are some additional less important exogenous variables that I leave for later technical chapters. Entry of new firms is exogenous, but the exit of firms is endogenous.
2.
Questions are asked about the distances A to B and C to D in Figure 2. See further (Virin, 1976).
3.
Note that the initial state also includes the rest of the economy, including complete and consistent industry stock and flow accounts. While the Planning survey provides a new initial state every year, to obtain NA level macro accounts requires a major statistical effort that can only be done now and then. Fortunately, the model simulates complete and consistent micro to macro accounts for the entire model economy by quarter. We can therefore reset the initial state at any time by running the model to the desired quarter using known (for historical simulations) exogenous variables and reload it by actual firm data from the Planning Survey. This method should be useful, and is probably the only practical method for empirical cost benefit type economy wide studies, to position the entire economy on a “correct” initial state.
4.
This observation is an instance of what Leibenstein (1966) calls X-inefficiency or a version of slack. Note here Carlsson's measurements of such slack in Swedish manufacturing, and especially as regards the degree of capital utilization or (A-B) + (C-D) in Figure 2(Carlsson, 1972).
5.
The Pseudocode, appended to the original version of this document, has not been republished here. It is available digitally from the journal. For that see Eliasson et al. (1976) in the reference list.
6.
In a static equilibrium world with (assumed) fixed production structures MIP targeting would approximate maximum ex ante wealth creation. I will come back to this “problem” below.
7.
Also see Eliasson (1976a).
8.
This requires that INV = DK1 + RHO K1 – K1DP + DK2, where INV is gross investment.
9.
Note that K2 is broken down into several components in the next Section.
10.
There is a problem here. If realized inflationary gains are listed under C the costing principle used to obtain M has to be based on a replacement valuation of raw materials and intermediate goods. This is a problem we have to face when the model is fed with real firm data.
11.
The regular contacts with firms of my department at the Federation of Swedish Industries made clear that this was a serious problem. One of our staff researchers together with a researcher from Stockholm University has therefore authored a handbook on inflation accounting, Bröms and Rundfelt (1974).The book is already in its second printing.
12.
Stylized such decision processes have been modelled during recent years based on the famous Dantzig – Dantzig and Wolfe (1961) algorithm. The point made here is that we are not modelling decisions but the negotiations preceding the agreement on a plan needed to mete out responsibilities. This distinction is important.
13.
See example in Eliasson (1976a).
14.
This formula is identical to an exponentially declining weight system. Also see Eliasson (1974a) where this adaptive expectations algorithm was first published.
15.
We have tried to estimate some of the individual firm coefficients above by direct interviewing of executive staff in one very large Swedish firm. The results turned out quite successful in terms of improving historic tracking of firm data. Further efforts of this kind are planned. To this can be added the possibility of imposing an exogenous adjustment of expectations in individual firms.
16.
This is however the place to enter an explicit CHQ allocation function should we decide later to expand the firm model to a multidivision firm with an explicit financial asset management operation, and also explicitly enter their foreign subsidiaries as separate operational units. As for empirical data that expansion is already prepared for in that the Planning Survey of the Federation of Swedish Industries already collects data by division for the large firms, and that those divisions (for instance six in Volvo) currently operate as individual firms in model simulations. For the time being we however only collect data on domestic divisions and will wait for a large IUI study on foreign subsidiaries to be ready (See further Section 6.1 on export functions).
17.
Note, however, that NW is not market valued. Expected future profits should not affect the valuation. NW is residually calculated in a balance sheet where assets are valued at replacement costs. See Figure 7.
18.
An account of the tax system of the model is in progress for separate publication. (See republished in this anthology).
19.
This is the interdependence between C and D in Equation 1 mentioned in the previous Section.
20.
Even though in reality it is not. See Eliasson (1976a).
21.
Also remember from Section 2, that instead of imprecise rates of return, firm management for the same reason use profit margins as proxies for rates of return to monitor profit performance in budgeting. Even though business managers as a rule are unfamiliar with neoclassical production theory they sense intuitively that there is something both conceptually and operationally unclear about the rate of return to capital that is a ratio of the profit flow to a stock of capital that in turn is related to the expected future flow of the same profits. Even economists sense a contradiction here (Eliasson, 1976a).
22.
87 percent of the number of firms surveyed. See Virin (1976).
23.
Firms do not “recognize any Q” larger than Q in 3’ as economical. Hence there will be a kink in QFR that makes dQFR/dL = 0 beyond L in 3’.
24.
In 1975 L data on point 3 were not asked for.
25.
After this positional assumption has been entered, however, RES is endogenously updated from quarter to quarter by the model.
26.
It is quite another thing that measures of the economic value of physical capital appear in the balance sheets of firms.
27.
A harmonic average formula is used here to merge new investment vintages with the existing capital stock into a new capital stock.
28.
Note that (27) presumes that no raw materials or semi manufactured goods enter production. This is so in the present version of the model. See however Section 6.2
29.
SOLVE only needs to be activated when SAT is reached along a non-linear segment of the recognized output limits. It gives an approximate numerical solution using the Newton-Raphson method. See further (4.3.12) in pseudo code.
30.
Path CD is a nonlinear segment and the Newton Raphson method has to be used to solve for QPLAN.
31.
Note, however, that the Swedish AMAN laws constitute a legal restriction to the attainment of SAT until after a 6-month delay. See section 5.5 below.
32.
For instance, between US and European firms. See Eliasson (1976a).
33.
Note that we are now in conflict with the profit maximization rule of neoclassical economics. If the initial Q plan happens to be at a point where EXP(P) ·dQRF(L)/dl > EXP(W) we should move north to increase profits. Now we are mowing down, decreasing profits but increasing profit margins.
34.
See section 5.5 below. A first analysis of the macroeconomic consequences of the AMAN laws is found in Eliasson (1976b).
35.
Wholesale and retail sale. See Section 8.2 on market intermediaries in Section 8.
36.
Even though not well supported by econometric evidence (Eliasson, 1972b; Eliasson, 1974b).
37.
All Z indices, identifying the service sector have been deleted for simplicity.
38.
Note that this does not mean that all redundant workers are in AMAN. This is only the case when the firm cannot reach SAT before being on QFR(L), where no redundancies exist.
39.
This will hold also when we introduce intermediate goods and raw materials later in this Section, since there is no reason to expect differences in purchase prices for the same inputs in different Swedish subsidiaries.
40.
Remember from (3) in section 21.1. that M = 1- LW/QP.
41.
This price elasticity of exports should be possible to determine econometrically for individual firms when a sufficiently long panel of firm data has been collected in the Planning Survey.
42.
There will always be a problem to decide which variable each stock type should be related to. Since practically all sequential stocks follow sales indirectly we use sales to avoid confusion with too many scales.
43.
Divided by EXPP.
44.
This is analogous to the household-firm interaction, but it runs in the opposite direction.
45.
In most model experiments so far, we have chosen not to distinguish between CVE and CVA and made ALFA1=0 and ALFA2=1. We expect this feature to be more important when the household module has been micro specified. See however comments to proof of (9) below.
46.
Temporary saving for some purchase goal, like a home, is not allowed by (48). This possibility is introduced through SWAP below.
47.
In fact, SPE(SAV) = (WHRA DI- WH) + DI SWAP. SWAP is defined below in conjunction with the treatment of durable goods purchases.
48.
Occasionally saving may turn negative. This also means that total spending is larger than DI. We can however still keep DI as the income constraint.
49.
To obtain a volume estimate of desired durable spending needed in (60) for balancing against the price vector we deflate SPE(DUR) in (9) by past period P(DUR).
50.
Note the possibility of studying the economy wide consequences of import controls at the level of an entire market by making α = o, or simply fixing IMPR.
51.
All variables quarterlized.
52.
Note that we treat firms as a group here. The offering price hence is the average offering price.
53.
For an extension of the separable additive targeting formula (1) in Section 2.1.1 with taxes included see Eliasson (1976a). Also see Eliasson (1976c).
54.
For instance, by using an average of past, say 5 years.
55.
(7.3) and (7.4) are derived from (5.2). When CHBW is reduced as in (7) only INV and CHS are affected. Since CHK1 = β·CHS/α we obtain (7.3). To obtain (7.4) we use (2). A reduction in CHS leaves DP(DUR) and RHO unchanged. Hence (7.4).
56.
The factor RISCO may be entered as a constant, or be represented by the past variation in, say, MS/NW. It may be updated from period to period.
57.
See my capital budgeting theory of investment in Eliasson (1969).
58.
RW is in the neighborhood of – 0.3 and has been fairly stable over time.It may however vary since it depends on the length of trade credit extensions and therefre on interest rate developments. Under tight credit market conditions, for instance, firms may delay payments. See further on trade credit functions in Eliasson (1969) and Eliasson (1972a).
59.
Note that we deliberately mis specify here, since K2, as used in the model, includes finished goods inventories.
60.
NB. No taxes or income transfers in this simplified presentation.
Appendix A
Proof of additive objective function (1) in section 2.1.1
Assume no taxes.53
Symbols are defined in Section 2.
Introduce the cash flow identity:
Definition of gross investment spending:
∏ = Operating profits (gross), inclusive of depreciation
RI = Average rate of interest on net debt (=BW)
K1 = Replacement value of production equipment on which the depreciation rate (ρ) is applied to obtain depreciation (ρ∙K1).
k1= The corresponding volume measure, obtained by deflating K1 with the investment goods deflator P(DUR)
K2 = all other assets, same valuation
NW = Net worth residually determined from total assets: A ≡ K1 + K2 ≡ BW + NW
A = total assets
Now reshuffle terms in equation (A1) and insert in (A2:
From the definition of the nominal rate of return to net worth:
Ɵ is the rate of dividend payout of NW.
It furthermore follows:
Since
(Ѱ = leverage factor)
we obtain
But
Thus
QED
Appendix B
Technical specification of investment-financing block (sophisticated version, not yet in pseudo code or program)
From equation (7) in EXP section 2.3 (assuming ß = 0) we obtain:
1.1
1.2
1.3
2. (Definition)
3.1 Calculate from 1.3
K1 year by year to horizon (=H)
3.2 Enter long term expected DP(DUR) (=EXPLDP(DUR)from 1.1 above and RHO (exogenous}
3.3 Calculate INV year by year to H from A2 in previous Appendix A .
Note that we choose to obtain the "trial" INV paths this way rather than feeding the preliminary EXPL(DS} etc. into the production block to derive (indirectly) investment requirements. Cf. discussion in Section 3 on calculation of INV from balance sheet rather than through production system.
3.4 Enter QFR(L} with last period L from Section 4.4.
Enter NU = normal expected long-term capacity utilization rate.5455
Calculate NU∙QFR(L)
Assume no change in L and that DTEC=DQTOP
3.5 Enter INV from 3.3
Quarterlize INV. Deflate by EXPLDP(DUR).
Calculate DQTOP1 each year to H
3.6.2 Calculate
NU∙QFR(L) on Horizon year (L same as now)
3.7 On H
M:=(EXPLP∙NU∙QFR(L)-EXPLW∙L}/(EXPLP∙NU∙QFR(L))
(Same formula as Equation 3 in Section 2).
3.8 Compare M with TARGLM.
Check for SAT
The Planning Survey of the Federation of Swedish Industries (Virin, 1976) that is used to initialize the model includes division data for practically all large Swedish firms. Note therefore, that if we decide later to split the firm into several production units held together by a financial CHQ function, this is the place to do it.
3.9.1. If SAT go to (4.2)
3.9.2. If not SAT lower EXPL(DS) with X percentage points and repeat until SAT
4.1 EXPRIL:=EXOGENOUS
EXPRIS:=EXOGENOUS
4.2 Enter EXPLDS from (1.1) (or final value), EXPLDP(DUR) from (3.2) and M from (3.7) in (4.3) to obtain MAX Ѱ:
4.3 Calculate
(See derivation in Appendix
(5. Enter business cycle in S and calculate consequences for M and INV in H year plan. Note that the rate of capacity utilization has to be entered as determinant of quarter-to-quarter INV)
5.1 Calculate CHDLIQ:=LIQD-LIQ from (13) below
5.2 Calculate for next year:
and note definition of γ from Equation 16 in section 3.4.
5.3 and then for following years make CHDLIQ:=CHLIQ
5.4 DIV: = Ɵ∙NW(LAG)
Ɵ:= EXOGENOUS.
Note that LAG refers to the previous year. DIV adds to total income in the household sector.
6.1 Calculate
Note that formula (6.1) is identical to (5.2) except that NW has been lagged one period reflecting the fact that dividends are normally calculated on profits realized some period before. When NW is measured for the current period (5.2) is a book identity and in (6) we have simply solved for NW.
6.2 Calculate
BW:=BW + CHBW
6.3 Calculate
Ѱ= BW/NW
7.1 CHECK for Ѱ≤MAXѰ (see Appendix C) each year
IF SAT go to (10)
IF NON SAT lower net borrowing to satisfy Ѱ≤ MAX Ѱ restriction each year
7.2 Add up reduction in CHBW each year 0 to H
and divide by H to obtain annual average: =X
7.3 Reduce EXPL(DS) as follows:
Reduction (in percentage points) of planned long term annual growth rate in:55
S :=Y=(X∙(I-RI))/S(LAG)
7.4 Reduce INV/K1 by
Reduction in planned INV per year:= Y∙ S(LAG)∙ β/α
7.5 CHBW:= CHBW -X for each year.
Note that CHBW so calculated for first year defines maximum borrowing allowed for next year (Long term and short term).
8. We now have the long-term (H-year) plan + annual budget (by quarter):
INV from (7.4) and (2)
K1 ditto
DS from (7.3)
DA from (1.2) and so on.
Quarterlize INV as in (3.5) and whatever else that is needed by quarter.
9. Tentative. Enter business cycle in long term S by applying the factor CYCLE in Section 2.
Calculate consequences for M and INV and LIQ (see below) in H-year plan. We then enter the rate of capacity utilization to determine quarter to quarter INV.
B.1. One year long- term borrowing decision
10. Add CHBW in (9) for all years 0 to H.
CHBW:= Y = Total new borrowing long term
Note that Y is expressed in expected current prices each year.
11.1. Calculate long-term borrowing for year immediately ahead as:
CHBWL:=(Y/H)(1+ γ(RIS -RIL)/RIL)
Note the possibility of individualizing RIL and making it dependent on the firm’s debt equity (gearing) ratio Ѱ. RIS is the short-term interest rate and RIL the long term rate.
11.2. If CHBWL in 11.1 for first year is smaller than CHBW in (9), make up for difference by borrowing short term (CHBLS).
12. Add one quarter of CHBW (total) to cash position beginning of each quarter and calculate EXPQLIQ from long term plan.
13. Calculate desired LIQ as: LIQD = F(S ,expected excess cash outflow).
Excess cash outflow is defined as in the following Appendix C, but for next year only.
14. Calculate expected LIQE from (12). The expected cash outflow
defines the firm’s short-term (next year) liquidity status as seen from within the firm.
15. Short-term target modifier
Allows short term operations M-targets to be temporarily modified downwards because of unexpected or excessively strong negative profit influences. Such modifications relate to specific decisions:
production for inventories
hoarding of people
contracyclical timing of investment
Note that firm management may want to
behave “rationally” in the long run, but dares not because of a risky LIQ position.
be rational and take drastic action, but social and other considerations prevent it.
Contrary to the AMAN laws in Section 5.5 (also see labor experiments in Eliasson, 1976b), which apply to each firm all the time, these are ad hoc modifications that we may enact exogenously. I consider this possibility empirically important.
16. Calculate from Equations 14; 15 maximum contribution from LIQ next quarter as:
CHLIQP: = LIQE - LIQD
Note that CHLIQP may be negative.
B.2. Investment decision
17.1 Investment finance allocated next quarter (final decision):
INVF:=M∙QPLANS - ∙QPLANCHS-(1+RAM)∙BW-DIV-CHLIQD
Quarterlize INVF to QINVF.
17.2 QPLANS is obtained from PROD planning block in Section 4 as:
QPLANS: = QEXPP ∙ (QPLANQ - OPTSTO + STO)
17.3 Calculate (from Section 6) planned intermediary inventories build over and above planned quarterly use. Call this CHTESS.
17.4 Enter QINV from (8).
QINV:=MIN (QINV, QINVF-QCHTESS)
Final decision. Repeat every quarter.
18. QINV from (17.4) enters as final money demand in capital goods markets. (Next period).
Market DP(DUR) determines volume QINV that updates production system.
19. Residual LIQ is invested currently (each quarter) at (RIS - XI).
XI:= Exogenous difference between short-term borrowing and deposit rate, and equal to profit margin in banking system).
Appendix C
Derivation of the maximum gearing ratio
The global objective function of the model firm has been defined by Equation 1 in section 2.1.1 as:
Ѱ= BW/NW = gearing ratio or leverage
Ɵ = DIV/NW= dividend payout rate
DEFL = chosen general price deflator e.g., CPI
BW + NW = A
α = S/Aβ = K1/A K1+K2 = A
α = S/A
β = K1/A K1+K2 = A
Thus (1- β) =K2/A and
K2 = ∙S
From Section 2.1. the nominal (money) return to A becomes:
Define the risk rate associated with borrowing (as assessed by the firm) as:
RISK=RISCO∙ (EXPECTED EXCESSCASHOUTFLOW)/ NW
RISK=RISCO∙ ((RI+RAM) ∙BW)+(K2∙CHS)/S-M∙S)/NW
RISK is defined to be comparable to RRN or RI.
RAM = rate of amortization of BW.
We know that
Thus:
Assume MAXѰ to be a linear function of the risk corrected return over the borrowing rate:
Then from equations (4) and (A6):
QED.
Appendix D
Provisional investment financing module
This provisional INV-FIN module is designed to be used in a “slimmed” version of the model.
D1. A capital budeting investment function
The investment function that updates the production system is of the capital budgeting cashflow type:57
Investment is assumed to be equal to current gross (profit) cash inflow (M∙ S), plus net inflow of borrowed funds (CHBW), less mandatory financing of current assets (RW∙CHS) and interest payments (RI∙BW). The assumed mandatory claim on financial resources from short-term trade assets is assumed to be proportional (RW) to the change in sales value (CHS) which is common approximation in a budgeting or planning practice.58
In this simplified version the firms' rate of borrowing, and thus in the end their current investment spending become determined by equation (A16) below by the relative return to capital and to depositing cash in the bank at the current interest rate. INV is determined at the end of each quarter by the data set of the same quarter. It affects the production system in the next quarter.
D2. Determination of the rate of borrowing
The borrowing decision depends on the difference between the nominal expected return on total assets (RRN) and the rate of interest (RI). By definition:
Kl = The "value" of production equipment
NW = net worth of firm, residually estimated from the balance sheet, where all assets are valued at current reproduction costs.
Define the stock of current assets as:59, 60
and total assets (see table) as:
A = K1 + K2 = BW + NW (A12) From (A4) in Appendix C follows that the rate of return on total assets is:
(A12)
RHO = rate of depreciation on production equipment. Same rate as in production system.
DP(DUR) =rate of change in capital goods price index which is endogenously determined elsewhere in model.
By definition:
Assume that the rate of net borrowing is linearly dependent on the difference between the nominal return to total assets and the nominal interest rate (long term).
Thus:
ALFA > 0
BETA > 0
RI(LONG) =Long-term interest rate. And so:
Equation (A16) applies each quarter. Updating of K1 is by Equation A14 and working capital stock and BW by Equations A11; A15e. We can then generate a rough balance sheet of each firm each quarter and calculate NW residually as in the table below:
| Balance sheet of individual firm consistently generated each quarter | |
|---|---|
| Assets | Debt |
| K1 | NW (Residually determined) |
| K2 | BW |
| SUM = A | = A |
Appendix E
Household demand module
E.1. In data:
– I =market = consumption category
– CVA initial (see Equation 47 in Section 7.2).
– P feeler price vector from EXP section 2.3 and used in business plan in section 4.3.
E.2. Aggregation of all incomes gives total household disposable income DI from labor market and business plan in Section 6.61 Under this specification aggregation will be to all households. This means that total disposable income is SUM QW in manufacturing, service and Government sectors.
E.3. Consumer price index (CPI):
, or
Note that this definition includes the service sector from section 5.
E.4. General transformations
Addicted consumption level:
Desired level:
E.5. Non-durable consumption (2, 3, 4)
Note that SP= spending.
Desired spending :
From Equations 17–19, we obtain:
E.6. Durables
Desired spending:
From Equation A18 and A19:
E.1.7. Saving
To obtain the "addicted" financial Wealth/Disposable income ratio WHRA use Equation 48 in section 7.3 on past WH/DI for T years.
Desired saving:
Note that in Equation A20:
Updating
E.8. Adjustment to income constraint (by quarter)
which is the same as Equation 60 in section 7.5.
Note that SPE(I)is obtained from Equations A24; A28 above after division by Equation 4, and that SP(I) can be split into a price and volume component. Suppliers' offering price is entered at two places to calculate SP(DUR). SP(DUR) and then divided by the same price to obtain spending volume as a return signal to suppliers.
E.9. Market interaction with suppliers (final price determination)
See Section 8 were final prices and consumption volumes are determined.
References
-
1
The transactions model of the U.S. economy: The treatment of the business sectorMimeographed Paper Presented at the NBER Workshop on Microanalytic Models at the Urban Institute, Washington DC. (May 1975).
-
2
Macroeconomics through Microsimulation: Simulating Humphrey-HawkinsPaper Presented to the 1976 AEA Conference in Atlantic City, September 16-18.
-
3
Labor turnover, segmentation and rates of unemployment. A simulation-theoretic approachProject on the Economics of Discrimination, University of Maryland, (August).
-
4
A microsimulation of the macro economy with explicitly represented money flowsAnnals of Social and Economic Measurement.
-
5
Inflationsredovisning–Ett förslag till prisjusterad årsredovisningFederation of Swedish Industries, Ekonomiska Utredningsrapporter, Serie A Nr 13 (December).
-
6
Monetary and Fiscal Policy Experiments on Four Macro Economic Modelsforthcoming, Industrikonjunkturen, Spring 1977.
-
7
The measurement of efficiency in production: an application to Swedish manufacturing Industries 1968The Swedish Journal of Economics 74:468.https://doi.org/10.2307/3439287
-
8
A Behavioral Theory of the FirmA Behavioral Theory of the Firm, Englewood Cliffs, N.J.:Prentice Hall.
-
9
The decomposition algorithm for linear programsEconometrica 29:767.https://doi.org/10.2307/1911818
-
10
Myopic Optimizing and Rules of Thumb in a Micro-Model of Industrial GrowthThe American Economic Review (March.
- 11
-
12
Kreditmarknaden Och Industrins Investeringar - En Ekonometrisk Studie Av Företagens Kortsiktiga InvesteringsbeteendeUppsala: Almquist & Wicksell and Stockholm: Industriens Utredningsinstitut (IUI).
- 13
- 14
-
15
Capital transfers, taxes and International corporate operationsEconomic Research Reports Nr B2, OECD Paris and Stockholm, Federation of Swedish Industries (April).
-
16
International Competitiveness An Empirical Analysis of Swedish Manufacturing, Research Reports B3Stockholm: Federation of Swedish Industries.
-
17
Economic Research Reports, Federation of Swedish IndustriesStockholm, Economic Research Reports, Federation of Swedish Industries.
- 18
- 19
-
20
Competition and Market Processes in a Simulation Model of the Swedish EconomyAmerican Economic Review 67:277–281.
-
21
Two Papers on Planning and Efficiency, Economic Research Reports, Series B (October)Stockholm: Federation of Swedish Industries.
-
22
TECHNICAL SPECIFICATIONs – Model Pseudo Code, PART III, in Eliasson, Gunnar, A Micro – Macro Interactive Simulation Model of the Swedish EconomyEconomic Research Reports, Series B (December 1976), Federation of Swedish Industries, Stockholm. This technical pseudo code is available on line from the International Journal of Microsimulation.
-
23
Essays in Positive EconomicsThe methodology of positive economics, Essays in Positive Economics, Chicago, Ill, The University of Chicago Press.
-
24
A Theory of the Consumption FunctionPrinceton: Princeton University Press.https://doi.org/10.1515/9780691188485
-
25
Economic Essays in Honour of Gustav CasselPropagation problems and impulse problems in dynamic economics, Economic Essays in Honour of Gustav Cassel, London, Allen and Unwin.
-
26
World Inflation and the Small Open Economy, Economic Research Report no.17 The Federation of Swedish Industries (November)
- 27
-
28
A Multisectoral Study of Economic Growth (Second Edition 1974)North Holland: Amsterdam etc.
-
29
Den Privata Konsumtionen 1931–1975 (IUI)Den Privata Konsumtionen 1931–1975 (IUI), Uppsala.
-
30
Three Essays on the State of Economic ScienceNew York: McGraw Hill Book Company Inc.
- 31
-
32
A Study in Monetary Analysis (Acta Universitas Stockholmiensis)Stockholm, Göteborg, Uppsala: Almqvist & Wiksell.
-
33
Economic Cycles: An Analysis of Underlying CausesCambridge, MA: Wright-Allen Press, Inc.
- 34
- 35
-
36
Microanalysis of Socioeconomic Systems: A Simulation StudyMicroanalysis of Socioeconomic Systems: A Simulation Study, New York.
-
37
Policy Exploration through Microanalytic SimulationWashington DC: The Urban Institute.
-
38
An efficient method for finding the minimum of a function of several variables without calculating derivativesThe Computer Journal 7:155–162.https://doi.org/10.1093/comjnl/7.2.155
-
39
A method for minimizing a sum of squares of non-linear functions without calculating derivativesThe Computer Journal 7:303–307.https://doi.org/10.1093/comjnl/7.4.303
- 40
-
41
Theories of decision making in economics and behavioral scienceAmerican Economic Review 49:253283.
-
42
Linear expenditure systems and demand analysis: an application to the pattern of British demandThe Economic Journal 64:511.https://doi.org/10.2307/2227743
- 43
-
44
Industrins Utveckling 1974-76 Enligt Industriförbundets Planenkät 1975/76Specialstudie D, Industrikonjunkturen (Spring).
-
45
The quantification of judgment: some methodological suggestionsJournal of the American Statistical Association 62:1105–1120.https://doi.org/10.1080/01621459.1967.10500920
-
46
Adaptive Economic ModelsOptimization and evolution in the theory of the firm, Adaptive Economic Models, Elsevier.
-
47
Econometrics as pioneering in nonexperimental model buildingEconometrica 37:369.https://doi.org/10.2307/1912787
Article and author information
Author details
Acknowledgements
The above is an unabridged version of pages 11 through 195 in Economic Research Report B15, December 1976, Stockholm: Federation of Swedish Industries. Identical versions were published in December 1976 by IBM and the Industrial Institute for Economic and Social Research (IUI). a few repetitive paragraphs have been deleted, a few subheadings inserted for clarity, and some cross references and a few clarifying sentences added. Language errors have also been corrected. Furthermore the numbering of equations has been changed, and a few editorial modifications made for the text to conform to the Journal style. Otherwise it is identical to the original.
In the Foreword (not reprinted) the President of the Federation, Axel Iveroth, acknowledges that this micro to macro modelling project was started at the Federation in late 1974 as a joint project between the Federation, IBM Sweden and the University of Uppsala, and that the project will be transferred, as of January 1, 1977, to IUI when Gunnar Eliasson becomes its president. See for instance Brook and Teigen (1977).
Publication history
- Version of Record published: December 2, 2024 (version 1)
Copyright
© 2024, gunnar.elias@telia.com
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.