
Modelling Financial Derivatives Markets in a Firm Based Evolutionary Macro Model (MOSES)-On the market integration of computing, communications, and financial services
- Article
- Figures and data
-
Jump to
- Abstract
- 1. Introduction
- 2. Economic dynamics – the experimentally organized economy
- 3. The MOSES model economy
- 4. Theoretical product development for emerging financial markets- modern financial economics as an intellectual new product innovation
- 5. Games and outside participants
- 6. Making markets more complete- how modern C&C technology influences financial markets and the economy at large
- 7. MOSES simulation results on options and derivatives
- 8. Implications for policy
- Footnotes
- Appendix A
- References
- Article and author information
Abstract
The evolutionary firm based model MOSES of an Experimentally Organized Economy (EOE) is introduced and then outfitted with increasingly more sophisticated financial markets that take us from a stylized industrial banking system (standard in the model), to a (capital) market oriented monetary system, and then on to a securitized financing system where options and market derivatives play a role in allocating financial resources. We study the consequences for long term economic growth of introducing different financial market regimes.
The markets of the financial system and those of the real economy are integrated within the business plans of model firms. The immense micro to macro complexity thereby created reduces the transparency of the economic environment of all actors in the model, including Government as a policy maker, to a fraction of what is needed for informed decisions. The policy maker thereby loses its presumed information advantage of economy wide overview and becomes one bounded rational actor among all other ignorant actors. Because of the strong leverage on the entire economy of its actions the competence and information demands on Government, when conducting policy, however, becomes far more exacting than what is required of any other actor.
When Government engages in ambitious policy making its interventions in markets affect the behavior of all other actors. The entire market regime is therefore affected to the extent that the Central Government often cannot possibly be in control of what it is doing, especially when it comes to the long run consequences of its actions, and therefore often would do better by taking it easy (Eliasson and Taymaz, 1992). We find that financial markets matter for long term economic development and that seemingly insignificant respecifications of the financial market regime can cause considerable differences in long term GNP growth outcomes, amounting to as much as a difference of 1.5 percentage points per annum and a per capita GNP, that is up to 2.5 times larger on the 60 year horizon than in the worst scenario.
The capital market regime is found to outperform the industrial banking system. When introducing a crudely modeled securitized system (call options), the only one our computer system could handle, financial market transactions were, however, speeded up to the extent that resource allocations worsened. Mixing the capital market regime with the simple securitized system generally lowered long run economic growth. Adding options not only increased the speed of arbitrage, destabilizing fundamentals, but also made expectations unreliable and raised the exit rate, notably by making manufacturing firms lose money on their financial investment portfolios. The results on options cannot however be generalized beyond the very specific experimental designs implemented, but they indicate that speeded up market arbitrage, which is what financial derivatives are all about, has mixed economy wide consequences, that may be long term negative in an economy that is not otherwise diversified and robust. While the simulation analysis of the markets for derivates in the MOSES model is still too primitive to allow any empirical generalizations, the results so far should be taken seriously as indicative of possible surprise dynamics that makes it even more important to conduct more inquiries of this kind.
A final methodological note. The excessive demands on computer capacity of the options experiments have prevented us from testing the results for robustness (as for instance in Eliasson and Taymaz, 2000) by running a whole spectrum of experiments with small changes each time in the four different blocs where stochastic specifications are used. The non-linear specifications of the model often generate large differences in very long run outcomes when the stochastic seeds are changed marginally. Hence, the results to be reported should be regarded as explorative, suggesting new credible hypotheses, rather than empirically calibrated results, and also telling what kind of future analyses the new expanded model is capable of.
1. Introduction
The financial system influences the real economy and economic growth through intermediating the market allocation of resources. The interest setting process is central to that allocation. The financial system, however, is also an intermediary in the reallocation of wealth and real resources over markets. Changes in financing conditions thus affect the allocation of investments and production structures across the firm population and all relative prices. The consequent increase in dynamic complexity reduces transparency of the economic environment of all actors in the model, including Government as a policy maker. To be noted is that the separability between the financial and real systems often assumed in financial modelling does not hold under these new circumstances of micro- to – macro modelling. Uninformed production firms that dabble in financial markets may thus cause a distortion in asset price structures that lead to miss allocations of real resources and less macro economic growth. Policy makers that erroneously believe that they are well informed are at particularly large economy wide risk.
Another interesting situation arises when distorted asset prices make firms acquire shares, or entire firms at bargain prices focusing on short term capital gains only, and neglecting their manufacturing operations. In that sense this paper addresses the fundamental problem of the efficiency of the markets for strategic acquisitions (Eliasson and Eliasson, 2000; Eliasson, 2000a). The efficient functioning of financial markets and their supporting institutions, hence, is a particular concern. Since the policy maker is such an institution rather than a commercial market agent, an interesting market conundrum may be expected.
The last couple of decades has seen a radical change in the technology of global and local financial market intermediation brought about by the emergence of the fifth generation of computing, or the integration of computing and communications (C&C) technologies. The Internet is currently the carrier of that development (Eliasson, 1995a, Eliasson, 1996a; Eliasson, 1999a; Eliasson, 1999b) defining the potential for radical reorganization of both real and financial global production organization. What is new in the analysis to follow is the explicit and dynamic integration of financial and real market transactions in the business plans of firms. Allen and Gale (1994) estimated that new financial instruments intermediating a more informed and efficient allocation of (financial) risks have lowered the cost of financing and increased the stock market value of US manufacturing firms significantly, given the real (physical) allocation of resources. The last ceteris paribus clause is critical for interpreting their results. We explicitly account for the influence on rational financial and real market agents in determining (a) the allocation of real resources, and (b) economic growth. Hence the allocation of real resources is not given but will be endogenously affected by the introduction of new financial instruments in the simulation experiments to follow. We expect the economy wide systemic effects of that "simultaneity" to be considerably larger than calculated in the static analysis of Allen & Gale. We will also demonstrate how different assessments of risk (or rather uncertainty) based on historical data affect portfolio performance in what we will call an Experimentally Organized Economy (EOE). For this we use the dynamic micro (firm) based macro model of the Swedish Economy MOSES that approximates an EOE.
The MOSES model has two credit market regimes; one (1) exogenous interest rate, and (2) one banking system regime where local supplies and demands for funds determine how the local interest rate of the bank deviates from an exogenous international interest rate, given endogenous cross border financial flows. Under the commercial banking regime (2) firms can borrow at the same domestic interest rate offered by the bank. The model can alternatively (3) feature individual firm interest rates that depend on the firm’s credit risk defined by its endogenously determined debt/equity ratio. In this paper we study what increasingly more sophisticated horizontal financial intermediation does to the economy. One may say that we will upgrade the financial system of the MOSES economy from an (Rybsczynski, 1993):
industrial or universal bank-oriented system, as originally modelled in Eliasson (1976b), in which firms' investment financing was mainly based on retained earnings, to a;
capital market-oriented financial system
...where capital markets, notably the stock market, and the interest rate play central roles, and then on to a
securitized system.
of the US type with sophisticated markets for risks, where options and derivatives play significant roles. We discuss a fourth step in the level of sophistication including also a;
venture capital based financial system
...where industrially competent venture capitalists provide early financial support for entrepreneurs (Eliasson, 1997; Eliasson and Eliasson, 1996; Eliasson and Eliasson, 2000; Eliasson and Eliasson, 2000). For the venture capital analysis a sophisticated endogenous R&D (innovation) based productivity change module has been developed in a separate context (Ballot and Taymaz, 1998).1 We plan tentatively to introduce a venture capital application in that module that endogenizes the selection of winning projects from R&D investments as venture capitalists learn through their investment experience to upgrade the industrial competence needed to make informed selections. Preliminary studies on the role of insiders as information providers to the market (Eliasson, 1990a; Antonov and Trofimov, 1992) conclude the essay.
In this paper we therefore introduce increasingly more sophisticated markets into the model in steps:2
A stock market in which private persons (Households) and specialized investment firms manage financial portfolios. We are particularly interested in the consequences at the macro level of a more “efficient” distribution of risks on industrially competent hands than the commercial banking system can offer.
A market where firms can invest in stocks as an alternative to investments in production capital and manage a financial portfolio. Will this possibility improve or worsen long run industrial performance?
A market in which firms’ individual interest rates depend on market valued financial risks, rather than replacement valued debt/ equity ratios.
A market for trading in financial derivatives (we only model call options). What does it mean for macro economic performance if risks can be more efficiently allocated to the most industrially competent takers?
R&D investments, entrepreneurial investment decisions and venture capitalists.
Insiders as more informed actors in financial markets (see Trofimov, 1995).
Steps 1 through 4 have been fully implemented, and simulation studies conducted.
Steps 5 through 6 have only been included through simple applications.
In the stock market firms’ risks are evaluated and prices on their net worth determined. The market values of firms’ net worth enters their debt equity ratios and therefore influence their individual borrowing rates.
The financial portfolio management function features investment companies that invest individually in stocks and derivatives.
Markets for derivatives, or options, have been around for ages, but are currently manifested in the form of a huge and fast growing trade in complex algorithms that represent estimated values of securities. The latter development is very recent and entirely dependent on the new integrated computer and communications (C&C) technologies associated with the sudden commercialization of the Internet since the mid 1990s. The commercial potential for profitable financial intermediation created by modern C&C technologies is probably enormous. It remains to be seen what that may mean for economy wide performance.
The simulation analyses to be reported on here are complicated in two ways. First, we are studying immensely intricate interactions between actors in the financial and the real production systems of the economy, and the latter "physical" system is not the transparent and well known (to economists) fixed structures of the general equilibrium, or Walras-Arrow- Debreu (WAD) model. Instead the rugged terrain of physical production structures is constantly changing because of the market selection activities going on, a notable exaple of that being the endogenous entering and exiting of firms. This defines market life in what we call a model of the Experimentally Organized Economy (EOE) in which new technology creation, and business decisions are viewed as economic experiments to be tested in markets, and market selection dominates economy wide behavior. In this model the standard separability assumption of financial economics has been done away with by integrating financial, product and labor markets price expectations in the management systems of individual competing firms. Hence, we have to tell a brief story of the EOE through its model approximation MOSES. Second, the derivatives market is characterized by strong innovative product development and diversity. Practical problems, notably computing capacity, however, prevent the representation of all that diversity in the model, even though it would have been perfectly possible in principle. Note that the entire derivatives market consists of a computerized network of trading in mathematical algorithms with ad hoc human interaction. Even though the actual simulation runs for this paper are based on a fairly primitive model of trade in the stock and options markets (see Taymaz, 1999) the interpretations of the experiments have to be preceded by a broad-brush presentation of the derivatives market to place what we have done quantitatively in a relevant theoretical context.
2. Economic dynamics – the experimentally organized economy
Economic dynamics is synonymous with concurrent and endogenous institutional and organizational change and the employment of a dominant tacit competence capital in production (Eliasson, 1990a, Eliasson, 1996a; Eliasson, 1996b). To capture that in theory we briefly introduce the notion of a Knowledge Based Information Economy (Eliasson, 1990b) to clarify the assumptions of the Experimentally Organized Economy (EOE, Eliasson, 1987, Eliasson, 1991a), and that our analysis is predicated on a state space, or a business opportunities space, that is enormous and only fractionally (and differently) known to each agent in the market. This establishes an enormous potential for productivity advance at higher levels of aggregation through recombining factors of production and reallocating resources (see Carlsson, 1991; Eliasson, 1998b; Eliasson and Taymaz, 2000 for empirical evidence). It also introduces an economic environment which to each actor is largely unknown when viewed from any point in state space. Since each actor views its local environment through its own interpretation filter it is apt to be both grossly ignorant, and significantly misinformed about circumstances that may jeopardize its very survival as a market agent. The investment process of each actor is therefore likely to be a path strewn with more or less serious business mistakes and occasional winners. Hence, the way markets of the Experimentally Organized Economy (EOE) are organized for efficient experimental selection becomes the important determinant of long term economy wide evolution. We deal with the problem of efficient selection in the EOE in terms of Competence Bloc Theory (Eliasson, 2000b; Eliasson and Eliasson, 1996; Eliasson and Eliasson, 2000).
Organizational change occasioned by innovative financial markets engineered by new C&C technology is thus a main theme of this paper. Because institutional and organizational change determines how new technology is introduced in the economy, we need a market and agent based model capable of representing that dynamic. The theory of the EOE and the MOSES model offer that.
2.1. The theory of the Experimentally Organized Economy (EOE)
The theory of the EOE is presented as the antithesis of the Walras – Arrow – Debreu (WAD) model. The notion of a knowledge based information economy provides some necessary prior modifications of the WAD model, notably about the state space. Competence bloc theory explains the market selection of projects within the vast state space, or business opportunities space of the EOE.3
In the EOE
free competitive entry (Item 1 in Table 1) into, and exploration of the opportunities space, keep incumbent agents under competitive pressure to perform. Incumbent firms respond by reorganizing and/or rationalizing (Items 2 and 3) upgrading their productivities. They are all under constant threat of being competed down along a Salter (1960) performance curve, or out of business (item 4). Because of competition and selection aggregate productivity performance increases.
choices of market and technology determine the fate of the individual agent, which often fails. But choices must be prematurely made to avoid ultimate failure and exit, and hence cannot be avoided. Business mistakes become a normal cost for economic development.
The four mechanisms of schumpeterian creative destruction and economic growth
| 1. Entrepreneurial competition (entry) enforces |
| 2. Reorganization of incumbent agents and/or |
| 3. Rationalization, or |
| 4. Death (exit) |
-
Source: Eliasson (1993) and Eliasson (1996a).
A break down of economic systems effects
| 1. Rationalization of information processing given the manufacturing and distribution structure (“doing the same thing but faster”) |
| 2. Reorganizing information and communications flows, given manufacturing and distribution structures (e.g. through ”speeding up inventory turnover”) |
| 3. Optimizing manufacturing and distribution flows over a given structure |
| 4. Reorganizing physical flows to exploit information and communications technology (dynamic systems effects) |
| 5. Simultaneous reorganization of physical and information and communications flows (Integrated production) |
-
Source: (Eliasson, 1996c).
Having said that we have also introduced the four fundamental growth generating mechanism in the EOE that are coded into the MOSES model, or what we call the four elements of Schumpeterian Creative Destruction of Table 1. They are universal (Eliasson, 1996a), since all four categories can be defined and observed at all levels of aggregation, even within the firm.4
2.2. A generalized Salter curve analysis of innovation enforced by fear of competition
Using the concept of a Salter curve to describe the dynamics of the EOE we can (1) decompose economic growth into the four investment categories of Tables 1 and 2 illustrate the huge synergistic productivity improvements that can be achieved at all levels of aggregation through "organizational change" as illustrated in Table 2. This amounts to classifying firms into growing, contracting, and exiting agents, together shifting the Salter curves in Figure 1 out- and upwards. The main point made is that the large effects of C&C technology are systemic through reorganization of both information processing and physical production (item 5) and that the realization of these systemic effects requires considerable management organizational competence within the firm. At higher levels of reorganization among firms as in Table 1 this, as we have already concluded, becomes a matter of how markets and competition work.5
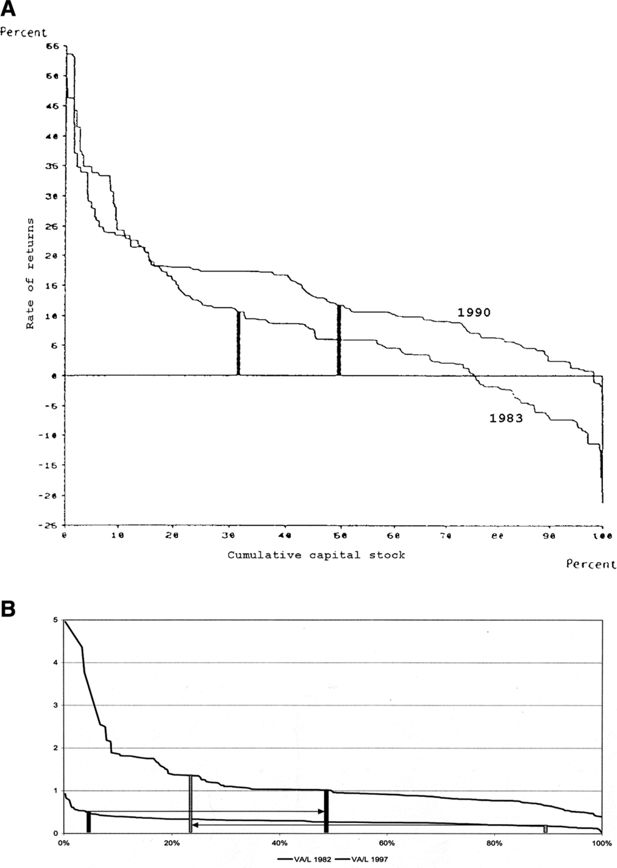
A) A Salter Ranking of Rates of Return to Capital in Swedish Manufacturing 1983 and 1990. Note: The figure ranks nominal rates of return over the nominal market interest rate across Swedish manufacturing firms 1983 and 1990. The vertical columns show the position of the same firm each year. The width of the column measures the size of the capital of the firm in percent of that for all manufacturing. Its rate of return has increased between 1983 and 1990, but it has lost in ranking. Its relative size has increased between 1983 and 1990. Source: Eliasson (1991a) and Albrecht et al. (1992): Moses Database.
The initial state description of the MOSES model economy consists of several performance distributions (Salter curves) over firms. The labor productivity and profitability distributions in Figure 1 of real initial data sets for the years 1983 and 1990 illustrate. The horizontal axis measures performance (labor productivity in Figure 1B) in descending order to the right, each step or column representing one firm, its size being expressed in percent (of total capital stock) of the entire population of firms.
In the ranking of Figure 1 each firm is challenged by superior firms to its left, with a greater capacity to outbid itself in both product and labor markets and perhaps also in financial markets to obtain funds to invest and become more profitable. This firm therefore has to (Eliasson, 1996a) take innovative counter action to prevent being overtaken by competition. But the superior firm to the left also knows that firms on its right may be preparing strategic counter action, to leap frog its performance disadvantage by risky innovation and consequently also has to take action to offset that risk. In an open market economy each firm along the Salter ranking finds itself in such a more or less precarious competitive situation. And this is not all.
In the wings of the market theatre eager challengers wait for an opportunity to enter the scene, and if allowed ("free entry") will do it any time. Entrepreneurial entrants are not only optimistic and eager to enter the market fray. Even though on the average less productive than incumbents the group often includes some super performers. So free entry is a real threat to incumbents (Eliasson, 1991b). In principle therefore all agents in an open economy find themselves more or less under competitive threat to innovate themselves out of a perceived precarious position. This "innovation pushed by fear" is sufficient to keep the Schumpeterian creative destruction process of Table 1 in perpetual motion (Eliasson, 1995b), and it is modelled as an endogenous competitive process by the entry algorithms of the MOSES model. But the economy wide outcome of that process depends on the character of the innovation response, incentives in markets and the efficiency of project selection and scale up in markets.
2.3. Competence bloc theory governs the efficiency of project selection
With competitive market selection of business experiments being the main vehicle for economic growth, the main concern of policy makers concerned with growth should be how these markets are organized for dynamically efficient selection. This means making sure that the minimum of market agents being in place to minimize the negative economic incidence of (1) keeping losers on the books for too long (Economic mistake Type I) and of (2) terminating winners prematurely (Economic mistake Type II). What is needed as a minimum for such dynamically efficient project selection is explained by competence bloc theory (Eliasson and Eliasson, 1996; Eliasson, 2000b). (Before we go on it must be understood that the agents of the competence bloc can in principle be found in both the market and internally within the business hierarchy of a large firm. Since we do not yet model project selection within the firm in the context of the MOSES model that observation need not concern us here).
The competence bloc is not yet introduced in the MOSES model. Hence it will not make sense to present it in full here. For that the reader is referred to the references above. Suffice it to mention that completeness of the competence bloc is one criterion for efficient selection. The completeness of the competence bloc defines the incentives for innovation and entrepreneurship and for new entry in particular. New entry in turn initiates competition, that forces incumbent agents to innovate (previous section) and enforces the Schumpeterian creative destruction of Table 1, and the selection that drives economic growth. For incentives to be credible, institutions that reduce the uncertainty surrounding the (property) rights to the expected present value of investments today as valued in financial markets must be in place (Eliasson, 1998a).
3. The MOSES model economy
The MOSES model economy approximates the theory of the Experimentally Organized Economy (EOE. Eliasson, 1987; Eliasson, 1991a) which exhibits dynamic properties of a kind that are not to be found in mainstream general equilibrium modelling. Surprisingly, neither have we found much of the typical non- linear selection based, and initial state dependent economy wide cumulation phenomena that go under the name of "deterministic chaos" (Day, 1983) in the growing but fragmented evolutionary modelling literature.6 The principal differences concern the economy wide cumulative consequences originating in different outcomes of market agent selection and the consequent market self-coordination of the entire MOSES model economy. One basic assumption is particularly important; the size and complexity of the state space, or the business opportunities space,7 which is "sufficiently enormous" to make all actors ignorant about circumstances that may threaten their very survival, and prone to commit systematic economic mistakes.8 As a consequence, production structures in the MOSES model are in a constant flux. Endogenous investment of firms and an endogenous population of firms through entry and exit explains most of this. Endogenous production structures remove all static equilibrium properties from the MOSES model, reduce the information content of (endogenous) market prices and (because of their heterogeneity and "non atomic size") give agents considerable price setting autonomy. In that sense MOSES becomes an economy wide model of general monopolistic competition (Eliasson, 1985). Given our previous discussion and our interest in growth modelling we can also call MOSES a generalized economy wide Salter (1960) analysis of economic growth.
For the economy wide financial market analyses to follow the following type of market agents in MOSES will be of particular interest:
– The (production) firms
– The actors in financial markets
– Intermediaries between the financial and the real production system
Financial assets are defined by pricing algorithms, and thereby also assigned a property right. They therefore also become tradable (Eliasson, 2000a). This specification is not so difficult for physical goods and services, but to define future profits from investments today as accessible property requires new legal foundations that have only recently been developed (Eliasson, 1993). The present value formula is a value approximation to that abstraction defined under the equilibrium assumptions of the WAD model (Eliasson, 2000a).9 Trade in that abstraction requires support by a register of units (certificates) that regulates access to and the rights to the profit flow. The stock certificate is one such abstraction. It took a long time for the legal rules of the stock market to be established and for trade in those certificates to be possible.
Complexity increases many times over when we introduce trade in future transfers of ownerships stocks (options), but the principles are the same. In the regular stock market prices are affected when managers rebalance their portfolios to minimize risks and maximize expected returns. The pricing of options is therefore affected by actual trades in stocks, but stock prices are also influenced by trades in options. How traders meet becomes a complicated story. For the time being we use a simple random pairing device to make traders in both markets meet.10 For more detail see Taymaz (1999).
3.1. An evolutionary model of the experimentally organized economy – a brief presentation of MOSES11
The main micro agent of the MOSES model is the firm, and endogenous entering and exiting firms keep the markets of the model economy "alive". The firm population is therefore endogenous through market selection, and firms come in different sizes and structures and with different profit seeking agendas. Aggregation is explicit over dynamic markets governed by competing agents with autonomous price setting capacity, up to the level of a national economy. Behavior is mainly deterministic. Selection makes the MOSES model highly non linear and initial state dependent, exhibiting therefore now and then typical "chaotic" characteristics. The statistical resolution of the model is set at the firm or division level and the endogenization of growth should be seen as dependent upon market selection among those entities as they are kept in competitive motion bin the Schumpeterian creative destruction process of Table 1.
3.1.1. Specification – overview
The MOSES model when seen from a "high altitude" comes out as a Leontief – Keynesian 11- sector model where manufacturing has been divided up in four markets (product, labor and financial) in which firms, compete for customers, workers and financial resources. MOSES agents face convex production sets,12 that are however constantly shifted outwards because of entrepreneurial entry, investment and competition among firms as illustrated with the Salter curve analysis above. New best practice global technology is brought in by firms’ endogenous investments. Growth thus becomes endogenized under an exogenous global technology constraint.
The individual firm is modelled on the format of a business planning and decision system as observed in the interview study. Case studies have thus been the source of tailoring the individual firm model Eliasson (1976a). The model runs on a data base of 150 real firms, data on which has been collected in an annual special survey (The Planning Survey, Albrecht et al., 1992) by the Federation of Swedish Industries, that defines the initial state of model simulations. There are about 75 additional “synthetic” firms introduced the initial year to make up the difference between the market aggregate of the Planning Survey firms and the corresponding aggregate from National (accounts) statistics. To achieve stock and flow consistency between these statistical sources, based on different taxonomic principles, constitutes a major statistical effort (as described for 1982 in Albrecht et al., 1992).
Case studies have been constantly carried out to improve specifications of firm behavior and market processes. Researchers at the Industrial Institute for Economic and Social Research ( IUI) in Stockholm, where the full model was put together and calibrated, and Swedish public committees were often interested in gauging the macroeconomic consequences of micro circumstances studied in special inquiries. MOSES could therefore often be upgraded on the budgets of other projects. One example was the joint IUI and Academy of Engineering Sciences (IVA) project of the state of technology of Swedish manufacturing industry, which provided historic data on the best practice technologies for the four MOSES subindustries (Carlsson et al., 1979; Carlsson, 1991). Another imprtant example was the economy wide MOSES based cost benefit evaluation of the Swedish industrial support program for crisis industries in the 1970s/1980s (Carlsson, 1983). The Government Agency for Civilian Catastrophe Preparedness (ÖCB) paid for the inclusion of a new and fifth IT industry13 in the MOSES model (Eliasson and Johansson, 1999). Last, and not least, this project on financial markets14 is being funded be the Swedish Transport and Communications Board as part of a larger inquiry of the role of C&C technology in Swedish economic development.
3.1.2. The firm model
The firm is modelled in MOSES on the format of a business planning system as observed in the interview study Eliasson (1976a), which concludes in chapter XI with a sketch of a theory of the firm. Firms are governed by profit targeting algorithms that make them climb ex ante perceived profit hills. This targeting approximates ex ante long term profit or wealth maximization. Since these profit hills constantly change because of all the competitive profit hill climbing going on firms constantly fail to attain their profit targets and must revise their expectations and plans from period (quarter) to period.
The MOSES model is comprehensive and economy wide in the sense that all relevant Keynesian demand and mistaken firm expectations feed backs are at work. We have recently devoted considerable attention to representing the allocation of resources over financial markets, and to how these mechanism are influenced by C&C technologies (Eliasson, 1995a; Eliasson and Wihlborg, 1998; Eliasson and Taymaz, 2000). This means that the model has to be completely stock flow consistent at the firm level and through all accounts up to macro over time. The model furthermore features endogenous price and quantity determination in markets but that inconsistencies between individual firm plans mean that markets never clear.
3.1.3. Schumpeterian creative destruction
For the empirical presentation to follow, it must be understood that economic growth in the model is endogenous and occurs through the four investment mechanisms of the Schumpeterian creative destruction process, which is moved by entrepreneurial entry competition as shown in Table 1. Depending on circumstances, firms both expand and contract operations in response to competitive challenges. One can also say that growth occurs through competitive selection (Eliasson, 1996b). It therefore becomes necessary to explain how (1) selection is governed , how (2) incentives to enter markets and commercialize new technology are created, and (3) how such entrepreneurial competition forces incumbents to innovate to leap frog expected competition and/or to avoid being competed down the Salter curves in Figure 1, or even out of the market (exit). The first aspect is accounted for by competence bloc theory (Eliasson and Eliasson, 1996). The second and third, that are critical for entrepreneurial entry, have been discussed under section 2.2 above.
The MOSES model is fundamentally deterministic, and market governed selection makes it highly non linear and initial state dependent. It hence generates output that appears "random" and now and then exhibits phases of chaotic behavior ("deterministic chaos") that is mathematically related to stochastic number generation (Carleson, 1991). For practical purposes, however, four market mechanism in MOSES have had to be (temporarily) made partly stochastic. They are:
Direction of search for workers in the labor market, or as this mechanism can also be interpreted: Information about workers being willing to change jobs is made stochastically available to recruiting firms (Eliasson, 1976b).
The degree of success of R&D investment outcomes, thus allocating winners and losers on individual firms (Carlsson, 1997).15
The rate of entry each period is a stochastic function of the excess returns to capital over the interest rate registered in the market. New firm characteristics are drawings from an empirical distribution (see further below).
A particularly important decision variable is expected excess profitability over the current long-term interest rate. Firms' borrowing and investment spending decisions are dependent on expercted excess profits so defined. Realized excess profits govern firms production planning, recruiting and willingness to offer wage increases (see Eliasson, 1976b).16 The rate of firm entry is dependent on the same profit variable among incumbent firms in each market. The labor and capital productivities of new investments in firms are drawn from an exogenous (global) pool of best practice technologies. Individual firm R&D investments (after Ballot and Taymaz, 1998) raise the probability of the firm of scoring a winning technology with superior productivity characteristics compared to those in the exogenous pool (Item 2 in the list above).17 The new productivity vintages are then integrated with the existing capital equipment of the firm (see Eliasson, 1991a). The productivity characteristics of new entrants are drawings from a similar empirical distribution (Item 4 above), only that the spread is much wider. For practical measurement reasons the MOSES model runs on well-defined observation units (firms or divisions) that either enter or exit or grow or shrink through their endogenous production, rercruiting and investment decisions. In the economy wide perspective of the micro to macro model reorganization (Item 2 in Table 1), hence, can be interpreted as both limited to internal firm reorganization and reorganization among firms through selection. So far, we have not had the time to generalize the firm model to accounting also for internal reorganizations even though it would have been good to have such a feature in this context of financial market analysis, for instance to understand the economy wide importance of having or not having viable markets for mergers and acquisitions (M&A). See further Eliasson (1998b, Eliasson (2000a) and Eliasson and Eliasson (2000).18
Firms in the MOSES model interpret their market environments through adaptive smoothing algorithms in which projections are upgraded because of past mistakes ("learning") and corrected for risk aversion (Eliasson, 1976b; Eliasson, 1980; Eliasson, 1991a). The entire MOSES model economy "learns" from selection by way of the Schumpeterian creative destruction and selection process of Table 1 (Eliasson, 1992a; Eliasson, 1992b; Eliasson, 1996b).
3.1.4. Households as consumers, savers, and private wealth managers
Households are modeled in macro in MOSES. As has become traditional in macro economic modelling individuals/households are thought of as identical ("representative") and infinitely small ("atomic"). Under such conditions rational utility maximizing households can be represented in macro as a Stone type expenditure system. All income paid out by producers are fed back as demand to markets after having been filtered through the Swedish tax and income transfer system (Eliasson, 1980). The representative household is modelled as a sophisticated consumer, saver, investor and borrower under a Modigliani and Brumberg (1955) life cycle and a Friedman (1957) permanent income consumption perspective. We have even been playing around with an extended household governance principle in that the household "principals" are not aiming to run the wealth at the expected life cycle horizon of each household member down to zero, but rather aim for continued growth of the real wealth of the extended household growing for ever (Eliasson, 1976b; Eliasson, 1982; Eliasson, 1985). We mention this because this study will represent wealthy households as investors in financial assets. In that capacity they will temporarily be separated from the aggregate household system as individual portfolio holders who interact with the aggregate through income and borrowing flows.
3.2. Calibration
The MOSES model is empirical in that its specification, notably the firm model has been based on careful case studies (Eliasson, 1976a), its initial state measured annually since 1975 on a separate survey (the Planning Survey) of the Federation of Swedish Industries (Albrecht et al., 1992; Taymaz, 1992b), and all being placed for chosen initial years within a stock flow consistent complete micro to macro Swedish National Accounting framework. The latter accounting system has required a major statistical effort, since public sector data have had to be reclassified on the market taxonomy firms use in their internal statistical system, from the production taxonomy of public statistics,19 ,and in initial state dependent non linear selection based models like MOSES eerrors of measurement tend to cumulate (for 1982, see Taymaz, 1992a). The manufacturers of the model have then been calibrated against Swedish macro data and distributional characteristics, for instance the Salter curves of Figure 1, first using the ad hoc method described in Eliasson and Olavi (1978), then the unique computerized calibration method developed by Taymaz (1991b). We have taken the empirical credibility of MOSES seriously. Even though we believe we have got the specification, the statistical measurements and the calibrated parameters right we talk about MOSES as representing a Sweden like industrial economy, which is sufficient for making simulation experiments empirically interesting.
All simulation experiments reported on in this paper use the parameter set calibrated against historic Swedish test variables for the period 1982 -1990.
It should be emphasized that well researched empirically relevant specification combined with detailed measurement has to a significant extent relieved us of a number of parameter estimation problems. This is one of the many advantages of the micro simulation method.
Quantitative control of economy wide dynamics has been particularly difficult. This includes calibrating parameters such that an empirically reasonable endogenous growth cycle emerges. About a dozen parameters regulating agents’ behavior across markets and over time, notably those relating to the Stockholm School ex ante plan ex post outcome feedbacks, are critical for economy wide systems dynamics. These are also the market mechanims that make the MOSES model depart fundamentally from general equilibrium type models of Walras-Arrow-Debreu (WAD) descent.
3.3. Generalizing from cases to macro
The MOSES model endogenizes aggregation over dynamic markets under non- price taking conditions and is market self-coordinated without a need for an exogenous Walrasian auctioneer. It is therefore the ideal tool for analyzing the economy wide long-term consequences of events occurring at the micro level, such as market interactions between firms, or organizational changes within firms and divisions. The model has also been used frequently to generalize from case studies to macro, under the assumption that its parameters reasonably well represent the dynamic market aggregation of consequences up to macro. Dynamic cost benefit analyses of major investment programs would be one example, for instance technical spillovers from the Swedish fighter aircraft Gripen (Eliasson, 1995a). The synergistic economy wide productivity effects of the introduction of generic new technologies, such as C&C technologies and the Internet is another case, as are the consequences of C&C technology for both new product development in, and for raising the allocational capacities of financial markets that we will study in the following section of this paper (Eliasson and Johansson, 1999; Eliasson and Wihlborg, 1998). Only a model of general monopolistic competition, like MOSES, can be used for such purposes.20
4. Theoretical product development for emerging financial markets- modern financial economics as an intellectual new product innovation
Few industries are truly science founded. IT industry is not. Biotech industry is. It has been based directly on Watson & Crick’s discovery of the genetic code, and three path establishing methodological break throughs based on it around 1975, one of them receiving the Nobel Prize (Eliasson and Eliasson, 2000). The perhaps most science founded industry however, with by far more profound economy wide consequences is the new market for financial derivatives. These markets are based on a sequence of developments in mathematical economics, all based on the Walras-Arrow-Debreu (WAD) platform, beginning in the 1950s, all surviving originators having been awarded the ("Nobel") Prize in economics.21 This offers a unique possibility to study the consequences of introducing new market information devices and financial products optimized for a WAD type static equilibrium economy in the radically different market environment of the MOSES model economy. Since these mathematical product abstractions have in fact been traded in the markets of real economies, notably in the US, there is some empirical evidence to compare with MOSES simulation results.
4.1. New innovative products developed in the ivory towers
Well through the 1950s financial economics was almost all a matter of empirically based rules of thumb in firm decision making. In this subfield of business administration theory business practice encoded as rules of thumb dominated over systematic and consistent analysis. This field was suddenly broken up by the successive entry of new, innovative intellectual tools of analysis based on the WAD tradition and optimized for that same economic environment, a disruption of the entire field of business administration that has gradually moved financial analysis away from business administration practices into the abstractions of economic theory.
It began as an engineering product development by (Markowitz, 1952) who formulated the theory of portfolio choice , a path breaking new financial product that since then has radically changed ways of thinking among financial asset managers. Next, Franco Modigliani and Merton Miller (1958) demonstrated theoretically that large parts of the flora of rules of thumb would be made irrelevant if it could be assumed that financial risks could be separated from other financial considerations and traded in separate markets for risks. This theoretical "insight" generated a mounting controversy in academe and in the financial community. Above all the famous Fisher separability proposition was questioned. It stated that decisions in real product markets and financial markets could be kept separate. Already here those new abstractions clashed with the economics of MOSES firms in that price expectations in product, labour and financial markets are integrated in the business plans of individual firms, plans that are then from period to period tested against each other "for consistency" in markets, revised and then tested again. Another point of criticism was that financial transactions costs in the new theory were assumed to be zero. None of this is true in the MOSES economy, so we have an interesting "empirical" problem to address below in that (1) financial and real markets are explicitly integrated by management in the business plans of MOSES firms, and (2) that business mistakes of types I and II (see Section 2.3) become market transactions costs with fundamental economy wide consequences.
The next round in financial product development occurred when William Sharpe (Sharpe, 1964) introduced the Capital Asset Pricing (CAP) model and demonstrated how risks could be systematically and rationally (under the WAD assumptions) priced and then traded in separate markets. The CAP formulae established tradability and constituted a theoretical underpinning of the rapid development of new markets in risks that in fact soon took place. In the CAP algorithm estimated beta values indicate the individual contributions of shares to the risk exposure of the entire portfolio, and therefore also prices.
The next phase in financial product development soon arrived with the algorithms for options pricing developed by Black and Scholes (1973), which made the markets for financial derivatives a practical reality. In a couple of decades the B-S/M options pricing formula had made such markets a dominant reality, not only refashioning national and global financial systems, but also the global economy, and in passing presenting national policy makers with a much more restricted agenda of political choices than before.
The Black-Scholes/Merton algorithms tell how an option should be valued for each given level of risk. Hence the derivatives market can be used to reduce financial risks through reallocating risks over markets to those traders who are most competent to understand the risks.
Before we go on it should be recalled that the MOSES model, much as academic finance before its scientific revolution in the 1950s, was built bottom up on observations of business practices and rules of thumb decision making, as studied in Eliasson (1976a), and then conded in Eliasson (1976b). It still remains that way. To be noted also is that when those observed practices are integrated this whole economy wide market model comes out not only incompatible with the fundamentals of neocclassical or neo walrasian equilibrium orthodoxy (Eliasson, 1985; Eliasson, 1991a; Eliasson, 1991b; Eliasson, 1992a), but the rules of thumb and information proxies used in business practice, suddenly appear very much rationally founded when viewed as they should as ex asnte expectationally founded - the Stockholm School connection. Once ex ante plans are confronted in markets and ex post sorted out he world of economics appears quite different. Since the fundamentals of modern financial economics occupy a very special corner of the MOSES economic system, it would in fact the very interesrting, now that this new monetary/ financial part has been integrated within the model, to test the reliability of the new decision rules introduced, for instance the Capital Asset Pricing Model (CAPM) of Sharpe 1964, in the artificial economic world of the MOSES economy.
One could finally say, using Rybsczynski’s (1993) categorization mentioned above that introducing (in this paper) portfolio choice moved the financial system of the MOSES model from a bank- oriented system to a (capital) market oriented system. Introducing the CAP and B-S/M options pricing formula introduced the securitized financial system.
4.2. Introducing an innovative financial services industry in the MOSES model
Financial products are introduced in the MOSES model economy in seven steps:
Step I: A market valuation of net worth of individual firms, efficient market type and the possibility for (only) households and specialized investment firms to hold portfolios
Step II: Portfolio holders also include manufacturing firms that can:
– repurchase own stock (in own firm)
– buy shares in other firms
These investors can buy stock, sell stock, pay back debt or invest , and deposit money in the bank at the offered interest rate.
Step III: A market valuation of debt equity ratios that determine individual firm interest rates
Step IV: Firm financing through stock issues
Step V: Options and derivatives
Step VI: Wealthy individuals can become industrially experienced venture capitalists.22
Venture capitalists can build industrial experience from learning from their own experience of investing, and thus acquire a unique understanding of innovative projects that lowers their risk. This will be done through introducing a competence block module (Eliasson and Eliasson, 1996; Eliasson, 2000b) in the MOSES model. By formulating pricing algorithms for the financial products we establish tradability in those products.
Step VII: Insiders and outsiders in the stock market.23
Insiders will be defined as both particularly well informed individuals, who happen to (1) know before the market about an imminent occurrence that will affect the price of the stock, and (2) who have the industrial competence to understand the commercial opportunities associated with particular technologies. The second type of industrial competence is what make venture capitalists competent. Modelling that competence draws on the genetic learning mechanisms introduced in MOSES by Ballot and Taymaz (1998). In fact, learning and diffusion of knowledge through venture capital and insider activity will create in MOSES the type of positive externalities that are associated with new growth theory. An interesting question that we will come back to later is whether more efficient financial markets, because of new financial products, will reinforce these positive externalities, or not.
4.3. Introducing the efficient stock market
We introduce a simple stock market in MOSES and superimpose investment companies that manage their portfolios and then engage in derivatives trading in stock options, or algorithms representing their perceived future value.
The value of the firm to the owners of its equity has earlier been represented by its replacement value, or total assets replacement valued minus nominal debt, as described in Eliasson (1992b), Eliasson (2000a). We now allow for market valuations of that equity using different market pricing formula as follows:
Insiders use internal profit projections in firms to derive the present value of future expected profits.
where Rⁿ is the current or expected nominal rate of return on replacement valued net worth and δᵢ the insider’s discount rate (see Eliasson, 1996a).
Outsiders use dividend projections to determine the firms value according to the standard dividend valuation formula:
We make outsiders rather simple minded and expect them to believe in a rational expectations (efficient market) type valuation formula:24
which is (by Gordon’s formula) the sum of all discounted future dividends, assuming static WAD type expectations. δ₂ is the outsider’s discount rate. DDIV stands for the rate of change in dividends (DIV). The outsiders have more difficulties assessing the dividend income stream than insiders. Hence, in general
Differences between insider and outsider valuations occur because of (1) uncertainties relating to the fundamentals behind dividend policies, and (2) different risk premia in the discount factor.
We specify an initial distribution of shares over portfolio holders who act individually in the stock market. They however mix with the aggregate when it comes to consumption spending. Initially we create shares with an arbitrary nominal value of 1000 SEK. (The number of shares then becomes the initial value of net worth divided by that nominal value).
Firms can issue new shares to finance expansion. The firm does so (1) when its investment plan must be reduced because its borrowing has driven up its interest rate, but (2) its effective rate of return on its shares (ER) is still larger than its borrowing rate i:
The effective rate of return is defined as:
ΔMV/MV + DIV/MV is the rate of growth in the market value (MV) of the firm (see below) plus is the rate of dividend payout of that market value or DIV/MV. If (Equation 4) holds the market is willing to pay a positive premium to the incumbent shareholders.
Holders of stock are of four kinds:
Outsiders; Wealthy people invest in non-liquid holdings in stock rather than deposit them in the bank. Outsiders are solely concerned with dividends. They rarely change the composition of their portfolio through speculative purchases and sales.
Professionals/speculators analyze external firm data. The pure speculator only looks at stock prices (Taymaz, 1999). Professional speculators may however use a variety of analytical devices. They may obtain information on profits and the balance sheet, but with a delay compared to the insider. They compare firm profits and firm dividends and consider dividends as predictors of future profits. The better the historic fits the more confidence they place on the projections. Unexplained variations enter the discount factor as a risk premium.
Most actors in MOSES financial markets are hybrids of outsiders and professional speculators. They convert dividends into stock prices using (Equation 2) and (Equation 3) and compute weighted averages, the weights telling how speculative they are.
Professional speculators will be specified to be (sometimes) superior investors compared to insiders because of their superior understanding of the macro economy.
Insiders know everything about their own firm (all that is in the MOSES data base). They act as professional outsiders when they buy shares in other firms.
Firms act as professional outsiders when they buy stock in other firms, and as insiders when they buy back their own stock. This means that firms only figure in MOSES as arm’s length investors in other firms, and do not acquire firms strategically.
Insiders (in other firms) and professional outsiders evaluate the dividend behavior of each firm over the past in terms of observed profitability and dividend behavior. The better the fits, the more confident they are in their dividend evaluation algorithms as proxies for profits and future stock prices. Deviations enter as an extra risk premium in their discount factor. But the professionals may also worry about the ability of managers/insiders to assess the external profit situation of their own firm. They therefore consult outside experts for predictions. Here we can use the method of Antonov and Trofimov (1993), who introduced outside experts/consultants in the MOSES economy to help firms understand what was going on in the model economy. Their two "statistical bureaus" each used their favorite theory (a Keynesian and a neoclassical model) to predict. In their two central planning scenarios firm management had to build their plan on the predictions of one of the two. In a third free market scenario they were allowed to rely on any of the two or any correlation they happened to believe in. The point is that the outsider and insider evaluations of stocks or stock options can be based on a variety of principles.
Both insiders and outsiders need price and market (sales) forecasts. Insiders feed them into their own firm model as expectations, and normally use the forecasts of their own firm. Therefore, insiders may also be wrong, since outsiders (because of superior competence or chance) may have a better understanding of the macro economy.
Outsiders use a simple model to predict firm profit margins, for instance:
Where P and W are firm prices and wages respectively and D are operators that stands for relative change in the same variables. Hence, they can compute the nominal rate of return Rⁿ in (1), using externally available balance sheet data and the definition:
assuming S/K to be roughly constant.
M stands for the gross profit margin of sales (S) and ρ is the depreciation rate on capital K. The firm value can then be computed using (Equation 1).
Professionals and insiders are bold speculators. They buy and sell according to their analyses but revise their assessments every quarter to buy and sell again according to their revised assessments. This is in principle quite like computerized trading already being practiced in the market. To get leverage on such speculative activity we introduce term contracts and options.
Every professional trader should in principle be willing to offer term contracts and options based on their expectations. If expectations among traders are very varied, they should have a stabilizing influence on market pricing. If they are first very differentiated and then suddenly shift uniformly in one direction (which can easily be engineered in the model) very interesting macro behavior will erupt.
To increase the leverage even further professional traders may be allowed to borrow. They borrow as firms do, and pay an interest rate that depends positively on the correlation between the debt market value ratio of their portfolios. If market values drop suddenly and interest rates shoot up on highly leveraged portfolios interesting market behavior should be released.
Now what can we do with this?
With highly leveraged professional traders in both spot and futures markets uniform changes in expectations should cause significant reallocations of funds between firms, traders and the bank of the MOSES model if local interest rates shoot up and firms’ borrowing capacity is affected. Since the banking system can create money, credit available for investment will also be affected.
The portfolio investment possibility of individual firms introduces one additional potentially important allocator of resources through the entry and exit process. A firm’s net worth is defined as:
Where K₁ stands for hardware production capital, K₂ is the portfolio of financial assets, and K₃ current trading assets including inventories of inputs and own products. Now let
where ST is investments in shares that are allowed up to a share ẫ of the portfolio of financial assets, then
When a firm expects a better return on investing in other firms’ shares than in its own production ST investments increase and appear in the balance sheet at current market values. Since the firm may make investment mistakes in its financial portfolio it becomes perfectly possible that a highly leveraged (high D/NW) firm with large investments in ST, after a stock market slump may find itself in a bankruptcy situation with a NW ≤ 0. This situation may thus be entirely unrelated to its own manufacturing performance. A previously well managed manufacturing firm with a good profit record may therefore be forced to shut down because of purely financial mistakes.
Stockholders hold portfolios of shares that they compose according to the relative risk-free returns on deposits in the bank.
Cash proceeds from stock sales can be used to buy more shares in other firms, to deposit in the bank or be added to household disposable income. Professional outsiders and firms can borrow to buy more shares. Professional outsiders/borrowers pay an interest that is positively related to their debt equity ratios. We could in fact define a "capitalist class" that holds wealth and lives on capital income. That capitalist class would then coincide with the insider or venture capital definitions (see above).
4.4. Tradability and trading
Tradability in financial asset markets depends on the possibility of linking a property right to the asset (an institutional legal problem, Eliasson, 1993; Eliasson, 2000a) and on formulating an efficient pricing algorithm. This is what the Markowitz – Modigliani – Miller – Sharpe innovative financial product developments have accomplished, and even more so the Black and Scholes (1973) and Merton (1973) options pricing model. Trading, however, must also be identified as individual transactions between a portfolio holder and shares in one firm to determine individual stock prices. Also, the forming of expectations must be explained. Sellers and buyers of individual shares find (through selective search) each other in different ways. Contrary to the product and labor markets in MOSES, where actual bargaining takes place, when it comes to financial assets demand and supply agents find each other stochastically and clinch rational deals. This is explained in Taymaz (1999).
Firms, households, and private wealthy investors choose between investing in their portfolio or depositing in the bank according to expected after-tax and risk relative returns.
4.5. Introducing derivatives and options
Derivatives are modeled as contracts based on agreements about future trading in the stocks as defined above. There are three kinds of derivatives:
Forward/ Future (term contracts)
Options
Swaps (a series of term contracts)
In principle all financial contracts, including shares, can be seen as options. For the time being we will, however, introduce them in the traditional way. The MOSES model recognizes the following contracts.
Term contracts
Professional outsiders and firms (as professional outsiders) are allowed to take forward positions in stocks. With a forward contract the investor offers to buy or sell at a preset price at some future date. This is a commitment. The futures contract differs from the forward contract in that you offer to deliver a financial asset at a preset price at a specific date. If you want to get out of your commitment you must sell the contract in the market.
Options
An option is the same as a term contract, only that you don’t have to buy or sell. You have purchased an option to buy or sell at a preset price at a specific date.
Swaps
A swap means that the financial transaction takes place by way of a third party.
Originally swaps were created to bypass currency regulations. A US firm had dollars and wanted SEK in Sweden. A Swedish firm had SEK but wanted dollars in the US. The Swedish firm was not allowed to buy dollars. Then the Swedish firm arranged through a bank to buy the dollars of the American firm and to pay the American firm in SEK in Sweden. When authorities used regulation to prevent Swedish firms from transferring money out of the country, regulations could be bypassed because of swapping. No direct transfer of currencies occurred. Swapping meant that the outcome for the parties was anyhow the same. Regulators had created a "semi barter" market, forcing parties to resort to more costly transactions forms (swaps).
Swap transactions have of course been possible all the time, only that modern C&C technologies have made the matching of potential trading and swapping partners more efficient and more complete. Today you may not even need a bank to arrange the transfer.
Standard financial transactions in the Swedish currency market aimed at facilitating access and making the market more complete can take place in a similar fashion. We are talking about firms with different access to the capital market because of credit controls, a bad credit rating or simply incompetent financial institutions. A bank may not want to lend to a small firm that it does not understand, or to a firm with a bad credit record. Another firm which understands the firm in need of cash and has a good credit rating may then borrow from the bank and extend a credit to the firm that needs it. Through increasing access this intermediary firm has made the market more complete through a swap. Obviously new C&C technologies will soon subject an incompetent, legally tied down and over bureaucratized commercial banking system to devastating competition if it does not shape up. Microsimulation method is ideal for studying the economy wide consequences of such institutional competition in financial markets. The venture capital market is one example where banks for legal and organizational reasons are great underperformers (Eliasson, 1997).
Swaps can be used to convert bank lending into venture capital. To do that MOSES requires that inter firm borrowing is explicitly modelled which is currently not possible. We may however limit swaps to professional outsiders which would then appear in the market as more competent competitors to the bank in providing venture capital.
Term contracts make it possible to model pluralism or singularity and everything in between. We can generate a bewildered and perhaps stabilizing expectational future, or a single valued future "compressed immediately into today" that may be heavily destabilizing in a dynamic model economy such as MOSES.
4.6. The Black and Scholes (1973) options pricing formula
The Black and Scholes (1973) options pricing formula (also see Bookstaber, 1987) determines the price of an option for a given risk level. It reads:
where
N(d₁) = the probability that a normally distributed random variable will be less or equal to d₁, the option delta.
P = price of stock now
EX = Exercise price of option
PV(EX) = present value of EX, calculated using the risk-free interest rate
t = number of periods to exercise date
σ = standard deviation per period of rate of return on stock. σ² is the security’s return volatility.
The B-S formula thus tells the price of a call option that eliminates profit opportunities from trading.
Suppose no risk is associated with the future security price. Then σ² will be close to 0, and both d₁ and d₂ will become large making N(d₁) and N(d₂) equal to 1. Hence, the price of the call option becomes equal to
or the current price minus the discounted future price. Whenever there is volatility in the market or uncertainty about the future value of the security (σ > 0) you take on a risk in buying an option, and therefore pay a lower price.
because the EX may not be what is expected. Since expectations about the future value of a security vary, or the competence to evaluate risks varies, a rational foundation for a market in options exists. A theoretical note is in place here. Modern financial economics has done away with Knight’s (1921) distinction between uncertainty and calculable risks. The B-S (1983) pricing algorithm assumes calculable risks, as in (7) above. Pricing becomes an insurance or lottery business. The assumption about the N() functions above is however an empirical assumption that may not hold up in reality, and probably not in the MOSES model economy, which does not have the properties of a stationary process which both the B-S algorithms , and rational expectations (RE) models (see above) require. The distinction between uncertainty and calculable risks has a meaning in MOSES. Our guess is that the N functions are quite unstable over time which should make the Black and Scholes (1973) pricing formula unreliable, a proposition that is perfectly testable through simulations on the MOSES model.
4.7. Stability of fundamentals
Volatility (σ²) can be calculated ex post. In an assumed walrasian lottery setting repeated experiments ("trades") in the options market would then produce calculable risks and predictable outcomes in expectation. If the stochastic functions underlying fundamentals are not stable, as should be expected in MOSES type non - linear environments, then stochastic predictability, being assumed in the B-S pricing formula, may not be there. Thus, using the B-S formula in the non-linear MOSES economy may be highly risky (due to uncertainty), not to say failure prone.
A confused and incomplete, but fast market process may both stabilize and destabilize market fundamentals. If correct in expectation in their perceptions of the external desired economic optimum stochastic equilibrium conditions may be attained. Otherwise, market chaos may be created when the whole army of producers march in the same, but the wrong direction, and market self – coordination fails. We have already seen what happens in the MOSES economy when market transactions are speeded up pushing the entire model economy too close to a market clearing situation that does not exist as an operating domain of the MOSES economy. Near economy wide systems collapse is then the outcome (Eliasson, 1991a). The MOSES model economy, enriched with modern financial services technology, should therefore be able to tell whether the optimum desired by policy makers is an economically desirable target to aim for.
(For instance, you may think you know best about the future. You should then act on that insight, taking a speculative risk, that you do not consider a risk because you know better. This is a commendable entrepreneurial attitude that economies need in large numbers to prosper (Eliasson, 1996a; Eliasson, 1997). The definition of an entrepreneur is that s/he believes in, or understands something no other does and dares to act on that understanding.
A professional trader may be convinced, because of his or her superior understanding of the macro economic situation, that the stock of a particular group of firms will decrease significantly in value. If this belief runs counter to current beliefs in the market, the professional trader goes short, offering to sell stock (that he does not have) at a price below the current price a year from now.
Genetic network learning (Ballot and Taymaz, 1998) in MOSES makes it possible for insiders to know more about the competitive situation of a firm than others. Speculators can search, using genetic algorithms, for correlation patterns in the MOSES economy that have been stable for some time for good or spurious reasons, and when identified, act on them).
4.8. Introducing derivatives
Derivatives are introduced in the MOSES economy in four steps.
First (Step 1) we introduce tradable stock certificates and firms and households as investors in such certificates. Second (Step 2) we make the market value of a firm’s net worth (rather than the replacement accounting value) dependent on the individual firm debt equity ratios that determine a firm’s interest rate. Third (Step 3) we model markets for stocks in which traders determine the market value of individual firm shares. For this step the information and expectations of individual traders must be specified (Taymaz, 1999).
Step 4 introduces the various options defined above, issuers and holders and the markets for such options.
Insider trade is based on superior information or knowledge. Trading insiders therefore make the market more informed. By not being allowed to trade the market will remain uninformed. With insiders trading in the market financial resources will be allocated more efficiently. The MOSES world of an Experimentally Organized Economy distinguishes between insiders happening to know about specific market determining events and insiders being particularly knowledgeable about the business. Prohibiting both insiders from trading may therefore be bad economic policy (Eliasson, 1990a). Instead of outlawing it policy makers can help making markets more complete (read informed) by instituting more speedy disclosure mechanisms, something modern C&C technology is especially suitable for, maybe revealing a trade even before it has been executed, rather than after several weeks of bureaucratic paperwork which was the case in Sweden not long ago.
5. Games and outside participants
The MOSES model constitutes an excellent pedagogical business game, which may be greatly improved when complemented by the sophisticated financial markets of this document. This is especially so because trading in many of the financial instruments just discussed already occurs in markets for computerized trading. This document can therefore be used as an instruction manual for how to set up such a business game.
5.1. Rates of return corrected for risk
The financial investor is concerned with the real rate of return on his or her portfolio, standardized for risks. The higher the estimated risk the higher the return demanded.
We measure the performance of the portfolio by the so-called Sharpe index:
S is the average excess return of the portfolio compared to the standard error of the return (= σ). R stands for the average return, and r for the average "risk free" return (say the interest rate),25 all for the same measurement period. σ can be called a measure of price volatility.
This return over a risk-free investment can be computed for any portfolio. When all investments are in risk - free bonds the Sharpe index is zero. The financial investor wants to maximize the Sharpe index over the longer term. The ex post outcome then depends on his or her ability to foresee the risks taken on. The competence to do that may raise the S even though other, but less competent investors think the risks they have taken on are much higher than they really are.
5.2. Error tracking index
It is of interest to compare the individual Sharpe index with that of a competitive portfolio, for instance that of another portfolio manager or a stock market index. Such a useful error tracking index (T) is:
where R* is the average return on the reference portfolio and σׇָ the standard deviation of the difference between the portfolio return (=R) and the reference return (=R*).
5.3. Volatility
The five inputs in the B-S/M (1973) options pricing formula (Equations 7; 8) are (a) the current price of the (underlying) security (=P), (b) the exercise price of the option (=EX), (c) time of expiration (=t) , (d) the risk free interest (discount) rate and (e) volatility. Since the first four variables can be determined, the expected volatility in the market can be estimated by introducing the market price of the option and then solving for volatility (=σ) to determine the price of the option. Since an estimate of volatility is an input in the Black-Scholes options price it is perfectly possible to define a market for trading in volatility estimates. Then call options traders can outsource the risks associated with predicting volatility in the market, and price the call option according to Equation (7), conditional on that given volatility estimate. Alternatively, s/he may carry the risk on his/her own and use past measures of volatility of the computed variance (= σ²) in actual prices over time, and some econometric model to predict σ, or simply plug in a guess.
To simplify for an outside participant to engage in the options market of the model we can request for each stock an estimate on all current stock and options prices (last period) and a past record of expected and actual volatility (= σ²). The investor can then determine what s/he is willing to pay for a given option or offer to buy options with this exercise price and time to expiration for so and so much.
5.4. Efficient data mining
Any investor in the real economy would assess the future on the basis of what s/he knows, but that is always only a fraction of everything there is to know about. A limited understanding of the whole makes it necessary (for the investor) to invent personal interpretation models ("theories", Eliasson, 1992a) to "understand" what is going on, and those will be different depending on background circumstances, and more or less mistaken. It is possible to prearrange "analytical" data mining devices for participants in the game to support their personal interpretations. These devices may also be made part of the theoretical specification of actors’ behavior. Antonov and Trofimov (1993) have done something like that on the MOSES model. They demonstrated that diverse and seemingly inconsistent behavior of all agents may improve macro-economic growth compared to following mandatory directives/forecasts from a central policy or planning authority supposed to possess superior overview. The reason is that the odd traders discover investment opportunities that those subjected to centrally directed search miss.
One interesting possibility: MOSES exhibits the "chaotic" property typical of non - linear initial state dependent models that some variables may for a long time converge monotonically towards a particular constellation of values, giving the illusion of predictability, only to suddenly "explode" into unexpected gyrations. With such a phase shift any traditional analytic estimate of volatility in the pricing of options by the B-S/M algorithm will be completely misleading, and result in sudden unpredicted wealth transfers between investors. One idea would be to make traders use efficient data mining in the MOSES economy to discover "correlations to trade on". This search could dig deeply into MOSES microstructures relating volatility measures to the interior performance of firms, for instance. If such search for correlations starts from different ends different traders will find different correlations, and belief in those correlations will increase with the number of "confirming" observations (as discussed in statistical learning theory). In a classical general equilibrium environment with costless search and optimum search principles designed for the same equilibrium environment, traders will eventually find a desired equilibrium "point" (Lindh, 1993). If the environment does not have those nice equilibrium properties, such as in MOSES, and if search is not costless, correlations compatible with a different theory, or any "nonsense" correlation (used by "noise traders") will at best be temporarily reliable, but soon guide traders into unexpected and not desired chaotic market circumstances. In a healthy market economy this would now and then be a normal experience for individual traders, and a normal cost for economic development in an Experimentally Organized Economy (EOE, Eliasson, 1991a), but economy wide disaster if a very large number of agents, or central government commit the same mistake. Differential expectations are therefore a market stabilizing element of an EOE. Differential expectations could be created in the MOSES economy in a market game with many outsider investors with different background experiences. .
6. Making markets more complete- how modern C&C technology influences financial markets and the economy at large
New C&C technologies have made financial transactions faster, more integrated and more competitive. If production structures are given and fixed, as well as conveniently convex as in the WAD economy, such technologies would rapidly push the economy towards a "competitive equilibrium". The MOSES economy is however not transparent to financial investors, but complex and mostly unknown. Its structures change endogenously over time, but differently depending on how market competition and the economy evolves. Financial investors possess different understandings of their market environments and entertain diverse beliefs about the future. While this environmental complexity and diversity of insights prevent all actors, including government and the economic analyst, from ever being fully informed, the diversity itself plays a critical role in stabilizing markets and economic development.
Traders and investors may simultaneously be pessimistic and optimistic about the same environmental circumstances, corresponding to different estimates of the volatility in the options formula. The pessimists will prefer to unload their risks, while the optimists may happily take them on. Allen and Gale (1994) argue that if competent traders take on the appropriate risks that they understand the allocation of resources will be more efficient and stock values will increase substantially because risk premia in some traders’ valuation algorithms will be lowered. They quantify this model on US stock data.
It is possible to recreate such situations in MOSES, and the outcomes may be both stabilizing and destabilizing depending on the competence of traders to assess risks. But while this competence may have a well-defined meaning in the rational expectations (RE) framework of a WAD model (see Lindh, 1993) this is not the case in the MOSES model economy where prices and structures depend on each other and change endogenously over time. This underlies the principal question of this study of what will happen to economy wide systems stability when new C&C technologies makes financial markets more complete and faster and derivates leverage up financial market arbitrage. Term contracts add leverage to the trading in risks and increase or decrease stability. Differential expectations can be modelled because of differences in individual experiences and be converted into different risk premia in their discount rates.
6.1. How does C&C technology enter Moses markets
New C&C technologies will increase the speed of financial market arbitrage, make markets more integrated and raise competition (Genberg, 1999). Markets will be more complete in reacting to available information.
Active portfolio management took off with the advent of advanced computing. Financial derivatives are fictious products based on mathematical algorithms. While future contracting was conducted hundreds of years ago, general trade in such contracts had to await the integration of computing and communications technologies in the late 1980s (Eliasson, 1996a).
The 1980s is also the time when the macroeconomic effects of such new financial instruments and trading became statistically visible. A growing political discussion has been concerned with the perceived consequences in the form of limitations on monetary policy and financial regulation caused by more efficient financial markets. Speedy and efficient international financial arbitrage has frequently, since the 1980s, forced reluctant national authorities, unable to close their economies off financially, to change domestic policies, interest rates and exchange rates. Badly managed and corrupt economies in the developing world have been particularly affected.
As far as our understanding of experience from MOSES simulations goes, it is only a matter of time before the limited capacity to pursue autonomous monetary policies will also prevent governments from pursuing autonomous fiscal policies, for instance when it comes to taxes. The hypothesis we venture at this point is that the less potent and the more ambitious as policy maker the government the more error prone its activities (Eliasson and Taymaz, 1992). Understanding and quantifying the indirect economy wide side effects of ambitious policy making on financial market performance, the allocation of resources and long term economic growth is what this paper is about. A market self-coordinated agent based model such as MOSES is needed for such analysis.
6.2. Effects on firms and the real economy
Markets integrate the real and financial parts of the economy. In MOSES firms integrate financial, product and labor market considerations in their business plans. The stock market influences the real economy through (1) the interest rate and investment, (2) the allocation of funds to firms, and (3) the credit multiplier and credit market expansion and contraction.
For firms with shares being traded in the stock market the market value of their equity should be entered in the leverage ratio that determines their (borrowing) rate, which thus becomes negatively dependent on the market value of the firm, which outside lenders can observe. The market value is however dependent both on the firm’s operational performance and on its financial portfolio management. Sudden portfolio losses may put the entire business of a firm in a precarious situation.
If such a precarious situation, caused by financial portfolio losses, or from deteriorating profitability persists, the consequences will eventually result in declining dividends. Dividends can however be temporarily stabilized over time to hide a deteriorating business situation from the outsider investor. The state of information in the market suffers. Overall, higher interest rates and/or lower market valuation of firms will affect its external financing capacity through restricting credits and stock issues.
6.3. Volatility
Variability in the expected prices of an option is called volatility. It affects the estimated price of an option indirectly in the Black-Scholes formula (Equation 8) via the σ factor.26 One may also be interested in the reverse influence, or how variability in options pricing influences interest rates and investments.
Volatility also tells how bankruptcy prone an individual company is. It should affect its individual interest rate and can therefore substitute for the market valued debt equity ratio in the interest determination (Taymaz, 1999). Volatility estimates on historic data according to the Black-Scholes’ formula are indirect. The latter also includes information for the actors in the market on the bankruptcy propensity of the firm. All this is standard economics. The point is that its economy wide consequences can be represented in, and understood through MOSES simulations.
7. MOSES simulation results on options and derivatives
The modular build of the MOSES model makes it not only easy, but also natural to add functionalities without changing its core market structure to overcome at least some of the partial limitations that by necessity afflict all economic models. This also means that new modules can be added without having to reestimate the parameters of the model. Thus, for instance, there are no principal limits to the number of firms/agents, or to customizing their properties if their interfaces with the market remain the same. Market functions are more difficult to add because market considerations are integrated within the business plans and decisions of all individual agents. And the ways agents competing in markets affect macro have been central to the MOSES modelling project.
Two things should therefore be kept in mind when studying the simulation results now to be reported on.
When respecifying the model to encompass not only a credit and a stock market, but to include also trading by different agents in financial derivatives in a securitized financial market, even though only principally and rather simply modelled, the number of market interactions, and hence demands on computer capacity escalated steeply. This meant that we have not been able to run Monte Carlo experiments by varying the stochastic seed (see section 3.1.3 above) to test for robustness of results, as in Eliasson and Taymaz (2000). Hence, until this has been done the results should be regarded as explorative, indicative of new hypotheses, and illustrative of what can be done with the MOSES model.
These technical difficulties, also illustrate a central point of this paper, namely what new C&C technology has done for increasing the degree of sophistication of the financial system, that now spills right into the MOSES model and that to a degree also incorporates code representing what is going on in computerized trading in real financial markets. The markets for derivatives in reality and in the MOSES model are a sophisticated interaction ("trade") in mathematical value determining algorithms between a large number of market agents. Compared to administrative, bureaucratic, and often overregulated industrial bank transactions, and even to (capital) market financing systems, the economywide outcomes of the resource allocations achieved should differ radically.
7.1. General experimental design
All experiments in this study assume foreign relative (export) prices to be exogenous and fluctuating around a steady exponential trend. These price trends and the (also exogenous) foreign interest rate have been set such that firms bringing in best practice globally available exogenous technologies (endogenously through their investments) should be capable by adjusting their wage offers to earn a long term return on the new investment equal to the foreign interest rate. This fairly orderly exogenous global market scenario is, however, complicated in the local Swedish MOSES economy by its initial state that defines numerically how individual firms are positioned at the start of a simulation experiment relative to global markets.27 While the orderly predictable global market environment assumed significantly dampens the resource allocation outcomes of the simulations in ways we did not anticipate when the experiments were designed, the initial state, on the other hand, raises the complexity of interpreting what is happening in the model enormously. Since the MOSES model economy is propelled forward by firms’ price expectations, investments and production plans made up under the upper constraint defined by the globally available best practice technologies its selection based non linear properties tend to make small initial circumstances cumulate long term into very different directions, a common "chaotic" property of such models.28 The economy wide outcomes are leveraged up further by the endogenous population of firms, a unique property of the Moses model economy (Eliasson, 1996b). While the global economic environment can therefore be said to be rather stable and predictable by exogenous assumption, the internal dynamics of the Moses model economy are tremendously more unpredictable.
The experiments (Ex1x2x3x4) have been designed as follows:
Stock/options market:
– No stock market (x1=0)
– Stock market exists (x1=1)
Options market exits (x1= 2)
Interest rates:
– Same for all firms (x2 = 0)
– Firm specific interest rates depend on firms’ debt equity ratio from books (x2 = 1)
– Firm specific dependent on market valued debt equity ratio (x2 = 2)
– Speed of interest adjustment (Taymaz, 1999):
– Slow (x3 = 0)
– Fast (x3 = 1)
Financing through new stock issues:
– Not possible (x4 =0)
– Possible (x4 =1)
The target variable is long term (60 years) GNP growth. As the model is built manufacturing, including the IT industry (Eliasson and Johansson, 1999), is the economic engine that drives growth. In all experiments in this paper tax policies, public sector recruiting, and expansion (Eliasson, 1980) are the same. Comparing GNP levels on the 60-year horizon is therefore synonymous with studying how the introduction of different financial market regimes influence long term growth, everything else the same. Since population growth is exogenous and the same in all experiments GNP level and GNP/capita comparisons are identical.
Experiments with no stock market finance and a general and slow interest determination combination (E0000, E1000 and E0100) represent an industrial bank financing system, dominated by internal finance in firms. Add stock market finance and a fast and individual firm interest determination in (E1211) or (E1111) and we have moved into a capital market financial regime. We can then distinguish between two market regimes; one with only a stock market and portfolio choice (E1211), and the other also featuring a securitized (options) market (E2211).
7.2. Simulation results
We begin by introducing an increasingly more sophisticated financial market regime, then carry out some special inquiries.
7.2.1. Experiments 1 (Industrial banking system)
Table 3 shows GNP levels at the end of a 60 year simulation,29 the number of new firms and exits during the simulation and the population of firms on the horizon.
Outcomes of 60-year experiments
| Experiment | GDP | New firms | Exits | Number of firms on horizon | ||||
|---|---|---|---|---|---|---|---|---|
| E0000 | (7165) | 7164 | (132) | 132 | (93) | 93 | (264) | 264 |
| E0010 | (7922) | 6816 | (126) | 112 | (98) | 91 | (253) | 246 |
| E0100 | (8579) | 7779 | (117) | 123 | (105) | 99 | (237) | 249 |
| E0110 | (10001) | 7978 | (111) | 125 | (99) | 105 | (237) | 245 |
| E1000 | (5923) | 9098 | (126) | 118 | (137) | 197 | (214) | 146 |
| E1010 | (6113) | 4017 | (116) | 105 | (133) | 145 | (208) | 185 |
| E1100 | (5927) | 5097 | (?) | 128 | (?) | 231 | (?) | 122 |
| E1101 | (?) | 7980 | (156) | 132 | (202) | 206 | (179) | 151 |
| E1110 | (5193) | 3624 | (130) | 129 | (100) | 231 | (255) | 123 |
| E1111 | (?) | 5803 | (?) | 114 | (?) | 127 | (?) | 212 |
| E1200 | (4446) | 4746 | (137) | 170 | (230) | 199 | (132) | 196 |
| E1210 | (5955) | 4498 | (129) | 124 | (143) | 200 | (211) | 149 |
| E1001 | (9728) | 8721 | (124) | 122 | (141) | 110 | (208) | 237 |
| E1011 | (6394) | 5704 | (120) | 119 | (102) | 88 | (243) | 256 |
| E1201 | (6736) | 7932 | (122) | 123 | (130) | 120 | (217) | 228 |
| E1211 | (5159) | 5422 | (125) | 117 | (124) | 133 | (226) | 209 |
| E2000 | (?) | 4969 | (?) | 110 | (?) | 242 | (?) | 93 |
| E2010 | (?) | 4487 | (?) | 150 | (?) | 288 | (?) | 87 |
| E2011 | (?) | 5545 | (?) | 121 | (?) | 160 | (?) | 186 |
| E2001 | (?) | 7009 | (?) | 142 | (?) | 169 | (?) | 198 |
| E2100 | (?) | 4191 | (?) | 133 | (?) | 253 | (?) | 105 |
| E2200 | (4136) | 4143 | (154) | 158 | (277) | 280 | (102) | 103 |
| E2110 | (?) | 4532 | (?) | 154 | (?) | 266 | (?) | 113 |
| E2210 | (3601) | 4953 | (192) | 188 | (303) | 264 | (124) | 149 |
| E2101 | (?) | 6092 | (?) | 123 | (?) | 155 | (?) | 193 |
| E2201 | (5636) | 6689 | (138) | 145 | (191) | 187 | (172) | 183 |
| E2111 | (?) | 5691 | (?) | 114 | (?) | 191 | (?) | 148 |
| E2211 | (6220) | 5518 | (137) | 157 | (223) | 214 | (139) | 168 |
-
Initial number of firms, always = 225.
-
Note: Numbers within brackets are the results from same experiments conducted in Taymaz (1999). The two sets of experiments are identical except for the initial state year which has been moved up a couple of years in this paper, to allow statistical errors in the initial state (because of taxonomic differences between Planning Survey data and National Accounts data in the new C& C industry (Eliasson and Johansson, 1999 to sort themselves out in the markets of the MOSES model economy. For how to interpret these statistical error problems, see Albrecht (1992), and the text below. Apparently, they affect the relative outcomes of the experiments.
The E0000 experiment corresponds best to the calibrated case and industrial banking system type of finance. Interest rate arbitrage is slow, there is no stock market finance, and the interest rate is the same for all firms. Competition is modest. and a record number of firms remain on the horizon. Long term growth is fast but not exceptional.
Add individual interests (E0100) to this base run E0000 and investment allocations improve slightly. Make interest arbitrage faster (E0110) and long term growth improves further. The number of firms on the horizon has increased.
7.2.2. Experiments II: (Capital market regime)
Standard investment plans are based on expected long term profits. A firm’s period to period rate of borrowing over and above internal cash flows depends on the difference between expected rates of return and the individual borrowing rate. That limits investment for the period (except that ex post cash flows may not coincide with ex ante expectations). When stock market finance is allowed stock issues fill in up to the long-term plan (For details see Taymaz, 1999).
Add stock market finance to the base run (E0000), and a pure capital market regime with a standard interest rate to all firms (E1001) emerges that takes long term growth up to maximum level, through more entrants and fewer exits, as in E0110.
Keep the stock market evaluation but substitute tighter bank finance (individual and faster interest rates) for access to stock market financing of investments (E1110) and long-term growth drops radically. It helps a little bit if the individual interest rate is made dependent on a market valued debt equity ratio (E1210), apparently because the early selection of firms becomes more efficient and more and better firms survive. In both cases a high rate of firm exits has contributed to the reduced growth performance.
7.2.3. Experiments III (Securitized market)
Apparently, under the steady and predictable external (global) market circumstances of the experiments conducted so far maximum long term GNP growth performance is achieved under an industrial banking regime (E0100, or E0110), or a pure capital market regime (E1001) with only stock market financing and little involvement of banks. Mix the two (E1101) and long-term growth deteriorates somewhat, or a lot (E1111). A diminished firm population appears to be the reason for the deteriorated long run macroeconomic growth performance in that the increased exit rate is not covered up by new entrants. NewAdd options to the superior capital market performer (E2001) or the superior industrial banking performers (E2100, E2110) and long term performance deteriorates.
Apparently long-term economy wide performance is quite sensitive to choice of market regimes. The surprising outcome, however, is that adding market boosters to the successful industrial banking and capital market regimes in the form of options instruments turn out negative macroeconomic results, and predominanrly by raising the exit rate without a corresponding increase in the number of entrants (Cf E0100 with E2100 , and E0110 with E2110). Unfortunately, the available computer capacity did not allow us to trace down the exact reasons for that result. Previous experience from the model, however, tells that long term growth is positively associated with competition induced reorganization and reallocations of resources, but that the same structural change, if "too fast" also lowers price predictability in product markets. If market reallocations are too fast the consequent structural change makes current prices lose their predictive information about next period prices to the extent that misallocations of resources occur that instead lower long-term growth. Such negative long term consequences of overexcited markets should be expected to cumulate the closer to market clearing or balanced operating conditions the model economy is operating (Eliasson, 1983; Eliasson, 1984; Eliasson, 1991a; Eliasson and Taymaz, 2000; Eliasson et al., 2001). Since external (export) market conditions of the experimental design, as mentioned, are those of a global economy in approximate "stochastic market clearing equilibrium" also internal model markets will be sensitive to market speeds. Introducing derivatives in the model raises the speed of financial market arbitrage and perhaps too much when the economy is operating with very little slack and little room for positive short term resource reallocations. Increased market speeds will then cause market disorder at a time when the potential for large resource reallocation gains is small and cause an excessive exiting of firms. Experiments with options seem to illustrate this. Options experiments generally rank low and wind up on the horizon with exceptionally small firm poulations (E2100, E2200, E2110, E2210). When stock market financing is allowed, improvements can be observed, notably with firm specific but slow rate of interest arbitrage, and more firms survive (E2001, E2101, E 2201). Market volatility was at maximum under the securitized market regimes. Firms making losses on stock speculations had to pay high interest rates and/or go bankrupt, even though they might have been superb performers as producers. The exit rate in the options experiments is unusually high and the number of remaining firms on the horizon unusually low compared to all other experiments.
One of the three maximum performing experiments (E1001) features stock market financing in combination with general but slow interest rates. This capital market regime experiment exhibits less volatility and positive allocation outcomes that dominate over the negative influence of erratic price signaling in fast markets. Entry and exit rates are high but balanced and the number of firms on the horizon increases, rather than decreases.
The general result however is that change of market regime matters a lot for the long run macro outcome. This raises two questions about the relative importance of (1) external circumstances, and (2) initial conditions. Stable relative prices in global markets mean more predictable prices for exporters as well as domestic prices compared to the price pivoting experiments conducted in Eliasson (1983). The latter forced large structural adjustment in manufacturing industry, a transition that probably would have been more smoothly engineered by the sophisticated financial markets introduced in this study. Under long term predictable external market circumstances, on the other hand, firm management does not need to engage in high risk ventures into new technologies, and the simple profit plow back industrial banking financial regimes perform well, and also allow the entire economy to tick along at rates of "full employment and little unused capacities". Then speedier financial market regimes add little to macro economic performance, and may even destabilize market allocations of resources.
7.3. Comparative dynamics vs comparative statics
The second question on initial conditions is more intriguing. It is simply neglected by assumption in comparative statics modelling that dominates the field.
Standard practice in static equilibrium modelling is to compare two equilibrium states (comparative statics), before and after a regime change, and ignoring the structural adjustments involved in moving the economy between the two. Since no such determinate equilibrium state exists in the Moses model economy comparative statics does not make sense. Neither does the Moses economy operate on a neoclassical steady state equilibrium growth path. Comparing such steady states is sometimes called comparative dynamics, even though there is no market dynamics involved in determining their diverging paths. MOSES is selection based, highly non linear and initial state dependent. So, attention has to be paid to what its initial state means for its long term evolution. Only then can we talk about "true comparative dynamics". Even though the initial states are the same in all experiments for this study the paths the model economy takes into the future apparently are very different depending on which market regime we enact. And, by accident and discovered late, even small changes in initial conditions between these experiments and the same market experiments conducted in Taymaz (1999) tend to cumulate, as a comparison of the numbers within, and not within brackets show in Table 3. This complicates the evaluation of different market regimes for long term economic evolution considerably. Since this is a study in microsimulation method, and not an attempt to empirically evaluate the merits of different market regimes in a Sweden like industrial economy, we leave this observation as an experience for a future study, and then hopefully with more available computer capacity.
Paradoxically, however, the more primitive the financial system, and the faster the interest rate adjustment the faster the economy grows (Cf E0110 > E0100 > E0000). When a stock market (with stock market financing)30 is combined with passive commercial banking into a capital market regime (E1001) long term growth shoots up to maximum levels , but when a market for derivatives is introduced on top (E2001) entrepreneurial entry increases, but exits even more. With a smaller firm population on the horizon, and apparently a longer trail of economic mistakes Type II, long term growth suffers. Individualize firm interest rates (E2101) and long term growth recovers, and even more so when interest rates are made dependent on market valued debt equity ratios (E2201), because of a more efficient market sorting of firms.
Speeding up market adjustments of interest rates, however, does not stimulate long term GNP growth (cf E1001 > E1011 and E2001 > E2011). Too fast and too deep adjustments destabilize markets. When a derivatives market (with or without fast interest rate arbitrage) is added to a stock market regime with stock market financing and firm specific interest rates dependent on market valued debt/equity ratios, and hence very keen project selection, firm turnover increases. Apparently keener selection among more firms and derivatives do not combine well in supporting long term growth (Cf E1201 > E2201, E1211 ≈ E2211). In the fast interest adjustment case a more intense competitive elimination of firms apparently leaves on average equally productive firms, but fewer and larger. With more concentration fewer firms generates roughly the same long term growth outcome.
7.4. Financial speculation puts even profitable manufacturing firms at risk
Individual interest determination sometimes reduces long term growth, and the more so the more sophisticated the financial system. except, however, when individual interest rates are based on replacement valued debt/equity ratios. The reason for this odd result is that manufacturing firms have then lost money on portfolio speculation, suffered lost borrowing capacity and been forced to pay higher interest rates. These firms have then invested less and become more at risk of exiting. In principle such negative occurrences could also be the outcome of mistaken strategic acquisitions, of which there are plenty of real examples (Eliasson and Eliasson, 2000). Apparently, this negative consequence of strategic mistakes occurs more frequently in sophisticated financial systems that offer better opportunities for financial mismanagement, and has been sufficiently strong in our simulation experiments to affect long term economy wide outcomes. Allowing manufacturing firms to speculate in financial markets, which they are not good at, will therefore introduce noise in the market resource allocation machinery with adverse effect on long term growth.31 This effect is perfectly possible to understand from such experiments as an empirical phenomenon. To judge whether it is a serious social (economy wide) problem, however, requires more serious estimation work on the MOSES model, and careful sensitivity testing for the role of initial conditions.
While general interest rate determination combined with stock market financing increases long term growth (E1001 > E1011 > E1010), a fast interest rate arbitrage reduces that positive effect, as does a firm specific interest. Changes into a firm specific market valued debt equity ratio, on the other hand, does not change that outcome much,32 and if specifications are changed to individual interest determination with replacement valued equity and slow interest rate arbitrage there is no change in long term GNP growth. A negative outcome is however recorded if the interest rate adjustment is speeded up (E1001 >E1011).
7.4.1. Financial derivatives speed up markets
Financial derivatives boost the leverage of normal market mechanisms. If we now introduce options and derivatives the exit rate increases, and speculative portfolios are hit faster.33 The strongest effects occur if the interest rate depends on the firms’ stock market valuation. Capital losses on financial assets then hit the debt equity ratios on which individual firm interests depend. The firm’s borrowing rate shoots up. The introduction of financial options speed up changes in the market value of firms. An increased rate of exits occurs for the "wrong reasons", and a decreased number of firms and a diminished diversity of the firm population follow. Speeding up market arbitrage further in an economy that is already operating "statically efficiently" with a minimum of slack, which seems to be the case, makes market pricing more volatile, less predictable and more prone to business mistakes, which lowers long term growth. (This is so except when options are introduced in a stock market regime with individual, but slowly intermediated interest rates dependent on market valued debt equity ratios (E2211 > E1211), but the improvement is small). While macroeconomic performance improves almost universally when profitable firms can finance their investments in the stock market, the tentative summary reading of our simulation experiments is that with securitized financing (introducing call options) under our experimental design long term growth outcomes worsen. This result is accompanied by an increase in firm turnover, some of the new bankruptcies being caused by speculative financial portfolio losses by otherwise healthy manufacturing firms, being occasioned by the faster financial intermediation of the options. Economic fundamentals are destabilized and the incidence of what we call Type II economic mistakes increases.
7.4.2. Losing long term winners (Type II economic mistakes)
If we combine stock market finance with a general (slow) interest rate determination a very large improvement in long term output can be recorded (Cf E1001 >E0000), even though the exit rate increases significantly. This shift into a capital market regime has apparently led to an improved allocation of resources and a concentration to fewer high performance firms than in the reference base case. It should be noted, however, that for this to occur the market has to identify the long term winners very early in the simulation, and avoid forcing them to exit prematurely because of some unfortunate occurrence along the way.34 A faster interest rate adjustment (everything else the same, E1011) apparently eliminates that initial advantage, and the model economy is no longer capable of recovering that "loss", despite the more efficient resource allocations normally associated with a faster interest rate regime. Introducing options (E2011) or firm specific interest rate determination (E1111, E1211) or both (E2111, E2211) does not change the long term outcome much. Apparently, the slow financial market regime in the beginning of the experiments has saved some long term winners from being prematurely forced to exit because of accidental circumstances that became critical in the faster financial markets.
Maximum long-term output is achieved under (1) an industrial bank regime (E0110) and (2) a capital market regime with slow interest rate arbitrage (E1001). These are exactly contrary cases. In (2) resource allocation is entirely stock market intermediated, and in (1) filtered by the bank and the interest rate. Mixing the two regimes (as in E1111) confuses markets and long-term performance drops significantly. These results are interesting. Apparently, the selection of agents and/or the allocation of resources to firms at an early phase of the simulation can have a decisive impact on the long term by giving, or not giving, some long term winners an initial growth advantage. They lose that advantage in a fast capital market regime, and apparently also in an even faster securitized regime. We have not been able to figure out exactly how, but indicationas are that long term winners have been deprived of financing when the two high performance regimes were integrated.. This possibility was also observed theoretically in the competence bloc analysis of Eliasson and Eliasson (1996). It seems not to be possible to identify those future winners through improved market price signaling, which presents the market analyst with a tricky problem since the future high performance of these winners can partly be traced back to initial conditions, not however the circumstances that helped them along during the historic simulation. There is also the possibility that some of the long term winners lost, and especially in the securitized market regime, had engaged in loss making portfolio speculation and had had to exit because of that, despite a superb manufacturing performance. A different set of initial conditions (not those determined empirically in the Planning Survey of the Federation of Swedish Industries) might therefore have generated a very different long-term outcome. These were surprise results from explorative experiments on the MOSES model. For the time being we however lack the computing capacity to clarify the underlying "empirical" details of these results. However, the very documented fact that (by conventional definitions) efficient financial market regimes may not be sufficiently robust to prevent known winners to be depriverd of finance, and major Type II economic mistakes from being committed is interesting enough to warrant attention.
7.5. Turnover of firms
The entrepreneurial entry and exit characteristics of different financial regimes are particularly interesting. The peak performing regimes (E1000, E0110 and E1001) are characterized by a balanced and not particularly fast firm turnover. The long run low performing experiments exhibit a (much) higher exit than entry rate, caused by a faster interest arbitrage that in turn raises the rate of premature exits of Type II (see Sect. 2.3). Market selection thus matters for long term economy wide performance.
But the experimental picture is not uniform. Introducing options in a stock market with fast adjusting individually determined interest rates dependent on market valued debt equity ratios, long term growth did not change much. The increase in firm entrants and exits was, however, significant (E2211> E1211). When slowing the adjustment speed and removing stock market financing (ceteris paribus) long-term performance dropped sharply (E2211 > E2200) to the tune of an even larger increase in firm turnover. When interest arbitrage was instead speeded up (ceteris paribus), the rate of firm turnover shot up even more, and long term growth increased but much less so (E2210 > E2200).
A stock market regime combined with a slow interest arbitrage raises the exit rate, because of:
Volatile stock market valuations and/or
Losses in financial portfolios of manufacturing production firms
A generally competent and well managed manufacturing operation may thus crash because of unsuccessful financial portfolio management. This effect is leveraged up if the firm’s interest rate is made dependent on a market valued debt equity ratio.
The rates of entry and exit furthermore seem to be positively correlated suggesting that entrepreneurial entry raises (through increased competition) exits of incumbents and overoptimistic entrants. This correlation pattern has been documented in empirical studies (Geroski, 1995), but the model simulations add a plausible causal explanation to the same complementarity. Long term growth performance, however, is not necessarily positively correlated with the rate of turnover of firms (Cf E0110 and E1001), indicating that an efficient reallocation of resources over the credit market can occur without excessively killing low performing firms. We know however from parallel studies on MOSES (Eliasson and Taymaz, 2000; Eliasson et al., 2001) that fast entry must be accompanied by a corresponding fast exit of low performers and labor market mobility to keep factor price inflation from holding back growth in new expansive firms.
Summarizing so far, the industrial bank (E0110) and capital market (E1001) regimes individually improve the macro outcomes significantly compared to the base run (E0000) which is predominantly backed by interal finance. Mixing the two (in E1111) however lowers long term macro output. On the face of it entry is lowered somewhat compared to both, and exits are increased . The most probable reason is that markets have been speeded up further from the already efficient "static" allocation achieved separately in E1001 and E0110. Markets have been excessively excited, discouraging new entry and forcing more firms to exit, probably including long term winners that survived in the other two experiments. Changing from either into a securitized financial market system (E2002 and E2110) appears not to be a good idea. The negative long term growth outcomes of introducing options in an efficient industrial banking or capital market regime may be a surprise compared to the standard theoretical predictions of financial models. For one thing, however, we have only tried a primitive version of a securitized financial market. Secondly, however, and more to the point, external world market (export) prices by exogenous assumption have been almost in "stochastic equilibrium" in the sense that relative exogenous change in prices in the four subindustries are fluctuating around a slow inflation trend that under the adaptive expectations regime of the model firms will be quite predictable "in expectation". Hence also domestic markets will be predictable, meaning that an industrial market regime with firms being dominantly self-financed will work quite well, and a capital market regime with stock market financing should not, as demonstrated, be more than a marginal improvement. When, on the other hand, global markets are subjected to wrenching unpredictable change in prices, as in the price pivoting experiments on MOSES in Eliasson (1983), the improved flexibility in financial market resource reallocations associated (theoretically) with financial derivatives, should make for improvements in long term growth outcomes. In our experiments, on the other hand, with predictable global markets and a global economy operating close to market clearing with a minimum of slack, we have probably experienced again, what we have learned from many previous experiments, that an economy close to predictable market clearing, is sensitive to speedy market transactions, and that this may explain the negative outcomes of speeding up financial market transactions in our model experiments under such conditions. This is at least a reasonable hypothesis for future experiments on the Moses economy.
7.6. Experiments: R&D investments and strategic risks35
The strategic R&D investment module is one of the four modules where stochastic specifications enter (see Eliasson, 1985; Ballot and Taymaz, 1998). The firm faces a spectrum of R&D investment choices offering a tradeoff between a high probability of a normal return and a low probability of a very high return. This module was originally devised to allow individual firms to participate in a MOSES based business game, and to assign their own strategies, or for us (as outsiders) to characterize individual firms exogenously. In the simple version that we use here all firms adopt the same strategy, and outcomes become a chance drawing from the same distribution. For practical computer capacity reasons, we have had to limit the number of experiments to three:
No stock market – to be compared with E0000 or E0110
With stock market financing – to be compared with E1201 or E1001
Also with options – to be compared with E2201
The results (Table 4) are interesting. First, economy wide long-term outcomes are generally lower than in Table 3, but this is a technical result of scaling. The strategic module changes the average R&D pay off for all firms. Second, however, and important, going from an industrial bank regime dominated by internal financing and bank loans (E0000 and E0110) towards a capital market regime with stock market financing and a firm specific interest rate dependent on a market valued debt equity ratio the GNP outcome on the 60-year horizon more than doubles, as does the rate of exits of low performing firms. The reason for the strong performance is a substantial reallocation of resources to a smaller number of high-performance firms. The consequent higher concentration that reduces competition (a negative factor), has however been overshadowed by the market induced reallocation of resources and a flexible labor market to accommodate the change.
Stochastic R&D Choices
| Experiment | GNP | Enter | Exit | Number of firms on the horizon |
|---|---|---|---|---|
| E(0000) | 1842 | 143 | 93 | 275 |
| E(1201) | 4955 | 121 | 217 | 129 |
| E(2201) | 3297 | 135 | 169 | 191 |
-
Initial stock of firms, always = 225.
Shifting into a securitized financial market regime generates a much better long run outcome than that for the industrial banking regime but below that of the capital market regime. Contrary to the options results in Table 3 exits are lower this time. There are two explanations: (1) a worse selection of firms in the options case than in the capital market regime and/or (2) a consistently lower rate of return and less investments.
A more detailed comparison of the experiments showed that rates of return – as should be expected – were higher in the options experiment than in the stock market case. Still, the stock market experiment shows significantly larger investments, notably towards the end of the period when rates of return increase and an investment boom occurs. Apparently, this is the outcome of a series of circumstances we have observed before (e.g. in Eliasson and Lindberg, 1986) when firms in an early phase of the options experiment are forced to raise rate of return requirements because of the increase in interest rates (a result of the introduction of options). When finding fewer profitable investments, firms choose to lower their investment spending and reduce employment. (This does not necessarily have to be associated with an increase in exits forced by financial portfolio losses by manufacturing firms, as in earlier experiments). The opposite dynamic occurs in the stock market case. With softer rate of return requirements in the first part of the period firms slowly gear up for expansion that culminates with an investment boom during the second half of the of the 60-year simulation. With the higher exit rate of low performing firms in this case, the boom should be sustainable beyond the 60-year horizon. Again, however, a proper comparison of the outcomes of the different market regimes would require a series of complementary and longer run experiments than our current computer capacities allow. We therefore must give up on the ambition to explain the details of our results.
Complex circumstances surrounding the experiments, notably initial conditions, can tilt the outcome of one set of experiments (for instance the creation of a derivatives market) in very different ways. For the time being we cannot say that the "picture", emerging from the introduction of derivatives markets in the MOSES model (see above), namely that positive changes are small and mostly negative, carry any general implications, except that negative results from speeding up financial market arbitrage are likely to occur in an economy that is already structurally adjusted to competition in global markets. A structurally badly adjusted production system, on the other hand, should be forced through increased competition and turnover of firms to become globally competitive.
7.7. Experiments allowing insiders to inform the market
Modern insider legislation is a peculiar piece of legislation by which lack of information among some market players, for ethical reason has been the motivation for preventing informed market players to inform the market by profitable trading on their information, most likely at the social cost of reduced macro economic growth (Eliasson, 1990a; Antonov and Trofimov, 1992).
In the current calibrated version of the MOSES model insiders have no defined role. Dividends are proportional to profits by assumption (see Equation 1 and Equation 2 in section 4.3). Insiders hence know no more than outsiders. In the following experiments we introduce insiders with unique information and allow them to trade freely on their superior knowledge of, for instance successful outcomes of strategic R&D decisions (see previous section), and study the economy wide outcomes of how this new information affects the prices of shares, and indirectly makes the market more informed.36 Each firm has one insider (= the CEO operating as an investment firm) who can revise his private profit forecasts when he has made decisions on behalf of his firm, that will affect the market value of the firm, and buy or sell.
We should remember that "historically", for instance in Sweden, there were no restrictions preventing insiders from trading on their unique information. Today, market transparency and fairness requirements have made insider trading illegal. Several principal problems are however associated with insider legislation. First, there is the difficult distinction between trades based on particular information (a merger next Monday) and the unique understanding of a business associated with insidership. Second, while buying or selling on a piece of insider information is not allowed, abstaining from buying and selling privately on that same information has the same consequences, but cannot be legally enforced. Preventing insider trading thus not only deprives the market of information but also biases information flows (Eliasson, 1990a). It is therefore of interest to know what such artificial lack of information means for economy wide economic performance.
Beginning with the previous simulation experiments on strategic R&D investments we may observe that insiders involved in the decisions should in principle invest in the company conducting the R&D investment as owners and pilots telling the market that they believe in the strategy. For years, their continued investment in the firm will probably be based on their insider understanding and personal judgment of the consequences of the R&D venture. At some point, for instance advance information on the success of clinical tests of a medical substance, that understanding of the insider changes its legal character and becomes a piece of insider information and is outlawed.
We have no reason to expect that insiders in a firm have a better economy wide understanding than anybody else. We should however expect the insider on a strategic R&D project to have a better understanding of how the economy wide future will interact positively with the outcome of the R&D project, this being an important part of the business idea.
We have studied the role of insiders in an economy on the MOSES model. In terms of the MOSES firm a strategic R&D project will have a positive effect on the capital and labor productivities of the firm (INVEFF and MTEC respectively).37 The insiders upgrade the productivity characteristics of their firms by entering the new R&D based productivity data into the production modules of their firm,38 to be able to compute a new expected RN to be inserted in Equation 1 in Section 4.3. The insider then constantly buys shares in his company at a constant rate if the market price is lower than (say 80 percent of) what the insider has computed. Other agents (speculators and firms) in the model form "short run" and "long run" stock price expectations, P(SR) and P(LR). P(SR) is formed by regressing the stock price on lagged values (short run behavior), and P(LR) is based on the discounted value of expected dividend payments in the future. Expected dividend payments are calculated from the forecasts based on past dividends. The bid price of agents is a weighted average of P(SR) and P(LR) where the weights may differ between agents.
If an agent has insider information about a firm, it will use that information in determining its bid price. In our experiments we assume that insiders can get information about radical and incremental innovations of the firm. The insider then revises its "long run" stock price expectation as:
P̿(LR) = P(LR)· (1+y│∆T - ∆Tᴹ│)
where y is the adjustment parameter, ∆T the change in technical level of the firm in question, and ∆Tᴹ average technical change in the market (assumed to be observed as changes in productivity at industry level). The "expected "short run" stock price is not revised because agents assume that it is driven entirely by short run changes in stock prices. An upward revision of the expected "long run" stock price may of course increase the demand for the stocks of that firm, and that stock price may in turn increase the expected next period "short run" stock price.
We have run three sets of insider experiments. In the first set there are no insiders. In the second agents have a 1 percent probability to obtain insider information about any given firm. We assume that the positions of agents are determined at the beginning of the simulation, and do not change over time. In the third set the probability of being an insider is 10 percent.
All experiments are run for 60 years by quarter. Results are summarized in Table 5. They are quite interesting. In general, but not always, the presence of insiders increases long term economic growth by making the market more informed, and the allocation of resources more efficient. With stock market financing of investments, individual interest rates based on market evaluation of risks (debt equity ratios), and high speed interest arbitrage (E1211) insider information appears most potent in improving long run outcomes. Apparently, insiders do the positive information and growth jobs we expected the derivatives market to do.
Insider Experiments
| Exp | No insider | Insider rob. 1% | Insider prob. 10% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GNP | Entry | Exit | GNP | Entry | Exit | GNP | Entry | Exit | |
| E1201 | 3688 | 583 | 178 | 4429 | 412 | 181 | 4287 | 423 | 180 |
| E1200 | 2828 | 485 | 226 | 2754 | 587 | 245 | 3499 | 581 | 241 |
| E1211 | 3609 | 424 | 170 | 3161 | 482 | 191 | 4899 | 483 | 194 |
| E2201 | 2789 | 496 | 238 | 3546 | 500 | 285 | 3086 | 528 | 255 |
| E1101 | 4704 | 398 | 140 | 4734 | 611 | 117 | 3973 | 373 | 136 |
| E1001 | 4374 | 414 | 99 | 4430 | 480 | 122 | 4597 | 466 | 91 |
8. Implications for policy
Change of financial market regime has been found to cause large differences in economy wide long term outcomes. Given a predictable long term global market price scenario, an internal finance based industrial bank system or a capital market regime based on stock market finance, appears to be best for promoting long term growth. Mix the two, or worse, introduce an options (securitized) system on top of either one, and growth outcomes deteriorate significantly. The reason is that speeded up financial markets disturbs, rather than improves allocative performance in an economy which has already achieved an allocation of physical resources that is internationally competitive. There was little additional scope for neither short term slack reduction nor faster reallocations of workers over the labour market. Under a predictable long term global product market scenario, and firms governed by adaptive price expectations more broad based and faster financial market arbitrage thus added little to economy wide long term growth performance. Profit plow back supported by bank finance of rapidly expanding firms offered as much financial market induced growth as was possible under a given technological regime. These are "theoretical" simulation results on a calibrated model. Even though limited computer capacity has prevented us from testing for the robustness of these results by Monte Carlo experiments, we feel comfortable concluding that they illustrate the difficulties for politicians of designing an optimal financial market regime under the complex realistic circumstances of our analysis. We refer to the results from simulation experiments on the agent based model MOSES, calibrated to represent a "Sweden like industrial economy, as theoretical, but with sufficient empirical relevance to be taken seriously.
By implication we also venture as a proposition to test in further experiments, when sufficient computer capacity has become available, what happens under a more volatile and long term unpredictable global product market scenario. Presumably, a securitized financial market regime would then more efficiently force failing firms to exit faster, and free resources for faster long term economy wide growth. If the theoretical and empirical results from static general equilibrium modeling , for instance those by Allen and Gale (1994), have any relevance for a real economy, this is what they must have had in mind. But even so, the results so far from MOSES simulations present policy makers with a formidable problem. High speed financial market arbitrage doesn’t seem to be generally good for the economy. (The experiments of this study show the Moses model to be very sensitive to choice of financial market regime, and to respond strongly negatively over the long term to increased financial market speeds when the economy is already structurally well adjusted to product and factor market prices. To redesign financial market regimes according to unreliable forecasts of long term product market and technology change therefore require far more sophisticated policy designs than seem to have been understood in literature).
8.1. The magnitudes involved
To make a point of the magnitudes involved thus moves the analysis into difficult empirical terrain. Then the empirical relevance of calibrated parameters, notably those related to dynamic Stockholm School market feed backs, becomes important, and we are not yet ready to formulate strong conclusions on that. Even so, let us go through the quantitative differences between the many experiments, and discuss to what extent the absolute magnitudes and the differences between the experiments carry empirical information on a Sweden like industrial economy.
The difference between the minimum (E1110, E2100, E2200) and maximum performing market regimes (E0110, E1000,E1001) is about 1 to 2.5 corresponding to an annual difference in GNP growth over the entire 60 year period of about 1.5 percentage points, and these differences have been caused by only switching between two pairs if financial market parameters. But even seemingly minor such changes can cause dramatic drops in long term economy wide performance (E2211 >E2210 or E1111 > E1110). We have already warned about the importance of controlling for biases caused by stochastic events through Monte Carlo sensitivity tests. The very possibility furthermore of seemingly insignificant circumstances cumulating into major economy wide change with time, typical of nonlinear initial state dependent and selection-based models, are characteristics likely to also characterize real economies, and should be taken seriously when showing up in model simulations. Speeded up markets in an already efficient model economy are likely to prematurely kill more winners or to generate more Type II economic mistakes the consequences of which then cumulate over the sixty year simulation. It is our belief that such consequences explain the seriously worsened economy wide outcome when introducing securitized financial instruments. It is again possible in principle to check back through frequent reruns of the model to what extent this is the reason. This would however be a major new study that would require computing capacity that we currently don’t have.
To what extent the higher complexity of the real economy compared to the MOSES model adds robustness and makes it less sensitive to small perturbances is a different and interesting, but difficult possibility that we leave for later studies.
8.2. The economy wide effects of emerging markets for financial derivatives
The original problem of this essay was whether the new C&C technologies and the new financial products made possible by these new technologies, will improve the allocation of resources to the benefit of long-term economy wide development, and to what extent they will have a stabilizing or destabilizing influence on markets and economic systems behavior. Simulation analyses on the Swedish Moses model have given numerically precise answers to those questions. The corollary question however is how empirically credible they are. A first such question is to what extent these new financial products have helped to pull resources out of badly managed firms and reallocated them over markets to more promising firms. Will the result be more efficient investments and faster long-term growth in the Sweden like Moses model economy? One result seems clear. If the economy is already operating on an efficiently allocated structure of resources the scope for fast reallocational gains is limited and if pushed for too ambitiously, by for instance policy, is likely to destabilize markets and reduce liong run economy wide outcomes.
A second question is to what extent the global product market assumptions have limited the generality of these results. On this we have opted for a partial experimental design with a predictable global product market scenario for firms with adaptive price expectations. Such an experimental design, we realized late, would benefit an economy populated with profitable globally competitive firms, so shaped by having been subjected to global competition for a long time, as was the case with Swedish manufacturing industry, and hence the Sweden like model economy Moses. Under such circumstances profit plow back into existing firms complemented by (industrial) bank finance should generate satisfactory long term growth, as has also been borne out by the experiments. Under those assumptions speeded up financial market arbitrage would not necessarily benefit growth. As the experiments indicate it might rather disturb markets, lower price predictability under adaptive expectations. Resource allocations will be less informed and worsen long run growth outcomes, an interpretation that is supported by previous model experiments, for instance in Eliasson (1983); Eliasson (1984) and Eliasson (1991a). This adds a third concern for the policy maker, namely to what extent the model economy has been sufficiently diverse and robust to benefit from faster and more efficient financial arbitrage. Deficient diversity of structures is likely to be a deficiency of all micro based model abstractions of a real economy. The quantitative importance of this deficiency can however in principle be tested for by adding more firms to the Moses model and making entrepreneurial entry more vigorous which the early experiments in Eliasson (1991b) also support.
We began with a crude industrial banking financial market regime (only one bank), with internal financing being the dominant form of firm finance. Such a system, lacking open financial markets for across firm resource transfer makes it possible for Government to control to some extent, through bank regulation, the allocation of financial resources in the economy. Such was the financial market regime in Sweden during the early post WWII period through much of the 1980s. The Swedish Government used credit market controls to provide cheap financing for public sector growth, and to patronize a select group of large export firms. This worked OK (1) until the market destabilizing influence of counteracting savers that were earning large negative real interests after inflation and taxes, and increasing financial across border leakage forced a policy reversal (Eliasson and Taymaz, 1992) and (2), until global technological change subjected Swedish export producers to new and radical demands for structural adjustments during the 1990s. New C&C technology based financial products and the introduction of a capital market financial regime helped a new and more flexible financial market scenario materialize. We therefore introduced first a capital market regime in MOSES of the type gradually introduced in Sweden from the second half of the 1980s, and then some rudiments of a securitized financial system. Again, such a securitized financial regime became an increasing reality in Sweden in the first decade of the new millennium. The three levels of financial market sophistication and regimentation in fact correspond to the situation in Europe in the 1960s (industrial banking backed up by exchange controls), in the 1970s and part of the 1980s (a gradual break up of exchange controls caused by international market arbitrage, "euro dollars"), and from the late 1980s an increasing securitization of the financial systems. While the experiments in this study have been designed to represent political and institutional development, unfortunately the external global market was assumed to be the same, which reduced the generality of the experimental designs.
Simulation results tell the following:
Introducing stock market financing associated with a capital market regime generally improves profitability filtering of investment projects (E1001) and hence the long run allocation of resources and economic growth.
The surprise result, however, is that an industrial banking regime with very limited resources being reallocated between firms through the bank functions equally well (E0110) and that mixing the two regimes (E1111) does not seem to work at all. One reason for the industrial bank regime, with investments predominantly based on internal firm saving feed backs and bank loans, to function well probably39 is that the external market conditions were stable and predictable and did not require fast reallocations of resources between firms. Faster and more efficient financial market arbitrage did rather disturb markets and destabilize the economy.
Introducing a primitive market for derivatives gave no clear results. In some scenarios (for instance E2211 > E2210) improvements in the allocation of funds over the stock market raised firm turnover and long-term growth somewhat. In general, however, the introduction of a market for options appeared to disturb a delicate financial allocation machinery with long term negative consequences.
The long term consequences of raising the level of financial market sophistication appeared to be sensitive to particular circumstances, notably initial conditions, for instance an initially inefficient production structure.
So much said, policy interventions in a fast securitized regime can tilt the long term growth outcome in very unpredictable directions.
One hypothesis emerging from the experiments therefore is that the change into a capital market regime in the volatile global product market conditions from the late 1970s would have contributed to long term economic growth through making transfers of funds between firms over the market possible. Introducing an options market however appeared to cause few such positive effects, and rather the opposite in that a sensitive financial allocation machinery was disturbed.
The implications for policy for the securitization of financial markets may be far reaching. Policy authorities appear to lose control rather than being able to benefit from the faster market arbitrage. Since new C&C technologies allow securitization to occur whether policy makers like it or not, there appears not to be much choice. True, options are only part of a fully securitized market of the kind already introduced in the US, but since they alone seem capable of generating undesirable unpredictable outcomes one would expect a fully securitized system to have an even stronger long term economy wide impact. Again, however, the diversity of structures and robustness of the Moses model compared to the real economy it is supposed to represent, warrants caution of interpretation. The real Swedish economy should be more robust. The extent to which that difference matters can be tested in two ways; (1) by rerunning the experiments in a more volatile global market environment that would require flexible responses of both firms and financial markets, and (2), given (1), increasing the population of firms initially and through entrepreneurial entry.
In general, however, the economies "worst positioned" for a securitized financial system are those of the industrially underdeveloped world with raw material based economies, primitive markets and often corrupt politicians. When they complain (as Mahathir of Malaysia has done frequently40) they have a reason, because their economies are so undiversified, and their producers so protected from external competition that even minor changes in status quo may cause severe disruption.
Also, European economies may be in for trouble as C&C based securitized financial markets gain terrain. Many countries overprotect their producers, and are weighed down by very large and inflexible non-market public sectors protected from external market competition and dependent on easy and cheap external finance. With large inflexible, often politicized non market systems, structural adjustments caused by market competition are "transferred" by markets to the flexible private sector causing instabilities, if too fast.41
The US economy is the opposite example. Stable and fast long term growth appears to be supported by innovative entrepreneurial entry, and the success of the US economy through the 1990s up to the present appears to rest not only on its entrepreneurial culture and people but also entrepreneurs that have been supported by a uniquely innovative financial system, and fairly complete competence blocs with industrially competent venture capitalists (Eliasson, 1997). Not to be missed is that US politicians have allowed foreign competition to wipe out low productivity manufacturing businesses to an extent not seen in other parts of the world. Workers have been forced to move on to higher productivity jobs. Under such demanding market circumstances and strong flows of disruptive mew technologies, securitization of financial markets should generally have positive long term outcomes, an interpretation in keeping with Rybsczynski (1993).
8.3. Empirical credibility
Reasoning based on theory or model abstractions can be no more than tentative hypotheses to be subjected to further empirical testing. Hopefully, however, the hypotheses should be sufficiently empirical to mean something in a (political) decision context. We may have taken some liberties here in generalizing from the simulation experiments. On the other hand, the propositions made are quite in keeping with what we know, and perfectly testable on new data and (!!!) additional simulation experiments on the Moses model. The latter is a great advantage of complex micro simulation modelling. Very much as you try to explain observed empirical phenomena by collecting more statistics, you can ask the Moses model for more information about what it has told you.
The empirical credibility of Moses has been a concern in many studies. It rests on four pillars; (1) a well-researched and relevant prior specification, which sets it apart from most economic models (Eliasson, 1976a; Eliasson, 1976b), (2) an economy wide specification that integrates at least four well known partial models, two of which (Keynesian macro demand, and Schumpeterian innovation push) have been widely used individually for policy prescription, (3) the collection of a customized firm database, that besides being a high quality micro to macro and stock flow consistent description of the initial state, and integrated with the Swedish national accounts (Albrecht et al., 1992), also allowed us to (4) substitute direct measurement in many places for parameter estimation. The latter is important in a microsimulation context.
Complex model specification made possible by the micro simulation method has the great advantage of moving model design closer to direct observation and measurement, in many places doing away with the need for parameter estimation and stochastic assumptions. Thus, for instance, exit of an agent has been directly modelled on bankruptcy law. Firms exit individually when their equity has lost too much in value, and at the latest when it has been reduced to zero, and whatever asset values remaining at exit are returned to owners and the market. There is then no need to estimate artificial "probability of exit functions". Workers are laid off according to Swedish labor market law, and leave unemployment when wage offers exceed their unemployment benefits by a margin (this reservation wage threshold has been taken directly from Swedish labor market studies. See Eliasson, 1977). The Planning Survey of the Federation of Swedish Industries has made it possible to "measure" the initial state production structures of firms directly, such that they can then be upgraded by engineering calculations from period to period (Eliasson, 1976b).
All this means that the number of parameters to be estimated has been reduced to about a dozen critical factors that figure importantly as market determining time reaction and firm behavioral parameters. They are the parameters that regulate intertemporal behavior of the entire model economy from period to period, notably those that regulate Stockholm School ex ante ex post dynamics. Most of them are operational in that they correspond to "control levers" firm managers recognize. Even though we currently calibrate the model assuming these time reaction parameters to be the same for all firms, it is perfectly possible, using the panel data of the annual Planning Survey to "estimate" them individually, or better, to call in real firm managers for a gigantic simulation game to set their own firm parameters (Eliasson, 1985). Above all, however, whether estimated or calibrated the parameters will be surrounded by sizable confidence intervals. In empirical studies we therefore conduct Monte Carlo studies to see how sensitive our results are to small variations in parameter estimates. Unfortunately for this study computer capacity has not been sufficient for much in the form of such systematic evaluations.
Still, considering all empirical inputs in the MOSES model we regard it as an empirically credible representation of a Sweden like industrial economy. This means that we, being responsible for its design and construction, including its prior assumptions, take even surprise outcomes of model simulations seriously as something to be concerned about. They may occur.
Footnotes
1.
An early version of that innovation module is found in Carlsson et al. (1997). We plan tentatively to introduce a venture capital application in that module that endogenizes the selection of winning projects from R&D investments by modelling the industrial competence of venture capitalists as they learn from investment experience. Below we discuss the role of insiders in MOSES as they inform the market through, and learn from their trades.
2.
Technical details are presented in Taymaz (1999).
3.
Note already here that this selection becomes theoretically irrelevant if we reduce the state space by assumption to the narrow fully transparent one of the WAD model. Market selection draws transactions costs and innovative behavior therefore cannot occur in the WAD model.
4.
For practical data availability reasons the statistical resolution of the MOSES model defines the firm or the division of a firm as the minimum, autonomous market agent. Carleson (1991) has however taken measurement down to a finer level of resolution within the so defined MOSES agent, and demonstrated quantitatively how the large part of aggregate productivity change has been intermediated by reorganizing production structures.
5.
There is a fine distinction here. Industrial policy in the sense of targeting successful macro outcomes by way of interfering with the Schumpeterian Creative Destruction process of Table 1 is theoretically impossible and bound to fail (Eliasson, 2000b). It requires a one-shot successful policy outcome, which we have failed repeatedly to achieve by designed policy experiments on the MOSES model. Some long term improvement can be achieved after a series of policy experiments. To the extent the MOSES model is regarded as a realistic representation of the real economy such experiments can then be regarded as a learning experience for real policy.
6.
This may be because few of these models¸ if any, are really agent based, featuring both heterogenous agents and Stockholm School expectations plan outcome feed backs, as well as agent selection and economy wide market self-organization, which together give the MOSES model unique and empirically recognizable properties. See further below.
7.
Note that our concept of a business or investment opportunities space has little to do with similar concepts appearing in neoclassical literature, which always imply a space with almost fully known opportunities. Our point is to assume the opportunities space to be sufficiently large and complex to make it mostly unknown to each and all actors. Since opportunities depend on how each actor reacts to the decisions of all heterogeneous and differently sized actors in the market there is no theoretical chance for even a reasonably informed market except by awkward assumption. We claim that ours is an empirically reasonable assumption. Smith and Watts (1992), on the other hand, define the opportunities set to be captured by the ratio of the market to the booked value of the firm. S &W hence assume that there exists a marginal group of actors in the market that is fully informed about the size and the economic value of all opportunities. This is a typical assumption of static equilibrium neoclassical economics that the MOSES model has long departed from.
8.
Since this is a theoretical paper, we want to be strict on this point. The state spaces of the EOE and of the MOSES model are not infinite. At each point in time the state space is sufficiently large, but still bounded from above, to keep all agents, including central government, ignorant of all that can be known about its content, except for a fraction that differs between agents. To prevent the unrealistic consequence that with time everything will eventually be learned about we impose an Information Paradox (Eliasson, 1990b; Eliasson, 2001) stating that the opportunities space expands from (costly) exploration of agents, and faster the more intense that exploration in that firms, being challenged, learn and discover new combinations (innovation). We furthermore make the empirical assumption that the opportunities space thereby expands faster than all exploring agents can learn about its expanding content. Therefore, we acknowledge the empirical possibility (the paradox) that the markets are getting increasingly ignorant of what can in principle be known. In MOSES analysis we frequently refer to this as the Särimner Proposition, from then pig in the Viking Sagas that was eaten for supper in Valhalla by the constantly brawling Vikings, but came back next morning, to be eaten again next evening (Eliasson, 1987; Eliasson, 1992a). We depart from the Viking analogy in that the opportunities space grows from being explored. The game is positive.
9.
To discount a future flow of profits requires a known future discounting rate, which is assumed in the WAD model. We rather think of it as an ex ante concept, and that trades take place in the corresponding expected present values, that therefore both differ between agents and frequently turn out mistaken ex post. This is where Stockholm School economics enter (Eliasson, 1993; Eliasson, 2000a).
10.
Original ambitions were much higher, but modelling more complex matching on trading floors placed impossible demands on available computing capacity. Since the markets we are studying are largely made up of computerized transactions this problem illustrates the importance of C&C technology for the existence of these markets and suggests that the random pairing device may be an empirically acceptable simplification to begin with.
11.
For Model Of the Swedish Economic System.
12.
In principle households also face convex utility sets, even though they are assumed to be atomic in size and all identical (“representartive”) satisfying the conditions for a Stone type aggregate consumption system with a Friedman (1957) type permanent income consumption target and a Modigliani and Brumberg (1955) life cycle saving proposition, all modified onto a non linear format with saving as a separate future consumption category. For more details, see Eliasson (1985).
13.
Through a separate survey to C&C firms, which made it possible to separate out that new sub industry from the investment goods sub industry and the private services sector in the input output table, a major statistical job, in fact.
14.
As noted in footnote 1.
15.
Firms may make strategic decisions on whether to opt boldly for high risk ventures with a low probability of a very high return, and vice versa for a high probability of an acceptable return or any strategy in between. In fact, it would even be possible to assign predictable such strategies to the real firms in the model, or the firms could be asked to characterize themselves before a simulation experiment (see Eliasson, 1985). For practical reasons this mechanism has been turned off in the experiments reported on in this paper.
16.
Excess profitability so defined is called ꜫ in (3a) in Eliasson (1991a).
17.
This R&D module of Ballot and Taymaz (1998), which has not been used in the experiments of this paper, endogenizes the best practice technologies associated with new investments previously being exogenous.
18.
For a methodological discussion of generalizing from micro to macro, using the MOSES model, see Eliasson (2000c).
19.
For that reason, we prefer to refer to sub industry aggregates as markets rather than sectors.
20.
Computable general equilibrium models, even though frequently used for such calculations, are not recommendable. They are static and as a rule sector models and hence lack the market dynamics that is our concern.
21.
The rest of this section draws directly on Eliasson (1988), Eliasson (1998c); Eliasson (2000b).
22.
This aspect is being addressed in a currently ongoing study , that has later been published as Ballot et al. (2006).
23.
For preliminary work on introducing insiders in the MOSES model, see Trofimov (1995).
24.
See Eliasson (1985) and proof on page 238.
25.
Data on ԑ = R – r is collected annually in the Planning Survey of the Federation of Swedish Industries that is the basic statistical source of micro data for the MOSES model. See for instance Albrecht et al. (1992).
26.
Defined as the expected or actual variance in the prices of securities.
27.
All markets experience a similar pattern of global price fluctuations in the experiments of this study, the only difference being the timing of fluctuations. The trends change relative market prices as in the past period for which this model version has been calibrated and are then exrapolated. The implications of such exogenous global scenarios that are exogenously entered are discussed in Eliasson (1983) where the global long term balanced relation between productivities of best practice technologies, product prices and the international interest rate are specified. Experiments have been run on a model version calibrated as described in Taymaz (1991b).
28.
Exogenous in earlier versions of the model but endogenized on a firm basis in the simulation experiments in this paper as introduced with the new firm innovation module of Carlsson et al. (1997) and Ballot and Taymaz (1998).
29.
The first 6 years are used to generate the data needed for the stock market
30.
Note (when comparing E1001 > E1000 > E1010) that with stock market valuation of shares, but stock market financing no longer allowed, long term growth is lowered. This negative effect is further reinforced if interest rate adjustments are speeded up. This unexpected growth performance is explained by an increased rate of firm exits that is not compensated by an increased rate of entry of firms with more productive new technologies.
31.
If a bad market evaluation of a firm’s shares does not influence its individual borrowing rate macro performance may improve. This means that the bank has not been well informed, and has taken on more risk. Cf E1100 > E1200 and E0110 > E2211, but E1001 > E0110
32.
E1001 > E1101, E1011 > E1111 and E1010 > E1110. Furthermore E1101 ≈ E1201, E1111≈ E1211 and E1110 ≈E1210
33.
Note that for the time being we only have call options in the model.
34.
These are called Type II economic mistakes in Eliasson and Eliasson (1996), who expect Type II mistakes to be quite frequent. Competence bloc theory has been developed to explain the efficiency of market selection of investment projects. The ambition is to introduce competence blocs in the Moses economy.
35.
Currently not part of the standard calibrated model.
36.
Eliasson, 1990a suggests that the information embodied in insider trading may be too economically valuable to be lost by outlawing insider trading. A better way would be to enforce the use of modern C&C technology to immediately let the market know about an insider trade. John and Mishra (1990) use a general equilibrium model to demonstrate how a new equilibrium can be reached with insiders informing the market (“signalling”) through trades.
37.
The markets of the MOSES model are assumed to perfectly trade product quality against product volume. Hence INVEFF and MTEC will reflect product quality improvements. For the outcomes of this insider experiment this is not important, but in other experiments it is. See discussion of product market arbitrage in Eliasson (1976b).
38.
i.e. the α and β in Equations 4 and 5 in Eliasson (1991a). The insider then computes the consequent increase in Rn in (3B), and finally inserts Rn in equation (1) in Section 4.3.
39.
We did not expect this result, and therefore did not prepare for a second round of experiments to check for reasons. Because of the extraordinary demands on computer capacity that were temporarily overcome, this has not yet been possible.
40.
Mahathir has recently also added e-business to his list of complaints (Financial Times, April 22. 2000:3).
41.
Economy wide instability caused by a large inflexible public sector in combination with speeded up market resource allocations has consistently shown up in Moses experiments (see for instance Eliasson, 1986a; Eliasson, 1986b; Eliasson and Taymaz, 1992).
42.
Paper prepared for the project at KTH: The Macroeconomic Effects of Computer and Communications Technology, funded by the Swedish Transport and Communications Research Board (Kommunikations- forskningsberedningen). Published as Stockholm: KTH TRITA-IEO-R 1999-09.
43.
44.
“Short run” refers to expectations for the next quarter.
45.
The number of models that can be used for forecasting in unlimited. In our experiments, we used only two simple forecasting models. See also Antonov and Trofimov (1993).
46.
In the model, we also introduce a small random variation (at most 10% of the expected price) for expectations to account for various types of information the agents may get.
47.
On a model version calibrated as described in Taymaz (1991a).
Appendix A
by Erol Taymaz
A.1. Modeling the stock and derivatives markets in MOSES42
A.1.1 Abstract
The stock market in the MOSES model is specified.43 It is modeled in a modular form where agents first form expectations about expected stock prices, buy and sell stocks in the stock market, and buy and sell options in the options market.
A.1.2 Agents
There are two types of agents in the stock market, firms and investors. MOSES firms can buy and sell stocks in the stock market, including their own firm’s stock. Because of the entry and exit processes, the number of firms in the market is endogenously determined. Investors are rich individuals, institutional investors and speculators that own stocks. There are 50 investors in the market and there is no entry process for investors. If the value of an investor’s portfolio goes to nil, the investor stops buying stock in the markets, i.e., he exits.
A.1.3 Expectations
Agents (investors and firms) form expectations about short run changes in stock prices,44 dividend payments, and the long run values of stocks. The short run stock price is estimated by using the following models.45
where P is the stock price, D dividend payments, and e the error term. The first model is a simple autoregressive model whereas in the second model, the lagged amount of dividend payments is also used to forecast the stock price.
The amount of dividend payments at time t is also forecasted by using first and second order autoregressive models:
The dividend flows may exhibit erratic changes and structural breaks. Therefore, the dividend models were tested for structural changes in a simple way. The model is first estimated for ne periods. The same model is then reestimated by dropping the two most recent observations. If the change in parameter values is greater than a certain predetermined level, agents assume that there is a structural change in the process that generates dividend flows. Therefore, they do not use the autoregressive models (Equations A3 and A4) but use the arithmetic average of the last na periods to determine their dividend forecasts.
Agents base their decisions on long run changes and calculate the stock price from the net present value of future dividend flows. They use either Equation A3 or Equation A4 to forecast future dividend flows, and calculate the net preset value (NPV) of dividend flows per stock:
where E(Dt) is the expected value of dividend payments at time t, i the discount factor (a simple weighted average of past interest rates), and nf the planning horizon. The expected values of dividend payments are found by using one of the following regression models.
In other words, agents first estimate Equations A6 and A7, then use the estimated parameter values to generate dividend forecasts.
The long run expected stock price is then equal to
where NW is the net worth of the firm, and nst the number of stocks. Hence, we assume that the long run expected price of the stock cannot be less than the net value of the firm per share, because an investor can get NW by dissolving the firm at time t.
Finally, agents calculate the risks of their estimations. The short run risk factor, RISK, depends on the agent’s risk aversion (an exogenous parameter), the stock’s BETA value, and the precision of price and dividend forecasts as measured by the R2 of the model used by the agent. The expected short run risk-adjusted price is calculated as follows:
where E(Ptsra) is the expected risk-adjusted “price” (including the return in dividends), Pt* and Dt* are the expected values of stock price and dividend payments, as forecasted by using Equations A1-4, and RISK the riskiness of the stock.
The expected long run risk-adjusted price is calculated as follows:
where Pt+ is the expected long run price (Equation A6), R2 the R2 of the (Equation A3 or Equation A4) used to forecast future dividend flows, and a a parameter.
The long run and short run price expectations are then combined:
where θ is a parameter that reflects agents speculative motives (0 ≤ θ ≤ 1). If the agent is a pure speculator, then he will rely on short term changes in the stock price only to make a profit, hence θ = 0.46
The demand for and supply of stocks in the market is determined by the offer price and price expectations. If the offer price in this quarter is less than the present value of the expected price in the next quarter, then the agent will be willing to buy the stock. Hence, the desired change in stocks is defined as follows:
where Soffer is the amount of stock offered in the market (if Soffer > 0, the agent wants to buy stocks, if Soffer < 0, then the agent wants to sell stocks), and Srespon is the responsiveness parameter. The greater the value of srespon, the greater and faster the reaction of the agent to price differentials in the stock market. Since agents may have different expectations about future prices (because they use different models for forecasts, they combine short run and long run expectations differently, they may have different attitudes towards risks, etc.), those who believe that the stock price will increase tend to buy stock this quarter, and others tend to sell stocks. The offer price, Poffer, is found through an iterative process that equates total supply to total demand for each stock.
A.1.4 Options and derivatives
The options market is modeled similarly. The main difference between the stock and options markets is the fact that option transactions are modeled to take place between a couple of agents. Therefore, agents are randomly matched with each other, and if their price expectations are sufficiently different, then the agent who believes the stock price will increase buys the option from the other agent where the strike price is determined within the range of buyer’s and seller’s expected prices. For simplicity, we assume that there are only call options, i.e., the holder has the right to buy the stock at the exercise date, which is one quarter after the agreement. The holder (buyer) pays the option price (defined as a certain percentage of the value of the option) to the seller when they sign the contract. At the exercise date, if the stock price is higher than the strike price, the holder buys the stocks from the seller at the strike price. Otherwise, the option will not be exercised.
A.1.5 Experiments
We have run a set of experiments to test the effects of introducing the stock market into the economy.47 Compared to earlier versions the MOSES model now has both stock and options markets, individual firm interest rates and interest rate adjustments, and allows access to the stock market for investment financing. Unfortunately, intermediation in the stock and derivatives markets are extremely demanding on computer capacity. As a consequence it a has not been possible to conduct Monte Carlo variations around each experiment (as in Eliasson, 1999a), varying the stochastic assumptions to test for robustness of results. This very fact, however, at the same time illustrates the importance for the development of dynamic markets for derivatives of computer and communications technology. These markets essentially consist of computerized trade in mathematical algorithms (Eliasson, 1999b).
Each experiment is defined as a
combination where the first x shows the existence of stock/options markets (x1 = 0, if there is no stock market, = 1 if the stock market exists, = 2 if the options market exists); the second x indicates the interest rate specification (x2 = 0 if the interest rate is same for all firms, = 1 if it is firm-specific and based on debt/assets ratio, = 2 if it is firm-specific and based on debt/stock market value ratio); the third x indicates the speed of interest rate adjustment (x3 = 0 if it is slow, = 1 if it is fast); and the fourth x indicates if firms can raise funds in the stock market (by issuing new shares) to finance investment (x4 = 0 if they cannot, = 1 if they can).
The following table shows the level of GNP at the end of a simulation (we have 60 years simulations, where the initial 6 years were used to generate the data for the stock market), and the number of new firms and exits during simulation.
| Experiment | GNP | New firms | Exits |
|---|---|---|---|
| E0000 | 7165 | 132 | 93 |
| E0010 | 7922 | 126 | 98 |
| E0100 | 8579 | 117 | 105 |
| E0110 | 10001 | 111 | 99 |
| E1000 | 5923 | 126 | 137 |
| E1010 | 6113 | 116 | 133 |
| E1100 | 5927 | 156 | 202 |
| E1110 | 5193 | 130 | 100 |
| E1200 | 4446 | 137 | 230 |
| E1210 | 5955 | 129 | 143 |
| E1001 | 9728 | 124 | 141 |
| E1011 | 6394 | 120 | 102 |
| E1201 | 6736 | 122 | 130 |
| E1211 | 5159 | 125 | 124 |
| E2200 | 4136 | 154 | 277 |
| E2210 | 3601 | 192 | 303 |
| E2201 | 5636 | 138 | 191 |
| E2211 | 6220 | 137 | 223 |
Apparently long term GNP growth maximum is attained by combining individual interest rates with fast interest rate adjusatnment (= E0110) compared to the Base case (=E0000), where none of the novel modules are engaged, or when the stockmarket is introduced and can be accessed for investment financing (=E1001). The two maximum performance financial regimes represent very different organizations of financial markets, both however featuring particularly efficient market selections of projects and firms. Whether that efficient selection would be even more efficient if the two regimes are merged (into E1111) is an interesting question that for practical reasons was too late be tested when the simulation results had been studied.
References
-
1
MOSES DatabaseDocumentation of the Planning Survey Data: Cross - Sector and Panel”, Chapter III, MOSES Database, Research Report No. 40. Stockholm, IUI.
- 2
- 3
-
4
Insider Trading, Micro Diversity and the Long-Run Macro EfficiencyWorking Paper No. 355. Stockholm: IUI.
-
5
Learning through short-run macroeconomic forecasts in a micro-to-macro modelJournal of Economic Behavior & Organization 21:181–203.https://doi.org/10.1016/0167-2681(93)90047-S
-
6
The Micro Foundation of Economic Growth301–330, Human Capital, Technological Lock-in and Evolutionary Dynamics, The Micro Foundation of Economic Growth, University of Michigan Press, p.
-
7
Working Papers ERMES 0608, ERMESThe Role Of Commercialization Competence In Endogenous Economic Growth, Working Papers ERMES 0608, ERMES, University Paris 2.
-
8
The Pricing of Options and Corporate LiabilitiesJournal of Political Economy 81:637–654.https://doi.org/10.1086/260062
- 9
-
10
Stochastic behavior of deterministic systemsJournal of Economic Behavior & Organization 16:85–92.https://doi.org/10.1016/0167-2681(91)90044-X
-
11
Teknik Och Industristruktur - 70-Talets Ekonomiska Kris i Historisk BelysningStockholm: IUI and IVA.
-
12
Industrial Subsidies in Sweden: Macro-Economic Effects and an International ComparisonThe Journal of Industrial Economics 32:1.https://doi.org/10.2307/2097983
-
13
Technology and Investment - Crucial Issues for the 1990sProductivity Analysis: A Micro-to-Macro Perspective, Technology and Investment - Crucial Issues for the 1990s, London, Pintner Publishers.
-
14
Technological Systems and Industrial DynamicsNew York: Springer New York.https://doi.org/10.1007/978-1-4615-6133-0
-
15
Technological Systems; Cases, Analyses, ComparisonsMicro-Macro Simulations of Technological Systems, Technological Systems; Cases, Analyses, Comparisons, Boston/Dordrecht/London, Kluwer Academic Publishers, 10.1007/978-1-4615-6133-0.
-
16
The Emergence of Chaos from Classical Economic GrowthThe Quarterly Journal of Economics 98:201.https://doi.org/10.2307/1885621
-
17
Business Economic Planning - Theory, Practice and ComparisonLondon, etc: John Wiley & Sons.
-
18
A Micro-to-Macro Interactive Simulation Model of the Swedish EconomyEconomic Research Report B15. Stockholm: Federation of Swedish Industries. Republished in this Anthology.
-
19
Competition and Market Processes in a Simulation Model of the Swedish EconomyAmerican Economic Review 67:277–281.
-
20
Micro-to-Macro Model of the Swedish EconomyConference Reports, 1978:1. Stockholm: IUI.
-
21
Microeconomic Simulation Models for Public Policy AnalysisExperiments with Fiscal Policy Parameters on a Micro-to-Macro Model of the Swedish Economy, Microeconomic Simulation Models for Public Policy Analysis, Vol, 1 & amp; amp; amp; amp; amp; amp; 2, New York, London, Academic Press. Republished in this Anthology.
-
22
Supplement 2 to the HUS Project, Application to the Swedish Central Bank Centennial FundThe Sophisticated Saver – The Family as a Savings, Investment and Borrowing Institution, Supplement 2 to the HUS Project, Application to the Swedish Central Bank Centennial Fund, Stockholm.
-
23
Policy Making in a Disorderly World Economy, Conference ReportsOn the Optimal Rate of Structural Adjustment, Policy Making in a Disorderly World Economy, Conference Reports, Conference Reports, 1983: 1. Stockholm, IUI.
-
24
Micro heterogeneity of firms and the stability of industrial growthJournal of Economic Behavior & Organization 5:249–274.https://doi.org/10.1016/0167-2681(84)90002-7
-
25
The Firm and Financial Markets in the Swedish Micro-to-Macro Model - Theory, Model and VerificationStockholm: IUI.
-
26
The Dynamics of Market EconomiesA Note on the Stability of Economic Organizational Forms and the Importance of Human Capital, The Dynamics of Market Economies, Stockholm, Amsterdam, IUI, North‑Holland.
-
27
IUI Yearbook 1986‑1987, The Economics of Institutions and MarketsThe Economics of Institutions and Markets - The Organization of Research at IUI, IUI Yearbook 1986‑1987, The Economics of Institutions and Markets, Stockholm, IUI.
-
28
Economic Growth and the Dynamics of Wage Determination - A Micro Simulation Study of the Stability Consequences of Deficient Variation in Factor Prices and Micro StructuresWorking Paper No. 170, Stockholm: IUI. Republished in this Anthology.
-
29
Technological Competition and Trade in the Experimentally Organized EconomyResearch Report No. 32. Stockholm: IUI.
-
30
Expansion, Avveckling Och Företagsvärdering i Svensk IndustriÄgare, Entreprenörer och Kapitalmarknadens Organisation - En Teoretisk Presentation och Översikt;" (Owners, Entrepreneurs and the Organization of the Capital Market – Theoretical Presentation and Survey, Expansion, Avveckling Och Företagsvärdering i Svensk Industri, Stockholm, IUI.
-
31
The firm as a competent teamJournal of Economic Behavior & Organization 13:275–298.https://doi.org/10.1016/0167-2681(90)90002-U
-
32
The Knowledge Based Information EconomyThe Knowledge-Based Information Economy,’ Chapter I, The Knowledge Based Information Economy, Stockholm, IUI.
-
33
Modeling the Experimentally Organized Economy - Complex Dynamics in an Empirical Micro-Macro Model of Endogenous Economic GrowthJournal of Economic Behavior and Organization 16:153–182.https://doi.org/10.1016/0167-2681(91)90047-2
-
34
Deregulation, innovative entry and structural diversity as a source of stable and rapid economic growthJournal of Evolutionary Economics 1:49–63.https://doi.org/10.1007/BF01202338
-
35
Entrepreneurship, Technological Innovation, and Economic Growth: Studies in the Schumpeterian Tradition251–277, Business Competence, Organizational Learning and Economic Growth - Establishing the Smith-Schumpeter-Wicksell Connection, Entrepreneurship, Technological Innovation, and Economic Growth: Studies in the Schumpeterian Tradition, Ann Arbor, University of Michigan Press, p.
-
36
Moses DatabaseThe MOSES Model - Database and Applications, Chapter 1, Moses Database, Research Report No. 40. Stockholm, IUI.
-
37
’The Limits of Policy Making: An Analysis of the Consequences of Boundedly Rational Government Using the Swedish Micro to Macro Model (MOSES)Intermediate Report No. 333, Stockholm: IUI: Republished in this Anthology.
-
38
The Markets for Innovation, Ownership and ControlA Note: On Privatization, Contract Technology and Economic Growth, The Markets for Innovation, Ownership and Control, Stockholm, Amsterdam, IUI, North Holland.
-
39
Beyond Competition - The Future of Telecommunications335–359, The Macroeconomic Effects of New Information Technology, with Special Emphasis on Telecommunications, Beyond Competition - The Future of Telecommunications, Amsterdam, Elsevier Science Publishers, p.
-
40
The Economics of Technical Change - The macroeconomic consequences of business competence in an experimentally organized economyRevue d’Économie Industrielle, Numero Exceptionnel pp. 53–82.
-
41
Firm Objectives, Controls and Organization - the Use of Information and the Transfer of Knowledge within the FirmBoston/ Dordrecht/London: Kluwer Academic Publishers.
-
42
Micro-Simulation and Public PolicyEndogenous Economic Growth through Selection, Micro-Simulation and Public Policy, Amsterdam, North Holland. Republished in this Anthology.
-
43
Spillovers, integrated production and the theory of the firmJournal of Evolutionary Economics 6:125–140.https://doi.org/10.1007/BF01202590
-
44
The biotechnological competence blocRevue d’économie Industrielle 78:7–26.https://doi.org/10.3406/rei.1996.1641
- 45
-
46
From plan to marketsJournal of Economic Behavior & Organization 34:49–68.https://doi.org/10.1016/S0167-2681(97)00051-6
-
47
Telecommunications and Social Economic Development205–217, Information Efficiency, Production Organization and Systems Productivity Quantifying the Systems Effects of EDI Investments, Telecommunications and Social Economic Development, Amsterrdam, North Holland, p.
-
48
The Nature of Economic Change and Management in the Knowledge-Based Information Economy”, KTH, TRITA-IEO-R 1998-19. Published 2005 as, “ The Nature of Economic Change and Management in a New Knowledge Based Information EconomyInformation Economics and Policy 17:428–456.https://doi.org/10.1016/j.infoecopol.2005.02.002
-
49
Dynamik och Flexibilitet i Svensk IT-Industry (Dynamics and Flexibility in Swedish IT-Industry)Stockholm: City University Press.
-
50
Competitiveness and the Value of Intangible Assets42–71, Making Intangibles Visible- The Value, the Efficiency and the Economic Consequences of Knowledge, Competitiveness and the Value of Intangible Assets, Cheltenham, UK & Northampton, USA, Edward Elgar, p.
-
51
Industrial policy, competence blocs and the role of science in economic developmentJournal of Evolutionary Economics 10:217–241.https://doi.org/10.1007/s001910050013
-
52
Generalizing from Cases to Macro, Mimeo, Department of Industrial EconomicsStockholm: KTH.
-
53
Technological Systems in the Bio Industries285–333, The economic potential of biotechnology in agriculture and food production, Mimeo, KTH, Stockholm. Published 2002 as A Competence Bloc Analysis of the Economic Potential of Biotechnology in Agriculture and Food Production, Technological Systems in the Bio Industries, Boston/Dordrecht/London, Kluwer Academic Publishers, p.
-
54
Entrepreneurship. The New Economy and Public Policy91–115, The Markets for Strategic Acquisitions, mimeo KTH Stockholm. Published 2005 as Eliasson, Gunnar & Åsa Eliasson, 2005.”The Theory of the Firm and the Markets for Strategic Acquisitions”, Entrepreneurship. The New Economy and Public Policy, Berlin, Heidelberg, New York, Springer, p.
-
55
Economic Evolution, Learning and Complexity – Econometric, Experimental and Simulation Approaches265–286, Institutions, Entrepreneurship, Economic Flexibility and Growth – Experiments on an evolutionary model, Economic Evolution, Learning and Complexity – Econometric, Experimental and Simulation Approaches, Heidelberg and Munich, Physica Verlag, p.
-
56
The Contribution of Human and Social Capital to Sustained Economic Growth and Well-BeingThe Role of Knowledge in Economic Growth, The Contribution of Human and Social Capital to Sustained Economic Growth and Well-Being, Paris and HRDC, Canada, OECD.
-
57
The Birth, the Life and the Death of Firms- the Role of Entrepreneurship, Creative Destruction and Conservative Institutions in a Growing and Experimentally Organized Economy305–356, Firm Turnover and the Rate of Macroeconomic Growth,Department of Industrial Economics, TRITA series,KTH, Stockholm. Published 2005 as Chapter VI, The Birth, the Life and the Death of Firms- the Role of Entrepreneurship, Creative Destruction and Conservative Institutions in a Growing and Experimentally Organized Economy, Stockholm, The Ratio Institute, Republished in this Anthology, p.
-
58
Modeling Derivatives in a Firm Based Evolutionary Macro Model - the Integration of Computing, Communications and Financial ServicesIndek, TRITA, Stockholm: KTH.
-
59
Electronic Money; New Markets for New Banks, or Markets for Non-BanksStockholm: KTH, INDEK, TRITA IEO-R.
-
60
Information and Organization285–305, Communication, Information Technology and Firm Performance, Information and Organization, North Holland, p.
-
61
Internet Economics and Internet TechnologyThe Internet, Electronic Business and the Euro – on information products, market transparency and Internet economics, Internet Economics and Internet Technology, Stockholm, KTH, TRITA,IEO-R 1999-06.
-
62
A Theory of the Consumption FunctionPrinceton: Princeton University Press.https://doi.org/10.1515/9780691188485
-
63
Technology, Financial Integration, and the Effectiveness of Monetary Policy10, Technology, Financial Integration, and the Effectiveness of Monetary Policy, KTH TRITA-IEO/R, p.
-
64
What do we know about entry?International Journal of Industrial Organization 13:421–440.https://doi.org/10.1016/0167-7187(95)00498-X
-
65
Information Content of Insider Trading Around Corporate Announcements: The Case of Capital ExpendituresThe Journal of Finance 45:835.https://doi.org/10.2307/2328795
- 66
-
67
Portfolio SelectionThe Journal of Finance 7:77–91.https://doi.org/10.1111/j.1540-6261.1952.tb01525.x
- 68
- 69
-
70
The Cost of Capital, Corporate Finance and the Theory of InvestmentAmerican Economic Review 48:261–297.
-
71
The Markets for Innovation, Ownership and ControlInnovative Activity and Venture Financing: Access to Markets and Opportunities in Japan, the US and Europe, The Markets for Innovation, Ownership and Control, Stockholm, Amsterdam, IUI, North Holland.
- 72
-
73
Capital Asset Prices: A Theory of Market Equilibrium under Conditions of RiskThe Journal of Finance 19:425–442.https://doi.org/10.1111/j.1540-6261.1964.tb02865.x
-
74
The investment opportunity set and corporate financing, dividend, and compensation policiesJournal of Financial Economics 32:263–292.https://doi.org/10.1016/0304-405X(92)90029-W
-
75
MOSES on PC: Manual, Initialization, and CalibrationIUI Research Report Nr 39., Stockholm: IUI.
-
76
MOSES on PC: Manual, Initialization, and CalibrationCalibration”, Chapter III, MOSES on PC: Manual, Initialization, and Calibration, IUI Research Report Nr 39., Stockholm, IUI.
-
77
MOSES DatabaseInitial State Dependency – Sensitivity Analyses on MOSES, Chapter VI, MOSES Database, Stockholm, IUI.
-
78
MOSES DatabaseA Description of the Initial 1982 and the Synthetic 1990 Databases. Chapter II, MOSES Database, Stockholm, IUI.
-
79
Modeling the Stock and Derivatives Market in MOSESStockholm: KTH, TRITA - IEO-R 1999-09.
- 80
Article and author information
Author details
Acknowledgements
A study from the project: The Macroeconomic Effects of Computer and Communications Technology,, funded by the Swedish Transport and Communications Research Board in the TRITA series of the department of Industrial Economics at the Royal Institute of Technology (KTH), Stockholm. Because of the extreme demands on computer capacity all simulation experiments technically prepared in this paper and coded in the model have not yet been conducted, notably those on insiders and venture capital. Since the plan is to complete these experiments later when computer. We find that this theoretical presentation is interesting on its own merits because it illustrates the potential for general economic analysis offered by mathematical simulation or microsimulation methods.
Publication history
- Version of Record published: December 2, 2024 (version 1)
Copyright
© 2024, Eliasson and Taymaz
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.


