
Keeping the Best of Two Worlds: Linking CGE and Microsimulation Models for Policy Analysis
Abstract
In this paper, we link a CGE model with the tax-benefit microsimulation model EUROMOD for Latvia. The model linkage is done using an iterative top-down bottom-up approach, ensuring the convergence of changes in disposable income, employment and wage in both models. We also incorporate the unreported wage payments in CGE and EUROMOD to account for the substantial labour tax non-compliance in Latvia and improve the modelling of the fiscal sector. Two simulations demonstrate the advantages of the joint CGE-EUROMOD system over the individual macro and microsimulation models. The lack of income distribution aspect and the scarcity of fiscal instruments in CGE can be overcome by the features of EUROMOD. The CGE model, on the other hand, provides macroeconomic spillovers that are missing in the simulations of EUROMOD.
1. Introduction
The "Evidence-based" approach has become key to government thinking about how new policies are designed and enforced. In this context, computable general equilibrium (CGE) models are an essential tool well-suited for analysing sectoral interdependencies and general equilibrium effects of policy changes or shocks. Such models, however, are less useful when it comes to the analysis of individual-level and distributional effects (see Cockburn et al., 2014; DeBacker et al., 2019; Peichl, 2009). Microsimulation models, on the other hand, are very helpful in accounting for all tax-benefit system complexities and estimating the distributional effects of policy interventions but are not well-suited for modelling their indirect effects, which can be non-negligible in case of large policy shocks (Barrios et al., 2019). Linking these two kinds of models allows using their respective advantages.
There are two general ways of linking the models.1 First, a microsimulation model can be fully integrated into a CGE model, whereby representative households in the CGE model are replaced by the actual households contained in the microsimulation model (see, e.g. Rutherford and Tarr, 2008; Rausch et al., 2011; van Ruijven et al., 2015; Cury et al., 2016). Second, the models can be linked in a "layered" way where the linkage is performed in a specially built interface using a set of linkage variables common to both models. The linkage can work "top-bottom", i.e. the shock is first modelled in CGE and then transferred to the microsimulation model (Bourguignon et al., 2003; Bourguignon et al., 2008; Hérault, 2010; Cockburn et al., 2016; Llambi et al., 2016; Tiberti et al., 2018), or "bottom-up", which involves using the output of the microsimulation model as an input in the CGE model (Benczúr et al., 2018), or in an iterative manner involving numerous rounds of sequential simulations and exchanges of results between the models (Savard, 2003; Savard, 2010).
In this paper, we draw on the example of Latvia and link a CGE model with the Latvian tax-benefit microsimulation model EUROMOD using an iterative top-down bottom-up approach. The information from EUROMOD to CGE (the bottom-up link) is transmitted through the percentage change in nominal household disposable income by income quintiles, budget revenues from labour taxes, and budget expenditures on benefits. The top-down link is implemented via two channels. The first channel transmits changes in labour market participation rate and percentage changes in employment, disaggregated by NACE industries and three skill categories. The second channel works through percentage changes in gross wages by industries and skills, changes in prices, and changes in the share of unreported wages by industries. To translate macro-level changes in employment and wages into the microsimulation model, we follow a regression-based approach similar to Marx et al. (2012) and estimate probabilities to be employed, unemployed, or out of the labour force for each adult individual, and estimate the expected wage for new hires.
Our contribution to the literature is mainly twofold. First, our paper contributes to the still scarce existing literature on macro-micro model linkage. In this paper, we link EUROMOD with a CGE model, while several other recent papers (Barrios et al., 2019; and Barrios et al., 2020) link EUROMOD with dynamic stochastic general equilibrium (DSGE) models. Using a CGE model limits our ability to analyse the dynamic adjustment to a shock, e.g. due to the absence of price and wage rigidity, but allows for a detailed industry-level analysis. Computationally less demanding CGE models have another advantage of making it feasible to run several rounds of iterations until the results of the two models become consistent.
Second, an essential feature of our linked model is that it contains a block for modelling labour tax evasion. Tax evasion is a salient problem in many post-transition economies (for example, see the results in Putniņš and Sauka, 2015; Gavoille and Zasova, 2021; and Benkovskis and Fadejeva, 2022 for Latvia, Paulus, 2015 for Estonia, Bíró et al., 2022 for Hungary). It is, therefore, crucial to explicitly model the interdependence of tax evasion with the effects of policies and shocks as in Lemelin and Savard, 2022. In this paper, labour tax evasion is endogenised in CGE, allowing for industry-specific responses of the prevalence of tax evasion to changes in tax rates and economic activity. In EUROMOD, unreported wages are imputed following the approach proposed by Benkovskis and Fadejeva (2022), which allows for estimating the distributional effects of policies on both reported and total income (see Barrios et al., 2017 for an example of modelling tax evasion in EUROMOD). A simple rule is added to EUROMOD, stating that the total gross wage cannot be lower than the reported gross wage. On top of that, changes in the extent of labour tax evasion are linked in both models.
The EUROMOD is based on the actual EU-SILC income data for 2015–2018. For 2015, the CGE-EUROMOD system is solved using the actual Supply and Use tables (SUT) and EU-SILC data. For years 2016–2018, the CGE-EUROMOD system employs the actual EU-SILC data, but relies on the predicted SUT data using the dynamic nature of the CGE model. Since 2019, EUROMOD also uses the predicted microeconomic data obtained from the joint iterations of the CGE-EUROMOD system.2Figure A1 We use different periods for scenario analysis to better represent the actual tax/benefit policy rules and income levels at the time of the corresponding historical events.
We demonstrate the advantages of using the linked CGE-EUROMOD model by simulating two shocks. First, we simulate the effects of an industry specific shock. In particular, we simulate the shock to financial services related to the closure of a large Latvian bank (ABLV) in February 2018. This triggered many layoffs in the financial sector and caused a large drop in financial services exports and output of the sector as a whole. We use the linked CGE-EUROMOD model to show that this shock had a substantial distributional effect: since wages in the financial services sector are above the national average, the layoffs among top-earning individuals reduced income inequality.
Second, we simulate the effects of an increase in the size and changes in the rules of a lump-sum family benefit, which was implemented in Latvia in January 2022. The direct short-run effect of such policy change is clearly positive, especially for lower income households that enjoy a larger proportional increase in income thanks to this reform. The indirect effect, which is driven by increased consumption, demand and employment is harder to predict. The linked model allows us to simulate both the short-run (direct) and longer-run (indirect) effects: we show that the increase in demand leads to employment growth, which is more pronounced in lower deciles of income distribution, reinforcing the initial progressive effect of the reform.
The paper is structured as follows. Section 2 provides a brief description of EUROMOD and CGE, Section 3 outlines the methodology of linking the models, Section 4 presents the simulation results, and Section 5 concludes.
2. Description of individual models
2.1. EUROMOD
EUROMOD is a tax-benefit microsimulation model covering all EU Member States and the UK (see Sutherland and Figari, 2013), designed to simulate tax liabilities and benefit entitlements at individual and household level.3 The model code describes the policy rules that are in place in each Member State, and which can be easily adjusted to simulate the effects of various policy reforms. EUROMOD is a static model in the sense that it does not account for any possible behavioural responses that may be caused by the reforms, and it also abstracts from any changes in population demographic composition that occur over time; hence the simulated effects of a reform should be interpreted as short-term "overnight" effects.
The model uses two key ingredients: input micro data at individual and household level (EU-SILC in most countries’ models) and the model code describing the national policy rules. Latvian EUROMOD is traditionally based on the EU-SILC data. At the moment of the research the EU-SILC data for 2016–2019 (income years 2015–2018) and corresponding policy rules from the national EUROMOD were available. To do policy scenarios for the later years we adjusted the EU-SILC microdata from 2019 by working-in the changes in macro time series of the corresponding year to the CGE model and then using the output to update the microdata through the joined CGE-EUROMOD system (see Figure A1 in Appendix). The economic status and wages were updated as described in Section 3.4. Policy rules for 2021 were created by updating the corresponding EUROMOD tax and benefit policy rules for 2019.
Simulations of the EUROMOD involve three major steps. First, using information about the relations within the household (e.g. partners, parents, children), the model creates tax-benefit assessment units, which do not necessarily coincide with households. Second, for each individual within the assessment unit, the model assesses his/her eligibility for benefits and taxes, which depends on the composition of the assessment unit and the reported incomes from all sources. Finally, based on the policy rules, the model simulates taxes and benefits for each individual within the assessment unit.
The scope of the Latvian EUROMOD includes direct taxes applied to individual income and cash benefits, thus allowing to simulate individual net income. The model includes personal income tax (PIT), the solidarity tax and mandatory social security contributions (SSC); on the benefit side, it simulates all major child-related benefits, the unemployment benefit and two main means-tested benefits that are paid to the poorest population groups (for more information on the latest version of the Latvian EUROMOD model, see Pluta, 2021).
EUROMOD is widely used for policy analysis in EU Member States, both at the country and EU level. For example Bargain et al. (2014) use EUROMOD for euro area countries to simulate the effect of a fiscal union by imposing a homogenous tax system in the Member States and introducing automatic stabilisation and redistribution mechanisms across countries. Jara Tamayo and Simon (2021) use the model to simulate the effects of a common unemployment insurance system for the Economic and Monetary Union and estimate the effect of such a system on income of atypical workers (part-time workers and workers with temporary contracts). Euromod (2021) estimates distributional effects of all policy changes implemented in 2019–2020 in EU countries and the UK. EUROMOD was also previously used to analyse the distributional impact of selected policy changes in Latvia (see Pluta and Zasova, 2017; and Pluta and Zasova, 2018).
We introduced one modification to the current version of Latvian EUROMOD to facilitate the linkage with the Latvian CGE model that contains both reported and total (including unreported) labour income. Since the gross wage income in the EU-SILC is assumed to be the reported wage,4 estimation of the unreported wages at the individual level was required. Here we follow the recently introduced approach of Benkovskis and Fadejeva (2022), who extended the Gavoille and Zasova (2021) evaluation of the probability of a firm to engage in labour tax evasion by estimating the size of the unreported payments at the employee level.
Unlike Benkovskis and Fadejeva (2022) we do not use matched employer-employee data for the EUROMOD simulations, but the EU-SILC database contains only limited information about the firm where the person is employed (economic sector and the size class only). We re-estimate the main Stochastic Frontier Analysis (SFA) regression of Benkovskis and Fadejeva (2022) using only explanatory variables available in the EU-SILC.5 Although it reduces the set of firm-level variables in the analysis (we do not control for the age, number of employees, or ownership status), the set of employee-level variables remains almost unchanged (including data on education, occupation category, experience, age). The probability of a firm to pay envelope wages is determined by the probit model for the probability of tax evasion from Benkovskis and Fadejeva (2022). This probability is assumed to be homogeneous within an industry-size firm group and used as an input variable in the SFA regression.
The estimated coefficients of the SFA regression are then applied to the EU-SILC data evaluating the potential gross wage for each employee in the EU-SILC.6 The potential (total) gross wage of an individual equals the sum of the reported wage from the EU-SILC and the imputed unreported wage. Finally, a simple rule stating that the total gross wage cannot be lower than the reported gross wage was introduced to the set of policy rules in EUROMOD.
2.2. CGE
The Latvian CGE model used in this study is an extension of Benkovskis et al. (2016) that uses the most recent and detailed SUT and has more elaborate labour market and consumption blocks. The general structure of the model to a large extent follows the MONASH-style models, in particular, a single-country ORANI-G model (Dixon et al., 2013; Horridge, 2014). In this section, we briefly discuss the main features of the model. A detailed description can be found in Benkovskis and Matvejevs (2023).
In the CGE model, all 63 industries have the same three nests production structure. After acknowledging the total demand, an industry determines its need for the intermediate commodity and primary factor aggregates. The first nest assumes the Leontief production function, thus all inputs are demanded proportionally to the total output. The first nest also includes exogenous production technology. At the second nest, all industries substitute between domestic and imported commodities assuming a product-specific constant elasticity of substitution. Also, industries substitute between two primary factors – capital and labour. Similar to the substitution between domestic and imported commodities, the choice between labour and capital is driven by relative costs. The model consists of three types of labour (high-, medium- and low-skilled) at the third nest,7 and industries are able to substitute between those.
The aggregate demand for domestic and foreign commodities comes from nine different users. Industries use domestic and foreign commodities as an intermediate input in the production process. The other eight users are the final users of commodities: domestic private consumption, domestic government consumption (we separate value added tax (VAT) taxable and VAT exempt government consumption), domestic investments (which include private non-housing investments, private housing investments and government investments), exports as well as direct purchases abroad. Most of the final use categories are modelled using the two nest structure.
First, the final user decides on the amount of each composite commodity. This decision is modelled differently depending on the category of the final use. The current version of the model uses the Klein-Rubin utility function allowing for the product-specific income elasticity. Moreover, the private consumption is split into five income quintiles to account for differences in consumption behaviour across the income distribution. Therefore the effect of prices on distributive analyses is the crucial part of the CGE model since the consumption for five disposable income quintiles is modeled separately accounting for different consumption baskets. The nominal government consumption (both VAT taxable and VAT exempt) and investments are set exogenously for any composite commodity, although the government can still substitute between domestic and imported commodities. Latvia’s exports as well as direct purchases of non-residents in Latvia are driven by exogenous foreign demand for the respective commodity. In addition, from the cost minimisation made by non-residents, the export demand is driven by the relative price of domestic commodities to foreign prices.
At the second stage, the choice between domestic and foreign source for a particular commodity is made based on the relative prices and elasticities of substitution. Private consumers decide on the amounts of composite commodities by maximising household utility for a given level of total nominal consumption.
There are three commodity prices in the CGE model: producer, basic and purchaser prices. The basic prices of domestic industry include only input costs of intermediate production, capital and labour. Once basic prices of industries are known, the basic price for a commodity is determined as a weighted industry basic price. Producer prices of domestic and foreign commodities equal basic prices of the respective commodity plus excise tax payments, while the purchaser prices also include the VAT payments. In addition, it is assumed that only a fraction of agents make excise and VAT payments due to the informal economy.
The main focus of the Latvian CGE model is the fiscal sector, with an extended block devoted both to government revenues and expenditures. Government revenues consist of five major parts: SSC, PIT payments, VAT revenues, excise tax revenues, and other revenues. Modelling revenues from labour taxes – PIT as well as an employer’s and employee’s SSC – is now "outsourced" to EUROMOD (see more detailed description in Section 3.1), allowing for more flexibility in simulating progressive tax rates and exemptions. Budget revenues from VAT depend on nominal private and (VAT taxable) government consumption, private housing investments, commodity-specific VAT rate and the share of users paying commodity taxes. All users except exporters are subject to excise tax payments, where the tax rate is commodity-specific and is applied to the volume of commodity use. Excise tax revenues also depend on the share of users paying commodity taxes. The other revenues are modelled as a fixed proportion to nominal GDP.
The government expenditure block contains a pension block. Numerous benefits are obtained from EUROMOD and used as exogenous input into Latvian CGE, e.g. social expenditures on parental benefits, unemployment benefits, sickness benefits, disability pensions, and other social expenditures (see Section 3.1).8 Also, government expenditures include nominal government consumption, nominal government investments, interest payments on government debt and other expenditures. Interest payments are determined by the current level of government debt and nominal interest rate, while the other components are treated as exogenous.
The demand and supply of labour drive the average wage rate in the economy. The demand for labour is determined by industries, while the supply of labour is determined by the demographic factors and activity rate. The real wage is sticky in the short run and flexible in the long run (see Dixon and Rimmer, 2002, p. 357 for more details and discussions). This is ensured by the equation relating changes in the real wage with the deviation of aggregate employment from its natural level. Thus, a negative shock to the demand of labour drives unemployment above its natural level in the short run, but it also reduces the real wage and adjusts unemployment back to the natural level in the long run.
The informal economy and tax evasion are a well documented issue in post-Soviet economies (see, for instance, Putniņš and Sauka, 2015 for the evaluation of the informal economy in the three Baltic States). Including elements of informal economy into the model is essential for an adequate analysis of fiscal policy. The informal economy in the Latvian CGE model refers to labour (personal income and social contributions) and commodity (value added and excise) tax payments. The share of commodity tax evaders (VAT and excise) is commodity specific, while the share of labour tax evaders (PIT and social security) is industry specific.9 The presence of informal economy and labour tax evasion drives the wedge between the reported and total labour income in the CGE model. The share of tax evaders is partially endogenised by assuming that the changes in tax rates and real activity affect the relative size of the informal economy.10
Since SUT tables for Latvia are available only for 2015, thus the CGE-EUROMOD system is solved using the actual SUT and EU-SILC data for 2015. Afterwards, for 2016–2018, the CGE-EUROMOD system employs the actual EU-SILC data, but relies on the predicted SUT data using the dynamic nature of the CGE model (see Figure A1 in Appendix). Since 2019, also EUROMOD uses the predicted microeconomic data: we use the CGE model to obtain the prediction of changes in employment and wage rates by industry, which are then used to adjust the microsimulation database.
3. Linking EUROMOD with the CGE model
Figure 1 schematically describes linking the Latvian EUROMOD and CGE models in the iterative manner (see Savard, 2003 and Savard, 2010 for more examples of the iterative linkage). In the next sections, we provide a step-by-step description of the linked model.
First, we describe how the changes in the distribution of income, e.g. from adjustments in the EUROMOD policy rules, enter the CGE model. In particular, Section 3.1 lists the outputs of EUROMOD which enter the Latvian CGE model as exogenous shocks. Shocks to the CGE model induce responses of all macroeconomic variables (including labour market indicators such as economic status and wage rate, see Section 3.2). Transmitting the changes in industry and skill level employment and wages to the person-level EUROMOD database is a crucial step of the algorithm. Section 3.3 describes the regressions used in assessing the probability of changes in economic status and the expected wage at individual level. Section 3.4 explains how the results of the above-mentioned regressions are used to adjust the EUROMOD database. Changes in the economic status and wage of individuals alter the distribution of income, aggregate disposable income, tax payments, and fiscal benefits. Thus, the initial exogenous shocks to the CGE model are adjusted to match the new output of EUROMOD, and the process continues until both models converge. Section 3.5 describes the consistency of both models and the convergence criteria.
3.1. EUROMOD output as the input to the CGE model
In general, the CGE models lack the income distribution aspect, as well as the necessary degrees of detail to simulate all tax-benefit system complexities and interrelations (see Cockburn et al., 2014; DeBacker et al., 2019; and Peichl, 2009). Thus, the variables related to the household disposable income, benefits and labour taxation are not modelled in the new version of the Latvian CGE model, but are treated as exogenous variables obtained directly from the Latvian EUROMOD model (see Figure 1, the arrow from EUROMOD to CGE).
Changes in nominal disposable income by income quintile are the most important input to CGE obtained from EUROMOD. Any changes in Latvian policy rules related to labour taxation or benefits directly change the simulated disposable income of each household in EUROMOD. Aggregating those changes using household sample weights provides the overall changes in nominal disposable income for the respective quintile, which is used as an exogenous input in disposable income equation in the CGE (see Benkovskis and Matvejevs, 2023). The change in disposable income transmits to the change in private consumption in CGE, affecting the overall economic activity and consequently all variables in the CGE model.11 Thus, any change in the EUROMOD policy rules has a direct effect on the CGE output.
Apart from the disposable income, the CGE model uses other three groups of inputs coming from EUROMOD. One group of inputs is related to the labour tax revenues. The CGE model uses aggregate PIT payments as well as SSC of employers and employees as exogenous inputs obtained from EUROMOD. This allows simulating virtually any changes in labour taxation, including progressive taxation or changes in deductible income.
Another important group of inputs obtained from EUROMOD is related to benefits. EUROMOD has a large number of different household and individual benefits described in its policy rules. We limit the number of exogenous variables from EUROMOD to five: unemployment benefits, sickness benefits, parental benefits, disability pension benefits, and all other benefits (summed together) available in the Latvian EUROMOD model. All benefits are aggregated at the national level using household weights. Old-age pensions are the only major social benefit that is not taken from EUROMOD but is modelled within CGE (see Benkovskis and Matvejevs, 2023 for more details). This is related to the static nature of EUROMOD that does not account for demographic processes and life-time accumulation of pension capital, which makes the overlapping-generation dynamic CGE modelling framework more suitable.
Finally, there is a special type of inputs to CGE from EUROMOD that is activated only in case of specific simulations related to the exogenous changes in distributions of wages or old-age pensions. For instance, a minimum wage hike affects both the distribution and the aggregate level of wages that cannot be captured by the CGE model. These changes in gross nominal wage by skills and industries,12 together with changes in the share of taxpayers by industries are used as additional exogenous variables in the respective equations of CGE.13 Similarly, changes in the minimum old-age pensions can be accounted for by using the changes in the aggregate old-age pensions from EUROMOD as exogenous shocks to the CGE model. In case of no legislative changes affecting the distribution of wages and pensions, such shocks are set to zero.
3.2. CGE output used as input to EUROMOD
EUROMOD does not account for any possible behavioural responses to tax and benefit policies such as changes in labour supply. In CGE-EUROMOD indirect effects of policy change such as labour market reaction is modelled in CGE and then imputed to the EUROMOD database (see Figure 1, the arrow coming from the CGE model).
There are two major blocks of the CGE output used in the EUROMOD simulations.14 First, the CGE model provides employment changes by industry, and participation changes by age and gender. The changes in employment are further disaggregated by three skills categories. This allows adjusting the economic status of individuals in the EUROMOD database. The second block of the CGE output consists of changes in gross wage by industries and skills, as well as changes in the share of unreported wage payments by industries. Using this CGE output, we can alter wages (both reported and unreported) for individuals that remain employed, and assign a wage for newly employed persons in EUROMOD.
3.3. Modelling labour supply and income
Transferring the output of a macroeconomic model to a microsimulation model is not as straightforward as the reverse process: the output of the CGE model is available at the skill level, while EUROMOD requires to adjust the wage level and economic status of individuals and industry.15, 16, Similarly to Marx et al. (2012), we address this issue by including an additional block of equations that transforms the industry and skill-level output of CGE to individual changes in the EUROMOD database (see Figure 1). All regressions are estimated using the EU-SILC data for 2011–2019 (corresponds to the income reference years 2010–2018).
For each adult individual in the EUROMOD database, we predict eight probabilities: probability to be out of the labour force, probability to be unemployed, three probabilities of being employed (as a high-, medium- or low-skilled worker, respectively) and the relative wage for each of the three skill categories. We predict wages as a ratio to the industry average for each skill category, i.e. we assume that an individual’s wage relative to other workers’ wages in the same skill category does not depend on the industry of employment.17
We estimate two models. First, to predict probabilities of employment and non-employment, we use the multinomial logistic regression and estimate a labour supply model with five alternative economic statuses: employed (or self-employed) as a high-, medium- or low-skilled worker, unemployed or inactive (see Table A1 in Appendix).18 We do not distinguish between part-time and full-time jobs for two reasons. First, unlike the EU-SILC data, the CGE model does not contain information on working hours, hence we cannot separate part-time and full-time employment rates on the macro level. Another reason is that the share of part-time workers is relatively low in Latvia (8.9% vs. 18.2% average in the EU in 2020),19 hence this simplification is reasonable. To define the dependent variable, we assume that anyone who has received employment or self-employment income for more than six months during a given year is employed. Anyone who is above the minimum employment age and below the retirement age, who is not in education, not employed and is actively looking for a job is assumed to be unemployed. Others who are not in education are assumed to be inactive. Recipients of old-age pensions and contributory childcare benefits are excluded from the categories of unemployed and inactive persons.
Second, we estimate a Mincer-type income regression to predict the ratio of reported gross wage to the average reported gross wage in the sector, using the Heckman two-stage procedure.20 The sample selection model allows correcting for selection bias, and therefore can be used to impute the hypothetical wage rates for those actually not working on the basis of the observed employees’ wage rates. In the first stage of the two-step Heckman procedure the binary choice of selection model is formulated for the probability of working as an employee as done in Bourguignon et al. (2008).21 The second stage is a log-linear model for the ratio of the monthly gross wage to the average gross wage in the sector. Apart from other socio-economic factors, the dependent variable is modelled as a function of being employed in a high-, medium- or low-skilled position and the number of months per year of part-time and full-time work (see Table A2 in Appendix).
3.4. Adjusting the EUROMOD database
The regressions described above allow creating an algorithm that transforms industry level shocks to changes in labour variables at the individual level. The multinomial logistic model defining the probability of changes in the economic status are used in choosing persons that are hired or fired, while the Mincer-type Heckman income regression determines the wage of the newly employed individuals.
Figure 2 schematically presents the algorithm of changing economic status. If, for example, the CGE model output suggests that 15 low-skilled employees in Agriculture should become unemployed, the algorithm finds 15 low-skilled individuals in the EUROMOD database currently working in Agriculture with the highest probability to be unemployed, and change their status to unemployed. If, on the contrary, the CGE suggests that 15 high-skilled individuals should be hired in the Finance sector, we simply choose 15 unemployed persons with the highest probability to be employed in high-skilled occupation and change their status accordingly. Similarly, the necessary number of persons can transit from being inactive to active (or vice versa) in a respective age group and gender. Note that transition from inactive to employment or from employment to inactive is also possible via the unemployed status (see Figure 2). Moreover, employees can move from one skill or industry to another, depending on the changes in employment suggested by the CGE and probabilities to be employed in the respective skill.

Change of economic status in the EUROMOD database. Note: P(U) denotes the probability to be employed, – probability to be inactive, – probability to be employed in low-skilled occupation, – probability to be employed in medium-skilled occupation, – probability to be employed in high-skilled occupation. corresponds to the conditional probability, e.g. indicates the probability to become unemployed given that the person is currently employed in low-skilled occupation.
Some complications arise in realisation of this algorithm. The EU-SILC database used by EUROMOD contains survey data with a weight attached to every household (and thus also to each individual within a household). This means that every person in EU-SILC represents a different number of individuals in Latvia’s population. If an individual comes from a household with the weight that equals 125 (so this person represents 125 similar people in the population), we may not necessarily want to hire or fire all 125 people (as represented by the weight). To be more delicate in the selection of people to be employed we prefer to use the “splitting up” approach for weights similar to Dekkers and Cumpston (2012),22 therefore more diverse group of people can change their labour status thus improving the reliability of the model results. This approach is especially important for small countries with relatively low number of respondents in the survey and therefore large weights.
First, we expand the EUROMOD database by replacing each household with a weight (household in the database representing households in Latvia’s population) by similar households with equal weight , so that any household in the new dataset represents households in the population. The upper part of Figure 3 provides the example of this step when a household representing 125 households is split into 5 similar households representing 25 households in the population.23 A similar split is applied to all other households in the survey, so we end up with an expanded dataset where each household has an equal weight of 25.24
If the CGE model indicates that 25 people should be hired as low-skilled employees in Agriculture, we only change the economic status for the respective individual within the household (see the lower part of Figure 3). Now we have four households with no changes in status ( to ), and one household whose members experienced a change in economic status (). All households with no changes are joined back together in household that now has a weight of 100 (to reduce the size of the dataset and speed up EUROMOD simulations), so the initial household is now split into the household (with no changes in status) and household (household member employed in Agriculture).
The choice to hire or fire individuals based solely on the probability of being employed or unemployed creates other problems. For instance, it is not clear which individual to choose in case of equal probabilities. This situation will occur more than often due to the weight splitting approach described just above (note that households to are absolutely similar, including the respective probabilities at the individual level). In addition, real-life change in economic status is affected by various stochastic factors. Therefore, we add a random number (following ) to the estimated probability of being employed/unemployed/inactive to avoid determinism and distinguish between similar individuals.
Finally, some nominal adjustments to the EUROMOD database are required. We deal with newly employed persons first: they obtain the wage predicted by the income regression (see Section 3.3).25 Although the wage regression is not industry-specific, it predicts the expected reported wage relative to the industry average wage in the respective skill category, so the absolute reported wage can be easily determined knowing the employment industry. The total gross wage (including unreported payments) is also imputed. The probability of receiving the unreported wage equals the industry- and firm size-specific proportion of the tax evaders, while the size of the unreported wage is set following the approach by Benkovskis and Fadejeva (2022).26
Table 1 reports the main statistics on evaluated unreported wage payments in 2018. Almost 20% of employees are evaluated to receive some unreported payments, although this proportion varies notably by the level of (legal) gross wage – more than 40% of employees were evaluated as tax evaders in the 1st quintile, while this share is negligible among the employees with the highest wage income. The average size of unreported payments is estimated close to 25% relative to the legal gross wage for employees with non-zero unreported payments. This ratio tends to be substantially higher for employees with low legal wage. One should note, however, that the approach by Benkovskis and Fadejeva (2022) accounts only for the under-reported wage, but does not capture unofficially employed workers and does not account for the possibility of under-reported working hours.
Aggregate statistics on evaluated unreported wage payments in 2018
| The share of employees with unreported wage; % | The ratio of unreported wage to legal gross wage for employees with non-zero unreported payments; % | |
|---|---|---|
| Total | 19.2 | 23.3 |
| 1st quintile (based on legal gross wage) | 42.3 | 44.5 |
| 2nd quintile | 37.5 | 23.8 |
| 3rd quintile | 15.3 | 17.6 |
| 4th quintile | 4.4 | 14.9 |
| 5th quintile | 1.5 | 15.9 |
-
Note: Own calculations.
In order to match the growth of reported and total wage in both models, we apply the gross wage adjustment of reported and total wage to all employees of the respective industry and skill after the wage is assigned to the new employees in EUROMOD.
The changes in gross reported nominal wage, housing prices and overall consumer prices obtained from the CGE model are also used to uprate several variables in EUROMOD. For instance, we uprate non-simulated household benefits as well as other non-wage income.
3.5. Convergence of both models
Figure 1 indicates that shocks can be applied to both models either by changing exogenous variables in the CGE model, or/and altering the policy rules in EUROMOD.27 Any of those shocks induce a process. Changes in the CGE labour market output make adjustments to the economic status and labour income at the individual level in EUROMOD, while the changes in disposable income, tax payments and benefits create a new exogenous shock for CGE. We follow Savard (2003) and Savard (2010) and link both models in the iterative manner that requires several rounds of sequential simulations. Unlike some other linkages (e.g. Barrios et al., 2019 and Barrios et al., 2020) we do not stop after a certain number of rounds, but continue the process until the joint system of the two models converge.
The first motivation for the full convergence comes from the richness of the CGE model that allows for a larger number of linkages between the two models. This comes at the cost of a longer convergence process. Figure 4 shows that the difference in changes in the respective variables between the models can still differ by 1 percentage point on average (but maximum deviation can go up to 3 percentage points) after two iterations. Therefore, more iteration rounds are necessary. The second motivation comes from the fact that despite its size, the CGE models tend to be less computationally intensive comparing with the DSGE models (linked with EUROMOD by Barrios et al., 2019 and Barrios et al., 2020). Together with the relatively small size of the Latvian economy and therefore smaller a EU-SILC database, it makes it feasible to run numerous iteration rounds.
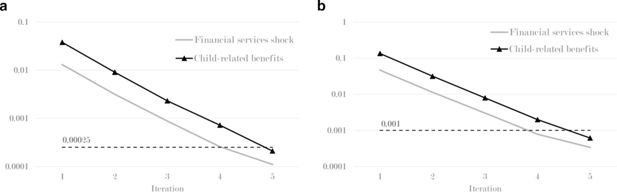
Convergence process of several CGE-EUROMOD simulations. (a) Consistency: root mean square deviation. (b) Consistency: maximum deviation. Note: Own calculations. The "Financial services shock" simulation is described in Section 4.1 and the "Child-related benefits" simulation - in Section 4.2.
To achieve convergence, the models should report consistent results. Since the CGE model output reports changes in economic variables, we require consistency in growth rates rather than levels. The main reason for not controlling for the consistency in levels is very different sources of information used by both models (EU-SILC in EUROMOD and SUT in CGE), which makes our approach different from Barrios et al. 2019 Thus, the consistency of both models is measured by the deviation in growth rates (changes) for several variables in the CGE and EUROMOD models (the respective aggregates are used for EUROMOD). These variables are: the nominal disposable income by quintile, personal income tax payments, social security payments by employees, social security payments by employers, unemployment benefits, parental benefits, sickness benefits, disability pension benefits, and other social benefits. All in all, there are 13 variables that count for the convergence.
We use two criteria that measure the degree of consistency and convergence. First, the root mean square deviation of the growth rate - we require that it should not exceed . Second, since the average measure does not guarantee the absence of large deviations for a single variable, we also use the maximum deviation in growth rates, which is required to be below 0.001 or 0.1 percentage points. Thus, we ensure that the iteration process continues until the changes in the above-mentioned variables are (almost) consistent in both models.
There is hope that the output of both models will become consistent and achieve convergence after a certain number of iterations. However, the complexity of both models does not allow for any theoretical justifications about the existence of convergence. Thus, we can only provide an empirical evidence on how the convergence is achieved. Figure 4 reports the change in the root mean square deviation and the maximum deviation by iteration for three various scenarios. The first scenario is a sectoral shock to the finance industry in the CGE model. The second scenario simulates an increase in child-related benefits in EUROMOD, while the third - imposing a progressive effect of minimum wage change (see Section 4). One thing to notice is that larger shocks tend to require more iterations. Also, despite the convergence process stopping at some level (thus representing the case of non-convergence in the mathematical sense), the deviations between the two models always stabilise at economically negligible level (0.01 percentage point or less) and do not diverge, thus the consistency between the two models is achieved. In general, most of the simulations require about five iteration rounds to converge, which is feasible in terms of computing time.
4. Simulations
In this section we demonstrate advantages of the joint CGE-EUROMOD system by reporting the results of three different simulations. The first simulation shows the results of an industry-specific shock coming from the CGE model. Although this is a usual CGE-style simulation, the CGE-EUROMOD model allows us to assess the impact of such a shock on the distribution of income. The second simulation is related to the changes in the family benefit policy in EUROMOD. We use it to demonstrate the significance of the indirect effects captured by the CGE.
4.1. Scenario 1: Shock to financial services
This is an example of the industry-level shock implemented in the CGE model. The background story of the simulation is the following: ABLV was one of the largest commercial banks in Latvia mostly focused on non-resident business. On 13 February, 2018, the Financial Crimes Enforcement Network of the US Department of Treasury (FinCEN) accused ABLV in suspicion of complicity in money laundering and avoiding currency controls. On 24 February, the European Central Bank announced the liquidation of ABLV, while the shareholders of ABLV made a decision on voluntary liquidation on 26 February. Given that ABLV was heavily involved in non-resident banking business and was the major exporter of financial services, we simulate the liquidation of ABLV as a negative shock to the foreign demand in the respective services. Namely, we reduce the foreign demand by 60% for financial services and by 40% – for auxiliary financial services in 2018.
The shock has a pronounced effect on real output of financial services and auxiliary financial services ( and respectively, see Table 2 for more details on selected Latvian industries) leading to the overall decline in real activity ( for real GDP, see Table A3 in Appendix for the main macroeconomic variables). While the diminishing economic activity negatively affects the industries oriented towards the domestic market (primarily services), the export-oriented industries expand their activity on account of lower wages and improved price competitiveness.
Changes in selected indicators and selected industries in response to the financial services shock simulation (deviation from baseline in 2018; %)
| Variable | Total | Financial services | Auxiliary financial services | Wood production | Construction |
|---|---|---|---|---|---|
| Real output | –0.44 | –13.25 | –3.06 | 0.13 | –0.23 |
| Nominal gross wage | –0.33 | –4.13 | –1.26 | –0.20 | –0.28 |
| Nominal gross wage (high-skilled) | –0.38 | –5.11 | –1.31 | –0.16 | –0.29 |
| Nominal gross wage (medium-skilled) | –0.35 | –3.51 | –0.97 | –0.21 | –0.29 |
| Nominal gross wage (low-skilled) | –0.25 | –1.60 | –0.47 | –0.21 | –0.25 |
| Employment | –0.13 | –12.21 | –2.72 | 0.15 | –0.19 |
-
Note: Own calculations.
Looking at the expenditure side, the decline in activity mainly comes from the diminishing real exports (), while the decline in real private consumption is less pronounced (). Although the shock leads to the decline in employment () and gross real wage (), the negative effect on consumption and activity is subdued due to unemployment benefits. Moreover, the decline in employment and wage mostly affects high- and medium-skilled employees, especially in the financial sector. As a result, the largest losses of disposable income are incurred by rich households (see Figure 5a), limiting the impact on aggregate consumption.
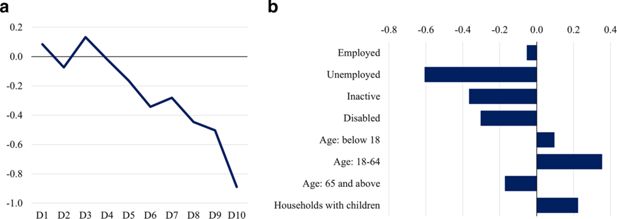
Change in the disposable income (left) and share of at risk of poverty (right). (a) Equivalised disposable income by decile (deviation from baseline; %). (b) At risk of poverty (excluding unreported wages) (deviation from baseline; % points). Note: Own calculations. The income cut points for deciles and median income used for estimation of at risk of poverty threshold (60% of median) are based on the baseline scenario for 2018. The figures show the results of the CGE-EUROMOD model.
The financial services shock also has a negative effect on the fiscal sector. It mainly comes from the revenue side () due to the decline in all major tax revenues, especially PIT revenues. The decline in revenues is also partially explained by a slight increase in tax evasion (can be observed from the wedge between the total and reported gross nominal wage changes), driven by the decline in economic activity.28 Government expenditures are moderately rising due to larger unemployment benefits (), which are now modelled in EUROMOD that captures the increase in the number of unemployed persons.
Although the initial shock comes from the CGE model, the joint CGE-EUROMOD system allows looking into the distributional effects of financial services shock. Figure 5a reveals that the decline in equivalised disposable income is stronger for households from rich income deciles, obviously reflecting higher wages in the financial sector. Despite some spillovers from the financial sector to other industries, the decline in the upper tail of income distribution is also reflected in lower income inequality: the Gini coefficient and the ratio between income in the top and bottom 20 percentiles (S80/S20) decreased ( and , see Table A3 in Appendix). Despite lower inequality, the share of people living in households with equivalised disposable income below 60% of median – so called “at risk of poverty rate” – remained unchanged on average. Figure 5b demonstrates that the highest increase in at risk of poverty measure is observed for working age population and households with children. The share of unemployed and inactive at risk of poverty declines since newly fired people are from relatively wealthy households and therefore the average disposable income of unemployed and inactive increases.
4.2. Scenario 2: Changing family benefits
In this scenario we simulate a change in the state family benefit,29 focusing on the indirect effects of the reform captured by the CGE model. In 2021, the size of the basic benefit for the first child was 11.38 euro per month. For each subsequent child, the benefit was higher: for the second child the benefit equalled the standard amount multiplied by the coefficient of 2, for the third child – multiplied by the coefficient of 3, and for the fourth and each consecutive child – multiplied by the coefficient of 4.4. The size of the supplementary payment was 10 euro per month if there were two dependent children in the family and 66 euro if there were three dependent children in the family. For each subsequent child in the family, the supplementary payment was increased by 50 euro per month.
In 2022, the family benefit reform was implemented. It changed the amount of the state family benefit at the same time waiving the supplementary payment for raising two or more children. The sequential number of the child is not taken into account as of 2022. The family now receives 25 euro per month for one child from one to 20 years of age, 100 euro for two children (50 euro for each child), 225 euro for three children (75 euro for each child). For the family with four children or more, the benefit is 100 euro per month for each child.30 The overall amount of the state family benefit in 2022 increased preserving the idea of much larger benefits for families with many dependent children (see Table 3).
Family benefit by number of dependent children ( euro per month)
| Year | Family with 1 dependent child | Family with 2 dependent children | Family with 3 dependent children | Family with 4 dependent children |
|---|---|---|---|---|
| 2021 | 11.38 | 44.14 | 122.90 | 229.8 |
| 2022 | 25.00 | 100.00 | 225.00 | 400.00 |
-
Note: Own calculations. We assume that in 2021 the sequential number of children corresponds to the actual number of dependent children in a family.
The year 2021 is used as a baseline in this scenario, so in the simulation we apply the 2022 family benefit rules to the 2021 system. The change in policy is financed by expanding the fiscal deficit, which increases by 0.06 percentage points to GDP. Comparing to the actual 2021 policy, the total amount of the family benefit increases by and social expenditures by (see Table A3 in Appendix) if 2022 rules were applied. Increasing the amount of the family benefit primarily affects real private consumption (), which further stimulates the overall activity, and the real GDP grows by .31 The increase in family benefit affects wages and employment indirectly via two channels: first, higher disposable income drives increase in the private consumption, this tightens the labour market by driving up the demand for labour and rising wages; second, higher wages lower competitiveness on the external markets, therefore export declines and pressure on labour demand and wages reduces. The first effect dominates in the domestic market oriented sectors and services, while the second effect restricts rise of employment and wages in the exporting sectors. On average, the employment increases by (almost uniformly for all skills), while the gross nominal wage by (by for the gross legal wage, so the share of tax payers increases due to higher economic activity). Extra social benefits lead to higher government revenues generated from all major taxes, primarily from VAT () due to higher consumption. As a result, the overall effect on the budget balance is almost neutral () despite growing social expenditures.
Linking EUROMOD with the CGE model allows studying the macroeconomic effects of the benefit reform. Even more, we can compare the first-round change in disposable income, i.e. the output from stand-alone EUROMOD, with the overall changes in disposable income, i.e. the output of CGE-EUROMOD model accounting for macroeconomic spillovers. The changes in disposable income in EUROMOD show the effect of higher benefits assuming all other factors constant. The CGE-EUROMOD model, however, accounts for higher employment and wages due to the new family benefit scheme and increased activity (see Figure 6).
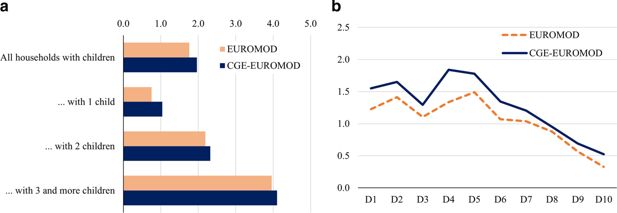
Changes in equivalised disposable income (deviation from baseline; %). (a) By number of children. (b) By decile of equivalised disposable income. Note: Own calculations. Income cut points for deciles are based on the baseline scenario for 2021 and are constant across models.
The equivalised disposable income increases more for families with a larger number of children, according to Figure 6a. Moreover, by comparing the results of stand-alone EUROMOD and joint CGE-EUROMOD system, we see a positive indirect effect on disposable income for households with children stemming from the higher economic activity level. The importance of this indirect effect appears even more obviously in Figure 6b – households from all income groups enjoy the additional positive effect of increasing employment and wages. The positive indirect effect tends to be higher for relatively poor households which consist of a larger share of unemployed persons: changing the status from unemployed to employed substantially increases their disposable.
A stronger rise in the income for low income groups (both due to a higher direct effect of the benefit and stronger macroeconomic spillovers) results in lower inequality measures, i.e. the Gini coefficient declines by , while S80/S20 ratio – by (see Table A3 in Appendix).
5. Conclusions
In this paper, we propose a novel approach to link the CGE model with the tax-benefit EUROMOD microsimulation model. We use the example of Latvia and link the models using the iterative top-down bottom-up approach. The information from EUROMOD to CGE (the bottom-up link) is transmitted through the percentage change in nominal household equivalised disposable income (by quintiles), budget revenues from labour taxes and budget expenditures on benefits. The top-down link consists of changes in the labour market status and gross wages, which are translated into the microsimulation model following a regression-based approach.
We also incorporate the unreported wage payments in CGE and EUROMOD to account for the substantial labour tax non-compliance in Latvia and improve the modelling of the fiscal sector. Labour tax evasion is endogenised in CGE, allowing for industry-specific responses of the prevalence of tax evasion to changes in tax rates and economic activity. In EUROMOD, unreported wages are imputed following the approach proposed by Benkovskis and Fadejeva (2022), which allows for estimating the distributional effects of policies on both reported and total income. A simple rule is added to EUROMOD, stating that the total gross wage cannot be lower than the reported gross wage. Changes in the extent of labour tax evasion are linked in both models.
Linking the two models addresses some drawbacks of the stand-alone versions of CGE and EUROMOD. The lack of income distribution aspect and the scarcity of fiscal instruments in CGE can be overcome by the features of EUROMOD – a tax-benefit miscrosimulation model. The CGE model, on the other hand, provides macroeconomic spillovers that are missing in the simulations of EUROMOD. The newly created joint CGE-EUROMOD system is an extremely rich policy simulation tool analysing a wide spectrum of macroeconomic, industry-specific, fiscal or income distribution shocks.
Our paper demonstrates three examples of possible policy simulations, highlighting the advantages of the joint system. In particular, we show that the capabilities of the CGE model become wider, and one can now observe the income distributional effects for various macroeconomic or industry-specific shocks. Second, the simulation of tax or benefit adjustments now also accounts for changes in the macroeconomic environment, providing more adequate understanding of the overall effect. In addition to the usual advantages of the CGE and EUROMOD models, our system includes the endogenised informal wage section, which allows more realistic modelling of policy measures related to the fiscal sector.
Footnotes
1.
1
For a review of the existing methods, see Peichl (2009), Peichl (2016), Cockburn et al. (2014) and Colombo (2018).
2.
2
see Figure A1 in Appendix for the iterative sequence scheme.
3.
3
More information can be found on the official EUROMOD web page: https://euromod-web.jrc.ec.europa.eu/.
4.
4
The source of employment income in Latvian SILC is a mixture of administrative records and interviews. The exact source for each individual is, however, not documented in SILC flag variables. Latvian baseline EUROMOD version is based on the assumption that the employment income comes from administrative records and hence represents the reported income only. The validity of this assumption is verified by comparing distribution of gross annual wages from SILC and administrative records.
5.
5
For that, similarly to Benkovskis and Fadejeva (2022), we use the employer-employee dataset provided by the State Revenue Service and Central Statistical Burea of Latvia, augmented by the Labour Force Survey database from the Central Statistical Burea of Latvia.
6.
6
See more details about the methodology in Benkovskis and Fadejeva (2022). The coefficients of the SFA equation used to evaluate the potential gross wage in the EU-SILC database are available upon request.
7.
7
The skills are defined corresponding to the major occupation groups, further aggregated into high- (ISCO-08 major groups 1, 2, 3), medium- (0, 4, 6, 7), and low-skilled labour (5, 8, 9).
8.
8
Not all of these benefits are simulated in EUROMOD, e.g. sickness benefits and disability pensions are included in Latvian EUROMOD, but are not simulated.
9.
9
The level of labour and commodity tax evasion was calibrated to match the SUT tax base with the actual tax revenues, given the tax rates. Thus, the share of users paying VAT and excise tax was calibrated to 80% for all commodities in 2015 (for food, alcohol and tobacco – close to 70%). Similarly, the share of enterprises paying labour taxes was calibrated at the broad industry level, ranging between 70% and 98% in 2015.
10.
10
The elasticities are calibrated following Schneider et al. (2010) and expert judgements. An increase in labour tax by 1 percentage point boosts the share of unreported wages by 0.05 percentage points, an increase in effective commodity tax by 1 percentage point enlarges the share of commodity tax evaders by 0.05 percentage points, while growth in real activity by 1% diminishes the share of tax evaders by 0.44 percentage points (see Benkovskis and Matvejevs, 2023, eq. A88-A91 for more details).
11.
11
We make no adjustments to the level of disposable income in EUROMOD, which differs from national accounts. Only changes in disposable income are harmonised between the two models.
12.
12
The Latvian CGE model has 63 two-digit industries, so the changes in the respective exogenous variables are assumed to be equal within the 12 broad industries used by EUROMOD.
13.
13
Note that shocks like minimum wage changes also affect the share of unreported wage payments by decreasing the gap between the total and reported gross wage for individuals affected by the legislative changes. Benkovskis and Fadejeva (2022) demonstrate that the share of employees with unreported wages is especially high when the reported wage is close to the minimum wage.
14.
14
In principle, it is also possible to use the demographic output of CGE to adjust the EUROMOD database (accounting for the newborn children, deceased persons and migration). However, such additional link would not affect much the output of the simulations in the short to medium run, and we limited the linkage to the labour market for simplicity.
15.
15
We define skills in the same way both for the CGE and EUROMOD. Ten major groups of occupations in ISCO-08 are arranged on three skill levels (high, medium and low) on the basis of ILOSTAT approach with minor adjustments to the Latvian labour market. Services and Sales Workers (group 5), Plant and Machine Operators and Assemblers (group 8), Elementary Occupations (group 9) correspond to the the low skill level; Armed Forces Occupations (group 0), Clerical Support Workers (group 4), Skilled Agricultural, Forestry and Fishery Workers (group 6) and Craft and Related Trades Workers (group 7) correspond to the medium skill level; Managers (group 1), Professionals (group 2), Technicians and Associate Professionals (group 3) correspond to the high skill level. In ILOSTAT Armed Forces (group 0) correspond to all three skill levels. Groups 5 and 8 – Services and Sales Workers (group 5), Plant and Machine Operators and Assemblers (group 8) – correspond to the medium skill level.
16.
16
Although CGE works with 63 2-digit industries, EUROMOD only consists of 12 broad sectors, so the output of the CGE is aggregated respectively. Thus the CGE output contains 36 industry and skill-level changes in employment, gross wage and share of tax evaders that should be transformed into individual changes for the EUROMOD.
17.
17
This is a very strong assumption made for the simplicity of the algorithm. In particular, we lack the detailed information on education, experience and qualification that would allow evaluating the eligibility of newly hired employees for a certain industry. In addition, our algorithm implicitly assumes same wage distributions for the respective skills within different industries. This assumption can be relaxed in future versions of the model.
18.
18
The other empirical strategy to determine the probability of employment could be to use the top-down behaviour microsimulation toolkit for distributive analysis developed by Tiberti et al. (2018), which takes into account the probability to be employed of the household head and the occupational choice of the other household members.
19.
19
This difference is mainly due to a higher proportion of women in part-time employment in EU countries (11.3% of employed women in Latvia and 29.6% in the EU). The proportion of men employed part time in Latvia and EU countries is very similar (6.5% of employed men in Latvia vs. 8.4% in EU countries).
20.
20
The top-down behaviour microsimulation toolkit for distributive analysis developed by Tiberti et al. (2018) additionally allows for modelling the income from self-employment activities collected at the household level.
21.
21
The list of selection variables affecting employment probability, but not wages include household non-employment income (per household member), earnings of other household members(per household member), binary variable if paying mortgage, number of children under 3 years of age, and binary variable for disabled person in the household.
22.
22
This is not the only possible approach. One could also take an advantage of the non-binary nature of employment variables in EUROMOD and adjust the number of months spent in employment and unemployment accordingly. Although this would facilitate the algorithm, the major drawback is the absence of skill and industry dimension. The “splitting up” approach allows different persons from the same “original” observation to be employed in different skills and industries. This would not be possible to realise in the latter case, when the number of months spent in employment is altered.
23.
23
We do not split into 125 similar households representing 1 household in the population to reduce the computation burden for EUROMOD. The n = 25 was a compromise between the computation speed and fine granularity in the simulations.
24.
24
Obviously, rounding is applied to some weights in the original database.
25.
25
People who changed their status to unemployed or inactive get zero gross wage income.
26.
26
We follow the classification of the EU-SILC and split firms into four size groups: 10 employees or less, 11 to 20 employees, 21 to 50 employees, more than 50 employees.
27.
27
The iteration always starts from the CGE model. In case the shock is applied only to EUROMOD, we start by running the CGE model with zero exogenous shocks and then proceed to EUROMOD.
28.
28
The size of the informal economy is endogenised in the Latvian CGE model, and declining economic activity in a respective sector increases tax evasion. See last paragraph of Section 2.2, or Benkovskis and Matvejevs (2023) for more details.
29.
29
In the 2021 version of EUROMOD, the family benefit consists of two parts: there is a basic benefit paid to all families with children and supplementary payments, which are paid only to families with two and more dependent children. When calculating the amount of the benefit, the number of children is determined taking into account all children raised by the recipient, even if some of them are no longer dependent. The amount of the benefit is determined by the child’s sequential number in the family according to the birth date, e.g. if there is one adult child in a family and one child below the age of 15, the child aged below 15 is treated as the second child (see Pluta, 2021 for more details on the family benefit modelling in EUROMOD prior to 2022).
30.
30 Law on State Social Allowances, https://likumi.lv/ta/en/en/id/68483.
31.
31
Another way to look at the effect of increased family benefit on the economic activity is to calculate the fiscal multiplier. According to our model it equals 1.6, namely one additional euro of family benefits adds 1.6 euro to nominal GDP. The direct comparison of this number with other estimates of the fiscal multiplier is problematic, since the literature on fiscal multipliers focus on taxes as well as government consumption and investments. Only few studies investigate comparable fiscal multipliers. Al-Eyd and Barrell (2005) use NiGEM model and report the fiscal multiplier for transfers in the range of 0.2-0.6 for various European countries, while Coronado et al. (2005) report the multiplier of 0.3 for the increased child credit in the US. Our estimate exceeds previously reported numbers substantially. This can be explained by the specifics of the CGE model that reports the medium-run response, while previously mentioned estimates refer to the immediate effect within one-two years.
Appendix A
Multinomial logistic regression
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
| Men | Men | Men | Men | Women | Women | Women | Women | |
| Variables | Low-skilled | Medium-skilled | Unemployed | Inactive | Low-skilled | Medium-skilled | Unemployed | Inactive |
| Secondary education | –1.612*** | –1.669*** | –2.251*** | –2.339*** | –1.098* | –0.207 | –2.155*** | –2.619*** |
| Tertiary education | –4.405*** | –4.264*** | –4.769*** | –4.967*** | –4.268*** | –2.471*** | –4.603*** | –5.142*** |
| Age | –0.068*** | –0.068*** | –0.124*** | –0.266*** | –0.049*** | –0.057*** | –0.105*** | –0.212*** |
| Age2 | 0.001*** | 0.001*** | 0.002*** | 0.003*** | 0.001*** | 0.001*** | 0.001*** | 0.002*** |
| Cities other than Riga | 0.441*** | 0.410*** | 0.472*** | 0.489*** | 0.097** | 0.028 | 0.456*** | 0.141*** |
| Thinly populated area | 0.636*** | 0.506*** | 0.772*** | 0.855*** | –0.070* | –0.194*** | 0.405*** | 0.320*** |
| Married | –0.262*** | –0.153*** | –0.701*** | –0.831*** | –0.142*** | –0.078* | 0.006 | 0.241*** |
| Household non-employment income, per household member, in logs | 0.028*** | 0.034*** | 0.028** | 0.059*** | –0.007 | –0.010 | –0.032*** | 0.003 |
| Earnings of other household members, per household member, in logs | –0.034*** | –0.066*** | –0.171*** | –0.158*** | –0.019*** | –0.003 | –0.126*** | –0.065*** |
| Number of children under 3 years of age | –0.112* | –0.067 | –0.788*** | –0.656*** | –0.015 | –0.199** | 1.087*** | 1.107*** |
| Disabled | 0.917*** | 0.170 | 3.153*** | 4.945*** | 0.839*** | 0.749** | 3.313*** | 4.879*** |
| Paying mortgage | –0.512*** | –0.560*** | –0.869*** | –0.819*** | –0.478*** | –0.458*** | –0.614*** | –0.478*** |
| Constant | 3.363*** | 3.514*** | 5.567*** | 7.843*** | 3.264*** | 1.945** | 5.276*** | 7.517*** |
| Observations | 33’055 | 33’055 | 33’055 | 33’055 | 36’220 | 36’220 | 36’220 | 36’220 |
| Years | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
-
*** p<0.01, ** p<0.05, * p<0.1.
-
Note: Own calculations. Data used is EU-SILC 2011-EU-SILC 2019, Latvia. High-skilled is base outcome of the multinomial logistic regression.
Heckman selection model
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Men | Men | Women | Women | |
| Variables | Relative wage in logs | Selection model | Relative wage in logs | Selection model |
| Secondary education | 0.348*** | 0.387*** | 0.443*** | 0.495*** |
| Tertiary education | 0.521*** | 0.669*** | 0.566*** | 0.806*** |
| Medium-skilled | 0.173*** | –0.036 | 0.124*** | –0.021 |
| High-skilled | 0.355*** | 0.241*** | 0.289*** | 0.314*** |
| Age | 0.041*** | 0.003 | 0.014*** | 0.027*** |
| Age2 (*1000) | –0.525*** | –0.227** | –0.177*** | –0.417*** |
| Cities other than Riga | –0.088*** | –0.051 | –0.159*** | –0.079*** |
| Thinly populated area | –0.068*** | –0.227*** | –0.148*** | –0.198*** |
| Married | 0.089*** | 0.227*** | 0.008 | –0.217*** |
| Household non-employment income, per household member, in logs | – | –0.010 | – | –0.010* |
| Earnings of other household members, per household member, in logs | – | 0.101*** | – | 0.062*** |
| Paying mortgage | – | 0.472*** | – | 0.134*** |
| Number of children under 3 years of age | – | 0.253*** | – | –0.911*** |
| Disabled | – | –1.003*** | – | –1.044*** |
| Number of months spent in full-time work | 0.085*** | – | 0.098*** | – |
| Number of months spent in part-time work | 0.015*** | – | 0.034*** | – |
| Constant | –2.223*** | 0.500** | –2.033*** | –0.024 |
| atanh() | –0.411*** | – | –0.474*** | – |
| ln() | –0.486*** | – | –0.392*** | – |
| Observations | 24’477 | 24’477 | 28’384 | 28’384 |
| Years | Yes | Yes | Yes | Yes |
-
*** p<0.01, ** p<0.05, * p<0.1.
-
Note: Own calculations. Data used is EU-SILC 2011–EU-SILC 2019, Latvia. Dependent variable in wage equation is employment income relative to the industry average (in logs).
Changes in selected macroeconomic, fiscal and income distribution variables in response to two scenarios (deviation from baseline; %).
| Variable | Scenario 1: Shock to financial services | Scenario 2: Changing family benefits |
|---|---|---|
| Macroeconomic variables | ||
| Real GDP | –0.44 | 0.28 |
| Real private consumption | –0.17 | 0.81 |
| Real investments | –0.42 | 0.26 |
| Real exports | –0.70 | –0.13 |
| Real imports | –0.25 | 0.30 |
| GDP deflator | –0.22 | 0.15 |
| Consumption deflator | –0.16 | 0.11 |
| Export deflator | –0.12 | 0.08 |
| Import deflator | 0.00 | 0.00 |
| Unemployment (percentage points) | 0.09 | –0.07 |
| Employment | –0.13 | 0.10 |
| Employment (high-skilled) | –0.17 | 0.09 |
| Employment (medium-skilled) | –0.20 | 0.13 |
| Employment (low-skilled) | –0.04 | 0.10 |
| Gross real wage | –0.17 | 0.09 |
| Gross nominal wage | –0.33 | 0.20 |
| Gross nominal wage (high-skilled) | –0.38 | 0.19 |
| Gross nominal wage (medium-skilled) | –0.35 | 0.21 |
| Gross nominal wage (low-skilled) | –0.25 | 0.20 |
| Gross nominal reported wage | –0.44 | 0.26 |
| Fiscal variables | ||
| Budget balance (percentage points to GDP) | –0.28 | –0.06 |
| Budget expenditures | 0.10 | 0.65 |
| Social expenditures | 0.31 | 2.58 |
| Old-age pensions | –0.02 | 0.02 |
| Disability pensions | 0.00 | 0.00 |
| Sickness benefits | 0.00 | 0.00 |
| Unemployment benefits | 5.72 | 0.07 |
| Family-related benefits | 0.00 | 14.39 |
| Other benefits | 0.04 | –0.15 |
| Budget revenues | –0.65 | 0.50 |
| Social security contribution revenues | –0.64 | 0.30 |
| Personal income tax revenues | –0.97 | 0.37 |
| Value added tax revenues | –0.54 | 0.96 |
| Excise tax revenues | –0.39 | 0.55 |
| Income distribution (EUROMOD-CGE) | ||
| Gini coefficient (equivalised total disposable income) | –0.25 | –0.44 |
| Gini coefficient (equivalised reported disposable income) | –0.32 | –0.48 |
| S80/S20 (equivalised total disposable income) | –0.01 | –0.65 |
| S80/S20 (equivalised reported disposable income) | –0.11 | –0.85 |
-
Notes: Own calculations. Baseline for Scenario 1 is the year 2018, for Scenario 2 - the year 2021.
References
-
1
Estimating tax and benefit multipliers in EuropeEconomic Modelling 22:759–776.https://doi.org/10.1016/j.econmod.2005.05.005
-
2
Fiscal union in Europe? redistributive and stabilizing effects of a European tax-benefit system and fiscal equalization mechanismEconomic Policy 28:375–422.https://doi.org/10.1111/1468-0327.12011
-
3
Working Paper on Taxation and Structural Reforms 2017-05. Joint Research CentreWorking Paper on Taxation and Structural Reforms 2017-05. Joint Research Centre.
-
4
Dynamic scoring of tax reforms in the european unionJournal of Policy Analysis and Management 38:239–262.https://doi.org/10.1002/pam.22105
-
5
Progressive tax reforms in flat tax countriesEastern European Economics 58:83–107.https://doi.org/10.1080/00128775.2019.1671201
-
6
Assessing the economic and social impact of tax and benefit reforms: A general-equilibrium microsimulation approach applied to HungaryEconomic Modelling 75:441–457.https://doi.org/10.1016/j.econmod.2018.06.016
- 7
- 8
- 9
-
10
The minimum wage, informal pay, and tax enforcementJournal of Public Economics 215:104728.https://doi.org/10.1016/j.jpubeco.2022.104728
-
11
Working Paper DT/2003/10, DIAL (Développement, Institutions et MondialisationWorking Paper DT/2003/10, DIAL (Développement, Institutions et Mondialisation.
-
12
The Impact of Macroeconomic Policies on Poverty and Income Distribution: Macro-Micro Evaluation Techniques and Tools93–118, Examining the social impact of the indonesian financial crisis using a macro-micro model, The Impact of Macroeconomic Policies on Poverty and Income Distribution: Macro-Micro Evaluation Techniques and Tools, England, Palgrave-Macmillan Houndmills, p.
-
13
Handbook of Microsimulation Modelling275–304, Macro-micro models, Handbook of Microsimulation Modelling, Vol, 293, Emerald Group Publishing Limited, p, 10.1108/S0573-85552014293.
-
14
Fiscal space and public spending on children in burkina fasoInternational Journal of Microsimulation 9:5–23.https://doi.org/10.34196/ijm.00126
-
15
Linking CGE and microsimulation models: A comparison different approachesInternational Journal of Microsimulation 3:72–91.https://doi.org/10.34196/ijm.00026
-
16
Finance and Economics Discussion Series 2005-32, Board of Governors of the Federal Reserve System (U.S)Finance and Economics Discussion Series 2005-32, Board of Governors of the Federal Reserve System (U.S).
-
17
Cash transfer policies, taxation and the fall in inequality in Brazil an integrated microsimulation-CGE analysisInternational Journal of Microsimulation 9:55–85.https://doi.org/10.34196/ijm.00128
-
18
Integrating microsimulation models of tax policy into a DGE macroeconomic modelPublic Finance Review 47:207–275.https://doi.org/10.1177/1091142118816744
-
19
On weights in dynamic-ageing microsimulation modelsInternational Journal of Microsimulation 5:59–65.https://doi.org/10.34196/ijm.00072
-
20
Contributions to Economic Analysis256, Dynamic general equilibrium modelling for forecasting and policy: a practical guide and documentation of MONASH, Contributions to Economic Analysis, North-Holland, Elsevier, 10.1108/S0573-8555(2001)256.
-
21
Handbook of Computable General Equilibrium Modeling23–103, The MONASH style of computable general equilibrium modeling: a framework for practical policy analysis, Handbook of Computable General Equilibrium Modeling, Elsevier, p.
- 22
- 23
-
24
Sequential linking of computable general equilibrium microsimulation models: A comparison of behavioural reweighting techniquesInternational Journal of Microsimulation 3:35–42.https://doi.org/10.34196/ijm.00023
- 25
- 26
-
27
What do CGE models have to say about fiscal reform?Economic Analysis and Policy 74:758–774.https://doi.org/10.1016/j.eap.2022.04.003
-
28
Assessing the impacts of a major tax reform: A CGE-microsimulation analysis for UruguayInternational Journal of Microsimulation 9:134–166.https://doi.org/10.34196/ijm.00131
-
29
Can higher employment levels bring down relative income poverty in the EU? regression-based simulations of the Europe 2020 targetJournal of European Social Policy 22:472–486.https://doi.org/10.1177/0958928712456577
-
30
Working Paper 2015-10, Institute for Social and Economic ResearchWorking Paper 2015-10, Institute for Social and Economic Research.
-
31
The benefits and problems of linking micro and macro models — evidence from a flat tax analysisJournal of Applied Economics 12:301–329.https://doi.org/10.1016/S1514-0326(09)60017-9
-
32
Linking microsimulation and CGE modelsInternational Journal of Microsimulation 9:167–174.https://doi.org/10.34196/ijm.00132
- 33
- 34
-
35
EUROMOD Country report, EUROMOD at the Institute for Social and Economic ResearchEUROMOD Country report, EUROMOD at the Institute for Social and Economic Research.
-
36
Measuring the shadow economy using company managersJournal of Comparative Economics 43:471–490.https://doi.org/10.1016/j.jce.2014.04.001
-
37
Distributional impacts of carbon pricing: A general equilibrium approach with micro-data for householdsEnergy Economics 33:S20–S33.https://doi.org/10.1016/j.eneco.2011.07.023
-
38
Poverty effects of Russia’s WTO accession: Modeling “real” households with endogenous productivity effectsJournal of International Economics 75:131–150.https://doi.org/10.1016/j.jinteco.2007.09.004
- 39
-
40
Scaling up infrastructure spending in the philippines: A CGE top- down bottom-up microsimulation approachInternational Journal of Microsimulation 3:43–59.https://doi.org/10.34196/ijm.00024
-
41
New estimates for the shadow economies all over the worldInternational Economic Journal 24:443–461.https://doi.org/10.1080/10168737.2010.525974
-
42
EUROMOD: the European union tax-benefit microsimulation modelInternational Journal of Microsimulation 6:4–26.https://doi.org/10.34196/ijm.00075
-
43
A top-down with behaviour (TDB) microsimulation toolkit for distributive analysisInternational Journal of Microsimulation 11:191–213.https://doi.org/10.34196/ijm.00185
-
44
Methods for including income distribution in global CGE models for long-term climate change researchEnergy Economics 51:530–543.https://doi.org/10.1016/j.eneco.2015.08.017
Article and author information
Author details
Funding
Anna Pluta and Anna Zasova gratefully acknowledge funding from research project No. LB-07/2018/53 "Merging Latvian EUROMOD with the Bank of Latvia's CGE model" commissioned by the Bank of Latvia in 2018-2019.
Publication history
- Version of Record published: April 30, 2024 (version 1)
Copyright
© 2024, Beņkovskis et al.
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.





