1. Pensions and retirement
  2. Demography
Download icon

Partition of the Life Course: An Extended Dynamic Microsimulation Analysis

  1. Janne Salonen  Is a corresponding author
  2. Heikki Tikanmäki
  3. Sampo Lappo
  1. Keva, Finland
  2. Finnish Centre for Pensions, Finland
Research article
Volume 14(3) Winter 2021
Cite this article as: J. Salonen, H. Tikanmäki, S. Lappo; 2021; Partition of the Life Course: An Extended Dynamic Microsimulation Analysis; International Journal of Microsimulation; 14(3); 54-75. doi: 10.34196/ijm.00241

Abstract

This study explores life courses in a dynamic microsimulation framework at a time of high public interest in prolonging working lives. We provide new insights into how historical records could be merged with microsimulation outcomes and develop a new indicator for measuring and illustrating individual life course stages in adulthood. Partition of the life course yields the average lengths of life course stages in Finland. We illustrate our indicator and its distribution by gender, cohort and level of education. The proposed indicator is also used to elaborate widely accepted indicators from the Pension Adequacy Report. We conclude that the proposed partitioning method should be easily transferrable to other countries where historical records are available.

1. Introduction

EU institutions regularly publish calculations and projections of the sustainability of public finances. The Economic Policy Committee’s working group on ageing populations and sustainability (AWG) systematically monitors ageing trends with a focus on finances (e.g. EU AWG, 2018), while the Social Protection Committee (SPC) takes a special interest in the social sustainability of ageing. For some time now there has been a drive across Europe to try and prolong working lives and postpone retirement. Pension and labour market policies have been geared to reduce early retirement opportunities, raise pensionable ages, introduce tighter eligibility criteria and to support employment in the ageing workforce (see OECD, 2019a; EU EPC, 2020; EU AWG, 2021; European Commission, 2021. Overall, there is greater public awareness about the problems associated with increasing life expectancy. 1

In most European countries, social security accounts for a major part of public finances and public expenditures. The single biggest public expenditure item is pension spending. Population ageing has thrust the sustainability of pension schemes firmly into the spotlight. Social transfers and expenditures are ultimately covered from tax revenue collected from businesses and working age individuals. The length of active working life and financially meaningful employment are therefore of paramount interest. But how to measure the length of employment and retirement during the life course in a simple and tractable way, and what is the value added of using simulation techniques to analyse and visualize their respective shares?

Established measures and indicators of employment and retirement are usually based on statistics and ad hoc calculations. All these measures have their pros and cons. Statistics are collected and compiled in a relatively uniform manner across countries, but their substantive contents or time span are often limited. One example of a much used statistical indicator is the employment rate. Employment rates for employees aged 55–59, 60–64 and 65–69, for instance, give an overview of late career employment trajectories (e.g. OECD, 2019a). Reform success, then, can be assessed by monitoring retirement age based on the average effective age of labour market exit. Ad hoc calculations are useful and often focused on interesting topics, such as career breaks and replacement ratios. They are uniform and based on common assumptions. Furthermore, they usually combine a range of assumptions, statistics and real data on individuals. Simplified example cases are one way of making cross-country and scheme level comparisons, but based on our experience with pension and working life related topics they are often unrealistic. Dynamic microsimulation is an advanced tool for analysing life courses which yields far more accurate information on the variation of indicators across individuals. If detailed longitudinal data are available, microsimulation is definitely the method of choice for analysing life course stages.

The SPC Pension Adequacy Report ((EU PAR, 2018a; EU PAR, 2018b) focuses on exploring number of measures of pension adequacy, namely poverty, income maintenance and duration of retirement (EU PAR, 2018a; EU PAR, 2018b; EU PAR, 2021). The related indicators measure the key functions of pension systems. According to the report the average duration of retirement in EU countries in 2018 was 20.8 years, down by two years from 2008. In Finland the figure was about 22 years at both points. The PAR report also has a complementary indicator: the ratio between average retirement duration and working life. In 2016 the figure for Finland was 52 per cent (EU 51 per cent). Similar indicators are also used in the OECD’s Pensions at a Glance (2019) report, where they show the remaining life expectancy at labour market exit (OECD, 2019a). Data for Finland show that in 2018, the expected remaining life expectancy (duration of retirement) for men was 19.1 years and for women 23.5 years. Macro or pension system level AWG calculations provide predictions of average contributory time, which can be considered a proxy for length of working life. A more in-depth discussion about life expectancy in sustainability framework can be found in Ayuso et al. (2020).

Established indicators of life course are either retrospective or expectation-based in nature. Employment rate and length of working life are retrospective indicators, that is, based on historical records. There are not many European countries that have national indicators for length of working life. Finland does have a retrospective indicator of working life, which shows that the average length of working life for all retirees in 2019 was 31.7 years (median 36.5 yrs.), while the figures for old-age retirees were 35.4 and 39.1 years, respectively (Pension Indicators, 2020). Similar cross-country examples are hard to come by. As for expectation-based indicators, Eurostat (2021a) provides time series (since 2000) for the expected duration of working life. The indicator gives the average number of years that a 15-year-old is expected to take part in the workforce during the remaining years of life. In 2019 the figure for Finland was 38.9 years, compared to 35.9 years for EU27 countries (Eurostat, 2020). The expected remaining lifetime since last employment is an expectation-based indicator and a proxy for the duration of retirement (OECD, 2019a).

A basic knowledge of the statutory pension system in Finland is necessary in order to understand the new indicator developed in this study. A general introduction can be found in the SSPTW-Europe (2018), Tikanmäki et al. (2019) and EU PAR (2018b). Two recent reforms of the statutory earnings-related system (in 2005 and 2017) are particularly important in terms of pension accrual and the range of benefits available (for more information on the 2005 reform, see Lassila and Valkonen, 2007 on the 2017 reform, and see Tikanmäki et al., 2015). The universal public pension system consists of the national pension and the guarantee pension. The national pension system has remained unchanged for decades in terms of the range of benefits and pensionable age (65 yrs.). The introduction of the guarantee pension in 2011 marked a significant improvement in the position of low pension earners.

Most European countries are committed to strengthen the connection between increasing life expectancy and pensionable age. This is also reflected in Finnish pension policy. The 2005 pension reform introduced the life expectancy coefficient in order to adjust pension levels according to the increase in longevity. The reform in 2017 went one step further as pensionable age was tied to the growth of life expectancy. In order for us to be able to reliably evaluate changes in life course stages it is essential that we have access to indicators that reach beyond incomes. A sensitive enough indicator should be able to verify the implied changes in the lengths of working life and retirement.

We have previously introduced a new life-cycle indicator – partition of the life course – in Tikanmäki et al. (2015) and Salonen (2020). Its purpose is to establish how large a part of their life course individuals spend in the active labour force, in retirement and in other labour market relevant stages. Using simulated data from the Finnish ELSI model, we constructed a four-state indicator of the simulated adult life course. It was initially introduced in Tikanmäki et al. (2015), where the indicator was used to demonstrate how length of employment and retirement changed as a result of the 2017 reform. The indicator confirmed modest but desirable effects of the reform, that is extension of working lives and shortening in length of retirement. The indicator was then further elaborated in Salonen (2020) to illustrate the life course stages by different levels of education and by gender.

In this study we develop the indicator further and introduce it more systematically to the microsimulation community. First, we illustrate the partition for a larger range of cohorts. Second, we show individual-level variation in the length of working life and duration of retirement by educational groups. Third, we show the partitions of retired life and working life (cf. PAR) for some recent and future retirees.

The design of our study is unique in the sense that it allows us to merge simulated data with historical records and therefore to significantly extend the study period. Our data for pensions cover the period 1980–2090 and for employment 1963–2090. With a follow-up period of well over 100 years, we can study the life courses of several sub-populations. Furthermore, as the ELSI model currently simulates the total Finnish population, our results are unaffected by small sample issues or population-related biases.

Next, we discuss some background issues, introduce our data and analytical framework and present examples of life course partition for selected cohorts and retirees. We illustrate the distributions of length of working life and retirement, and make comparisons with existing indicators. We address the potential biases of the indicator and conclude our study with a discussion.

2. Background

2.1. Microsimulation in life course analysis context

Dynamic microsimulation is a natural tool to analyse life course events and life course stages. Established dynamic microsimulation models yield information of social sustainability from micro-economic many perspectives. The natural references for microsimulation are sustainability indicators by international organizations such as OECD and EU. Microsimulation practitioners make advances in life course analysis. For example, detailed health and life situation simulation is becoming more popular (Skarda et al., 2021).

Microsimulation has already been used to supplement established calculations presented in pension adequacy reports for selected countries (Dekkers et al., 2015; Dekkers et al., 2018). Another life cycle modeling tradition focuses on indicators of actuarial fairness and present value based benefit-to-tax ratio (Moscarola, 2009). Advanced dynamic microsimulation modeling, using behavioural equations, can also be used to study broad range of pension sustainability indicators (Patxot et al., 2018).

Although there are established models, yielding valuable information, there are also some limitations. For example, household units can be problematic when counting pension of own right, which is individual benefit like most statutory pensions. Another common limitation is range of outcome years available. In many countries there are no comprehensive historical records. This limits the analysis on future life course stages.

To our knowledge similar partition indicator, which is based on true labour market measures over long time period and total population has rarely been published.

2.2. Partition approach

Simple and tractable partition approach could be useful in the aforementioned context, elaborating micro-economic sustainability indicators (e.g. lifetime contribution and benefits profiles). The precondition is that there is sophisticated simulation model and comprehensive historical data available.

We recognise that outlining this kind of analysis and using simulated outcomes with historical data will lead to many simplifications and limitations. The information contents available is limited to administrative register sources of the Finnish pension system. An effort was not taken to collect comprehensive data (social benefits or education) from other sources. This means that the partition is based on measures, which influence pension accrual and pension payment.

Regarding life course stages, there are some obvious measures, such as health and education, which have to large degree been omitted. There is a large body of research (Kontis et al., 2017; Ranabhat et al., 2018; OECD, 2019b) and microsimulation analysis ( Marois and Aktas, 2021) on the connection between life expectancy and health, which certainly indicates that health influences work ability and time spent in life course stages. According to Eurostat Finnish women are expected to face 54.8 years of healthy life, and for men the value is 57.7 years. Both numbers are below EU average (Eurostat, 2021b). The ELSI model, which we use to simulate future lives takes life-expectancy from national population forecast – similar to Eurostat – with inherent assumptions about health. Disability pension indicates negative risk on lifetime.

There is an education dynamics in the model which to some degree takes educational differences in life expectancy into account. However, the historical records lack detailed information about, for example, the duration of education, which makes the partition limited in measuring education or interleaving of work and education. A note is in order on the fact that in Finland students (after compulsory education) generally work while studying. Based on comprehensive register material it is shown that nearly 90 per cent of students in secondary education and higher level participate in paid work (Salonen et al., 2014; Saloniemi et al., 2020). The share is likely significantly lower in many other countries with different educational systems and traditions. As paid work is contributory, working life begins relatively early in Finland. Partition approach takes this fact as given, though education (or interleaving state of employment and education) could be one essential stage of the life course and part of our indicator. The problem is the previously mentioned lack of measures.

Another limitation is the measure of part-time work. This means that we cannot analyse in detail (create model state) the amount of work that is the composition of the working life. It can be argued that part-time work is inherent in our data, and the results are generalizable, but we cannot separate it.

In addition to limitations in data contents, the modeling approach of ELSI allows model transitions in one year time intervals. This initiates some challenges in measuring gradual changes such as increase in pension age or short social security spells. From administrative registers we know that the average duration of sickness and unemployment spells is one week, though they oftentimes accumulate over individual life course. ELSI model and historical records cover only long-term absence from work. Analysing the effect of pension reform with gradually increasing pension age on the length of working life is merely a rough estimate. This roughnes follows from the state modeling approach of ELSI. Gradual transitions in the labour markets are taken into account in yearly transition probabilities.

Despite limitation in measurement, partition can be useful and sensitive enough indicator to evaluate durations of working life and retirement (and their share) in the context of pension reform. The sensitivity follows from the possibility study range of (adult aged) successive cohorts.

Although there are expectation-based estimates of working life and retirement in Finland (Leinonen et al., 2018), there is value added in merging exceptionally long historical data with simulated outcomes. Partition takes advantage of all relevant measures which influence accrual time (working life) and retired time, using unique possibilities of microsimulation to simulate life expectancy.

3. Data and methods

3.1. Combining historical records with microsimulation outcomes

The data for this study are drawn from the Finnish dynamic ageing microsimulation model ELSI. The model is well documented in Salonen (2020) and Tikanmäki and Lappo (2020). In appendix A 4. there is an up-to-date description of ELSI model. In this study we use the individual-level population and labour market outcomes (model state) of the baseline simulation. The baseline simulation shows the development of employment and retirement for the adult population under current pension rules and in the light of macroeconomic projections for the period from 2009 to 2090.

The study population comprises the Finnish population and cohorts born in 1925–1990, a total of 3.8 million individuals. These are all real individuals because we chose to exclude model-generated individuals (born after 1990 and immigrants) from the study population.

In addition to ELSI outcome data, we have extended the dataset with historical records from administrative registers. These registers contain information on all pensionable employment contracts (since the 1960s) and compulsory pensions (since the 1980s). For a brief description of the Finnish pension system see ETK (2021). In practice, we have constructed roughly the same employment, retirement and population states as in the simulation period. The historical records extend many of the model states several decades backwards from 2009.

The following briefly introduces the Finnish pension rules, which have a major influence on the measures used in this study.

3.1.1. Pension rule changes affecting life course measures

The Finnish residence-based national pension system was introduced in 1955, while legislation on the contributory employee pension system entered into force in 1962. Since then, information on pensionable employment contracts and actual pensions has been systematically recorded in administrative registers. The statutory pension system is highly comprehensive, covering close to 100 per cent of the employed population. This is important to obtaining unbiased population estimates. Having said that, historical changes in pension age limits are particularly relevant to this study and the measurement of working life.

Pre-2005 pension rules included both age limits and limitations regarding pensionable wages and pension accrual. Pension accrual generally started at age 23, and during the 1960s and 1970s there were rather strict limitations regarding pensionable wages in terms of the amount of wages and duration of employment. Early retirement became a highly popular option with the introduction of several early retirement benefits in the 1980s. The major pension reform in 2005 lowered the age limit to 18 years, and a flexible retirement age was adopted. Several early retirement benefits have subsequently been discontinued. The latest reform in 2017 introduced parametric changes to current benefits. For example, the age limit for employees was lowered to 17 years. In addition, two new benefits were introduced in the form of a partial old-age pension and years-of-service pension. The partial old-age pension is a subjective benefit and has no restrictions regarding employment while receiving a pension. It has gained strong popularity in its early years (since 2017). Under current rules the major routes to retirement are disability pensions, partial old-age pension and old-age pension.

All the aforementioned – including the rule changes and the maturation of the pension system – is reflected in current pension benefits and employment contracts, and the relevant information is recorded in administrative registers so that it can be collected and merged with simulated population data. The ELSI model applies 2017 rules and simulates future life course events following the model’s parameters and assumptions.

3.1.2. Model state aggregation rules

The primary measures of the new indicator developed here are based on ELSI’s simulated labour market and population states. ELSI’s modeling states form a coherent, exclusive and non-overlapping framework of states for the adult population. In appendix A 3. there is a description of ELSI model states. The simulated states can be aggregated to obtain measures of the most essential life course stages: adolescence and compulsory education (<18 yrs.), length of working life (Employed), duration of social security benefit spells (Social security spells), working while in retirement (Employed and retired), early retired and old-age retired (Retired) and residual time (NA). There are separate and exclusive stages for early retired and old-age retired. The respective ELSI model states are shown in Table 1.

Table 1
Aggregation rules for life course stages in 1963–2090
Life course stage Rules 1963–1979 Rules 1980–2008 Contents 1963–2008 Rules 2009–2090 Contents 2009–2090
Employed Workdays > 0 Workdays > 0 Workdays based on pensionable employment contracts 1,15,16 Employed
Social security spells Pension credited benefit days > 0 Pension credited benefit days > 0orNo workdays and not drawing a pension Increment for credited periods, including long-term unemployment, sickness and parental benefits 2,3,4,13,19,20 Long-term unemployed, on sickness benefit and permanently inactive
Employed and retired NA Drawing a pension > 0 and workdays > 0 Workdays and on part-time pension or on disability pension 5,10,11 Employed and on partial disability pension or on partial old-age pension
Retired NA Drawing pension > 0 Old-age pension, disability pensions, early old-age pension, unemployment pension and farmers’ special pension 6,7,8,9,17,18,21,22 Old-age pension, disability pensions, partial old-age pension and years-of-service pension
Old-age retired NA Drawing a pension > 0 Old-age pension 8,21 Old-age pension
Early retired NA Drawing a pension > 0 Retired excl. old-age pension 6,7,9,17,18,22 Retired excl. old-age pension
<18 yrs. Adolescence (in compulsory education)
NA Not classified above

  1. Notes: Drawing a pension in one’s own right at 31 Dec. Workdays and employment cover both private and public sector employed and self-employed. Rules for 2009–2090 are based on ELSI model states, see Salonen (2020).

Roughly the same rules can be applied to create measures for time prior to simulation, that is, historical data drawn from administrative registers. However, somewhat limited information is available for constructing similar labour market and population states as in ELSI. Employment is based on working days per year. Information about social security benefits is limited, based on pension credited benefit days per year. Information about working while drawing a pension is based on yearly working days and pension (31 Dec). The exact timing of pension payment and employment cannot be determined. Both early retirement and old-age retirement can be determined accurately. To account for missing information, a ‘NA’ status is also determined, as a residual category after the aforementioned states are fixed.

As we can see from Table 1, the missing data issues locate in historical records. Using observed or true measures, imputation techniques could be used to fix the issue of missing information. We selected not to do any imputation for two reasons. One, imputing employment (prior 2008) would make pension accrual unreliable. Two, imputing pension (prior 1980) is in practice impossible because there is no baseline pension distribution from where to draw estimates. Three, it would add another dimension to partition that is already complicated by several assumptions.

Data on social security benefits are not as precise as in the simulation. During 1963–2004 a technique was applied that was known as pension credited benefit days: this measures unemployment, sickness and parental benefit spells (sum of days yearly). The spells recorded in historical registers only include days outside employment contracts. In the majority of cases the aforementioned benefits are interspersed with employment contracts (especially family benefits) and thus no completely accurate measure is available. Because of the historical benefit rules pension credited benefit days can be considered an indicator of the long-term receipt of the benefits mentioned.

The ELSI model simulates mortality so that it is aligned with the projections of population forecasts. Mortality simulation considers several factors, such as age, gender, model state, and level of education. In counting the partition, we draw mortality data from historical registers until 2008. Thereafter year of death is determined based on the assumptions applied in microsimulation.

Information about pensions is the most solid part of the partition. For the historical period (1980–2008) pension status is determined according to the situation as at 31 Dec, otherwise it is drawn from ELSI. The historical measure includes information on pension benefit and funding source (compulsory earnings-related pension or national pension). It is necessary to note that the concept of pension is defined as a pension received in one’s own right, which means that survivors’ pensions are excluded.

Level of education is simulated in ELSI. An education dynamics is at work which yields natural progression in the individual level of education during the simulation period (for more illustrations of education dynamics in ELSI, see Salonen et al. (2019)). Level of education in the historical period (1990–2008) is drawn from Statistics Finland databases. In this study the individual’s highest level of education is used as a classifier in the tables and figures. In the partition, compulsory education is based on fixed age. Any subsequent further education has no influence on population or labour market states and does not constitute a life course stage in this analysis.

3.2. Partition of the life course

Partition of the life course is a simple indicator. When the underlying data is coherent and unbiased, the calculation of life course stages is straightforward. The underlying data matrix should be complete, and each year-specific labour market and population state must be determined. There may be no overlapping states, that is, yearly states and aggregated life course stages must be exclusive. Time must be discrete, based on yearly measures. Sufficient coding of stages is obtained by adding individual yearly states over the adult life course, that is, from age 18 until death.

In practice, the aggregated model states, that is, life course stages (LCS) are binary coded {0,1}. Each LCS obtains a yearly value of one if underlying conditions are met, and assuming that the individual is alive and over 17 years of age. It is therefore possible to count sums for the whole study period t (1963–2090). The LCSs follow the classes c outlined in Table 1. The LCSs are recorded on individual level i, but it makes sense to count LCSs on a more aggregate level, that is, by some sub-group j, such as by cohort or gender. First, we get the average group-specific LCSs by

L C S - j c = 1 n ∑ t = 1963 2090 ∑ i = 1 n s i j t | L C S c .

Next, we sum exclusive LCSs to obtain an exact measure of lifetime (LT). Exact LT is simply a sum of average LCSs (Employed, Social security spells, Employed and retired, Early retired, Old-age retired and NA) and fixed length of adolescence (17 yrs.).

L T j = 17 + ∑ c = 1 6 L C S - j .

To put it simply, partition of the life course is a collection of LCSs for a certain sub-population that meets the expected LT.

4. Results

4.1. Partition of the life course for selected cohorts and retirees

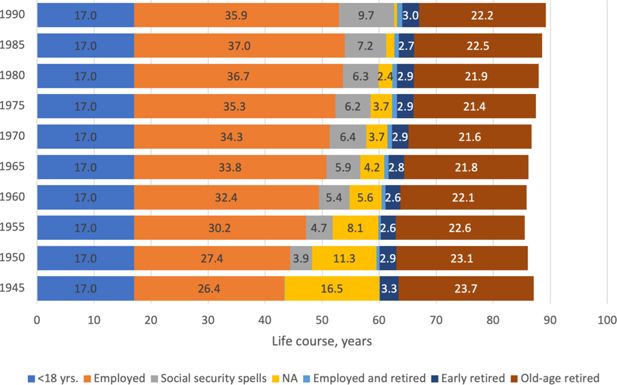
In our data it is possible to visualize the partition of the life courses for all cohorts born in 1945–1990. Figure 1 shows the partition for selected cohorts. It is clear that the measures for cohorts with a high share of historical information (i.e., those born in 1945–80) are biased. For these cohorts the measure of ‘Social security spells’ is biased mainly because of family benefits. Another source of bias is ‘NA’, which includes some periods of inactivity and employment. All this means that length of working life is not entirely accurate for the older cohorts, although for younger ones it should be. Due to the caveats related to working life, lifetime for the older cohorts is also exaggerated. Overall, working lives are increasing in length as expected. For a range of younger cohorts, the expected length of working life is 36–37 years.

Figure 1
Download asset Open asset
Partition of the life course for cohorts born in 1945–1990, years

Length of retirement, both ‘Early retired’ and ‘Old-age retired’, on the other hand, should be an accurate measure. The measure is mainly determined by empirical and simulated mortality (drawn from population records and forecasts), which are relatively easy to simulate in a dynamic microsimulation framework. It is worth noting that the youngest cohort has a maximum age of 100 years because the simulation ends in 2090. Their length of retirement is therefore slightly underestimated. However, the increase in the length of retirement is stabilizing or slightly decreasing, as it should be. According to Figure 1 the average length of old-age retirement is roughly 22 years and that of early retirement 3 years, yielding a total length of retirement of 25 years.

It is clear from the increasing dominance of ‘Social security spells’ in Figure 1 that young cohorts spent longer periods on social security. This is mainly explained by the 2005 pension reform, which expanded rights. The implementation of 2005 rules is visible in cohorts born in 1985 and 1990. The adult life courses of cohort born in 1990 are totally based on microsimulation (2008–2090), and the amount of social security spells follow assumed labour market transitions in ELSI. The social security spells over early years (prior age 23/2008) of the cohort born in 1985 are slightly shorter because of different rules. Otherwise, the cohorts face relatively similar labour market transitions.

Today, increasing numbers are working while drawing an old-age pension in Finland, a circumstance that has attracted increasing debate. However, in the partition this category (Employed and retired) has only a minor role, which is mainly explained by assumptions about the use of partial disability pension and partial old-age pension in ELSI. It is assumed that a larger share of these pensions are full pensions and therefore classified under ‘Early retired’.

A note is in order on the fact that the lengths of life course stages across cohorts are somewhat biased because of limitation in data sources, and pension rules. Long history of gradual changes in pension rules and implementation of reforms is visible in cohort specific partitions. Cohorts with major share of working life completed before 2008 face strict accrual rules, which underestimate employed time and also social security spells. On the other hand, cohorts with high share of working life completed since 2008 face relatively accurate working lives, and slightly overestimated social security spells. We can also see a relatively stable share early retirement across cohorts as well as slight increase in the share of working while drawing pension.

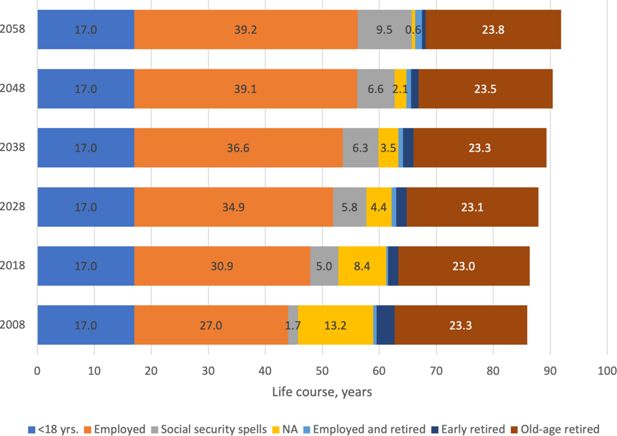
Another way of visualizing the partition is to subset the analysis of retirees over the simulation period (since 2008). 2 From Figure 2 we can see that working lives have become longer, which is also evident from the statistics. To some extent the same caveats apply cohort-wise as in Figure 1. A share of the length of working life is classified as ‘NA’ for retirees in 2008 and 2018. For future retirees we can expert working lives of 40 years.

Figure 2
Download asset Open asset
Partition of the life course for simulated retirees in 2008–2058, years

Length of old-age retirement is stabilizing at around 23 years. We also see that stricter rules for early retirement lead to shorter durations. Over the longer term, Finnish pension policy has become increasingly restrictive, phasing out several early retirement benefits and closing certain routes to retirement, particularly since the 2017 pension reform. Today, there remain essentially three possible routes to early retirement: disability pensions, partial old-age pension and long-term unemployment (the so-called unemployment pathway to retirement). ELSI aims to simulate starting pensions, taking into account how rule changes affect retirement behaviour. This is reflected in the length of ‘Early retirement’. The share of working while receiving a pension (Employed and retired) is slightly increasing.

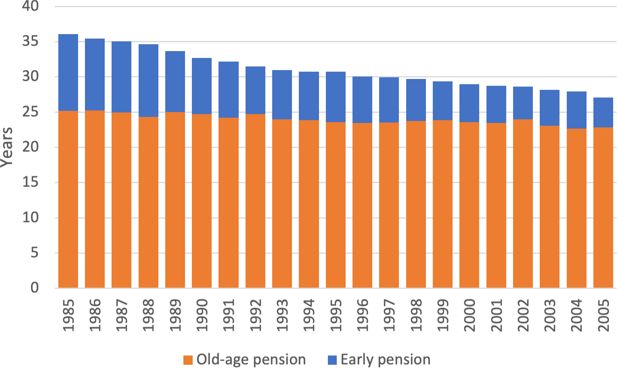
To put these numbers into perspective, Appendix A 2. shows the average length of retirement for some historical years. It is clear that early retirement was a concern in the 1980s and 1990s. On the other hand, pension rules ensured that the length of old-age retirement was under control.

The simulated data also allow us to analyse interindividual variation in life course stages. Figure 3 shows the length of working life for retired persons in 2018 by gender (M=men, W=women) and level of education. The total length was 30.9 years (cf. Figure 2), but there is a notable difference between these background factors. On average, men have longer careers than women in all educational groups; the only exception is in the category of secondary education, where men and women have careers of equal length. The difference is greatest in higher university education. Overall, this kind of analysis visualizes the great difference and variation between educational groups. Persons with a lower education have fragmentary working lives. Education is also a valid proxy for socioeconomic class, even though it is not a dimension in ELSI.

Figure 3
Download asset Open asset
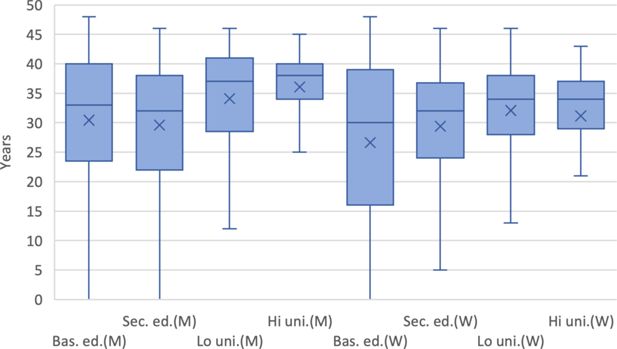
Distribution of the length of working life for retirees in 2018 by level of education and gender (M=men, W=women), years.In box and whisker plot, the box represents 50 per cent of the distribution and whisker ends 95 per cent. Line in the box is median and x is the mean.

Figure 4 illustrates the last stage of the life course. The overall length of retirement was 24.6 years, but there is notable variation especially between genders. Women’s lower mortality means they spend a significantly longer period of time in retirement than men.

Figure 4
Download asset Open asset
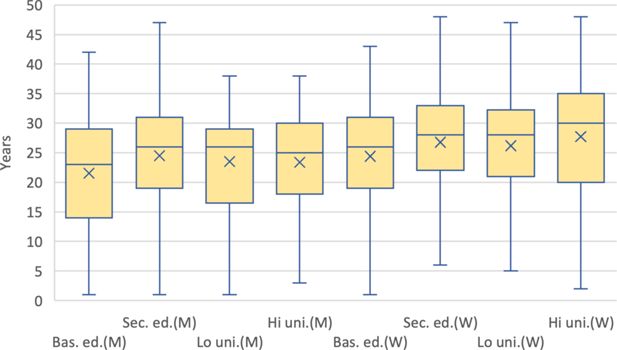
Distribution of the length of (total) retirement for retirees in 2018 by level of education and gender (M=men, W=women), years. In box and whisker plot, the box represents 50 per cent of the distribution and whisker ends 95 per cent. Line in the box is median and x is the mean.

4.1.1. Biases in life course stages

Dynamic microsimulation can of course in itself give rise to biases. The combined effects of a wide range of assumptions, measures and time must be controlled in the simulation framework. The more sophisticated the model, the greater the difficulty of controlling, for example, outcome distributions and sub-populations. However, simulation practitioners are expected to have at least reasonable control over model-based biases. At least simulation-initiated biases are well-known.

This kind of approach to merging historical records with simulated outcomes inevitably gives rise to several further biases. The key point to note here is that the initial measures are not uniform. We cannot replicate the same labour market states for the historical period as in a simulated period. ELSI has detailed states that are designed to measure life course events and states that are relevant from the point of view of current pension and accrual rules. Historical records entail pension rules and life course measures from past decades. For example, we know that there are shortcomings in measuring historical employment that lead to a fragmentary picture of working lives. In this study we made the choice to define employment state prior to 2008 based on the smallest possible duration of employment (>0 days per year). In the simulation period employment is determined separately without considering the number of working days because ELSI does not simulate days. With respect to historical employment, it is also necessary to note that accrual rules were relatively restrictive in the 1960s and 1970s. For instance, the lower age limit for pension accrual was 23 years until 2005. Based on both accrual rules and age limits it is reasonable to assume that for older cohorts, length of working life is an underestimate. On the other hand, length of retirement (time between retirement and death) can be measured reasonably accurately over the whole study period.

Another note is in order on non-uniform measures related to career brakes. Over the course of the ELSI simulation there are detailed measures for unpaid periods (social security spells), which to some degree are overestimated, as in some situations a short spell can initiate a duration of one year. Historical records provide no similar detailed information on the cause of career brakes, and prior to 2005 some social security spells are interwoven with employment. Overall, the increment for credited periods (pension credited benefit days) can be considered to underestimate the length of social security spells over the life course (until 2005).

One final note must be made regarding the target population. In analysing simulation outcomes where the total population is involved, including migration flows, it is often necessary to restrict the study population somewhat. Migration would introduce a clear bias into the proposed indicator and therefore the choice was made to focus on the native population, in other words immigrating and emigrating individuals are excluded. Migration is a fact also in Finland and it has implications on the sustainability indicators of pension system. The selection to limit the analysis on the natives only is based on limited measures about migration. From historical records, migration could be analysed only from 1990s even though it is modeled in detail in the simulation (2008–2090).

4.2. Comparisons with PAR indicators

The previous section gives rise to the question of how the partition can be compared with other indicators established indicators, that is, duration of working life and pension. Before proceeding to detailed comparisons, following generalizations can be drawn from the indicators (Table 2).

Table 2
Summary of indicators
Duration of working life
Expectation based approach
Based on a sample from microdata (LFS)
Focus on labour force participation (employed or unemployed)
Regularly updated
The expected duration of working life for retirees in 2019 is 39 years
Duration of retirement
Expectation based approach
Based on a sample from microdata (LFS)
Fixed years available, retirees in 2018
The expected duration for retirees in 2018 is 22 years
Partition of the life course
Extended microsimulation approach
Distributional measures of individual variation
Based on total population including sub-populations
Coherent individual life course stages
Focus on pension accrual
Early retirement and old-age retirement
The average duration of retirement for the retirees in 2018 is 23 (old-age retired) or 24.6 (inc. early retirement) years
The average duration of the duration of working life for the retirees in 2018 is 30.9 years

The Pension Adequacy Reports (2018 and 2021) include two indicators for the duration of pensions across Europe (28 EU countries). The first indicator is the duration of pension payment (in years) from the end of the last period of employment. 3 This measure is counted for 2008 and 2018 in order visualize change. The second indicator combines active working life and duration of retirement. This indicator illustrates the situation for retirees in 2018.

Overall, the PAR results show that in most countries, the duration of retirement is getting slightly shorter, and furthermore longer working lives are associated with shorter retirement durations. In most countries this is due to the fact that effective labour market exit ages are rising faster than life expectancy at retirement. Finnish figures for 2008 and 2018 show that the duration of retirement was about 22 years, about the same as in the EU on average.

Using the outlined partition of the life course, we have selected a collection of cohorts to make comparisons with PAR examples. Figure 5 shows that the overall average duration of retirement in 2008 was 26 years, decreasing to 24.6 years in 2018. Future retirees can expect to reach similar durations. We can also see a difference between men and women. In 2008 the average duration of retirement for women was 27.7 years and for men 24.3 years. Leinonen et al. (2018) men’s average duration decreased slightly more than women’s. There is some discrepancy between PAR indicators and the partition in the length of ‘Retired life’. It seems that the PAR figures are closer to the duration of old-age retirement.

Figure 5
Download asset Open asset
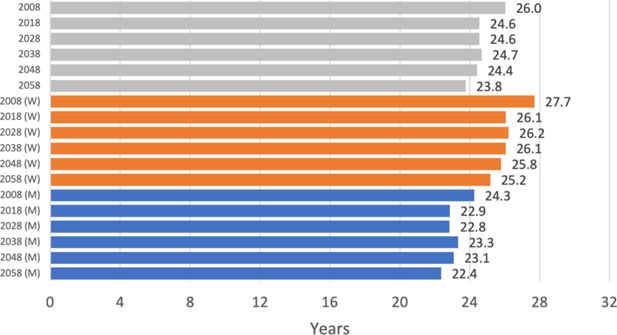
Average duration of retirement (including early retirement) by cohort and gender (M=men, W=women), years

Figure 6 shows the duration of both working life and old-age retirement. These come closer to the PAR figures. For retirees in 2018, the partition indicates an average working life of 30.9 years and a retirement duration (Retired life) of 23 years. With the extension of working lives, future retirees will have similar lengths of retirement. This comparison shows that the working lives implied by the partition are underestimates compared to the PAR indicator. 4 . The survey and expectation-based figures of the Ageing Europe report indicate a duration of 39 years for retirees in 2019.

Figure 6
Download asset Open asset
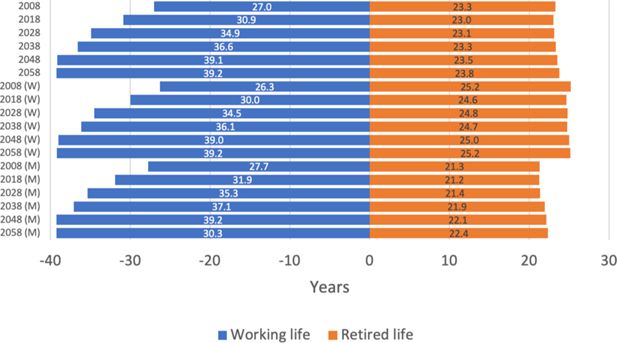
Average duration of retirement (old-age pension) and duration of working life by cohort and gender (M=men, W=women), years

As the partition of the life course can be presented for sub-populations, we can study the retirees in 2018 in more detail. As we can see from Figure 6, women have initially shorter careers until the difference between men and women stabilizes. On the other hand, women have consistently longer retired lives.

Another established indicator at a more aggregate level is the ratio of retired life to working life. Table 3 shows the distribution of this ratio measured individually. For recent retirees (2018) the ratio averages 1.08, which means that retired lives are longer than working lives. This underlines a critical issue for the sustainability of the pension system. In a financially sustainable pension system, people should work longer. Working lives – in essence contributory time – should be longer than the duration of pension payment. However, as the analyses above indicated, the trend is towards longer careers and more shoter retired lives.

Table 3
Distribution of the ratio (length of (total) retirement/length of working life) for retirees in 2008–2058
Year P10% P25% P50% Mean P75% P90%
2008 0.40 0.64 0.93 1.38 1.35 2.33
2018 0.31 0.55 0.78 1.08 1.06 1.65
2028 0.31 0.51 0.70 0.88 0.91 1.33
2038 0.33 0.51 0.67 0.80 0.86 1.19
2048 0.34 0.49 0.63 0.69 0.78 1.00
2058 0.35 0.49 0.61 0.65 0.76 0.91

5. Discussion

This kind of extended analysis of individual life courses is illuminating because it visualizes the central stages of the life course. Generally speaking, the outcomes of dynamic microsimulation allow for the partition of life courses into economically meaningful stages. In ELSI it is possible to measure life course stages in detail, that is, both working life, retired life, social security spells and intervening stages. This kind of framework that makes use of dynamic microsimulation outcomes makes it simple and straightforward to study specific groups (e.g., retired persons or cohorts).

Although, partition yields valuable information about distributional effects, for example, of pension reform, it is also limited. Financial sustainability is beyond this analysis mainly because euros (wages, pensions and social security benefits) are not readily available.

Results show that working lives in Finland are gradually getting longer and retired lives shorter. Generous early retirement benefits have given way to a new set of stricter rules which limit the length of time people can spend on early retirement, and this is visible in the indicator. The length of time spent in old-age retirement is also getting shorter: the partition indicates that the projected length of old-age retirement is currently 22 years. Further analysis revealed some differences in the lengths of life course stages between educational groups and gender. But more notably, the distributional features across sub-populations (e.g. cohorts and retirees) are underlined by this kind of analysis covering the total population.

The partition is weakened by some issues. Most importantly data sources allow no further possibilities to consider other meaningful life course stages, such as, duration of education or parental leaves. We know that the use of parental benefits has greatly increased over study-period (since 1980s). In Finland mothers use over 90 per cent of parental benefits, which makes comparisons between genders biased. Another issue is related to inconsistencies of longitudinal measures. Short social security spells are either largely missing (1963–2007) or overestimated (2008–2090). This bias can be seen from the lengths of ‘Social security spells’ across cohorts. Despite caveats, partition can be useful in focusing attention to the ratio of the lengths of retirement and working life.

The indicator developed in this paper can be used to make comparisons with established indicators, such as working life and retired life in the Pension Adequacy Report. Partition of the life course yields similar results to PAR as regards the length of old-age retirement. The timing of retirement and lifetime are of course easy to measure in both statistics and simulation, and therefore the results are bound to be well aligned. On the other hand, the measurement of working life is subject to various biases and different concepts. Microsimulation offers the benefit of visualizing individual variance in the indicator.

Our indicator also allows for comparisons with another regular EU report (EU AWG, 2021). The AWG report’s focus is on the macroeconomic sustainability and finances of European pension schemes, and length of working life is not a major indicator. Among its numerous assumptions, the AWG calculation includes an estimate of new retirees’ average contributory period. In fact, contributory time is the key measure in defining aggregate indicators such as pensions. Assumptions about the duration of working life are a typical situation where two different analytical frameworks (microsimulation vs. macro model) could complement each other. The biases of the partition were discussed above, but the established AWG framework would certainly benefit from using microsimulation results to validate its assumptions, as outlined in Dekkers et al. (2015).

In many European countries pension benefits continue to accrue during social security spells and unpaid periods. Our analysis shows that in the Finnish context, unpaid periods account for an increasing portion of the life course. At this juncture a note is in order on the range of life course stages that can be covered using our indicator. Our analysis is limited in depicting true life course phenomena, such as time spent in education or on some universal or means-tested social security benefits. These spells are interspersed with other stages of the partition, mainly social security spells (Social security spells), employment and not specified (NA). For this reason, it is important to recognize that the proposed partition of the life course does not measure all sociologically relevant stages of the life course. However, other stages could easily be incorporated into the partition if the necessary material were available.

We also found that merging historical records with simulation outcomes introduces some bias into the partition of the life course. There is a rather limited range of cohorts for whom the measures are relatively unbiased. However, if complemented with subjective evaluation and expert opinion, this approach could be used to analyse the key pension system indicators – length of working life and especially length of retirement – for a substantial number of cohorts.

The partition of the life course should prompt discussion among decision-makers about the relative length of the active and passive stages of the life course and about differences between men and women and across social classes. The ongoing political discussion in Finland around the length of working life and pension age has mainly been limited into the context of pension reforms. By this analysis we can confirm that working lives in Finland are gradually getting longer and retired lives shorter, as expected. In the aftermath of reform new statistics have been complied about length of retrospective working life of the retirees (Pension Indicators). Eurostat publishes similar statistics for other countries. The partition gives a more in-depth view to life course stages, which can already be seen from the statistics. These results also align with the scientific debate on lifespan, namely will the strong growth in mandatory retirement age be politically sustainable when the time for implementation approaches. Length of pension on the other hand has mainly been discussed in the pension industry. For obvious reasons actuaries everywhere are concerned about the financial sustainability of the statutory pension systems. With partition it is possible to visualize distributional difference in the length of retirement across sub-groups of interest.

As a practical note, Finland has a system in place to inform citizens about the length of their working life, known as the pension record (see Työeläke.fi). It details their years of employment, the amount of earnings-related pension accrued to date (euros/month) and yearly pensionable earnings. A letter is mailed to private and public sector employees once every three years in which they are informed about their current pension status. Pension record could be considered an up-to-date proxy for length of working life. The letter certainly serves as a positive incentive towards longer working lives and better pension security.

The outlined partition can be developed and validated further. Possibilities for further research locate in target population, assumptions about what triggers a state and possible benefits from imputing missing information. A more thorough analysis of financial sustainability would require taking immigration into consideration. This is to some extent possible. The sensitivity of how many working days (per year) trigger employment state is another topic for further research. Current aim of the partition is to cover pensionable earnings and benefits. In that respect the partition is accurate. However, taking broader perspective on life courses, prompts question of should missing or biased measures be imputed to get more generalizable description of life course stages.

We conclude that merging historical records with simulated outcomes and counting a partition of the life course contribute to dynamic microsimulation. Similar historical datasets and model outcomes (states) are available in other countries as well, where microsimulation practitioners might want to contribute more to this line of research.

Footnotes

1.

The Pension Adequacy Report (2021) provides information of current and future pensionable ages (p. 56) across Europe.

2.

The number of simulated retirees are in the Appendix A 1.

3.

In practice the duration (of retirement) begins at leaving the last employment, for people who were employed at the age of 50.

4.

For other studies reporting on the duration of working life, see OECD 2019a, p. 181 and Eurostat’s Ageing Europe report 2019, p. 87.

A 1: Number of retirees

Year of retirement Count
2008 62,918
2018 65,249
2028 63,078
2038 51,821
2048 49,471
2058 35,622

A 2: Length of retirement

A 3: Population states in the ELSI model

State Description
Primarily employed (“active”)
15 Primarily employed for the first consecutive year
16 Primarily employed for the second consecutive year
1 Primarily employed for at least the third consecutive year
Sickness allowance preceding full disability pension
4 Sickness allowance preceding full disability pension
Unemployed
3 On the unemployment pathway to retirement
2 Unemployed (excluding those on the unemployment pathway to retirement)
Retired
8 Old-age pension
11 Partial old-age pension and employed
7 Partial old-age pension and not employed
17 Full disability pension for the first consecutive year
9 Full disability pension for at least the second consecutive year
10 Partial disability pension and employed
18 Partial disability pension and not employed
5 Part-time pension
6 Years-of-service pension
21 National old-age pension only
22 National disability pension only
Outside the labor force for other reasons
19 Permanently outside the labor force but has accrued earnings-related pension
13 Outside the labor force but has accrued earnings-related pension
20 Outside the labor force and has not accrued earnings-related pension
Deceased
12 Deceased

A 4: ELSI model

ELSI is a dynamic microsimulation model in the sense of time dynamics. It simulates the life course of each individual separately. Unlike many other models, ELSI does not use behavioural equations in determining model transitions. Instead, transitions between population states are based on Markovian type transition probabilities. The model has a cross-sectional aging process (one-year time steps), which builds a synthetic life history for each simulated individual. The model has modular structure. The essential part for this analysis is the first module, that is, the population module. The other modules are described in detail in Tikanmäki and Lappo (2020) The ELSI model is compared with other European pension microsimulation models in Dekkers and Van den Bosch, 2016.

ELSI is connected via a micro-macro link to the semi-aggregated Long-Term Projection Model (LTP) also developed and operated by the Finnish Centre for Pensions (see Tikanmäki et al., 2019).

The target population of ELSI comprises the entire adult population of Finland and those adults living abroad who have previously accrued earnings-related pension under the Finnish pension system. The data used in creating the source datasets is generally of high quality and comprises all people covered by the Finnish earnings-related pension system.

Population modeling in ELSI is based on 21 population states. The population state of an individual depicts their main type of activity during a given year. A person is in a single population state for one year at a time.

Within the model, population states are referred to with number codes, as shown in A 3.

There are 11 population states for retired people, mostly corresponding to the various types of pensions that a person can receive. In the case of partial old-age pension (states 11 and 7) and partial disability pension (states 10 and 18), there are two population states for both, corresponding to whether or not the person is working while drawing a pension. This makes it easier to simulate earnings for these people. Those receiving a full disability pension for the first consecutive year also get their own population state 17, as these people are more likely to transition out of full disability pension than those who have been receiving it for longer.

Those who are not retired and who are employed are divided into three population states based on length of consecutive employment. People who are employed for the first or second consecutive year are placed in states 15 and 16, respectively. Those who have been consecutively employed for longer are placed in state 1. This division makes the modeling more realistic, since it is more likely for a person to transition out of employment in the first years of being employed. States 15, 16 and 1 are also called “active” states.

People receiving unemployment benefits are also divided into two states based on whether they are on the unemployment pathway to retirement. This is because persons on this pathway (in state 3) are less likely to return to employment.

Before a person can retire on a full disability pension, they have had to receive sickness allowance for the maximum period of about one year. For this reason, we have included a separate state 4 for these allowance recipients. People who receive a sickness allowance that does not lead to full disability pension are not included in this state.

People who are outside the labour force for other reasons are in one of three states. State 20 is for those people who have accrued no earnings-related pension; these are mostly young people and recent immigrants. Those who have previously accrued earnings-related pension are either in state 13 or 19. The regular inactive state 13 is meant to be relatively temporary. In contrast, people in state 19 are much less likely to transition to other population states.

The reason for having three states for people outside the labour force is to make the modeling more realistic: there are many different reasons for being outside the labour force. Some of them tend to last only a brief period, while others are more permanent. The three states include, for example, non-employed students, those doing mandatory military service, those on child home care allowance or on a longer sickness allowance (that does not directly lead to full disability pension) and socially excluded people.

The population module is the first simulation module in the ELSI model. It simulates the development of the target population by generating new cohorts that enter the population and by modeling immigration, emigration, educational dynamics and transitions between population states. State transitions include, for example, labour market dynamics, transitions into retirement and deaths. The first simulated year is 2013, and simulation is generally done until 2085.

Population state transitions are modeled with the help of the 21 population states described earlier. With some exceptions, population state modeling has a simple Markovian structure, where the only factors affecting the probabilities of transitioning into other states are country of residence, sex, age, education level (for residents of Finland) and current population state.

There are two transitions that are modeled with longer transition paths within the Markovian framework. The population state of fully employed people has been divided into three states to better model the higher unemployment risk of newly employed people; the only way to get to population state 1 is to move from 15 to 16 to 1. A similar arrangement exists with full disability pension. The only way to transition to population state 9 is to go through state 17. This makes the modeling more realistic as the first year on disability pension holds a significantly higher probability of both rehabilitation and death. In most cases, people must also go through state 4 to get to 17. This helps to model the fact that it is usually necessary to receive sickness allowance for about one year before gaining eligibility to a full disability pension.

There are couple of minor exceptions to the Markovian structure. Probability of remaining employed is higher for those whose working life covers at least 75 per cent of their adult life. The opposite is true for people who do not meet this condition in order to keep the aggregate transition probabilities equal to those given by the corresponding transition probability matrix. Another exception is that only those people who meet the length of working life requirement for a years-of-service pension are given the chance of transitioning to the years-of-service pension state 6.

The following paragraphs detail the steps that take place as the population module simulates a single year.

The basis for the yearly simulation is, naturally, last year’s simulated data (or actual data in the case of the first simulation year). Population state transitions and immigration and emigration are modeled to occur in the middle of the year, so at the beginning we are operating with last year’s population in last year’s population states. For people in population states where everyone is employed (states 15, 16, 1, 10, 5 and 11), the length of working life is advanced by 0.5 years to account for the first 6 months of the year. People in other than these states can also have employment spells, but they are modeled later in the earnings module. Also, people in employed states can have short periods of unemployment or other inactivity that are similarly modeled later in the earnings module.

In general, the ELSI transition probability matrix is updated by multiplying the previous year’s probabilities in such a way that they would match the corresponding LTP probabilities (alignment) if ELSI population states were aggregated to match LTP population states. In situations where a single LTP population state covers multiple ELSI states, a common multiplier is used for all states. For example, the LTP model only has a single state for primarily employed people. If in ELSI we needed for some age and sex group to decrease the probability of transitioning from primary employment to old-age pension by 10 per cent (to match the LTP model), we would multiply transition probabilities from each of the states 15, 16 and 1 to 8 by 0.9.

Different transition probabilities for different educational levels are created in such a way that on the aggregate level, weighted by the number of people at different educational levels, they equal the corresponding LTP probability. The ratios between transition probabilities for different educational levels are generally based on the transition probability matrix estimated from the source data. To give an example, say that in the source data 35-year-old women in state 1 with lower tertiary education have a 40 per cent higher probability of transitioning into state 4 than those with upper tertiary education. This ratio will be fixed during the entire simulation period, as the aggregate probability of transitioning from state 1 to state 4 for 35-year-old women is adjusted to match that of the LTP model. A note is in order on the fact that ELSI does not simulate in detail the duration of post-compulsory education, only degrees completed.

There is a special update procedure for the main labor market dynamics, that is, transitions between primarily employed states 15, 16 and 1, the inactive state 13, the unemployment state 2 and the residual state 20. These are updated in such a way that the ratios of primarily employed and unemployed people to the population roughly match the numbers in the LTP model.

As retirement ages rise, it is necessary to simulate some transitions at ages where they have not previously been possible. When updating transition probabilities in these cases, the way in which educational level affects the probability of transition is taken from the age (or a range of ages) where the corresponding transition was last possible in the source data. For example, as the retirement age rises, it is possible to become unemployed (transition into state 2) at older ages. The way in which educational level affects the probability of becoming unemployed at these ages is taken from the probabilities of transitioning into unemployment at age 62, as calculated from the source data.

References

  1. 1
    Getting life expectancy estimates right for pension policy: period versus cohort approach
    1. M Ayuso
    2. JM Bravo
    3. R Holzmann
    (2020)
    Journal of Pension Economics and Finance 20 :212–231.
    https://doi.org/10.1017/S1474747220000050
  2. 2
  3. 3
  4. 4
    Applications of Microsimulation Modelling
    1. G Dekkers
    2. K Van den Bosch
    (2016)
    Prospective microsimulation of pensions in European Member States, Applications of Microsimulation Modelling.
  5. 5
  6. 6
    The 2018 Ageing Report: Economic and Budgetary Projections for the EU Member States (2016–2070)
    1. EU AWG
    (2018)
    EU Commission Institutional Paper 079 1.
    https://doi.org/10.2765/615631
  7. 7
  8. 8
  9. 9
  10. 10
  11. 11
    Pension Adequacy Report: Current and Future Income Adequacy in Old Age in the EU, Publications Office, 10.2767/013455
    1. EU PAR
    (2021)
    Pension Adequacy Report: Current and Future Income Adequacy in Old Age in the EU, Publications Office, 10.2767/013455.
  12. 12
    Green Paper on Ageing. Fostering Solidarity and Responsibility between Generations.
    1. European Commission
    (2021)
    Green Paper on Ageing. Fostering Solidarity and Responsibility between Generations., https://op.europa.eu/s/vREQ.
  13. 13
    Eurostat Statistical Books
    1. Eurostat
    (2020)
    Ageing Europe – Looking at the lives of older people in the EU – 2020 edition, Eurostat Statistical Books, 10.2785/628105.
  14. 14
  15. 15
  16. 16
  17. 17
    The Finnish Pension Reform of 2005
    1. J Lassila
    2. T Valkonen
    (2007)
    The Geneva Papers on Risk and Insurance - Issues and Practice 32 :75–94.
    https://doi.org/10.1057/palgrave.gpp.2510108
  18. 18
    Working Life and Retirement Expectancies at Age 50 by Social Class: Period and Cohort Trends and Projections for Finland
    1. T Leinonen
    2. P Martikainen
    3. M Myrskylä
    (2018)
    The Journals of Gerontology. Series B, Psychological Sciences and Social Sciences 73 :302–313.
    https://doi.org/10.1093/geronb/gbv104
  19. 19
    Projecting health-ageing trajectories in Europe using a dynamic microsimulation model
    1. G Marois
    2. A Aktas
    (2021)
    Scientific Reports 11 :1785.
    https://doi.org/10.1038/s41598-021-81092-z
  20. 20
  21. 21
    Pensions at a Glance 2019: OECD and G20 Indicators
    1. OECD
    (2019)
    Pensions at a Glance 2019, Pensions at a Glance 2019: OECD and G20 Indicators, Paris, OECD Publishing, 10.1787/b6d3dcfc-en.
  22. 22
    Finland: Country Health Profile 2019, State of Health in the EU
    1. OECD
    (2019b)
    Brussels: OECD Publishing, Paris/European Observatory on Health Systems and Policies.
    https://doi.org/10.1787/20656739-en
  23. 23
  24. 24
  25. 25
  26. 26
  27. 27
    Using Trajectory Analysis to Test and Illustrate Microsimulation Outcomes
    1. J Salonen
    2. H Tikanmäki
    3. T Nummi
    (2019)
    International Journal of Microsimulation 12:3–17.
    https://doi.org/10.34196/IJM.00198
  28. 28
  29. 29
    The diversity of transitions during early adulthood in the Finnish labour market
    1. A Saloniemi
    2. J Salonen
    3. T Nummi
    4. P Virtanen
    (2020)
    Journal of Youth Studies 24 :851–870.
    https://doi.org/10.1080/13676261.2020.1776229
  30. 30
    LifeSim: A Lifecourse Dynamic Microsimulation Model of the Millennium Birth Cohort in England
    1. I Skarda
    2. M Asaria
    3. R Cookson
    (2021)
    International Journal of Microsimulation 14 :2–42.
    https://doi.org/10.34196/IJM.00228
  31. 31
    Social Security Programs Throughout the World: Europe, 2018. No. 13–11801, Social Security Administration (USA)
    1. SSPTW-Europe
    (2018)
    Social Security Programs Throughout the World: Europe, 2018. No. 13–11801, Social Security Administration (USA).
  32. 32
  33. 33
  34. 34
    Distributional Effects of the Forthcoming Finnish Pension Reform – a Dynamic Microsimulation Approach
    1. H Tikanmäki
    2. H Sihvonen
    3. J Salonen
    (2015)
    International Journal of Microsimulation 8:75–98.
    https://doi.org/10.34196/IJM.00122

Article and author information

Author details

  1. Janne Salonen

    Keva, Helsinki, Finland
    For correspondence
    janne.salonen@keva.fi
    Competing interests
    No competing interests reported.
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0002-0595-6226

  2. Heikki Tikanmäki

    Finnish Centre for Pensions, Helsinki, Finland
    Competing interests
    No competing interests reported.

  3. Sampo Lappo

    Finnish Centre for Pensions, Helsinki, Finland
    Competing interests
    No competing interests reported.

Funding

No specific funding for this article is reported.

Acknowledgements

We would also like to thank the two anonymous reviewers for detailed and constructive comments on our original submission to the International Journal of Microsimulation.

Publication history

  1. Version of Record published: December 31, 2021 (version 1)

Copyright

© 2021, Salonen et al.

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Download citations (links to download the citations from this article in formats compatible with various reference manager tools)

Open citations (links to open the citations from this article in various online reference manager services)

Categories and tags