A Microsimulation Model for the Land Rental Market in Irish Farming

Cite this article as: J. Loughrey, T. Hennessy; 2022; A Microsimulation Model for the Land Rental Market in Irish Farming; International Journal of Microsimulation; 15(2); 77-101. doi: 10.34196/ijm.00264

Article
Figures and data
Jump to

Abstract

In this paper, we utilize Teagasc National Farm survey data to analyse the agricultural land rental market in Ireland with a newly developed agent-based microsimulation (ABM) model and a classical walrasian equilibrium model of the land rental market. We conclude that the microsimulation model has a number of strengths in addressing the interactions between landowners and tenants and dealing with the impact of economic changes on the farm size concentration. The equilibrium model retains some value in dealing with the question of price determination and in illustrating the potential surpluses to be gained from a more active land rental market. The paper contains a comparison of simulation results from the ABM model with recent farm-level data and Census of Agriculture data. These comparisons indicate the relevance of some findings from the simulation model including the rise in average dairy farm size and the decline in area allocated to non-dairy cattle farming. However, the sheep farming system appears to have defied the predictions from the simulation model and this may be attributed to the recent improvement in economic performance for this sector. The ABM model can be further refined to account for decisions in relation to the choice of farming system, the question of retirement and farm exit.

1. Introduction

Kennedy (1991) wrote that ‘the bulk of land transfers, now as in past times, involve kin, taking place outside the orbit of the market’. This pattern of agricultural land transfer remains largely evident in Ireland as land inheritance continues to account for the main source of agricultural land mobility (Duesberg et al., 2017; Leonard et al., 2017). Agricultural land-use decisions remain strongly influenced by motives not directly related to the profits from agriculture (Howley et al., 2015; Bradfield et al., 2020). However, there is growing evidence of an increase in profit maximization behaviour through greater activity in the medium and long-term leasing of farmland from about 2015 onwards (Revenue, 2021). A continuation of this trend could significantly reduce the role of land inheritance in agricultural land mobility.

In addition, recent evidence points to an increase in the average size of dairy and tillage farms with small reductions on non-dairy cattle farms, the latter comprising the majority of farm holdings in Ireland (CSO, 2022). A continuation of this increase in dairy farm size may have important implications for structural change in Irish agriculture, farm size concentration and environmental pressures. Recent research concludes that the participation in agricultural land rental markets is associated with higher profitability among dairy farms in Ireland (Bradfield et al., 2020). A more active land rental market may therefore have some implications for farm profitability and the size distribution of farms in Ireland.

We analyse this expansion of the agricultural land rental market in Ireland with a newly developed Agent-Based Micro-Simulation model (ABM). In our ABM model, we attempt to address the question of how a continued increase in profit maximization behaviour could affect the farm size distribution and overall structural change in Irish agriculture via an increase in land rental activity.

Microsimulation modelling is increasingly applied to agricultural economics (Ramilan et al., 2011; O’Donoghue, 2013 and Loughrey et al., 2016). ABM models are often used to address the topic of structural change in agriculture (Reidsma et al., 2018) and broader questions relating agriculture with the environment (Schulze et al., 2017). Berger and Troost (2014) explore ABM models in agriculture and emphasise the importance of accounting for farm-level technical and financial constraints and the farm management and agronomic conditions of the farm. ABM models have been used to develop simulated agricultural land market auctions (Balmann, 1997, Happe et al. (2006) and Arsenault et al., 1997). Our research can therefore draw on some of the methods, which have been applied in previous models.

ABM models can account for “the emergence of structures at the macro or societal level from individual action” (Gilbert, 2007). In the context of local land markets, the entry of non-agricultural buyers into a local land market can influence the decision-making of other local farms with broader implications for the local economy and society (e.g., Brady et al., 2012). More recently, Curtiss et al. (2021) used transaction-level sales data to study farmland sales markets in the Czech Republic where an increasing influence of global Non-Agricultural Buyers (NAB) is evident. The authors find that relatively small farms did not participate in price competition with NABs and acquired land only when offered for less than the highest prices in local markets. In contrast, the relatively large farms in local land markets appeared to effectively compete with NABs.

In parallel to the ABM model, we operate a standard equilibrium model based largely on the methods outlined in (Hennessy et al., 2009). Kremmydas et al. (2018) contrasts this ‘traditional’ farm level equilibrium model with the ABM type model where market outcomes are simulated by means of individual transactions that are not necessarily determined by the forces of aggregate supply and aggregate demand. We seek to illustrate the strengths of both the ABM model and the traditional equilibrium model in supporting a better understanding about land rental markets in Ireland.

The ABM modelling approach can provide flexibility around the determination of prices where there is bilateral trading between landowners and tenants. Relative to the traditional equilibrium model, the results of the ABM model may provide a more realistic picture about the variability of land rental prices between parcels of similar quality and location. One of the main strengths of the ABM modelling approach is that the model can be used to track the evolution of the farm size distribution. The farm equilibrium modelling approach can perform well in visually illustrating the potential gains from trading in the agricultural land rental market. The equilibrium modelling approach is however, limited by the assumption of one single market clearing price and is unsuitable for analysing the influence of economic and policy changes on the farm size distribution.

The results from our ABM model show that an increase in profit maximisation behaviour could lead to a substantial transfer of agricultural land from the cattle and sheep sectors and towards the more profitable dairy sector. This is an important finding given that the environmental output of dairy farms tends to be much greater than for cattle and sheep farms. Buckley and Donnellan (2021) show that average greenhouse gas emissions per hectare from dairy farming are approximately two-thirds higher relative to cattle farms and approximately double the emissions per hectare of sheep farms. At the same time, it is recognised that economic viability is achieved by a much greater proportion of dairy farms relative to cattle and sheep farms (Ryan et al., 2016; Loughrey et al., 2022).

In this model, we show that when agricultural land is transferred solely on the basis of profit maximization, the farm size concentration can increase significantly. The farm size concentration is considered in this research given the important link between farm size and the amount of farm subsidies received by individual farms. At an EU level, this is particularly important given the shift from product-based subsidies to land-based subsidies (van der Ploeg et al., 2015). In addition, we are interested in the redistributive capacity of land rental markets and the role of such markets in assisting small farms in expanding without the need to purchase land.

We follow this introduction with an outline of some of the literature relating to the spatial dimension of agricultural land markets and the simulation of farmland auctions. In section 3, we describe the details and methods. This is followed with results and finally by the conclusion.

2. Literature

There is a growing economic literature on the spatial dimension of agricultural land markets (including simulation modelling). In the following, we describe some of the relevant economic literature including the literature concerned with simulation modelling of agricultural land markets.

Patton and McErlean (2003) identify spatial autocorrelation in the agricultural land market in Northern Ireland and conclude that agricultural land prices are not solely determined ‘by the inherent characteristics of the land, but tend to reflect also the average local price per acre’. This lagged spatial dependence is attributed to ‘the circularity of price setting’ whereby ‘property owners, prospective buyers, real estate agencies, tax assessors and others base their estimates of values of agricultural land on observed sales in the vicinity’. The spatial dimension can also play an important role in influencing the extent to which farm subsidies influence land market prices. For instance, Graubner (2018) provides a formal analysis of spatial competition in agricultural land rental markets and concludes that the land subsidy is only fully transferred to land rental prices where the importance of space is low or non-existent.

In developing a simulation model of the land market in Chile, Berger (2001) highlights the typically local nature of supply and demand for agricultural land and the importance of competition between neighbours in shaping the agricultural land market. Berger (2001) concludes that ‘in rural areas, where many farms with a high marginal productivity attempt to expand their acreage, this can lead to excessive land prices that may even prevent the realisation of economies of scale. Ignoring these spatial dynamics by assuming perfect land allocation among farms is not always an adequate representation of reality’. Storm et al. (2015) explain the advantage of agent-based models in recognizing ‘the importance of land immobility, the location of farms in space, and the interdependence of farms via competition on the spatial land market’.

Agent-based models of land markets are quite commonly applied to both rural and urban settings. For instance, Filatova et al. (2009) outline a model of the urban land market where the ‘centralized equilibrium price determination mechanism’ is replaced by ‘decentralized bilateral agent trading dispersed in time and space’. 69 makes a similar distinction between the traditional equilibrium model and the ABM model in terms of market outcomes. This modelling of ‘bilateral agent trading’ is evident in the farmland simulation models of Balmann (1997) and Arsenault et al. (1997). In practical terms, the negotiated price is unlikely to be completely detached from the levels of supply and demand in the local land market or the profitability of farming the particular land parcel. Polhill et al. (2008) therefore outline a neat method for the negotiation of selling price based on the weighted sum of the farm profitability of the purchaser, the profitability of the land parcel for sale and an exogenous interest rate.

A number of land simulation models have included the role of market power in price determination including Arsenault et al. (1997) and Filatova et al. (2009). In these models, the relative market power of buyers and sellers is attributed to the number of agents in either category. A similar approach was applied in the econometric models outlined in Cotteleer et al. (2008). Balmann et al. (2021) outline some challenges in assessing and quantifying market power in agricultural land markets including the challenges related to defining the size of the regional market. Appel and Balmann (2022) use the AgriPoliS and FarmAgriPoliS models to explore how very fast-growing farms in Germany may affect their neighbours with results indicating ‘that large, fast-growing farms with high profitability and a higher maximisation tendency have negative effects on the sizes and profitability of other farms in their neighbourhood’ with implications for higher land rental prices.

Elsewhere, Freeman et al. (2009) accounted for the impact of farm income variability and risk aversion in influencing the bidding price. Some land market simulation models are based on one period of time where the focus is placed on the static impact of policy changes e.g. Viaggi et al. (2013). A number of other models have a multi-period setting including Balmann (1997) and Bert et al. (2015).

Details and Methods

Grimm et al. (2006) provide a comprehensive protocol to guide the development and published description of ABM models known as the ‘ODD’ protocol and has the primary objective of making model descriptions more understandable and complete. Grimm et al. (2010) conclude that the ODD protocol improves the rigorous formulation of models and helps make the theoretical foundations of large models more visible. Under the ODD protocol, there are three blocks 1) Overview 2) Design concepts and 3) Details.

The Overview block contains three elements 1) Purpose 2) Variables and Scales 3) Process Overview and Scheduling.

Purpose

Our ABM model is applied to explore the impact of a change in land-use decision-making at the farm level on overall farm structures and the farm size distribution. We seek to demonstrate the potential contribution of the ABM model to the understanding of agricultural land rental markets and in describing the determination and distribution of land rental prices.

Variables and Scales

Our ABM model is based on Teagasc National Farm survey data, which forms the Irish component of the FADN database. We describe the dataset and the variables in more detail in the input data section. The farm business is the unit of analysis. The level of spatial detail is based on NUTS 2 and NUTS 3 regions. This low level of spatial detail is due to the relatively small sample size. The regional location, the soil quality and the farm profitability are among the key low-level state variables included in the model. Aggregated variables include the following: the share of the agricultural area being rented in each region and the degree of farm size concentration or inequality in each region. Ideally, we would avail of more spatially disaggregated data on the distribution of farmland and tenure. However, this data is not available at the farm-level.

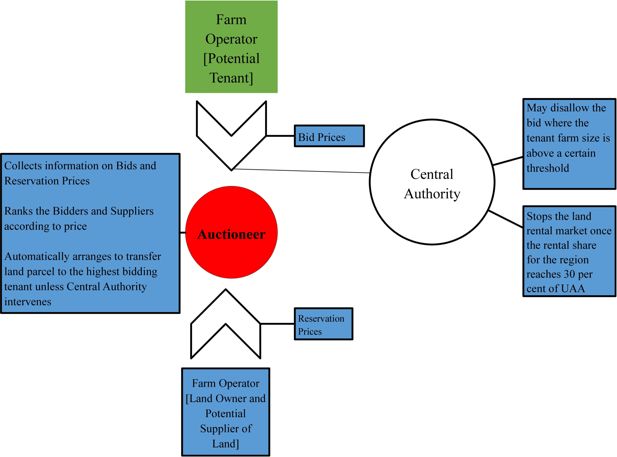
Figure 1 describes the main participants in the land rental market and their relationship under the ABM model. Firstly, the farmer population in each region is divided into two main segments 1) a group of farm operators that will potentially make a bid for acquiring additional rented land 2) a group of farm operators who are willing to let out some of their farmland in return for rental payments. In the ABM model, a fictitious market agent or auctioneer mediates between these two groups of farmers. The first group contains some farmers who are initially participating in agricultural land markets and some farmers who may not be participating initially in agricultural land rental markets. A list of model assumptions is included in Table A2 in the Appendix.

Figure 1

Download asset Open asset

Description of the Agent-Based Model of the Agricultural Land Market

Process Overview and Scheduling

In the ABM model, the activity in the land rental market takes place sequentially in contrast with the instantaneous adjustment that can be assumed in equilibrium models. The auctioneer collects information from both farmer groups about their willingness to participate in the land rental market i.e. their willingness to pay or accept money in exchange for renting a particular land parcel. Land parcels are released to the market in sequence and beginning with the land parcel with the lowest willingness to accept. The willingness to accept is determined by the landowner based on their farm profitability and the prevailing market prices for agricultural land in the region.

In this model, the market operates through sealed bids with each market participant from the first group (potential tenant farmers) making a maximum of one bid per available land parcel. For each available parcel, the bidder with the highest bid gains access to the land through a rental agreement with the landowner. It is assumed that the landowner makes decisions with reference to a reservation price, below which the landowner will not release land to the market. Those landowners who are willing to let out land submit details of their reservation price to the auctioneer. All bids and reservation prices are attributed to farm profitability.

Many of these characteristics of the ABM model are similar to those of a traditional farm-level equilibrium model but with no assumptions of a single market clearing price. Furthermore, we assume that transactions take place under an iterative sequential process rather than occurring instantly at an equilibrium price.

In the ABM model, limits are placed on the extent to which farms can acquire additional land and no farm exits are permitted. It is assumed that these limits can be enforced by a central authority at the regional or national level. This institution may carry out a role similar to the SAFER (Sociétés d’Aménagement Foncier et d’Établissement Rural) organisation in France (e.g., Boinon, 2012 and Piet et al., 2012) or the CDOA (Commission Départementale d’Orientation Agricole) whose role in the French agricultural land market is described in (Piet et al., 2021). It is assumed that the Central Authority closes the land rental market when the rental share reaches 30 per cent of utilizable agricultural area in each region. A more significant increase in the rental share would probably require a significant number of farm exits and the emergence of a larger pool of non-farming landowners. Land tenure in Ireland is dominated by owner-farmers (Swinnen et al., 2016). However, there are strong indications of a change in attitude among landowners towards letting out land with a considerable number of farmers open to the possibility of letting out some land (Geoghegan et al., 2021).

The assumption of no farm exit appears to be a realistic assumption given that farmers in Ireland to tend have a strong resistance to the idea of retirement (Conway et al., 2022). Preliminary results from the 2020 Census of Agriculture point to a small reduction in the number of farm holdings in Ireland between 2010 and 2020 thereby indicating a low rate of farm exit (CSO, 2022).

At the end of the auction period, the model calculates the farm size concentration using various distributional statistics including the Gini coefficient (Gini, 1921). Previous research by Freeman et al. (2009) used an agent-based modelling approach to analyse the evolution of the farm size distribution in Canada between 1960 and 2000, finding among other things that farms with an initial land holding greater than the mean were significantly more likely to survive and grow relative to the smaller farms with an initial holding size below the mean.

Similar to Viaggi et al. (2013), the farm profits (including subsidies) determine the formation of bid prices (of potential tenants) and asking prices (of landowners). In this approach, the ABM is not entirely detached from the traditional farm equilibrium model. However, we do not assume in the ABM model, that rental prices are determined solely by aggregate supply and aggregate demand as would be the case under the standard walrasian equilibrium model.

Design Concepts

In this section, we describe the design concepts behind the ABM model. These design concepts are based on the elements described in (Grimm et al., 2006; Grimm et al., 2010). This ABM model is relatively simple. However, the benefits of using the ODD protocol are still important for such a simple model so that readers can understand what is excluded from the model (Grimm et al., 2010).

Basic Principles

The model is used to simulate the impacts of an increase in profit maximization behaviour from an initial state where profit maximization is not the main determinant of the land distribution. The ABM model assumes that profit maximization becomes the dominant driver of land transfer during the simulation stage.

The assumption of the initial state of the ABM model is supported by a long history of research on agricultural land transfer in Ireland emphasising the importance of land inheritance and farm succession within the family farm household (Conway, 1986; Kennedy, 1991; Leonard et al., 2017). Many of the assumptions from neo-classical microeconomic theory are retained. These include the axioms of non-satiation (more is better), completeness (full knowledge of available land parcels, their characteristics and the ability to compare parcels) and transitivity. These assumptions reduce the degree of complexity in the model making it more manageable.

However, the introduction of a central authority places limits on the extent to which large farms can participate in land rental markets. In the initial state, approximately three per cent of farms are excluded from participating in the market due to their initial farm size. In addition, it is assumed that the land rental market comes to a close when the land rental share in the region reaches 30 per cent. All landowner-farmers retain some amount of land so that farm exits are not permitted. These conditions limit the influence of the above strong neo-classical assumptions. The inclusion of the 30 per cent cap on the regional rental shares is necessary to prevent the model from simulating farm exits. A cap of 40 per cent could only be achieved via farm exits in some regional markets.

Emergence

At the system-level, the farm structures and the extent of farm size concentration can change significantly. These phenomena can emerge due to a change in individual behaviour towards the land market with more land becoming available to rent. Certain system-level phenomena are imposed on the model. It is assumed that farms remain in their current farming system. The changes in farm structures can therefore emerge because of changes in the size of farms within different systems rather than due to a change in the number of farm holdings in each system.

Adaptation

Adaptation plays a limited role in this model. It is largely assumed that farmers will reproduce observed behaviours in terms of their farming operations e.g. livestock intensity per unit of land, choice of crops and the selection of various inputs. However, farmers who expand beyond a certain threshold are assumed to encounter additional costs associated with the purchase of new machinery, livestock and buildings. This impacts negatively on their capacity to bid for additional parcels of land. In addition, these limits can reduce the number of farms simulated to expand to the maximum size threshold.

Objective

Tenant farmers have the objective of acquiring additional land within their region at the lowest possible price. Landowners are motivated to increase the returns from owning land by letting out land to potential tenants. At the same time, these landowners have another objective of continuing to actively farm on a smaller proportion of their land.

It is assumed that tenant farmers make their decisions based on the rental price of each land parcel. The determination of this land rental price is described in the appendix as it is not the main focus of this paper. At the same time, landowners wishing to let out some of their land are motivated to attain the highest possible price. The duration of the land rental contract does not feature in this model. In reality, the duration of the contract and other non-price characteristics could play important roles in the land market participation decisions.

Fitness

In this model, the fitness is essentially determined by farm profitability. We describe the determinants of farm profit in more detail in the details and methods section.

Prediction

It is assumed that the recent history of farm profitability is used to form predictions about future profitability and these predictions underline the bids and reservation prices for particular land parcels. The model does not deal with the uncertainties around land use changes including the possible influence of urbanisation or potential flooding.

Interaction

It is assumed that interactions between landowners and potential tenants largely take place via the auctioneer (Figure 1). Potential tenants are fully aware about the availability of land parcels in their region. However, it is assumed that social interactions between landowners and tenant farmers do not play any role in influencing the bidding process and in determining the precise conditions agreed under a given land rental contract.

Collectives

It is assumed that landowners and tenant farmers act independently. Until recently, there is limited evidence of collectives playing an important role in influencing agricultural land rental markets in Ireland. However, corporate entities or family farm partnerships may be playing an increasing role in land markets (SCSI/Teagasc, 2022). A distinction is made between landowners who are willing to rent out land and tenant farmers who are willing to rent-in additional plots of land.

In this section, we provide details on the methods applied in the ABM model. The details form the third category of the ODD protocol. This category has three elements 1) Initialization 2) Input data 3) Submodels.

Initialization

In order to carry out the simulations, we first divide the sample of Teagasc National Farm survey farms into six groups based on two soil quality categories (good and medium soils) and three regional categories. Farmers and Landowners operate within their regional market. We exclude the farms with poor soils due to the low sample size. This essentially means that the reported land area and rental area for farms in poor quality land will not be altered as a result of the simulations. The definitions of soil quality are detailed in the appendix.

In forming regional categories, we distinguish between the following:

Border, Midlands and West NUTS 2 region,
the combination of the South-West and Mid-West NUTS 3 regions,
the combination of the NUTS 3 South-East, Dublin and Mid-East regions.

The following details about the input data give more insights into the initial state of the model including the land markets in each region.

Input Data

The main data source is the Teagasc National Farm survey. These data are frequently used to determine the broader financial situation on Irish farms and contribute to economic and rural development research and policy analysis. These data include the level of gross output, costs, income, investment and indebtedness across the spectrum of farming systems and sizes. The data form the Irish component of the Farm Accountancy Data Network (FADN) database, which is used to evaluate farm incomes and the impacts of the Common Agricultural Policy across the EU for the EU Commission.

A farm accounts book is recorded for each year on a random sample of farms, selected by the Central Statistics Office, throughout the country. In order to ensure that the sample is representative of the farm population at a national level, the farms in the sample are selected at random from strata (categories) in the farm population. These strata ensure that the sample contains an appropriate mix of farm types and that the economic size (measured in farm output) of the farms selected is also representative of the population. Each farm in the sample is accorded a weighting factor and this means that each farm in the sample is representative of a specific number of farms in the population (Dillon et al., 2022).

Our models are based on Teagasc NFS data for the period 2015 to 2017. For 2017, there are 896 farms included in the data, representing approximately 92,847 farms nationally. The simulations are applied to all farms with good or medium soils. In 2017, there are 827 farms with either good or medium soils, representing approximately 85,115 farms nationally and these 827 farms form the sample for this study.

The panel is unbalanced in the sense that there is some attrition from year to year as farmers leave the sample and are replaced by other farms. The attrition rate is relatively low and a sizeable proportion of the farms are contained in the dataset for all of the years concerned. We find that 794 farms have three observations from the period 2015 to 2017 and 735 of these farms are located on medium or good quality soils. New farmers are introduced during the period to maintain a representative sample and the sample size for all farms is usually kept to between 850 and 1000 farms.

Table 1 provides some summary statistics relating to each of the six land market regions. In terms of the land area represented, the largest regional market is the BMW region with medium quality land (881,532 Ha.). The smallest regional market is the market combining the south-west and mid-west with medium quality land (284,190 Ha.). There is some variation in the rental shares between each of these markets. The rental share is highest in the East region with good quality land (21.9%). This is likely to be influenced by the prominence of tillage farming in the region. The rental share appears to be lowest in the BMW region with good quality land (15.6%).

Table 1

Summary Statistics for Six Regional Markets

Region	Soil Quality	No. Farms	Weighted No. Farms	UAA (Ha.)	Rental Share
South-West, Mid-West	Good	115	9,470	428,760	16.5%
East	Good	194	17,400	822,733	21.9%
BMW	Good	167	19,366	773,374	15.6%
BMW	Medium	200	25,532	881,532	20.3%
South-West, Mid-West	Medium	76	6,920	284,190	16.8%
East	Medium	75	6,427	318,104	18.4%

Source: Authors calculations using Teagasc National Farm Survey from 2017.

The number of farms (unweighted) is relatively small in all regions. The BMW region with medium quality land (200) is the group with the largest number of farms while the East region with medium quality land has just 75 farms.

In Table 2, we show rental price statistics for each of the six land markets. These statistics represent the initial state of the land rental market and show that the median rental price is highest in the south-west and mid-west regions with good quality land. Interestingly, the median rental price is higher for medium quality land in the south-west and mid-west relative to good quality land in the BMW region. Within each region, there is considerable variability in land rental prices as indicated by the 25^th and 75^th percentiles.

Table 2

Rental Price Statistics for Six Regional Markets

Region	Soil Quality	Median Rented Price (€)	25^th Percentile of Rented Price	75^th Percentile of Rented Price
South-West, Mid-West	Good	362	250	441
East	Good	354	250	431
BMW	Good	252	209	355
BMW	Medium	223	150	291
South-West, Mid-West	Medium	314	240	410
East	Medium	250	222	357

Source: Authors calculations using Teagasc National Farm Survey from 2017.

Submodels – Theory

We outline our two key hypotheses. Fagiolo et al. (2019) explain that the empirical validation of agent-based models has made ‘substantial advances’ but more research is required in advancing hypothesis testing.

We firstly hypothesise that an increase in profit maximisation behaviour will lead to an increase in the farm size concentration and inequality. This may be reflected in a number of alternative measures of farm size concentration and inequality. We seek to verify this hypothesis using the ABM model.

Secondly, we form a hypothesis in relation to the type of inequality change. Jäntti and Jenkins (2015) explain that pro-poor growth does not guarantee inequality reduction, because it may also lead to re-ranking whereby initially poor individuals move strongly up the income distribution with initially richer households moving swiftly down the distribution. Conversely and in the context of this research, an increase in inequality may be considered progressive if the farm size growth favours initially small farms at the expense of initially large farms. Similar to the income inequality literature of Jenkins and Van Kerm (2009), we examine whether or not the change in the distribution can be considered progressive (i.e. whether farm size growth favours the initially small, medium or large farms).

We hypothesise that an increase in profit maximisation behaviour could lead to either a progressive or regressive change in the farm size distribution. This is reasoned by the relatively low volume of land sales transaction in Ireland and the sparse (until recently) land rental markets (Loughrey et al., 2020). Land inheritance is the dominant source of land transfer and profitability is therefore not considered to be the main determinant of the initial farm size. We stress that the initial state of the land market (2015-2017) represents a combination of profit maximising and non-profit maximising behaviour where the latter is influenced strongly by the motivation for inter-generational transfer of land within the family, the preservation of the family farms and the societal norms underpinning the family farm (Cassidy, 2019).

We begin with the understanding that the farm size of each farm may be comprised of rented land or owned land. We formalise according to Ciaian and Swinnen (2006), the land decision-making problem of a profit-maximizing individual farm in the following:

M a x π_{i} = p f (a^{r e n t - i n} + a^{o w n}) - (r + t) a^{r e n t - i n} + (r - t) a^{r e n t - o u t}

where p is the price of farm output, r is the rental price of land, t represents transaction costs, $a^{rent-in}$ is the amount of land rented-in by the farmer, $a^{rent-out}$ is the amount of land rented-out by the farmer, $a^{own}$ is the amount of land owned by the farmer.

The transaction costs $t$ can be associated with information, negotiation and the enforcement of contract provisions. In land rental contracts, the adoption of a long-term contract can reduce the costs associated with the renegotiation of contracts. The inclusion of non-price provisions such as a break clause can provide some level of flexibility for the contracting parties in entering into a long-term contract (Adenuga et al., 2021). The transaction costs are likely to vary between farms due to differences in the contract duration and the level of experience in contract negotiation.

In the ABM model, we do not assume that the initial state of the land market is perfectly competitive. This means that participation in the agricultural land market can bring about improvements in farm household economic welfare, relative to the initial state. We assume that the same production function applies to both land rented and land owned and that total farm size equals the sum of land rented-in and owned minus land rented-out.

A = a^{r e n t - i n} + a^{o w n} - a^{r e n t - o u t}

By behaving according to the profit maximization motive, farm operators with a marginal value product of land higher than the marginal cost of land (r+t) will tend to rent-in additional land.

In the sealed-bid auction setting of this model, potential tenants compete for rented land and this competition ensures that the rental costs approach the value of the marginal product of the land. However, we do not assume that the rental price will be in a state of equilibrium, but rather that there is a tendency towards equilibrium.

(p \frac{\partial f (A)}{\partial (A)}) \Leftarrow (r + t)

It is assumed that a market agent or auctioneer coordinates between landowners and potential tenants. This market agent collects all available information on sealed bids and reservation prices and identifies the highest bidder for each land parcel available on the market and mediates between landowners and tenants in finalising the agreed rental price. An important assumption in this model is that each farmer makes only one sealed bid for each parcel of land.

In contrast to the traditional farm equilibrium model, we do not assume that prices are negotiated at a single point where aggregate supply and aggregate demand are intersecting. For the individual tenant farmer, the marginal product of the land equals the rental price plus transaction costs plus a surplus $s$ to the tenant farmer. This surplus allows the tenant farm operator to earn a profit from renting-in additional land. A tenant farmer may achieve a surplus from renting-in additional land where the marginal value product of the land exceeds the market rate for the rented plot of agricultural land.

p \frac{\partial f (A)}{\partial (A)} = (r + t + s)

In addition, we attempt to account for diminishing returns to scale. We estimate additional costs associated with expanding the land area by 20 hectares or more. It is assumed that increasing the land area beyond this threshold will necessitate additional building costs and further costs associated with operating and maintaining those buildings and potential interest expenses associated with the purchase of livestock.

Equation 5 shows that for the supply side of the market, the transaction costs are subtracted from the rental income. The model assumes that a large pool of landowners are willing to let out their land at a given time. The resulting competition between landowners is assumed to reduce rental prices so that they approach the value of the marginal product of the land. As in the case of tenant farmers, landowners may achieve a surplus where the market rate exceeds the willingness to accept, which is based on the marginal product of the land under the current ownership.

p \frac{\partial f (A)}{\partial (A)} \Leftarrow (r - t)

There are a number of constraints in the ABM model. In this model, farms may not always expand to the point where the marginal product and marginal costs of the land are equal. It is assumed that a central authority closes the auction when the share of rented land in a region reaches 30 per cent of the utilizable agricultural area in that region. In the ABM model, we exclude the option of farm exit so that farms with very low or negative returns remain active in farming. In the equilibrium model, farm exits are permitted and the number of remaining farms can reduce significantly. Within each land market group, we make the strong assumption that land parcels are homogenous and that differences in gross margins are due to variability in farm management.

Similar to Viaggi et al. (2013), we simulate transactions in the land market assuming that farms seek to maximize total farm profit under the further assumption that land can be reallocated among a group of farms within a particular region or local area.

M a x \prod = \sum_{i} π_{i} (a_{i}, {u_{i}, x}_{i})

subject to

\sum_{i} a_{i} \leq A

Where $\prod$ is the total farm profit in the region, $\pi _{i}$ represents the profit function of farm i, $a_{i}$ represents the land available in farm i and x represent other factors affecting farm profitability. In the ABM model, the term $u_{i}$ represents the land, which is unavailable to the market as all farms retain a minimum number of hectares.

In the ABM model, there is a constraint so that no farm is simulated to fall below ten hectares in land area. The land which is potentially available to the market $a_{i}$ is therefore constrained to be the Utilizable Agricultural Area (UAA) of each farm in the sample minus 10. The land available to the market equals zero for the case of a farm with an initial farm size, which is less than 10 hectares.

α_{i} = M a x (0, {U A A}_{i} - 10)

This can be contrasted with the equilibrium model, where the available land equals the total utilizable agricultural area of the region i.e. $\underset{i}{\sum }a_{i}=\sum UAA_{i}$ . Farm exits are permitted in the equilibrium model and all farmland can potentially form part of a transaction.

Demand

In the ABM models, we place limits on the demand for agricultural land rental. The ABM model stipulates that no dairy or livestock farm can participate in the land rental market when farm size exceeds 120 hectares. For tillage farms, the model stipulates that no farm can participate in the land rental market when farm size exceeds 200 hectares. The higher threshold for the tillage sector is due to the greater land intensity on tillage farms. These assumptions also apply to the traditional equilibrium model.

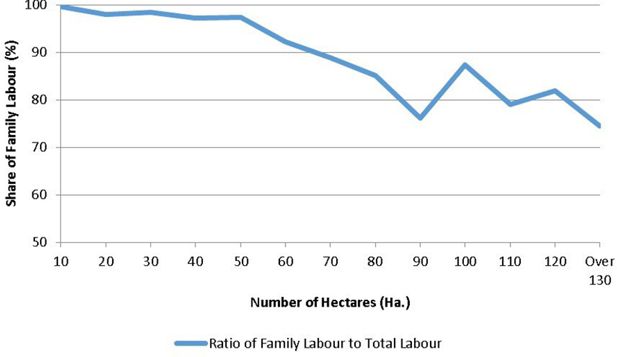
These thresholds are designed in order to remain within the scope of the family farm model. We specify that these thresholds may allow a majority of the farm labour to be attributed to the farm operator and other family members. Garner and de la O Campos (2014) conclude that the reliance on family labour is the most defining characteristic of family farms”.¹ In the appendix, we show in Figure A2, the share of family labour in total labour according to the farm size.

The individual demands for additional agricultural land $d_{i}$ can be therefore described in the following:

Dairy and Livestock $d_{i}=Max\left (0,120-UAA_{i}\right)$ (9)

Tillage $d_{i}=Max\left (0,200-UAA_{i}\right)$ (10)

We attempt to simulate land transfers based on a scenario where profit maximisation is the only motive for new transactions. It can be noted that other non-pecuniary motivations influence land-use decisions (Howley, 2015; Howley et al., 2015). However, these motives are assumed to not influence new land rental transactions.

Similar to the case of Balmann (1997) and Freeman et al. (2009), the marginal value product of land is based on the expected gross margin of each individual farm. We estimate the adjusted gross profit per hectare for each individual farm in each of the six regional groups. This adjusted gross profit per hectare is the gross revenue per hectare plus an adjustment for direct payments minus variable costs and family labour costs and is described in equation 11. Non-family labour costs are already deducted as part of the variable costs. The adjusted gross profit per hectare does not necessarily represent the shadow price of land due to the possibility of immediate constraints relating to the hiring of labour or purchase of machinery.

We do not account for the influence of the riskiness of the farm returns in the formation of bid prices. The maximum willingness to pay or bid price from each potential tenant farmer is influenced by the direct payments and the extent to which these payments are capitalised into the bids of each potential tenant. Previous research has not given much attention to the capitalisation of direct payments into the formation of bid prices. Viaggi et al. (2013) is among the few exceptions. The complexity and uncertainty around the estimation of capitalisation rates is a likely contributor.

In the baseline scenario, we assume that 50 per cent of direct payments are included in the value of each bid. This does not necessarily translate into a capitalisation of direct payments of 50 per cent given the interactions with the supply side of the market.² The bid price or maximum willingness to pay from each tenant is therefore given in the following:

{{P r i c e}_{B I D} = π}_{G R O S S} = \frac{A O - V C - F L C}{a} + c D P h a

Where $P_{bid}$ is the maximum willingness to pay equal to the $\pi _{GROSS}$ gross profit per hectare. The notation AO represents the value of agricultural output, VC represents variable costs, FLC represents family labour costs, which includes the estimated labour costs associated with the farm operator and other family members. The notation c represents the capitalisation rate and $D P h a$ represents the value of the direct payments per hectare.

In the ABM model, it is assumed that the variable costs per hectare increase when the newly acquired land exceeds 20 hectares. This is attributed to the additional building costs, energy costs and interest costs associated with the purchase of livestock. These additional costs affect the assumed willingness to pay for additional farmland. For dairy farms, the assumed decrease in willingness to pay is €200 per hectare and for livestock farms, the assumed decrease is €100 per hectare. There is some reasoning behind these values. We assume that farmers account for the building costs over a ten year horizon. Ryan and Lenehan (2016) outline the costs associated with winter accommodation for non-dairy beef animals and show how these costs vary according to the type of animal. Teagasc (2017) outlines the building costs associated with the construction of a new milking parlour and accommodation. The overall building costs for dairy tend to greatly exceed that of non-dairy cattle farming.

Within each of the six land markets, each farm is ranked according to their respective gross profits. In the ABM model, all farms with a size greater or equal to 12 hectares are ranked. The farm with the lowest gross profit offers their land for leasing to a potential tenant. The market agent collects the bids and allocates parcels to the farm in the market with the highest adjusted gross profit per hectare. Farms exit the market if they reach the thresholds outlined in equations (9) and (10).

Microsimulation Model

It is assumed that each farm has the same strategy i.e. rent-in land at the cheapest possible price or alternatively let-out land at the highest possible bid price. In this sealed-bid auction, the most profitable farms will seek to rent-in parcels at the lowest possible price from the farms with the lowest profitability. At the same time, the farms with relatively low profitability will seek to let-out land to the highest bidder i.e. from the farm with the highest gross profit per hectare.

The simulation process begins by transferring agricultural land from the least profitable farm to the most profitable in an iterative process. All transfers take place within the same regional land market and no tenants enter into regional markets outside of their own region. In this process, we assume that land is transferred in a parcel size of two hectares. As described in (9) and (10), the model is constrained so that farms exit the land rental market when their farm size reaches a certain threshold.

Meisser (2017) advices that ‘source code cannot replace high level descriptions, but it should be the preferred way to provide the full model specification’. In the appendix, we therefore include a portion of the source code with the pseudo-code to help understand the model implementation in Stata. We also include the source code for the ABM model in a separate file containing the variable name definitions.

In this simulation model, the land rental market closes at the point where the rental share in the region reaches 30 per cent. This would bring the rental share closer to the levels reported in many Western European countries (Loughrey et al., 2020). It should be noted however, that the rental share in Ireland is unlikely to reach the levels reported in EU member states such as Germany and France given that landowners and farmers are largely the same population.

4.Results

In this section, we detail the results from our simulations and add some findings based on recent data from the 2020 Teagasc NFS data. We display the simulation results showing the simulated change in the farm size distribution and the extent of land transfer from the livestock sectors to the dairy sector. In line with our second hypothesis, we identify whether or not the simulated change in the farm size distribution can be described as progressive or regressive. We pay some attention to the determination of prices in the equilibrium model.

In Tables 3 and 4, we show the simulated changes according to each farming sector. Table 3 shows that under the simulation model and with the greater emphasis on profit maximization, the average farm size in the dairy sector increases by 15.2 hectares while the average farm size in the cattle sector declines by 5.9 hectares and the average farm size in the sheep sector by approximately 8.7 hectares. Table 4 shows the implications for the share of agricultural land allocated to each farming system. One can see from the results that the share allocated to the dairy sector increases from 23 per cent to 30.5 per cent of agricultural land in Ireland.

Table 3

Simulated Average Farm Size by System

System	Average Farm Size (Ha.)	Average Farm Size [Post-Simulation]	Change in Farm Size (Ha.)
Dairying	58.4	73.6	15.2
Cattle	33.5	27.6	-5.9
Sheep	46.9	38.2	-8.7
Other	73.7	83.5	9.8
Tillage	59.1	64.8	5.6

Source: Teagasc NFS 2017 and Author’s simulations using Teagasc NFS 2015-2017.

Table 4

Simulated Share of Agricultural Land by System

System	Initial Share	Share Post-Simulation	Percentage Change
Specialist Dairying	24.0%	31.5%	7.4%
Cattle	46.0%	39.3%	-6.7%
Sheep	17.1%	14.4%	-2.6%
Other	2.5%	3.0%	0.4%
Tillage	10.3%	11.8%	1.4%

The Farm Structures Survey showed that the total rented hectares for specialist dairy farms increased by approximately 30,000 hectares (approximately 0.6 per cent of total agricultural area) between 2013 and 2016 (CSO, 2022). The preliminary results for the 2020 Census of Agriculture show that the total UAA farmed by specialist dairy farms increased by 4.7 per cent from approximately 952,000 hectares in 2016 to approximately 997,000 hectares in 2020 (CSO, 2022). This indicates that the share of land farmed by dairy farms increased by approximately 0.2 per cent per annum during this time.

These preliminary Census results also show an increase in the average UAA on dairy farms in Ireland from approximately 55 hectares in 2010 to 65 hectares in 2020. This indicates that the rise in the average dairy farm size is already well underway. It is not surprising that average dairy farm size is increasing in the aftermath of quota abolition in 2015. The extent of the rise in average dairy farm size may be influenced to some extent by the increasing prevalence of company farms. This can be difficult to capture using FADN data where the survey coverage is concerned with family farms.

Table 4 shows that in the case of the cattle sector, the share of agricultural land declines from 44.7 per cent to 38 per cent. The share of land allocated to the sheep sector declines to 14.5 per cent. An increase occurs in the tillage sector where the share rises to almost 13 per cent of total land area. These simulation results appear to be larger than the changes indicated by the 2016 Farm Structures Survey and the preliminary results from the 2020 Census of Agriculture (CSO, 2022).

The increase in average dairy farm size does not necessarily correspond with an equal increase in the share of land in dairy farming. This is due to the possibility of dairy farm exits. It appears from the 2020 Census of Agriculture that the number of specialist dairy farms in Ireland decreased between 2016 and 2020. It may be the case that an increase in profit maximization behaviour is occuring among dairy farmers who are considering exiting the dairy farming system. Some of these farmers may be opting for the decision to lease out land when exiting dairy farming.

The above results are based on simulations representing a scenario where profit maximization becomes much more important in the decision-making of landowners and tenants relative to the recent past. There is no particular timeline placed on the speed of this change in decision-making. However, some validation appears necessary. The simulations have produced striking changes in the distribution of farmland and it is important to examine whether or not there are some signs of a changing distribution. In addition, there is the possibility that the comparison of simulated and actual data will lead to further insights and directions for future research.

In Table 5, we use 2020 Teagasc National Farm Survey data to show the estimated changes in the average farm size by farming system. The results are presented using the 2017 sample weights and with the 2020 sample weights. These results indicate a clear increase in the average farm size of specialist dairy farms and particularly when the change in sample weights are taken into account. The Teagasc NFS sample weights for 2017 are based on the Farm Structures Survey 2016 data and the 2020 weights are based on the CSO (2022) data. An increase in dairy farm size was identified in the latter. This necessitated an increase in the weight for larger dairy farms.

Table 5

Change in Average Farm Size by System 2017 to 2020

System	Average Farm Size 2017 (Ha.)	Average Farm Size 2020 [Ha.]	Change in Farm Size (Ha.)	Average Farm Size 2020 [Ha.]	Change in Farm Size (Ha.)
		2017 Weights		2020 Weights
Dairying	58.4	61.7	3.3	65.9	7.5
Cattle	33.5	33.6	0.1	31.5	-2.0
Sheep	46.9	47.3	0.4	49.5	2.6
Tillage	59.1	61.7	2.6	73.2	14.1

Source: Teagasc NFS 2017 and 2020.

Table 5 indicates that the average farm size of a specialist dairy farm in Ireland is 7.5 hectares larger in 2020 relative to 2017. Using a balanced panel and fixed 2017 sample weights, the increase in average farm size is just 3.3 hectares. However, it is important to take into account the change in sample weights as these capture the change in the actual size distribution over time as indicated by the Census of Agriculture. Relative to the simulation results, the changes in average farm size appear smaller for both cattle and sheep systems. Sheep farming has improved significantly in terms of economic performance since 2017 (Dillon et al., 2022) and this may be a factor in the expanding farm size. The results for the tillage system may be influenced by a relatively small sample size and changes in the composition of the sample. We do not report the results for the Other category due to the small sample size. Under the balanced panel, the average tillage farm is slightly larger (2.6 hectares) in 2020 relative to 2017. Our ABM model does not account for the possibility of a change in the relative returns from different farming systems and this remains a limitation in the model.

Table 5 indicates that the average farm size of cattle farms has declined slightly by 2 hectares during a three year period and this could be due to a myriad of factors. In addition, there is evidence of some exits from cattle farming and exits from farming in general. The 2016 Farm Structures Survey showed 78,300 farms in specialist beef production but this declined to 74,159 in the 2020 Census of Agriculture. At the same time, the total number of sheep farms has increased from 15,100 in 2016 to 17,435 in 2020. A combination of farm exits and a change in farming systems are probably contributing to the actual decline in agricultural area associated with non-dairy cattle farming.

In Table 6, we use Census of Agriculture data for 2010 and 2020 to further explore the actual changes in the agricultural land area allocated to each farming system. These definitions differ from the Teagasc NFS survey in terms of the treatment of crop systems and mixed crop and livestock systems. However, the results are very striking in showing the large changes in land area by farming system from 2010 to 2020. Over this ten-year period, there has been a 15.2 per cent increase in the land area for specialist dairy farming and a 7.4 per cent decrease in the area allocated to specialist beef production. For dairy farming and non-dairy cattle farming (i.e. specialist beef production), the simulated changes described in Table 4 are still higher than the actual changes that have taken place between 2010 and 2020. However, there is a clear increase in land rental activity at the end of this decade. Table 6 indicates that large changes in land use can take place within a relatively short period of time. However, the comparison of 2017 and 2020 data (Table 5) may be too short of a window for large changes to be expected.

Table 6

Total Agricultural Area by Farming System 2010-2020

System	2010 (Ha.)	2020 (Ha.)	Change (Ha.)	Percentage Change	Percentage Change in Share of Land
Dairying	865,666	997,267	131,601	15.2%	3.2%
Cattle	2,153,343	1,994,877	-158,466	-7.4%	-2.9%
Sheep	417,494	503,872	86,378	20.7%	2.0%
Tillage	268,520	290,461	21,941	8.2%	0.6%
Mixed Grazing Livestock	527,622	381,158	-146,464	-27.8%	-3.1%
Mixed Crops And Livestock	137,541	114,159	-23,382	-17.0%	-0.5%
Mixed Field Crops	162,832	186,559	23,728	14.6%	0.6%
Other	33,038	37,077	4,039	12.2%	0.1%

Source: Censuses of Agriculture 2010 and 2020.

In Table 7, we return to the simulation results and show the simulated impact on farm size inequality. These results suggest that farm size inequality would increase in all regions but the increase appears greatest in two of the markets where the soil is of medium quality. This confirms the first hypothesis that an increase in profit maximisation leads to an increase in farm size inequality. The simulation results are somewhat sensitive to the choice of the upper threshold, which restricts larger farms from entering the market. The gini coefficient is three to four points lower in some regions if we apply an upper threshold of 90 hectares for dairy and livestock farms. We have also tested the implications of running the model with the expected gross margins based on the longer period of 2012 to 2017. The results are not found to be very sensitive to the choice of reference period.

Table 7

Farm Size Inequality by Group under Profit Maximisation

Group	Region	Soil Type	Initial Gini Coefficient 2017 Data	Gini Coefficient [Simulation]	Gini Coefficient 2020 Data
1	South-West, Mid-West	Good	35.8	45.0	36.8
2	East	Good	39.8	47.4	42.8
3	BMW	Good	36.2	50.8	42.7
4	South-West, Mid-West	Medium	31.7	48.9	37.4
5	East	Medium	32.4	49.9	38.1
6	BMW	Medium	32.4	41.8	38.0

The farm size inequality would rise from being relatively low in comparison to other EU member states (Loughrey and Donnellan, 2017). This outcome would occur in the absence of counteracting forces such as generational renewal and the influx of new entrants, who may contribute differently to the extent of concentration. In practice, the extent of the distributional change is also likely to be tempered by the preferences of the older generation in maintaining active control of the farm, a process that is described in Conway et al. (2017) and Conway et al. (2021). We compare the simulation results with the findings from the 2020 Teagasc NFS data. In all groups, there appears to be some increase in farm size inequality between 2017 and 2020 but not to the same extent as the simulation results. The increase in the gini coefficient appears highest in the BMW region and where the land is of medium quality in the south-west, mid-west and east regions. The Gini coefficient can be sensitive to the inclusion of very small farms in the survey and we therefore consider alternative indicators of farm size concentration.

For the estimation of farm size concentration, we estimate the mid-point hectare statistic at the regional and national level as described in (Lund and Price, 1998). This statistic is perhaps better suited to assessing farm size concentration than the Gini coefficient as the former is less sensitive to the inclusion/exclusion of small farms from the survey.

Table 8 shows the simulation results for the mid-point hectare statistic. These indicate large increases in farm size concentration in most of the regions. The largest increases in farm size concentration are in the south-west and mid-west regions where a large number of medium-sized specialist dairy farms expand to 120 hectares. This indicator is probably better suited to the analysis of farm size concentration than the Gini coefficient as the latter is more sensitive to the inclusion of very small farms.

Table 8

Mid-Point Hectare Statistic by Group under Profit Maximisation

Group	Region	Soil Type	Initial Midpoint Hectare	Midpoint Hectare [Post-Simulation]	Midpoint Hectare 2020
1	South-West, Mid-West	Good	58	73	67
2	East	Good	64	77	66
3	BMW	Good	45	67	59
4	South-West, Mid-West	Medium	47	72	50
5	East	Medium	62	91	64
6	BMW	Medium	40	46	41

Under the assumption of profit maximization behaviour, this further expansion in milk production is facilitated by the decisions of a large number of drystock cattle farms to let out the majority of their land. In the East, the midpoint hectare increases from 64 to 77 hectares in good quality land areas and from 62 to 91 hectares in areas of medium quality land. In the south-west and mid-west, the midpoint hectare increases from 58 to 73 hectares for good quality land and from 47 to 72 hectares for medium quality land. In the BMW regions, the farm size concentration appears somewhat lower. This is due to the presence of a large number of small cattle and sheep farms. In the BMW region, the midpoint hectare increases from 45 hectares to 67 hectares in the case of good quality land and from 40 hectares to 46 hectares in the case of medium quality land.

In the final column, we show the estimated midpoint hectare based on the actual Teagasc NFS data for 2020. These figures indicate an increase in farm size concentration in two regions with good quality land and limited changes in regions with medium quality land. The increase in concentration is most notable in the BMW region (+14 hectares) and in the South-West and Mid-West region (+15 hectares). These results are robust to the use of a balanced panel dataset. The limited change in farm size concentration in other regions may have some positive implications. The case for a more active land market may be less convincing for areas of medium quality land. In addition, the farm size concentration is already relatively high in the east region and further concentration may be less beneficial in economic and environmental terms.

Table 9 shows the extent to which the simulated rise in inequality can be considered progressive or regressive and whether the farm size growth favours the initially small or large farms. We find that in the South-West and Mid-West regions with good quality land, the increase in profit maximization behaviour in the land market would actually be progressive. The ABM model results indicate that an increase in profit maximization behaviour would lead to a slightly progressive change in the distribution of farmland in parts of the BMW region where the land is of good quality. There are some contrasting results for those geographical areas where the land is of medium quality with a regressive impact for medium quality land in the South-West and Mid-West regions and in the East region. In those areas with medium quality land, the farms in the 50-100 hectare size category would increase at the expense of smaller farms.

Table 9

Progressivity or Regressivity of Distribution in Post-Simulation

Group	Region	Soil Type	Progressivity+ Regressivity-
1	South-West, Mid-West	Good	+0.047
2	East	Good	-0.006
3	BMW	Good	+0.013
4	South-West, Mid-West	Medium	-0.059
5	East	Medium	-0.059
6	BMW	Medium	+0.029

Results for the Equilibrium Model and Price Determination

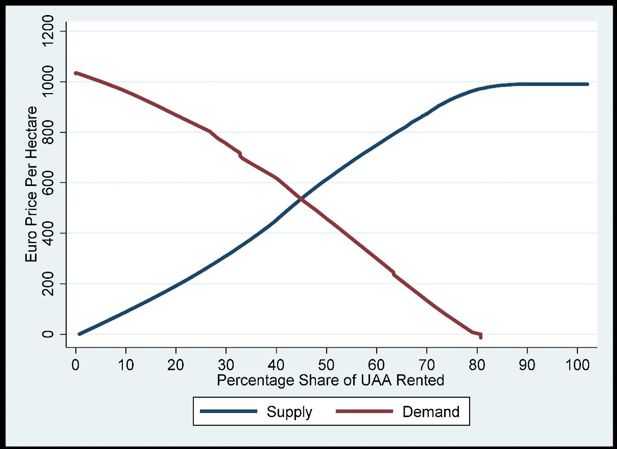
The ABM model can be useful in tracking changes in the farm size distribution but is limited in addressing the determination of land rental prices. This is partly due to the small sample size. We therefore describe the land market with a walrasian equilibrium model where prices are determined at the point where total supply equals total demand at the regional level. Figure 2 shows the supply and demand for agricultural land with good quality land in the south-west and mid-west regions under this equilibrium modelling approach. These graphs are constructed using the twoway and lowess commands in Stata in order to smooth the data. Figure 2 shows that the equilibrium price in this market is approximately €550 per hectare, where approximately 40 per cent of the land area is rented. The demand curve shows that many of the bidders in this market would be willing to pay amounts in excess of €600 per hectare for land.

Figure 2

Download asset Open asset

Market for Good Agricultural Land in South-West and Mid-West Region

Assuming that all transactions take place at the market clearing price, then some economic surpluses can be gained from renting-in additional land at the equilibrium price. At the same time, a significant number of low-income farmers could gain economically from renting out their land at the equilibrium price.

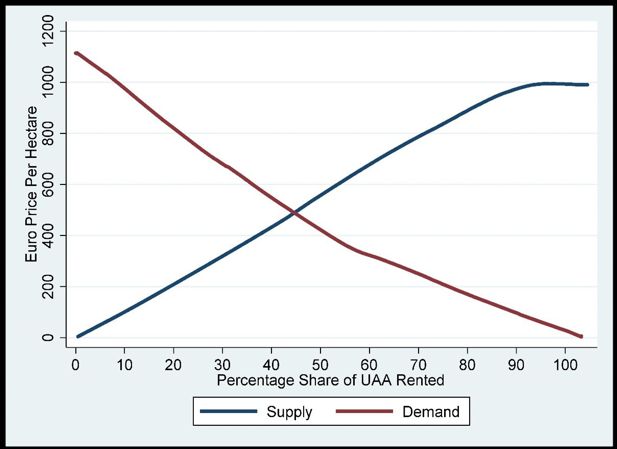
Figure 3 shows the equilibrium model for the East region with good quality land. In this market, the equilibrium price is similar to that shown in Figure 2. The demand curve shows that many of the bidders in this market would be willing to pay amounts in excess of €600 per hectare. Tillage farming is more prevalent in the east region relative to the south-west and mid-west region. It should be noted that land markets in this region tend to be more influenced by urbanization and non-agricultural usage.

Figure 3

Download asset Open asset

Market for Good Agricultural Land in East Region

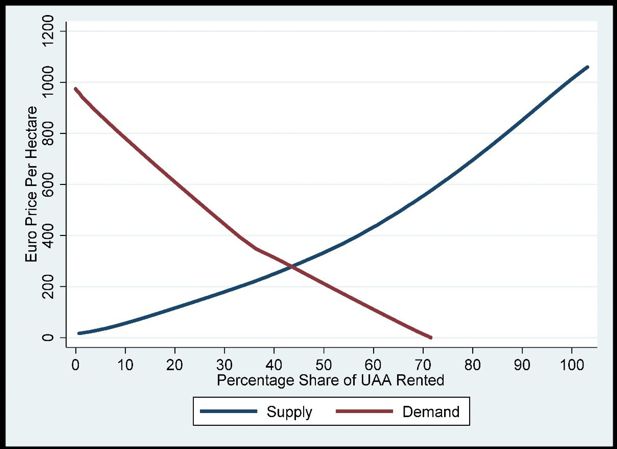
In Figure 4, we show the equilibrium model for the land market in the BMW region. This market contrasts sharply with the markets depicted in Figure 2 and 3. In the BMW region, there is a concentration of non-viable farms in the sheep and beef enterprises (O’Donoghue, 2017). This affects the shape of the supply curve in the land market under the assumption of profit maximization. The equilibrium rental price is much lower in this market relative to those other markets where there are good soils. Figure 4 shows an equilibrium rental price of approximately €300 per hectare, which is somewhat higher than the median price of existing rental agreements (€252 per hectare) as reported in Table 2. Although it is not shown in this paper, our results suggest that the equilibrium land rental price is significantly lower for the BMW region with medium quality land.

Figure 4

Download asset Open asset

Market for Good Agricultural Land in BMW Region

5. Discussion and Conclusion

In this paper, we have introduced a new agent-based microsimulation model to analyse the agricultural land rental market in Ireland. The findings from the microsimulation model indicate that a continued increase in profit maximization behaviour in the land rental market could lead to a sizeable shift in farming activity away from the non-dairy cattle and sheep farming systems to the dairy farming system with significant increases in farm size concentration. Census of Agriculture data for 2010 and 2020 shows that a significant shift in agricultural area has already occurred in terms of the area allocated to each of the main farming systems. Since 2016, it appears that the average dairy farm size has increased but with limited increases in the national share of farmland allocated to dairy farming. This can be explained by the exit of some dairy farms and the letting out or sale of these farms to other dairy farms. For expanding dairy farms, this source of additional farmland may be limited in the future and could force a greater reliance on renting or purchasing land from cattle and sheep farms.

The simulation results indicate that an increase in profit maximization would lead to the farm size distribution becoming more concentrated than is currently the case. This would occur with a rise in the rental share from approximately 20 per cent to 30 per cent of total utilizable agricultural area. The results contain some caveats. Some increase in the rental share could occur as a result of farmer retirements and farm exits and these are excluded from the ABM model. The simulated changes in the farm size distribution may also involve significant economic mobility in some regions. The distribution of farmland could follow a more meritocratic form where the land market becomes more influenced by profit maximization. In some areas with high land quality, the changes to the distribution could be mildly progressive where farm size growth favours initially small to medium sized farms.

At the same time, the ownership of farmland would remain unchanged thereby implying no change in the distribution of farmland ownership and associated wealth. Although not modelled explicitly, the findings suggest that older farmers with no successor may find the option of letting out good quality land appealing. The results suggest that the strength of the case for a more active land rental market is place dependent with less evidence in support of a more active land market in areas of medium land quality. Evidence from the 2020 Teagasc National Farm Survey data indicates that the increase in farm size concentration is largely occurring in areas of good quality land with limited changes in areas of medium quality land.

The model results also indicate that an increase in profit maximisation behaviour leads to a significant transfer of agricultural land from the cattle and sheep sectors and towards the more profitable dairy sector. The simulation results point to a small increase in land area for the tillage sector, which can be partly attributed to relatively lower labour costs and lower building costs associated with expansion of the land area. A comparison of 2016 Farm Structures Survey data and 2020 Census of Agriculture data shows that many of these trends are taking place albeit at a slower pace. There is an important exception in sheep farming, where the land area is actually expanding. This trend is a possible result of a notable improvement in economic conditions for the sector in recent years.

A number of potentially countervailing forces are excluded from consideration in the ABM model. For instance, the ABM model does not account for the potential of new entrants to alter the farmland distribution or the inclusion of the land sales market. In addition, the potential for farmers to change their farming system could have implications for the land rental market and the farmland distribution. Targeted changes to the system of farm subsidies could also have some implications for land rental markets both in terms of land rental prices and the farmland distribution. These factors are not considered in the current version of the ABM model.

In addition to the microsimulation model, we display results based on an equilibrium model, where prices are determined by the total supply and total demand for agricultural land and with the assumption of one single market-clearing price in each regional market. This provides some useful insights into the potential supply and demand for agricultural land in various regions. Under this equilibrium model of price determination, our results confirm sharp differences in rental prices between the land markets in the south and east regions and the largely disadvantaged BMW region in Ireland.

The microsimulation model and the equilibrium model can both be refined to account for the assumptions regarding transaction costs and the costs associated with fragmentation. Future work could account for the duration of land rental agreements, the possible influence of farm succession, the choice of farming system, the question of land sales, farm exit and the overall impact on farm incomes.

Footnotes

1.

For a closer review of definitions for the ‘family farm’ (See Garner and de la O Campos (2014) have reviewed 36 definitions of the term “family farm,”

2.

O’Neill and Hanrahan (2016) estimate that the average capitalisation of direct payments is approximately 21 per cent for cattle farms, 41 per cent for dairy and 50 per cent for tillage farms. On sheep farms, the capitalization is not statistically significant but the average capitalization is 35 per cent.

Appendix

Appendix A: A Description of Soil Categories

Table A1

Description of Soil Categories

Soil Category	Description
Good Soils (Classes 1 and 2)	Soils of wide use range have no limitations which cannot be overcome by normal management practices or
	Moderately wide use-range refers to soils with minor limitations such as coarse texture, moderately high altitude, less favourable climatic conditions, somewhat shallow depth, hummocky topography and somewhat weak structure.
Medium Soils (Classes 3 and 4)	The somewhat limited use range category is used for soils with similar limitations to those of Class 2 but these are present to a greater degree. For example, soils with altitude limitations in this category usually occur between 150 m and 365 m, whereas those of the moderately wide use range with altitude limitations are at elevations mostly between 90 and 150 m
	Soils in this category- are generally unsuited to tillage but suited to a permanent grassland system. The predominant limitation is poor drainage
Poor Soils	This class contains those soils whose agricultural potential is greatly restricted. They are widespread in the western and north-western regions, particularly in the mountain zones where high altitude and steep slopes are major limitations.

Source: Teagasc National Farm Survey

Appendix B: Information on the number of Land Rental Transactions

Figure A1

Download asset Open asset

Total Number of Agricultural Land Rental Transactions in Ireland Qualifying for Relief from Rental Income. Source: Revenue (2021)

Appendix C: The Relationship between Farm Size and Reliance on Family Labour

Figure A2

Download asset Open asset

Share of Family Labour in Total Labour by Farm Size (Ha.). Source: Authors calculations using Teagasc National Farm Survey 2017**Tillage farms excluded

Appendix D: Model Assumptions

Table A2

Assumptions of the ABM and Equilibrium Models

	ABM model	Equilibrium Model
Time	Transactions take place under an iterative sequential process	Transactions occurring instantly at an equilibrium price
Price Determination	Bilateral negotiation between landowner and potential tenant with reference to prevailing rental prices	Rental prices are determined solely by aggregate supply and aggregate demand
Capitalisation of Direct Payments	50 per cent of the value of direct payments are added to each bid and each reservation price	50 per cent of the value of direct payments are added to each bid and each reservation price
Reservation prices	The landowner makes decisions with reference to a reservation price, below which the landowner will not release land to the market	The landowner makes decisions with reference to a reservation price, below which the landowner will not release land to the market
Farming System	Assumed that farms remain in their current farming system.	Assumed that farms remain in their current farming system.
Farm Size Limits	Limits on farm size growth can be enforced by a central authority at the regional or national level.	No assumptions to restrict farm size growth
Rental Share	The land rental market comes to a close when the land rental share in the region reaches 30 per cent. This prevents farm exits from occuring.	No assumptions around rental share and farm exits may occur
Bid Values	The recent history of farm profitability is used to form predictions about future profitability and these predictions underline the bids and reservation prices for particular land parcels.	The recent history of farm profitability is used to form predictions about future profitability and these predictions underline the bids and reservation prices for particular land parcels.
Costs of Scale	Decreasing returns to scale - Farmers who expand beyond a certain threshold are assumed to encounter additional costs associated with the purchase of new machinery, livestock and buildings.	Constant returns to scale
Initial State	We do not assume that the initial state of the land market is perfectly competitive.
Land Tenure	Assume rented and owned land are farmed to the same profitability	Assume rented and owned land are farmed to the same profitability
Intermediary	Assumed that a market agent mediates between the land owner and tenant in negotiating each individual transaction	Walrasian auctioneer

Appendix E: Price Determination in the Microsimulation Model

The question of price determination in the ABM model is not given priority in this paper. However, there is some scope to explore this question in future research. In determining the rental price for each $z$ parcel, it can be assumed that a market agent mediates between the land owner and tenant and seeks to identify a mutually beneficial price with reference to the typical price of existing land rental agreements in the market. One does not need to make specific assumptions about whether the agent acts on behalf of the landowner or the potential tenant.

Similar to the AgriPoliS model outlined in Happe et al. (2006), one can establish the rental price for each parcel in the context of the existing regional rental rates. This allows for some smoothing and variability in the land rental price between each $z$ parcel of land.

P_{z} = \sqrt{\frac{{R E S}_{i z} + {B I D}_{j z}}{2} * R P}

where $P_{z}$ refers to the land rental price for parcel z, $RES_{iz}$ refers to the reservation price of the landowner $i$ , $BID_{jz}$ refers to the maximum willingness to pay of the highest potential bidder $j$ . RP refers to the median land rental price per hectare in each regional market. It is assumed that all transactions take place in a short period of time.

Appendix F: Price Pseudo-Code [Source code is in bold]

Merge Farm Level data for 2015 to 2017

Establish Regional Markets Based on Regional Location and Soil Quality

Regional Markets based on three locations and two soil quality variables

Calculate the following values for each farm in 2017:

Decoupled Subsidies i.e. subsidies not linked to production
Coupled Subsidies i.e. subsidies linked to production

Estimate the Value of the Bids and Reservation Prices

Farm Gross Margin minus Variable Overheads minus Subsidies
Above values are based on averages of 2015, 2016 and 2017
Add Subsidies using the values for 2017 – Assume 50% capitalisation of these subsidies into each reservation price (willingness to accept) and demand(willingness to pay)

Keep only the 2017 data

Place limits on the value of bids and reservation prices

Top Code Bids at 1,000 euro per hectare
Minimum Reservation Price 50 euro per hectare excl. decoupled payments

Establish Initial Size of Each Regional Market using the following code

egen groupsize1 = sum(group==1)
egen groupsize2 = sum(group==2)

Create Variable Names for Initial Values of Land Variables

Land Rented In
Land Let Out
Farm Size (UAA)

Calculate Initial Farm Size Concentration and Inequality in each Region using this stata code.

concindc farm_size [aw=weight], welf(farm_size)
qui gen ini_gini=r(concindex)

Begin the simulation in a loop

**Choose the Number of Runs – 1,000 is sufficient for this exercise

local runs=1000

local j= 1

while `j'<= `runs' {

Rank the farms according to the size of bids and reservation prices. Only include farms within the size limits using the following source code in Stata.

by group: egen firstrnk = rank(bid) if simland > 12 & simland <= 118 & simTILLAGEland <= 198

**********************************************************************************

Identify the highest bidder and the lowest reservation price. The first rank is the farm with the lowest profitability in the market. The highest rank number is the farm with the highest bid.

Create two separate variables for the ranking of demands and reservation prices.

The variable rnkD refers to the rank among those farms with a demand for rented land.
The variable rnkS refers to the rank among those farms with a willingness to supply rented land.

Simulate a land transfer by deducting two hectares from the landowner supplying land ie. the farm with the lowest reservation price still in the market. Add two hectares to the farm renting-in additional land using the following stata code. Similar code can be used to update the amount of land rented on each farm.

capture drop landchanged
gen landchanged = 0
replace landchanged = min(2,simlandrnd1-2) if rnkS == 1
capture drop landtransfer
sort group
by group:egen landtransfer = sum(landchanged)

replace simland = simland+landtransfer if rnkD == groupsizenew & groupsizenew != 0 replace simland = simland-landtransfer if rnkS == 1

**************************************************************************************

Include a rule that any farm expanding by 20 hectares or more incurs a reduction in the value of their bids. This may affect the ranking of the bids for the next parcel of land. The previously highest ranked farm may no longer be the highest bid for the next parcel of land. The stata code is part of a loop and facilitates the re-ranking of farms according to the size of the bid.

After each transaction, the model checks if any farm has reached the minimum or maximum limits

The code is enabled to remove a farm from the market when it reaches a size limit.

The rental share for the whole region is calculated after each transaction. In the Teagasc NFS data, this includes the weight variable uaa_weight. In this source code, the simrentin variable represents the amount of land rented by each farm. The simland variable represents the total amount of land on each farm.

References

1
The Case for Long-Term Land Leasing: A Review of the Empirical Literature
(2021)
Land 10:238.
https://doi.org/10.3390/land10030238
- Google Scholar
2
Predator or prey? Effects of farm growth on neighbouring farms
1. F Appel
2. A Balmann
(2022)
Journal of Agricultural Economics pp. 1–23.
https://doi.org/10.1111/1477-9552.12503
- Google Scholar
3
Outstanding in the Field: Evaluating Auction Markets for Farmland Using Multi-Agent Simulation
(1997)
Journal of Artificial Societies and Social Simulation 15:11.
https://doi.org/10.18564/jasss.1827
- Google Scholar
4
Farm-based modelling of regional structural change: A cellular automata approach
1. A Balmann
(1997)
European Review of Agricultural Economics 24:85–108.
https://doi.org/10.1093/erae/24.1.85
- Google Scholar
5
Market Power in Agricultural Land Markets: Concepts and Empirical Challenges
1. A Balmann
2. M Graubner
3. D Müller
4. S Hüttel
5. S Seifert
6. M Odening
7. J Plogmann
8. M Ritter
(2021)
German Journal of Agricultural Economics 70:213–235.
https://doi.org/10.30430/gjae.2021.0117
- Google Scholar
6
Agent-based spatial models applied to agriculture: a simulation tool for technology diffusion, resource use changes and policy analysis
1. T Berger
(2001)
Agricultural Economics 25:245–260.
https://doi.org/10.1111/j.1574-0862.2001.tb00205.x
- Google Scholar
7
Agent-based Modelling of Climate Adaptation and Mitigation Options in Agriculture
1. T Berger
2. C Troost
(2014)
Journal of Agricultural Economics 65:323–348.
https://doi.org/10.1111/1477-9552.12045
- Google Scholar
8
Simulating agricultural land rental markets by combining agent-based models with traditional economics concepts: The case of the Argentine Pampas
1. F Bert
2. M North
3. S Rovere
4. E Tatara
5. C Macal
6. G Podestá
(2015)
Environmental Modelling & Software 71:97–110.
https://doi.org/10.1016/j.envsoft.2015.05.005
- Google Scholar
9
Land policy in France and its consequence for the farmers
1. JP Boinon
(2012)
Agricultural Economics (Zemědělská EKONOMIKA) 49:166–172.
https://doi.org/10.17221/5374-AGRICECON
- Google Scholar
10
The factors influencing the profitability of leased land on dairy farms in Ireland
(2020)
Land Use Policy 95:104649.
https://doi.org/10.1016/j.landusepol.2020.104649
- Google Scholar
11
An agent-based approach to modeling impacts of agricultural policy on land use, biodiversity and ecosystem services
(2012)
Landscape Ecology 27:1363–1381.
https://doi.org/10.1007/s10980-012-9787-3
- Google Scholar
12
Teagasc National Farm Survey 2020 Sustainability Report
1. C Buckley
2. T Donnellan
(2021)
Galway, Ireland: Athenry, Co.
- Google Scholar
13
Female successors in Irish family farming: four pathways to farm transfer
1. A Cassidy
(2019)
Canadian Journal of Development Studies / Revue Canadienne D’études Du Développement 40:238–253.
https://doi.org/10.1080/02255189.2018.1517643
- Google Scholar
14
Land Market Imperfections and Agricultural Policy Impacts in the New EU Member States: A Partial Equilibrium Analysis
1. P Ciaian
2. JFM Swinnen
(2006)
American Journal of Agricultural Economics 88:799–815.
https://doi.org/10.1111/j.1467-8276.2006.00899.x
- Google Scholar
15
Land leasing: Findings of a study in the west region of the Republic of Ireland
1. AG Conway
(1986)
Irish Journal of Agricultural Economics and Rural Sociology 11:1–18.
- Google Scholar
16
Farmers Don’t Retire’: Re-Evaluating How We Engage with and Understand the ‘Older’ Farmer’s Perspective
(2022)
Sustainability 14:2533.
https://doi.org/10.3390/su14052533
- Google Scholar
17
Uncovering obstacles: The exercise of symbolic power in the complex arena of intergenerational family farm transfer
(2017)
Journal of Rural Studies 54:60–75.
https://doi.org/10.1016/j.jrurstud.2017.06.007
- Google Scholar
18
Going against the grain: Unravelling the habitus of older farmers to help facilitate generational renewal in agriculture
(2021)
Sociologia Ruralis 61:602–622.
https://doi.org/10.1111/soru.12355
- Google Scholar
19
Market Power in a GIS-Based Hedonic Price Model of Local Farmland Markets
(2008)
Land Economics 84:573–592.
https://doi.org/10.3368/le.84.4.573
- Google Scholar
20
Census of Agriculture 2020 - Preliminary Results
1. CSO
(2022)
21
Investors’ impact on Czech farmland prices: a microstructural analysis
(2021)
European Review of Agricultural Economics 48:97–157.
https://doi.org/10.1093/erae/jbaa029
- Google Scholar
22
Teagasc National Farm Survey 2021 Preliminary Results, Agricultural Economics and Farm Surveys Department, Rural Economy Development Programme, Teagasc
1. E Dillon
2. T Donnellan
3. B Moran
4. J Lennon
(2022)
23
Retirement farming or sustainable growth – land transfer choices for farmers without a successor
(2017)
Land Use Policy 61:526–535.
https://doi.org/10.1016/j.landusepol.2016.12.007
- Google Scholar
24
Computer Simulation Validation. Simulation Foundations, Methods and Applications
(2019)
Validation of Agent-Based Models in Economics and Finance, Computer Simulation Validation. Simulation Foundations, Methods and Applications, Springer, Cham.
- Google Scholar
25
Agent-based urban land markets: agent’s pricing behavior, land prices and urban land use change
(2009)
Journal of Artificial Societies and Social Simulation 12:3.
- Google Scholar
26
An Agent-Based Simulation Model of Structural Change in Canadian Prairie Agriculture, 1960-2000
(2009)
Canadian Journal of Agricultural Economics/Revue Canadienne d’agroeconomie 57:537–554.
https://doi.org/10.1111/j.1744-7976.2009.01169.x
- Google Scholar
27
Identifying the Family Farm. An Informal Discussion of the Concepts and Definitions
1. E Garner
2. AP de la O Campos
(2014)
Food and Agriculture Organization of the United Nations, Agricultural Development Economics Division (ESA.
- Google Scholar
28
The effect of farmer attitudes on openness to land transactions: evidence for Ireland
(2021)
Bio-Based and Applied Economics 10:153–168.
https://doi.org/10.36253/bae-9746
- Google Scholar
29
Agent-based Models
1. N Gilbert
(2007)
Quantitative Applications in the Social Sciences 153:112.
- Google Scholar
30
Measurement of Inequality of Incomes
1. C Gini
(1921)
The Economic Journal 31:124.
https://doi.org/10.2307/2223319
- Google Scholar
31
Lost in space? The effect of direct payments on land rental prices
1. M Graubner
(2018)
European Review of Agricultural Economics 45:143–171.
https://doi.org/10.1093/erae/jbx027
- Google Scholar
32
A standard protocol for describing individual-based and agent-based models
1. V Grimm
2. U Berger
3. F Bastiansen
4. S Eliassen
5. V Ginot
6. J Giske
7. J Goss-Custard
8. T Grand
9. SK Heinz
10. G Huse
11. A Huth
12. JU Jepsen
13. C Jørgensen
14. WM Mooij
15. B Müller
16. G Pe’er
17. C Piou
18. SF Railsback
19. AM Robbins
20. MM Robbins
21. E Rossmanith
22. N Rüger
23. E Strand
24. S Souissi
25. RA Stillman
26. R Vabø
27. U Visser
28. DL DeAngelis
(2006)
Ecological Modelling 198:115–126.
https://doi.org/10.1016/j.ecolmodel.2006.04.023
- Google Scholar
33
The ODD protocol: A review and first update
1. V Grimm
2. U Berger
3. DL DeAngelis
4. JG Polhill
5. J Giske
6. SF Railsback
(2010)
Ecological Modelling 221:2760–2768.
https://doi.org/10.1016/j.ecolmodel.2010.08.019
- Google Scholar
34
Agent-based Analysis of Agricultural Policies: an Illustration of the Agricultural Policy Simulator AgriPoliS, its Adaptation and Behavior
(2006)
Ecology and Society 11:49.
https://doi.org/10.5751/ES-01741-110149
- Google Scholar
35
The Inefficiencies of Regionalised Milk Quota Trade
(2009)
Journal of Agricultural Economics 60:334–347.
https://doi.org/10.1111/j.1477-9552.2008.00187.x
- Google Scholar
36
The Happy Farmer: The Effect of Nonpecuniary Benefits on Behavior
1. P Howley
(2015)
American Journal of Agricultural Economics 97:1072–1086.
https://doi.org/10.1093/ajae/aav020
- Google Scholar
37
Explaining the economic ‘irrationality’ of farmers’ land use behaviour: The role of productivist attitudes and non-pecuniary benefits
(2015)
Ecological Economics 109:186–193.
https://doi.org/10.1016/j.ecolecon.2014.11.015
- Google Scholar
38
Handbook of Income Distribution
1. M Jäntti
2. SP Jenkins
(2015)
807–935, Income mobility, Handbook of Income Distribution, Vol, 2, Elsevier, p.
- Google Scholar
39
Trends in income inequality, pro-poor income growth, and income mobility
1. SP Jenkins
2. P Van Kerm
(2009)
Oxford Economic Papers 58:531–548.
https://doi.org/10.1093/oep/gpl014
- Google Scholar
40
Farm Succession in Modern Ireland: Elements of a Theory of Inheritance
1. L Kennedy
(1991)
The Economic History Review 44:477.
https://doi.org/10.2307/2597540
- Google Scholar
41
A review of Agent Based Modeling for agricultural policy evaluation
(2018)
Agricultural Systems 164:95–106.
https://doi.org/10.1016/j.agsy.2018.03.010
- Google Scholar
42
Policy drivers of farm succession and inheritance
(2017)
Land Use Policy 61:147–159.
https://doi.org/10.1016/j.landusepol.2016.09.006
- Google Scholar
43
Alternative measures of Family Farm Viability – Incorporating gap measures
(2022)
Journal of Rural Studies 89:257–274.
https://doi.org/10.1016/j.jrurstud.2021.11.022
- Google Scholar
44
A Microsimulation Model for Risk in Irish Tillage Farming
(2016)
International Journal of Microsimulation 9:41–76.
https://doi.org/10.34196/ijm.00135
- Google Scholar
45
Inequality and Concentration in Farmland Size: A Regional Analysis for Western Europe
1. J Loughrey
2. T Donnellan
(2017)
The XV EAAE Congress, “Towards Sustainable Agri-food Systems: Balancing Between Markets and Society.
- Google Scholar
46
The Agricultural Land Market in the EU and the Case for Better Data Provision
(2020)
EuroChoices 19:41–47.
https://doi.org/10.1111/1746-692X.12212
- Google Scholar
47
The Measurement of Average Farm Size
1. P Lund
2. R Price
(1998)
Journal of Agricultural Economics 49:100–110.
https://doi.org/10.1111/j.1477-9552.1998.tb01254.x
- Google Scholar
48
The Code is the Model
1. L Meisser
(2017)
International Journal of Microsimulation 10:184–201.
https://doi.org/10.34196/ijm.00169
- Google Scholar
49
Spatial Microsimulation for Rural Policy Analysis
1. C O’Donoghue
(2013)
177–191, Modelling farm viability, Spatial Microsimulation for Rural Policy Analysis, Berlin, Heidelberg, Springer, p.
- Google Scholar
50
Farm-Level Microsimulation Modelling
1. C O’Donoghue
(2017)
147–175, Spatial Microsimulation of Farm Income, Farm-Level Microsimulation Modelling, Cham, Palgrave Macmillan, p.
- Google Scholar
51
The capitalization of coupled and decoupled CAP payments into land rental rates
1. S O’Neill
2. K Hanrahan
(2016)
Agricultural Economics 47:285–294.
https://doi.org/10.1111/agec.12229
- Google Scholar
52
Spatial Effects within the Agricultural Land Market in Northern Ireland
1. M Patton
2. S McErlean
(2003)
Journal of Agricultural Economics 54:35–54.
https://doi.org/10.1111/j.1477-9552.2003.tb00047.x
- Google Scholar
53
How do agricultural policies influence farm size inequality? The example of France
(2012)
European Review of Agricultural Economics 39:5–28.
https://doi.org/10.1093/erae/jbr035
- Google Scholar
54
What drives competition on the farmland market? A case study in Brittany (France)
1. L Piet
2. R Melot
3. S Diop
(2021)
European Review of Agricultural Economics 48:60–96.
https://doi.org/10.1093/erae/jbaa019
- Google Scholar
55
Social Simulation: Technologies, Advances and New Discoveries
(2008)
81–97, Effects of land markets on competition between innovators and imitators in land use: results from FEARLUS-ELMM, Social Simulation: Technologies, Advances and New Discoveries, IGI Global, p.
- Google Scholar
56
Analysis of environmental and economic efficiency using a farm population micro-simulation model
(2011)
Mathematics and Computers in Simulation 81:1344–1352.
https://doi.org/10.1016/j.matcom.2010.04.018
- Google Scholar
57
On the development and use of farm models for policy impact assessment in the European Union – A review
(2018)
Agricultural Systems 159:111–125.
https://doi.org/10.1016/j.agsy.2017.10.012
- Google Scholar
58
The Farming Sector in Ireland: A Profile from Revenue Data
1. Revenue
(2021)
59
Developing farm-level sustainability indicators for Ireland using the Teagasc National Farm Survey
1. M Ryan
2. T Hennessy
3. C Buckley
4. EJ Dillon
5. T Donnellan
6. K Hanrahan
7. B Moran
(2016)
Irish Journal of Agricultural and Food Research 55:112–125.
https://doi.org/10.1515/ijafr-2016-0011
- Google Scholar
60
Teagasc Beef Manual – Infrastructure - Winter accommodation for beef animals
1. T Ryan
2. JJ Lenehan
(2016)
61
Agent-Based Modelling of Social-Ecological Systems: Achievements, Challenges, and a Way Forward
(2017)
Journal of Artificial Societies and Social Simulation 20:1–27.
https://doi.org/10.18564/jasss.3423
- Google Scholar
62
SCSI/Teagasc Agricultural Land Market Review and Outlook 2022, Dublin, Ireland
1. SCSI/Teagasc
(2022)
63
Direct Payments, Spatial Competition, and Farm Survival in Norway
(2015)
American Journal of Agricultural Economics 97:1192–1205.
https://doi.org/10.1093/ajae/aau085
- Google Scholar
64
The Diversity of Land Markets and Regulations in Europe, and (some of) its Causes
(2016)
The Journal of Development Studies 52:186–205.
https://doi.org/10.1080/00220388.2015.1060318
- Google Scholar
65
Dairy Farm Infrastructure Handbook
1. Teagasc
(2017)
66
Land concentration and land grabbing in Europe: a preliminary analysis
(2015)
Canadian Journal of Development Studies / Revue Canadienne D’études Du Développement 36:147–162.
https://doi.org/10.1080/02255189.2015.1027673
- Google Scholar
67
Farm/Household-Level Simulation Results of Testing Policy and Other Scenarios
1. D Viaggi
2. F Bartolini
3. M Puddu
4. M Raggi
(2013)
Factor Markets Working Paper No: 54.
- Google Scholar

Article and author information

Author details

Jason Loughrey

Teagasc Rural Economy and Development Programme, Galway, Ireland

For correspondence
jason.loughrey@teagasc.ie

"This ORCID iD identifies the author of this article:" 0000-0001-9658-0801
Thia Hennessy

Cork University Business School, Cork, Ireland

"This ORCID iD identifies the author of this article:" 0000-0002-6137-1249

Funding

The authors acknowledge the funding support of the Department of Agriculture, Food and the Marine under the project entitled ‘Analysis of the Functioning of Irish Agricultural Land Markets’.

Acknowledgements

The authors are grateful to Professor Matteo Richiardi and the two anonymous reviewers for detailed and constructive comments on our original submission to the International Journal of Microsimulation.The authors are grateful to participants from the EAAE Seminar ‘Agricultural Land Markets – Recent Developments, Efficiency and Regulation’ held in Berlin in April 2019 and participants from the 7th World Congress of the International Microsimulation Association held in NUI Galway in June 2019 for their valuable questions, comments and suggestions.

Publication history

Version of Record published: August 31, 2022 (version 1)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Download citations (links to download the citations from this article in formats compatible with various reference manager tools)

BibTeX
RIS

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Description of the Agent-Based Model of the Agricultural Land Market

Summary Statistics for Six Regional Markets

Rental Price Statistics for Six Regional Markets

Simulated Average Farm Size by System

Simulated Share of Agricultural Land by System

Change in Average Farm Size by System 2017 to 2020

Total Agricultural Area by Farming System 2010-2020

Farm Size Inequality by Group under Profit Maximisation

Mid-Point Hectare Statistic by Group under Profit Maximisation

Progressivity or Regressivity of Distribution in Post-Simulation

Market for Good Agricultural Land in South-West and Mid-West Region

Market for Good Agricultural Land in East Region

Market for Good Agricultural Land in BMW Region

Description of Soil Categories

Total Number of Agricultural Land Rental Transactions in Ireland Qualifying for Relief from Rental Income. Source: Revenue (2021)

Share of Family Labour in Total Labour by Farm Size (Ha.). Source: Authors calculations using Teagasc National Farm Survey 2017**Tillage farms excluded

Assumptions of the ABM and Equilibrium Models

Author details

Jason Loughrey

For correspondence

Thia Hennessy

Downloads (link to download the article as PDF)

Download citations (links to download the citations from this article in formats compatible with various reference manager tools)

Open citations (links to open the citations from this article in various online reference manager services)

Categories and tags